考慮服務技能約束的家政服務雙邊穩定匹配方法

孔德財，劉長平，崔杰

（1.淮陰工學院管理工程學院，江蘇淮安 223003；2.江蘇省智能工廠工程研究中心，江蘇淮安 223003）

0 引言

隨著經濟社會的發展以及城市生活和工作節奏的加快，居民對家政服務呈多樣性需求；與此同時，農村人口不斷涌入城市，大學畢業生逐年增加，在加劇就業壓力的同時也在一定程度上擴大了家政服務人員的規模，由此促進了我國家政服務行業的迅猛發展［1-2］。然而，長期制約家政服務行業蓬勃發展的重要問題之一是，即便雇主給出高工資有時也難以雇到合適的家政服務人員，而家政服務人員也經常因難以找到滿意工作而苦惱，具體體現在雇主的高解雇率和家政服務人員的高辭職率［3］。雇主和家政服務人員間無法實現相對穩定的匹配狀態，是造成當前家政服務市場混亂無序的重要原因之一。因此，考慮雇主和家政服務人員的雙方需求，獲得雙方穩定匹配，降低搜尋成本，提高匹配滿意度，對于維護家政服務市場秩序，促進家政服務行業的健康發展具有重要的現實意義。

GALE 等［4］在研究男女婚戀匹配和大學錄取問題時，首次提出穩定匹配概念，并給出了獲得穩定匹配的延遲接受算法。ROTH［5］采用實證研究方法，對比了英國國民健康服務（NHS）在不同地區的實習生招聘制度，證實了穩定匹配機制的重要性。SHAPLEY 和ROTH 因在穩定匹配理論及機制設計實踐方面的貢獻，被授予2012 年諾貝爾經濟學獎。關于穩定匹配理論的研究和應用目前已從男女婚戀匹配、大學錄取、醫院和實習生匹配［6-9］等傳統匹配市場擴展至其他服務行業。BARRON 等［10］針對國際貨幣基金組織中的人員與部門匹配機制缺陷，提出了采用基于延遲接受算法的集中化穩定匹配機制。KORKMAZ 等［11］為解決軍隊中人員類型與崗位匹配問題，構建了基于層次分析法和穩定匹配算法的決策支持系統。GHAROTE 等［12］采用集中化穩定匹配機制研究了實習生與軟件項目需求間的匹配問題，針對軟件項目需求具有任意長度無差異偏好列表的特點，建立了再培訓和重新安置成本最小化的優化模型，并設計了基于GRASP 的散射搜索算法求解大規模問題。PENG 等［13］針對干散貨航運市場中船舶與貨物之間的匹配問題，構建了以船貨總體效用最大為目標的優化穩定匹配模型，開發了基于Gale-Shapley 算法的價格博弈機制，研究由托運人主導的市場、由承運人主導的市場和均衡市場3 種情景，結果表明，如果弱勢參與者以價格博弈機制出價，即使他們處于劣勢也可能獲得更多收益。袁鐸寧等［14］針對手術醫生和擇期手術患者的一對多雙邊匹配問題，構建了滿足期望水平的醫患穩定匹配方案的多目標優化模型。李銘洋等［15］針對具有屬性期望的多屬性雙邊匹配問題，依據行為決策理論中的失望理論，構建了以雙方主體感知效用最大化為目標的多目標穩定匹配模型。

雖然關于穩定匹配理論的研究取得了一些成果，有些甚至已被應用于現實生活［16-19］，但目前尚未見關于家政服務人員和雇主的穩定匹配研究。因此，關于家政服務人員和雇主的穩定匹配研究具有一定的理論意義和實際應用價值。基于此，筆者在已有穩定匹配理論基礎上，提出一種考慮服務技能約束的家政服務雙邊穩定匹配方法。

1 問題描述

用HSM(a，b，c，d)表示家政服務人員與雇主的雙邊匹配問題，其中，a表示一名家政服務人員可以匹配的雇主最大數量；b表示雇主需要的家政服務人員最大數量；c表示家政服務人員擁有的家政服務技能數量；d表示雇主需要的家政服務技能數量。本文研究HSM(1，1，n，1)，即一名家政服務人員最多可以為一名雇主服務，一名雇主只雇傭一名家政服務人員，家政服務人員擁有多項服務技能而每名雇主只需要一項服務技能。

設W={W1，W2，…，Wm}為m名家政服務人員組成的集合，其中Wi代表第i名家政服務人員，i=1，2，…，m；E={E1，E2，…，En}為n名雇主組成的集合，其中Ej代表第j名雇主，j=1，2，…，n。在雇主雇傭家政服務人員時，家政服務人員擁有的服務技能只有在滿足雇主需要的服務技能時，二者才可能實現最終匹配，因此，需考慮技能匹配約束。設S={S1，S2，…，Sl}為家政服務技能集合，其中Sk代表第k項服務技能，k=1，2，…，l。家政服務人員具備的技能記為矩陣P=[pik]m×l，其中pik=0 或1。pik=0 表示家政服務人員Wi不具備第k項技能；pik=1 表示家政服務人員Wi具備第k項技能，i=1，2，…，m，k=1，2，…，l。雇主需要的服務技能記為矩陣Q=[qjk]n×l，其中qjk=0 或1。qjk=0 表示雇主Ej不需要第k項服務技能，qjk=1 表示雇主Ej需要第k項服務技能，j=1，2，…，n，k=1，2，…，l。

在家政服務人員與雇主的雙邊匹配問題中，雇主不僅對家政服務人員的服務技能有要求，還會依據家政服務人員的性別、年齡、工作經驗等進行總體評價，并對家政服務人員進行偏好排序。同樣，家政服務人員在選擇雇主時也會考慮工資待遇、工作環境、工作地點等，并進行相應的雇主偏好排序。家政服務人員Wi對雇主Ej的偏好排序記為矩陣R=[rij]m×n，i=1，2，…，m，j=1，2，…，n，其中rij∈{1，2，…，n+1}，若rij∈{1，2，…，n}，則表示家政服務人員Wi將Ej排在第rij位；若rij=n+1，則表示對家政服務人員Wi而言，雇主Ej是不可接受的。雇主Ej給出的家政服務人員Wi的偏好排序記為矩陣T=[tij]m×n，i=1，2，…，m，j=1，2，…，n，其中tij∈{1，2，…，m+1}，若tij∈{1，2，…，m}，則表示雇主Ej將家政服務人員Wi排在第tij位；若tij=m+1，則表示對雇主Ej而言，家政服務人員Wi是不可接受的。若家政服務人員Wi給出的雇主Ej的序值rij越小，則Wi對Ej越滿意，反之亦然；類似地，若雇主Ej給出的家政服務人員Wi的序值tij越小，則Ej對Wi越滿意，反之亦然。

下面給出偏好可接受對、技能可接受對、可行技能約束匹配、技能約束阻塞對、技能約束穩定匹配等定義。

定義1（偏好可接受對）在HSM(1，1，n，1)中，對于任意的Wi∈W，Ej∈E，若(Wi，Ej)∈W×E滿足rij≠n+1 且tij≠m+1，則稱(Wi，Ej)為偏好可接受對；否則，稱(Wi，Ej)為偏好不可接受對。

在HSM(1，1，n，1)中，若家政服務人員所具備的技能能滿足雇主需求，則稱家政服務人員和雇主為技能可接受對；否則，稱家政服務人員和雇主為技能不可接受對。

定義2（技能可接受對）在HSM(1，1，n，1)中，對于任意的Wi∈W，Ej∈E，若(Wi，Ej)∈W×E滿足=1，則稱(Wi，Ej)為技能可接受對；否則，稱(Wi，Ej)為技能不可接受對。

定義3（可行技能約束匹配）設μ是HSM(1，1，n，1)中的一對一雙邊匹配，若對于任意的(Wi，Ej)∈μ都是偏好可接受對，且均為技能可接受對，則稱匹配方案μ為可行技能約束匹配。

在匹配方案μ中，若家政服務人員Wi和雇主Ej均認為對方優于其在匹配方案μ中的匹配對象，且Wi滿足Ej的服務技能需求，則稱(Wi，Ej)是技能約束阻塞對。

定義4（技能約束阻塞對）在HSM(1，1，n，1)中，設家政服務人員與雇主的一對一雙邊匹配μ：W∪E→W∪E，在匹配方案μ中，對于任意的Wi∈W，Ej∈E，若偏好可接受對(Wi，Ej)同時滿足以下條件：

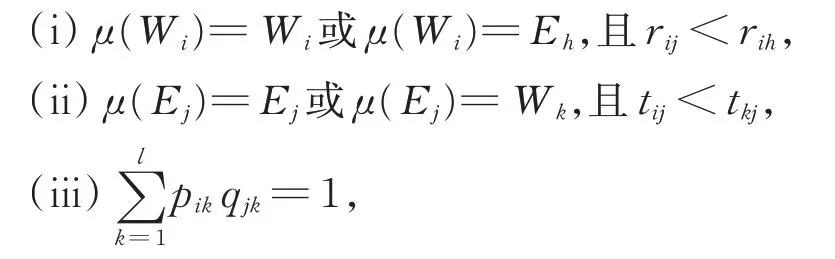
則稱(Wi，Ej)是匹配方案μ的技能約束阻塞對。

定義5（技能約束穩定匹配）在HSM(1，1，n，1)中，設家政服務人員與雇主的一對一雙邊匹配μ：W∪E→W∪E，若匹配方案μ是可行技能約束匹配，且μ中不存在技能約束阻塞對，則稱匹配方案μ為技能約束穩定匹配。

本文的目的是依據家政服務人員具備的技能P=[pik]m×l和雇主需要的技能Q=[qjk]n×l，以及家政服務人員和雇主的偏好信息R=[rij]m×n和T=[tij]m×n，采用雙邊匹配決策方法，獲得雙方的最優技能約束穩定匹配方案。

2 技能約束穩定匹配決策方法

2.1 家政服務人員和雇主的滿意度計算

家政服務人員的滿意度記為矩陣A=[αij]m×n，雇主的滿意度記為矩陣B=[βij]m×n，i=1，2，…，m，j=1，2，…，n。在現實的家政服務人員與雇主的雙邊匹配過程中，由于受家政服務人員的心理行為影響，使得其對雇主的滿意度與偏好排序值之間呈非線性關系。例如，對排在第1 位的雇主滿意度可能為1，對排在第2 位的雇主滿意度為0.95，對排在第3 位的雇主滿意度為0.75，等等。類似地，雇主對家政服務人員的滿意度與偏好排序值之間也存在類似的非線性關系。因此，為更準確地刻畫家政服務人員和雇主的滿意度，給出了家政服務人員Wi對雇主Ej滿意度的計算式：

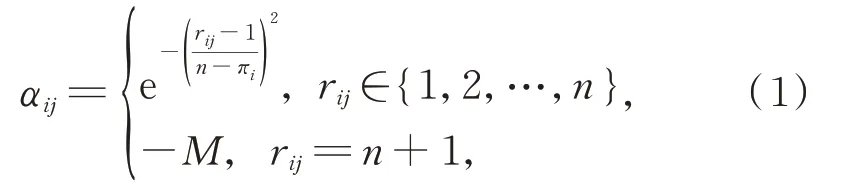
其中，M為足夠大的正數，πi表示家政服務人員Wi不可接受的雇主數量。

雇主Ej對家政服務人員Wi的滿意度計算式為

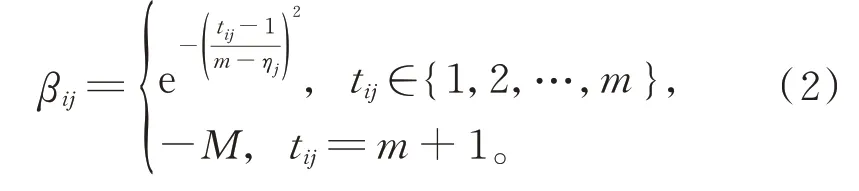
其中，ηj表示雇主Ej不可接受的家政服務人員數量。

在式（1）和式（2）中，家政服務人員和雇主的滿意度是關于序值的嚴格單調遞減非線性函數。如果家政服務人員Wi認為雇主Ej是可接受的，則0 ＜αij≤1；如果家政服務人員Wi認為雇主Ej是不可接受的，則αij=-M。雇主對家政服務人員的情況類似。

2.2 模型

依據家政服務人員的滿意度A=[αij]m×n和雇主的滿意度B=[βij]m×n，建立以家政服務人員和雇主總體滿意度最大化為目標的數學模型。設xij為0-1 型決策變量，xij=1 表示家政服務人員Wi與雇主Ej形成匹配對；否則，xij=0。進一步，可構建0-1 型雙目標整數規劃模型，見式（3）～式（11）。

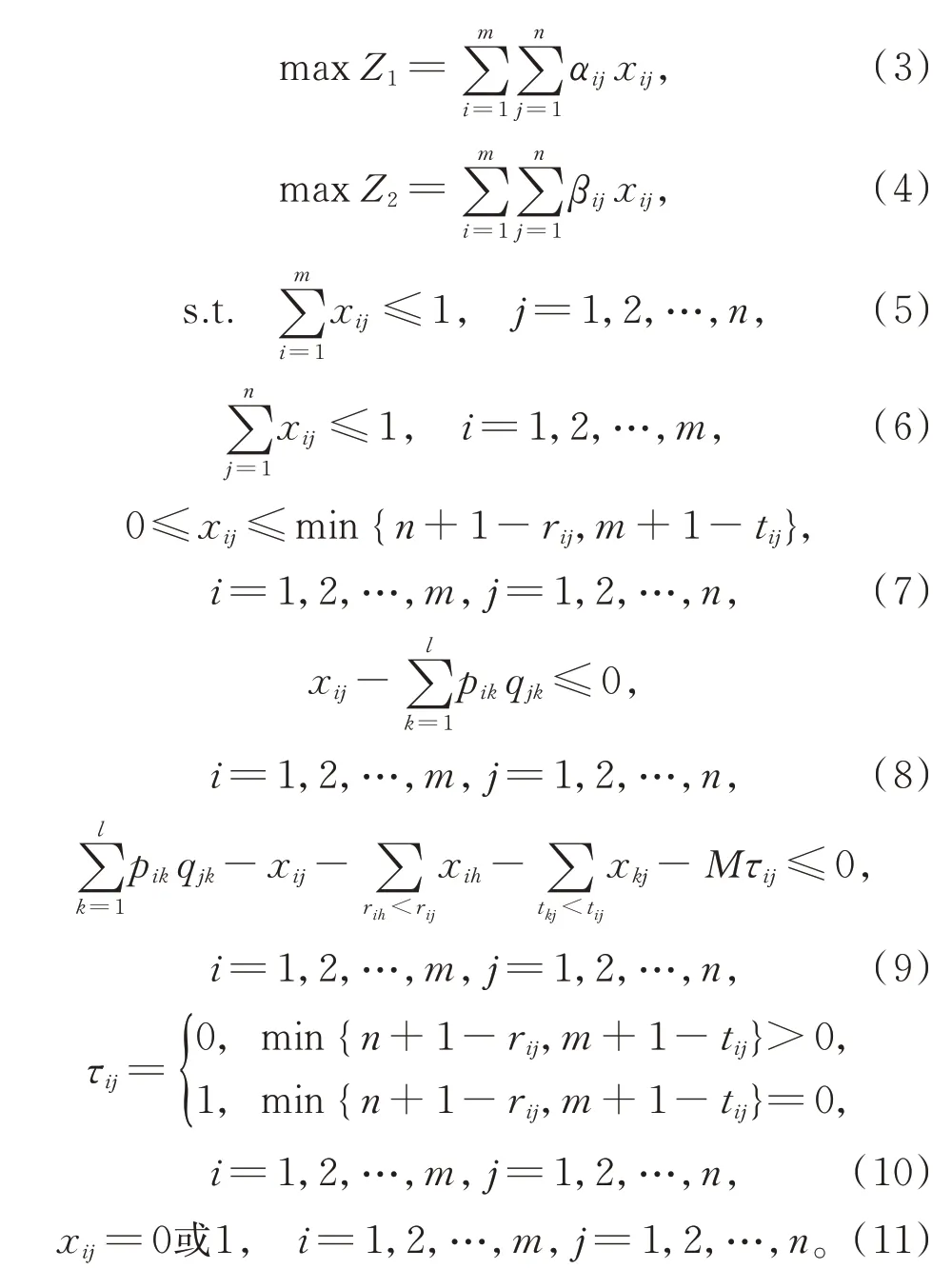
其中，式（3）和式（4）為目標函數，式（3）表示最大化家政服務人員的滿意度，式（4）表示最大化雇主的滿意度。式（5）～式（11）為約束條件，式（5）和式（6）為匹配數量約束，式（5）表示一名雇主最多需要一名家政服務人員，式（6）表示一名家政服務人員最多為一名雇主提供服務，式（7）為偏好可接受對約束，保證進行匹配的家政服務人員和雇主是偏好可接受的，式（8）為技能可接受對約束，保證在家政服務人員和雇主進行匹配時滿足服務技能約束，式（9）為技能約束穩定匹配的約束條件，其中M是足夠大的正數，式（10）保證只有可接受對才能成為技能約束穩定匹配，式（11）為決策變量取值約束。

對于任意的HSM(1，1，n，1)，設由式（3）～式（11）的可行解構成的穩定匹配集合為Ω，HSM(1，1，n，1)的所有穩定匹配構成的集合為U。

引理1在式（3）～式（11）中，任意一個可行解對應的匹配方案都是HSM(1，1，n，1)的技能約束穩定匹配，Ω?U。

證明設在式（3）～式（11）中，任意一個可行解為X=[xij]m×n，i∈{1，2，…，m}，j∈{1，2，…，n}，與可行解X對應的匹配方案為μ。將式（5）和式（6）作為匹配數量約束，以保證了家政服務人員與雇主的一對一雙邊匹配，即一名家政服務人員最多與一名雇主匹配，一名雇主最多與一名家政服務人員匹配。因此，μ是HSM(1，1，n，1)中的一對一雙邊匹配。式（7）和式（8）分別為偏好可接受對約束和技能可接受對約束，保證了μ是可行技能約束匹配。

為證明式（9）能夠保證可行技能約束匹配μ是技能約束穩定匹配，可證明滿足式（9）中的由任意的Wi∈W和Ej∈E組成的(Wi，Ej)不是技能約束阻塞對。若(Wi，Ej)是偏好不可接受對，即τij=1，則式（9）必成立，顯然(Wi，Ej)不是技能約束阻塞對。若(Wi，Ej)是技能不可接受對，即=0，則式（9）必成立，顯然(Wi，Ej)不是技能約束阻塞對。

下證若(Wi，Ej)是偏好可接受對和技能可接受對，則式（9）保證(Wi，Ej)不是技能約束阻塞對。

若(Wi，Ej)是偏好可接受對，即τij=0，則式（9）可化簡為

引理2在HSM(1，1，n，1)中，任意一個技能約束穩定匹配都是式（3）～式（11）的可行解，即U?Ω。

證明設μ是HSM(1，1，n，1)中的技能約束穩定匹配方案。對于任意的Wi∈W，Ej∈E，若(Wi，Ej)∈μ，則令xij=1；否則，令xij=0。由于μ是一對一雙邊匹配，Wi和Ej無匹配對象或最多有一個匹配對象，因此，式（5）和式（6）成立。此外，由定義5 可知，μ中的匹配對均為偏好可接受對和技能可接受對，因此，式（7）和式（8）必成立。

下證技能約束穩定匹配μ對應的模型解滿足式（9）。

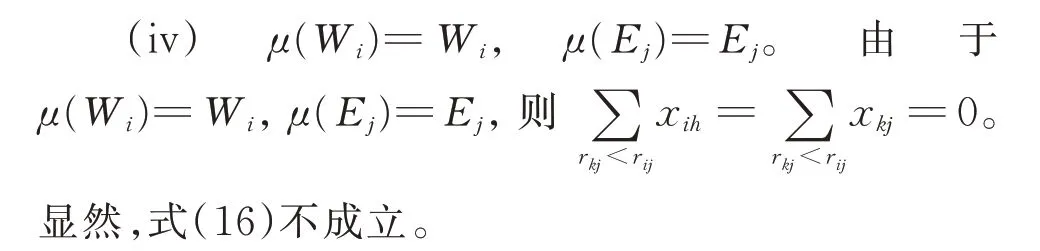
因此，在xij=0 且(Wi，Ej)是偏好可接受對和技能可接受對情形下，若(Wi，Ej)不是匹配方案μ的技能約束阻塞對，則式（9）必成立。由此可證，在技能約束匹配方案μ中，對于任意的Wi∈W，Ej∈E，均能使式（9）成立。

綜上可知，任何一個技能約束穩定匹配都是式（3）～式（11）的可行解，即U?Ω。

證畢。

由引理1 和引理2，易得

定理1對于任意給定的HSM(1，1，n，1)，均有Ω=U。

2.3 模型求解

式（3）～式（11）是雙目標的0-1 整數規劃模型，本文采用ε-約束算法求解［20?21］。其基本思想是將其中1 個目標函數轉換為約束條件，從而將雙目標優化模型轉換為單目標優化模型進行求解。

下面以目標函數Z2作為約束條件，說明ε-約束算法的具體流程。

令S為目標函數值集合，迭代步長為θ。

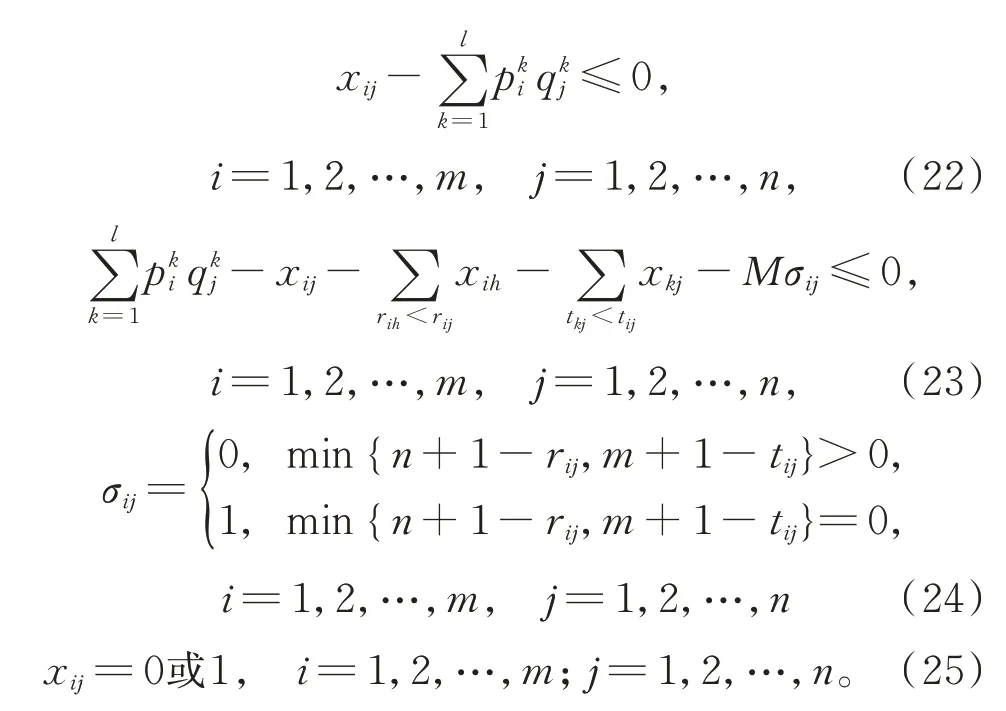
步驟5刪除S中被占優的點，獲得帕累托前沿，算法結束。

依據ε-約束算法理論，式（17）～式（25）的每個最優解都是式（3）～式（11）的帕累托解，因此，用上述算法通過不斷迭代，可獲得式（3）～式（11）的帕累托前沿。

3 算例分析

某專業、正規、服務管理體系完善的家政服務機構，可提供保姆、醫療陪護、月嫂、育嬰師、鐘點工、管家等家政服務。在一段時間內有8 名家政服務人員{W1，W2，…，W8}通過網絡平臺或中介門店尋找工作，每名家政服務人員都希望尋找一份合適的工作；有8 名雇主{E1，E2，…，E8}通過網絡平臺或中介門店尋求家政服務人員，每名雇主只雇傭一名家政服務人員。8 名家政服務人員掌握的技能包括做飯保潔、醫療陪護、月嫂、家庭護理、育嬰護理5 種，分別用S1，S2，S3，S4，S5表示，每名家政服務人員掌握其中的一項或幾項技能，8 名家政服務人員掌握的具體技能和8 名雇主需要的服務技能分別為

家政服務人員依據8 名雇主提供的工資待遇、食宿條件、工作環境等對各項指標進行總體評價并給出偏好排序值R=[rij]8×8。雇主依據8 名家政服務人員的工作經驗、年齡、技能水平等對各項指標進行總體評價并給出偏好排序值T=[tij]8×8。

由式（1）和式（2），分別得到家政服務人員和雇主的滿意度為

依據家政服務人員滿意度和雇主滿意度，建立式（3）～式（11）所示的雙目標優化模型，并采用ε-約束算法求解模型。取迭代步長θ=0.1，以目標函數Z2為約束條件進行求解：

最后，對模型進行迭代求解，得到帕累托最優解和對應的目標函數值，見表1。

表1 技能約束穩定匹配方案Table 1 Skill constraints stable matching schemas

家政服務中介機構可根據實際情況從中選擇最優穩定匹配結果。例如，若選擇家政服務人員最滿意的穩定匹配，則為方案μ1；若選擇雇主最滿意的穩定匹配，則為方案μ6；若選擇雙方滿意度差值最小的穩定匹配，則為方案μ2。

4 結論

針對家政服務行業中家政服務人員與雇主的雙邊匹配問題，提出了一種基于穩定匹配理論的雙邊匹配決策方法，主要貢獻體現在：（1）針對家政服務市場需考慮技能匹配約束的特點，給出了技能約束穩定匹配的定義；（2）給出了匹配雙方序值與滿意度的非線性計算式；（3）構建了考慮穩定性和滿意度的技能約束匹配優化模型，并證明了模型的合理性。提出的決策方法彌補了已有家政服務人員與雇主雙邊匹配中未考慮匹配穩定性不足的問題，為解決現實家政服務行業中雇主的高解雇率和家政服務人員的高辭職率問題提供了一種新方法和新途徑。