面向飛行器遙測數據的關聯規則挖掘方法研究

(中國運載火箭技術研究院，北京 100076)

0 引言

近年來數據挖掘技術得到了迅速的發展,如相似模式搜索，模式聚類，事件檢測，規則提取等技術和方法已經成功應用于金融、醫療、生物等領域[1]。隨著近年來飛行任務的不斷增加，大量飛行器的飛行試驗積累了海量遙測數據。飛行器遙測數據是地面運管系統判斷其運行狀態的唯一依據[2]，是遙測地面分析系統的最要組成部分[3]。充分利遙測數據進行對比分析，有助于故障分析和掌握飛行器的飛行特征，并不斷改進設計以提高飛行器產品的質量[4]，對于提高飛行器在軌運行的安全性和可靠性具有重要的意義[5]。而我國在航天領域的大數據挖掘還處于理論研究、探索階段。

本文針對飛行器電源系統遙測數據的關聯規則挖掘算法進行了對比分析，并以基于時間時序的飛行器電源系統遙測參數中，某幾個參數之間的關聯規則為例，進行試驗對比和數據驗證，為未來飛行器遙測參數關聯規則挖掘提供參考。

1 飛行器遙測數據特點

飛行器在地面試驗、發射、在軌飛行等階段均會產生大量的數據，數據量大是飛行器遙測數據的顯著特點。同時由于飛行器本身是個復雜的系統，遙測數據又包含電力、溫度、壓力、速度等各個方面，因此數據種類多也是飛行器遙測數據的明顯特點。在繁多的數據中，數據類型不僅限于數字、文本，圖像、視頻、音頻等數據的頻繁使用，也使數據類型的多樣性特征凸顯出來。

2 關聯規則挖掘算法

2.1 基于FP-Growth算法的關聯規則挖掘

FP-Growth(Frequent Pattern Growth)算法是一種不產生候選模式，而采用頻繁模式增長的方法挖掘頻繁模式的算法[6]。它是一種擴展的前綴樹(即FP樹)結構,存儲了關于頻繁模式數量的重要信息.樹中只包含長度為1的頻繁項作為節點,并且那些頻度高的節點更靠近樹的根節點,因此,頻度高的項比那些頻度低的項有更多的機會共享同一個節點[7]?；谶@一特性，可以計算出各頻繁項間的關聯規則。

基于FP-Growth算法的關聯規則挖掘分為構建FP樹，利用FP樹挖掘頻繁項集，關聯規則挖掘3個步驟。以飛行器供電系統中電壓與系統指令的遙測數據為例，電壓值的變化與發出的指令密切相關，假設由電壓A,B,C和指令D,E構成示例數據集，如表1所示。其中第一條數據{A,B}表示電壓A與B在時刻1時發生變化，而第四條數據{A,B,C,E}表示電壓A,B,C在時刻4時發生變化，同時指令E發出。

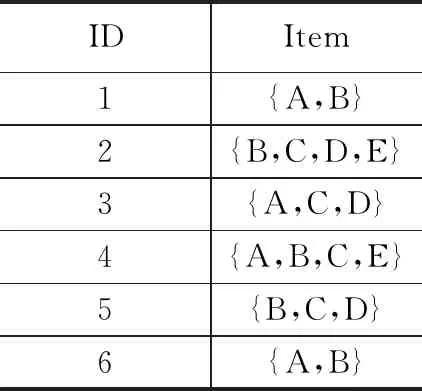
表1 示例數據集

1)構建FP樹:

掃描示例數據集(表1)中全部數據，計算出頻繁項集F1。設定最小支持度為2，如果任何一個頻繁項的頻繁度小于等于最小支持度，則將該頻繁項從頻繁項集中刪除。在頻繁項集F1中，頻繁項“E”的頻繁度為2，則從頻繁項集F1中刪除頻繁項“E”。然后將頻繁項集F1按照頻繁度降序排序，得出表2所示結果。

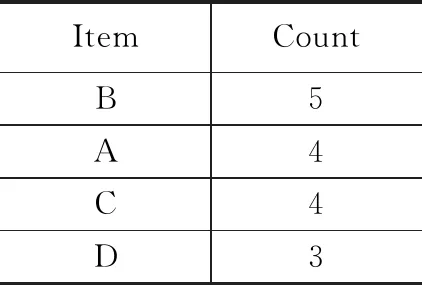
表2 頻繁項集F1

將示例數據集中全部數據按照頻繁項集F1中的記錄重新排序，如表3所示。

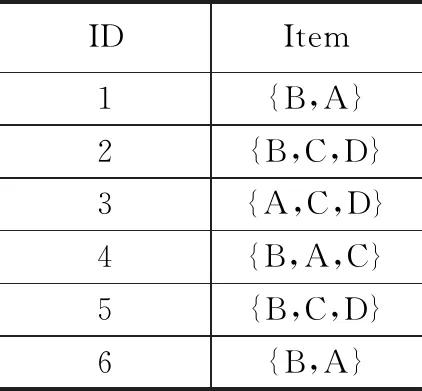
表3 排序后的數據

建立FP樹根節點“root”,從根節點出發，第一條數據{B,A}各頻繁項“B”和“A”按照順序依次加入FP樹中，并記錄各節點頻數Count為1；當第二條數據{B,C,D}加入FP樹時，首個頻繁項“B”已經在FP樹中存在，則只需將“B”節點的頻數Count加1，然后再將頻繁項“C”作為節點“B”的一個新子節點加入FP樹中從而得到一個新的分支。如此往復，將表3中每條數據依次加入到FP樹中，得到圖1所示的FP樹。

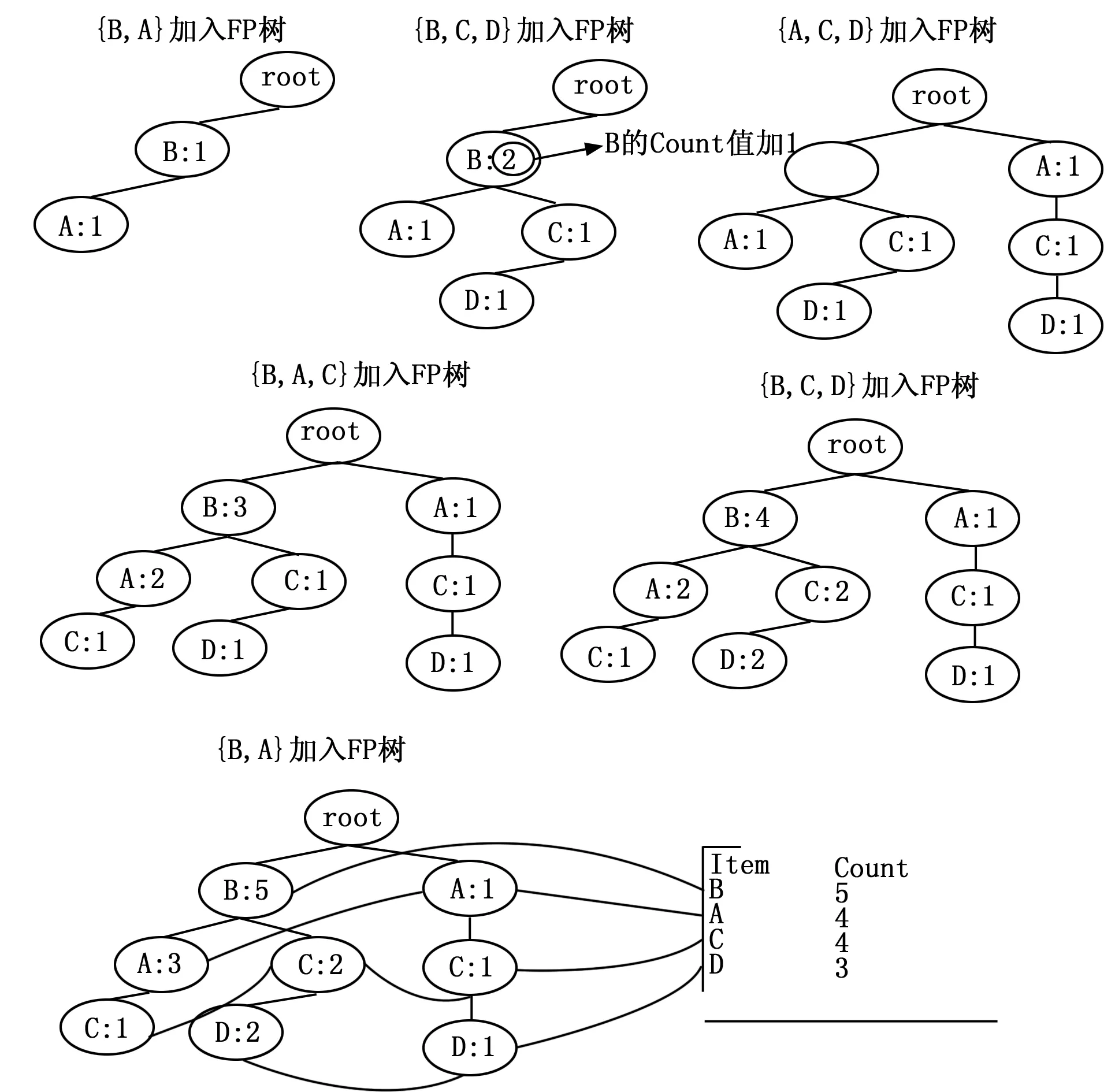
圖1 FP樹構建步驟

2)利用FP樹挖掘頻繁項集:

在得到FP樹之后，可以進行頻繁項集的挖掘。以圖1中構建完成的FP樹為例，首先選擇一分支末端節點“D”，由“D”向根節點倒推，找出所有包含節點“D”的路徑，并找出每個包含“D”的分支:{B,C,D: 2}，{A,C,D: 1}，其中“2”和“1”分別表示分支{B,C,D}和{A,C,D}分別出現2次和1次。分支的“Count”值，由分支后綴節點“D”出現的次數決定。

除去節點“D”，我們得到前綴路徑{B,C: 2},{A,C: 1}，根據前綴路徑，創建一棵條件FP樹。然后獲取前綴路徑的每個節點的前綴路徑，并建立條件FP樹，直到條件FP樹中只包含一個元素時返回(如圖2所示)。最后，得到節點“D”的頻繁項集為{{D},{C,D}}。

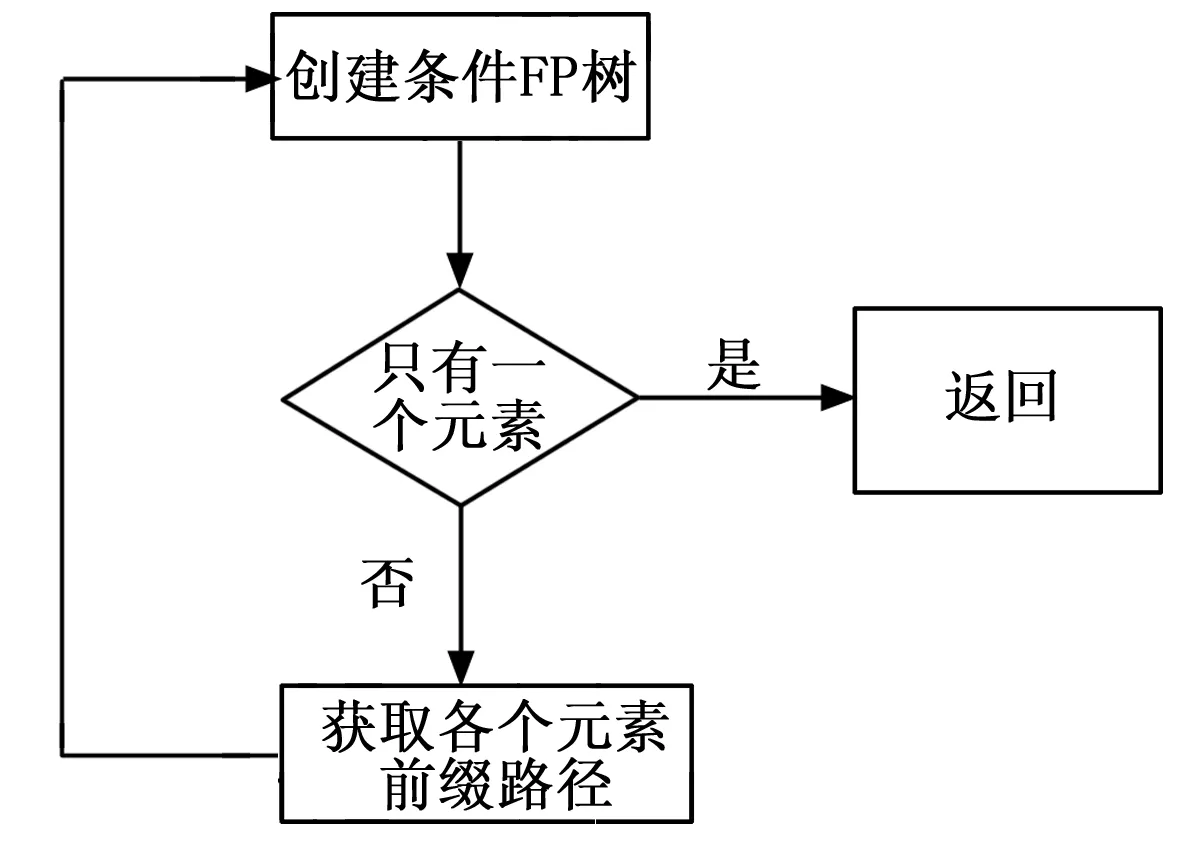
圖2 頻繁項集挖掘流程

3)關聯規則挖掘:

通過FP-Growth算法得到數據的頻繁項集后，針對頻繁項集中的各個頻繁項構建可能的關聯規則。例如，對“D”的頻繁項集中的頻繁項{C,D}而言，可能的關聯規則為{C}->{D}，{D}->{C}。

在得到這些可能的關聯規則后，按如下公式計算置信度:

置信度(A->B)=(同時包含A和B的頻繁項數量)/(包含A的頻繁項數量)，

在示例中:

置信度({C}->{D})=(包含{C,D}的數量:3)/(包含{C}的數量:4)=0.75，

置信度({D}->{C})=(包含{C,D}的數量:3)/(包含{D}的數量:3)=1。

在計算得到所有關聯規則的置信度后，保留大于置信度最小閾值的關聯規則，就可以得到各頻繁項之間的關聯規則。在例子中，由于{D}->{C}的置信度為1，可以知道指令D發出一定會引起電壓C的變化，而{C}->{D}的置信度為0.75，可以得出電壓C的變化有75%的可能是由指令D引起的。

2.2 基于狀態轉換提取的關聯規則算法

對于連續的參數和離散的指令之間的關聯規則挖掘，連續參數的狀態轉換與指令觸發時段之間的聯系對關聯規則的挖掘有至關重要的影響?；跔顟B轉換提取的關聯規則算法，則以此為基礎，在連續參數的曲線中，提取參數狀態轉換位置，再與指令觸發的影響時域進行比對，從而得出參數與指令間關聯規則的一種算法。

基于狀態轉換提取的的關聯規則算法分為數據預處理，提取數據跳變位置，構建狀態矩陣和關聯性分析4個步驟。

1)數據預處理：

對于試驗數據，首先采取預處理措施，除去數據中的非數值和異常跳變數據，以避免異常數據對算法分析的影響。

(1)非數值處理，即將數據中的非數值(NaN)替換成該幀后一幀或前一幀的數據值。

(2)異常跳變數據處理，是在非數值處理后，針對數據中的異常數據進行的異常過濾處理。首先，計算數據標準差，并以±1.5倍標準差為預估異常范圍去篩選異常數據，并得到異常數據集S1。然后，計算數據的二階差分，并以二階差分最大幅度的1/3和10倍標準差作為標準，對異常數據集S1進行二次篩選。最后，對異常數據集S1中的每一條數據進行逐一確認，如果數據前后兩幀數據均為疑似跳變點，且該數據跳變幅度在前后數據幀跳變幅度的2倍以上，則該數據點可以確認為異常數據，并將該數據替換成后一幀或前一幀的數據值。

2)提取狀態轉換位置：

在數據預處理后，取一次差分前段少量數據，濾除大于6倍標準差的數值后，再取其標準差的n倍作為最小閾值標準，大于最小閾值的位置，很有可能是狀態跳轉位置。假設疑似狀態跳轉位置前后的均值和標準差分別是μ1，μ2，σ1，σ2，若其滿足下式則當前位置為狀態轉換位置，并將這個狀態轉換位置加入到狀態轉換位置集S2中。

|μ1-μ2|>n*σ1or|μ1-μ2|>n*σ2

其中：n是置信度水平(默認為3),得到的狀態轉換位置如圖3所示，虛線框內即為數據狀態轉換位置。

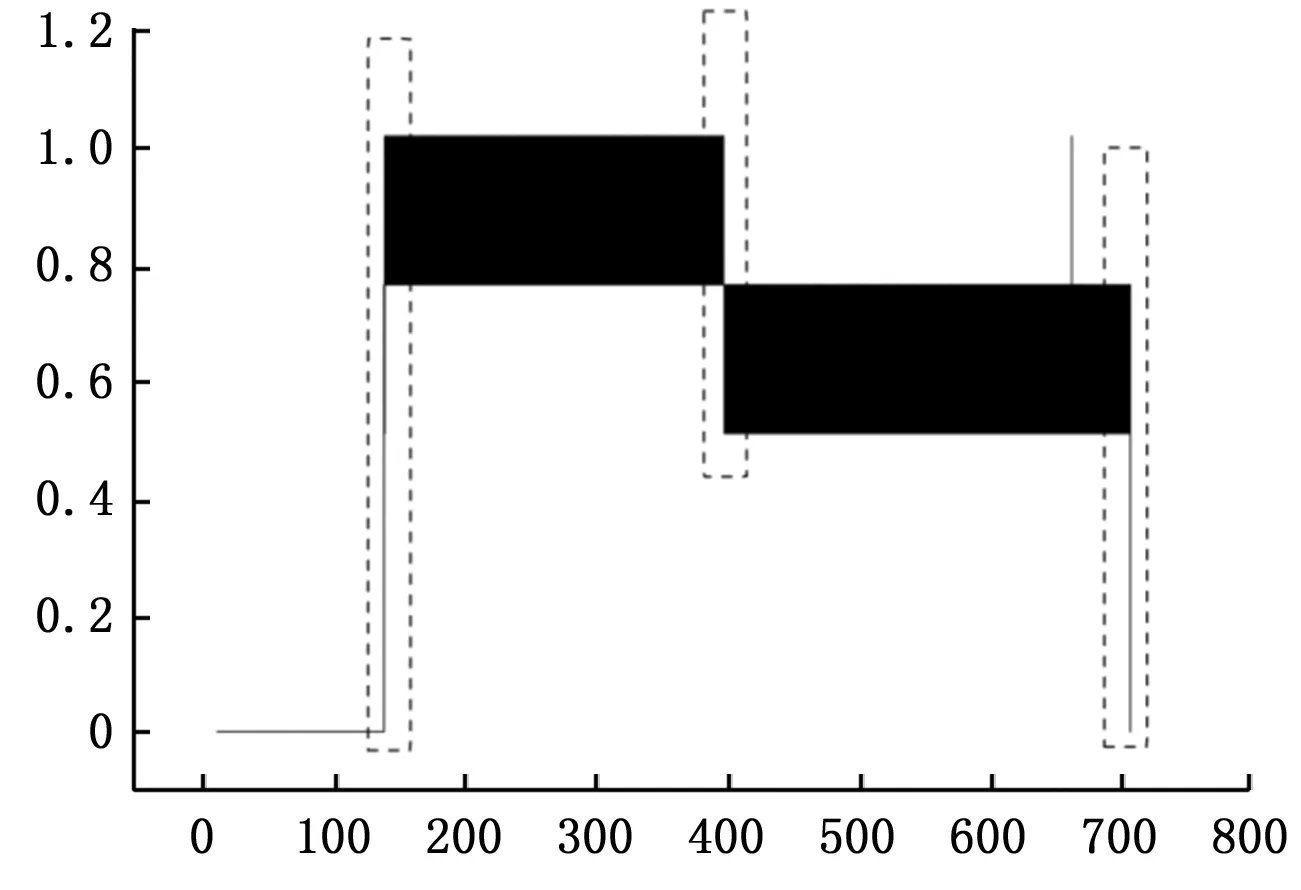
圖3 狀態轉換位置示意圖

3)構建狀態轉換矩陣：

在得到狀態轉換位置集S2后，對于參數的每一幀數據，按時序分別用0和1標注該數據是否發生狀態轉換，即將集合S2中的每一個狀態轉換位置的數據標記為1?；诳紤]參數在指令發出后變化的延遲性，將狀態轉換位置前后m幀的數據范圍作為狀態轉換影響域(轉換影響域的范圍會影響參數關聯性的計算，m值太小可能會導致關鍵關聯丟失，m值太大則會造成過多冗余，這里m值默認為3)，同時狀態標記為1，其他數據標記為0。這樣可以得到如圖4所示的參數狀態轉換矩陣A。

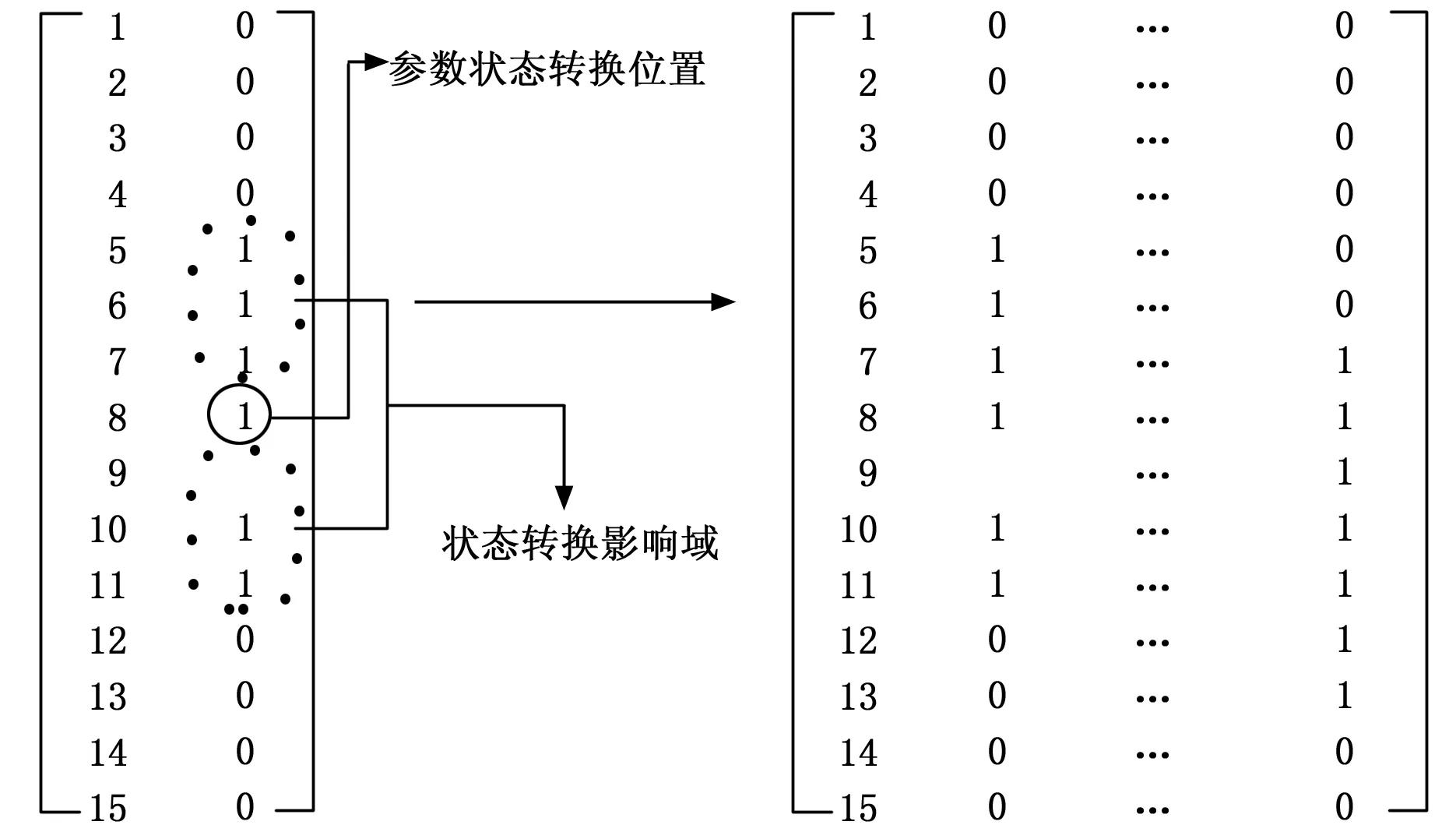
圖4 參數狀態轉換矩陣

4)關聯性計算:

在得到參數狀態轉換矩陣A之后，按照提取矩陣A中的各列數據組成n個一維數組，如圖5所示，并將各個數組分別相乘，得到的值便是兩個參數間的關聯度Cij，其中i,j分別代表兩個不同的參數，即C12表示參數1和參數2之間的關聯度大小。然后，由計算得到的關聯度集合{C}組成參數間的關聯度表，圖5中三角區域為集合{C}的值，其他部分由0填充。

在關聯度表的基礎上，設置最小關聯度MA(minimum association),篩選關聯度表中關聯度大于MA(默認為2)的值，這些值所在的行列表示的參數，可以視為關聯參數對，每一個關聯參數對即為兩條參數相關聯的關聯規則。如圖5中參數1與參數n可以組成關聯參數對，則得到一條參數1與參數n相關聯的關聯規則。

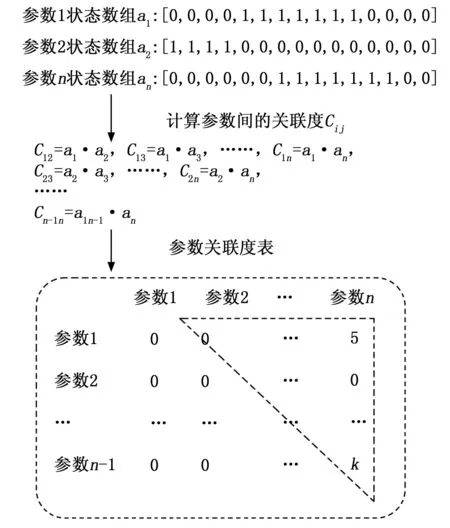
圖5 參數關聯度計算

3 試驗結果與分析

為分析FP-Growth算法和基于狀態轉換提取的關聯規則挖掘算法在遙測參數間關聯規則挖掘的表現和可行性，基于Windows7操作系統，Python3.8和Tensorflow1.15.0等搭建運行環境，運用對比法設計試驗[8]，通過對比兩種算法的準確率和冗余率，給出一個更佳的關聯規則挖掘方法。

3.1 試驗步驟

本次試驗以某次飛行器地面試驗的供電系統遙測數據中的一段為試驗數據，利用系統發出的指令與某電路電流和電壓等三十余萬條數據按時序構成試驗數據集。其中系統指令為離散型數據，電流、電壓等參數隨時間呈連續變化。試驗中驗證數據為人工梳理出的參數與系統指令之間已知的關聯表，如表4所示。

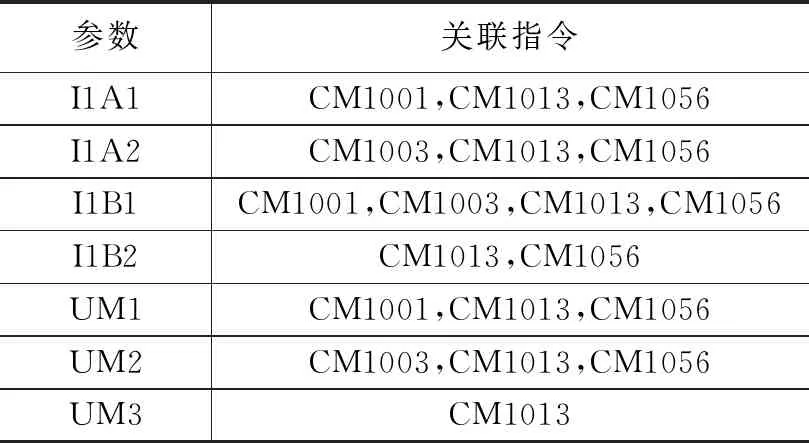
表4 支路電流I、電壓與U指令關聯表(部分)

試驗數據通過分別執行FP-Growth算法和基于狀態轉換提取的關聯規則挖掘算法，對連續變化的參數與離散的系統指令之間的關聯規則進行挖掘，得到參數與指令之間的關聯規則表。再將試驗結果與驗證數據進行對比，計算出挖掘結果的準確率和冗余率。

3.2 試驗結果分析

試驗通過對15個不同參數與5個指令之間已知的31條關聯規則進行挖掘，FP-Growth算法和基于狀態轉換提取的關聯規則挖掘算法分別挖掘到55條和37條規則，兩算法的準確率和冗余率，如表5所示。

根據試驗結果可見，基于狀態轉換提取的關聯規則挖掘結果明顯好于FP-Growth算法。產生這種結果的主要原因一方面與飛行器供電系統遙測數據的實際特征有關，在無指令觸發情況下，參數值變化較小，幾乎無波動。如圖6中參數隨時間變化結果，在指令觸發(圖中虛線處)前后，參數值幾乎無變化，曲線近似為直線。而指令的觸發只是改變參數的穩定域，所以參數呈“斷崖”式變化。

表5 挖掘結果準確率、冗余率

圖6 參數值跳變前后對比圖

另一方面，某些指令觸發次數少，也是導致FP-Growth算法結果準確率低的又一原因，如開機指令(CM1017)和斷電指令(CM1056)，這兩個指令在整個試驗中只能觸發一次，雖然在FP-Growth算法中也設定了指令的作用域，但是這樣的觸發頻率依然很可能被篩選出去，所以無法被挖掘出來。

而基于狀態轉換提取的關聯規則挖掘，則可以很好地利用數據的特點，準確地找到數據跳變的位置即狀態發生轉換的時刻，再去將這些時刻進行關聯計算，從而得出更好的關聯結果。如圖7所示，對于同一參數UM7的挖掘，FP-Growth算法的挖掘結果為CM1001和CM1013兩條指令。而基于狀態轉換提取的關聯規則挖掘算法在CM1001和CM1013基礎上，準確地挖掘出開機指令和斷電指令(即圖中CM1017和CM1056兩條指令)共四條指令。

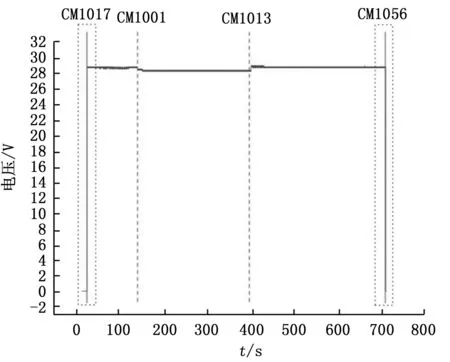
圖7 參數UM7隨時間變化與指令觸發時刻示意圖

在冗余方面，由于基于狀態轉換提取的關聯規則挖掘算法在算法設計初期考慮到狀態轉換存在延遲性，所以可以更好地處理數據發生狀態轉換后到狀態轉換完成之間數據過渡的不穩定期。而FP-Growth算法則是基于頻繁模式，只要數據出現次數高于最小閾值，便可以認為是有效頻繁項，所以無法很好地處理過渡期的非穩定數據。如圖8所示，在挖掘參數UM1與指令之間的關聯時，基于狀態轉換提取的關聯規則算法(圖a)很好地挖掘出3條正確關聯的指令。而FP-Growth算法(圖b)的挖掘結果比正確結果多了兩條，主要因為FP-Growth算法將參數值0也作為一種頻繁項進入算法計算，得到了第一條關聯規則(圖b中CM1017)，還有在第一次指令發出后，參數UM1發生一次跳變(即圖b中CM1001)后有一段時間的過渡期，過渡期的存在導致了FP-Growth算法的第二條冗余關聯(即圖b中CM1003)。

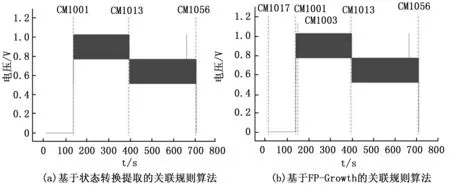
圖8 冗余對比

4 結束語

本文對飛行器遙測數據的關聯規則挖掘算法進行研究，通過試驗對比FP-Growth算法和基于狀態轉換提取的關聯規則挖掘算法在某次試驗數據中的關聯規則挖掘的表現可以看出，基于狀態轉換提取的關聯規則挖掘在數據狀態變化的挖掘和在離散數據量很少時的關聯規則挖掘表現更好于FP-Growth算法。這些研究結論可以為未來飛行器遙測數據間的關聯規則挖掘以及基于關聯規則的飛行器數據異常檢測等方面提供參考。