風電機組健康狀態預測中異常數據在線清洗

馬 然 栗文義 齊詠生

風電機組健康狀態預測中異常數據在線清洗

馬 然1,2栗文義1,2齊詠生2

（1. 內蒙古工業大學能源與動力工程學院 呼和浩特 010050 2. 內蒙古工業大學電力學院 呼和浩特 010080）

風電機組數據采集與監視控制系統（SCADA）運行數據中含有大量異常數據，對風電機組健康狀態預測影響嚴重，為此針對實測風速-功率、轉速-功率數據，提出一種異常數據在線清洗方法。由于機組性能退化過程中數據特征趨于復雜，基于經驗Copula-互信息（ECMI）選擇關鍵特征參量作為數據清洗對象，并基于Copula建立置信等效功率區間描述其非線性與不確定性。針對置信邊界外的堆積點和離群點，結合其時序特征與密度分布建立Copula數據清洗模型（Copula-TFDD），依次進行在線清洗。最后，基于實際數據與人工模擬數據分析模型的精度、運算效率以及對機組健康狀態預測的影響表明，Copula-TFDD能準確并實時地識別各類異常數據，有效提升風電機組健康狀態預測的性能。

風電機組健康狀態預測 數據清洗 特征參量 互信息 Copula理論

0 引言

準確可信的數據采集與監視控制系統（Super- visory Control And Data Acquisition, SCADA）運行數據[1]是風電機組發電性能預測、故障預測與健康管理等工作的基礎。然而，由于機組運行環境惡劣，很多現場采集的數據質量較差，特別是因棄風限電、工況波動等原因導致的數據異常問題尤為突出。高比例異常數據對運行數據的真實規律、特征參量的相關性關系等信息的挖掘與應用影響極大，因此風電機組數據清洗工作至關重要。

風電機組數據清洗方法主要從特征空間的距離、概率和密度等角度界定異常值。文獻[2-5]基于四分位法-聚類分析、最優組內方差、變點分組-四分位、Thompson tau-四分位等概率統計方法對風功率數據的空間分布位置分類以識別離群點與堆積點，但基于分類思想的方法對高比例異常數據的辨識效果不佳。文獻[6]利用離群點檢測算法（Density- based Local Outlier Factor, DLOF）和聚類算法（Density-Based Spatial Clustering Applications with Noise, DBSCAN）識別異常點，并指出后者更有利于風電功率預測，但內存占用大、運算效率低，影響了算法的實用性。文獻[7-8]基于Copula建立風功率數據的概率功率曲線模型，利用異常點的時序特征辨識堆積點，識別效果優于傳統的3-sigma概率統計法；但對于海量風功率數據，單一Copula函數對復雜數據集的適應性有限，而混合Copula函數[8]的參數擬合復雜，影響算法在線運行。上述方法均以風功率數據為清洗對象，主要研究機組發電性能預測，而數據清洗方法在機組健康狀態預測中的應用研究目前仍較少。

在風電機組整機性能預測與健康狀態評估的應用中，有關研究[9-12]指出，模型分析法如神經網絡更適合于異常檢測，而高斯混合模型、主成分分析及其改進算法等概率統計方法對機組性能退化的預測適應性更好。然而，概率統計方法對數據質量要求較高，數據清洗的應用方向不同時，清洗對象、需要清洗的異常數據以及清洗方法均會有所差別，因此有必要對風電機組健康狀態預測中的異常數據清洗工作進行針對性研究。首先，選擇運行數據中可反映機組性能退化的關鍵特征參量構成清洗對象，如風速-功率、轉速-功率數據，而軸溫、油溫等參量作為機組健康狀態預測與故障檢測的重要特征依據，剔除其中的異常點反而可能造成故障信息丟失，不能輕易清洗。其次，確定待清洗的異常數據，包括堆積點與離群點。離群點可能反映了工況變化，在基于模型分析法預測發電性能或故障時可以不清洗[7]，但離群點分散性較大，對其進行合理清洗將有利于基于概率統計方法預測機組的健康狀態[10]。此外，不同機組的運行數據存在采樣周期不同、概率分布特征呈差異化等特點，隨著機組性能的逐漸退化，數據分布特征更趨復雜，這些都對數據清洗方法的通用性、精度、運算效率、穩定性以及工程適用性提出了較高要求。因此，有必要針對風電機組健康狀態預測深入研究運行數據關鍵特征參量的選擇，以及堆積點和離群點的在線清洗方法。

目前，可用于解決運行數據特征參量選擇的方法有Relief、互信息、隨機森林與鄰域粗糙集等[13-16]。其中，Relief和互信息基于相關性度量，屬于過濾法，具有快速高效、獨立于預測模型的優點，但Relief為有監督法，而SCADA數據往往沒有分類標簽；隨機森林屬于封裝法，可與鄰域粗糙集應用于負荷預測或故障識別中對特征集的尋優與約簡。因此，基于互信息選擇與機組運行狀態相關性強的關鍵特征參量有利于簡單、快速地確定清洗對象，并利用Copula函數無需假設數據的分布形態即可描述其實際分布規律的特點，解決互信息計算中聯合概率密度函數估計難的問題。為保證數據清洗方法的識別精度與運算效率，聯合考慮關鍵特征參量的概率分布、時序特征與密度分布：利用單一Copula建立風速-功率、轉速-功率等多元特征參量的置信等效功率區間，解決傳統概率統計方法在樣本分布不均、異常值較多時識別精度低的問題，同時避免采用混合Copula，確保算法的運算效率；僅考慮置信邊界外的可疑數據，結合其時序特征和密度分布依次清洗堆積點與離群點，解決DBSCAN算法無法在線清洗[10-11]的問題；進一步基于Copula模擬實際異常數據，解決數據清洗模型定量分析的問題。

基于上述研究背景，本文針對風電機組健康狀態預測中異常數據的在線清洗進行研究。分析風電機組性能退化過程中的數據特征，在此基礎上，提出基于經驗Copula-互信息（Empirical Copula-based Mutual Information, ECMI）法選擇關鍵特征參量，并基于Copula結合異常值的時序特征與密度分布建立數據清洗模型（Copula-based data cleaning model combining Time-series Features and Density Distribution, Copula-TFDD），對堆積點和離群點等典型異常數據進行在線識別。

1 風電機組運行數據特征分析

風電機組的風功率數據呈帶狀分布，非線性和不確定性明顯。關鍵特征參量散點示意圖如圖1所示。依“bin法”[17]確定反映機組發電性能和運行狀態的重要指標——等效風功率曲線，隨著機組性能的退化該曲線逐漸下移，如圖1a所示。引入置信等效功率區間描述風功率數據的非線性與不確定性，以傳統的3-sigma概率統計法為例，比較機組正常運行和性能退化狀態下的3-sigma曲線發現，后者發生了偏移且波動更為劇烈。由此可知，機組性能逐漸退化時有效數據會發生偏移并與異常數據相混雜，分布特征更趨復雜，而清洗異常點時置信邊界波動劇烈必然會增加數據被誤判與漏判的可能。

進一步分析切入、切出風速間的關鍵特征參量，如圖1中點畫線所示，機組正常運行狀態下的置信邊界外有三類異常點，其典型特征表現為：

（1）堆積點（類型Ⅰ、Ⅱ）。底部或中部呈水平堆積型數據，常因棄風限電、通信故障等引起。圖中類型Ⅰ對應于由專家經驗識別的初篩點，其輸出功率很小或在一段時間內持續小于等于0。類型Ⅱ異常點的輸出功率低于正常出力且在連續一段時間內不（或很少）隨風速變化而變化，這類數據無法直接說明機組是否發生異常，卻會影響對健康狀態的預測，建立符合有效數據分布特征的置信邊界決定了對該類堆積點的識別精度。

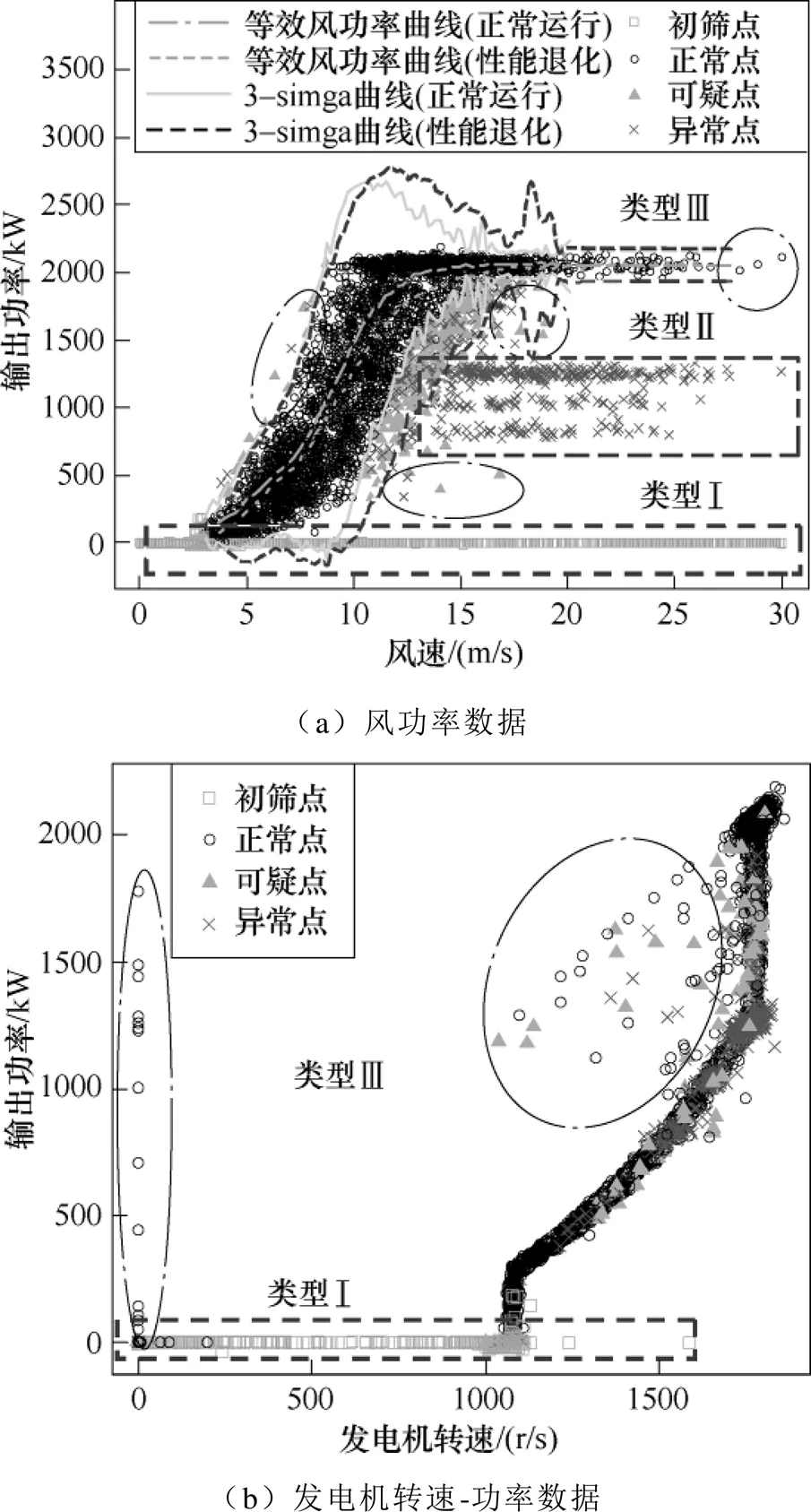
圖1 關鍵特征參量散點示意圖

（2）離群點（類型Ⅲ）。呈分散特征的離群型數據，常因傳感器異常、隨機噪聲、工況波動等引起。離群點的波動具有隨機性，雖然在一定程度上反映了實際工況，但當比例高、分散性大時會影響基于概率統計方法預測機組健康狀態的精度。特別是對于機組因工況波動劇烈而頻繁切換控制所產生的離群點，常表現出時序連續但關鍵參量隨風速的變化不符合物理規律的特點，如圖1b點畫線中的離群點，在圖1a中因落在置信邊界附近而被漏判。因此，數據清洗對象除考慮風功率數據外還應考慮其他關鍵特征參量。

2 基于ECMI的特征參量選擇

2.1 ECMI估計

互信息[18]描述變量間的相關性，計算中利用經驗Copula解決聯合概率密度估計難的問題。

設隨機變量(,)的互信息為(,)，若邊緣概率分布函數F()、F()連續，由Skla定理[19-20]存在唯一Copula函數C,Y(F(), F())擬合聯合累積概率分布函數F,Y(,)。設F()=，F()=，則(,)可由Copula函數的密度函數估計為

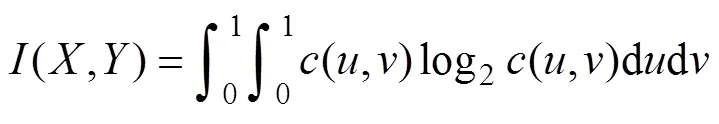
計算(,)的關鍵是準確、快速地估計。采用非參數核密度估計[14, 21]的方法雖然精度高但計算量大、耗時長，因此，本文基于經驗Copula函數的解析法選擇最優Copula函數并估計Copula密度，兼顧計算精度和運算效率。

常用的Copula函數包括橢圓Copula函數族與阿基米德Copula函數族，依據最小距離法計算不同Copula函數與經驗Copula函數的二次方歐式距離，選擇距離最小的Copula函數估計(,)，有

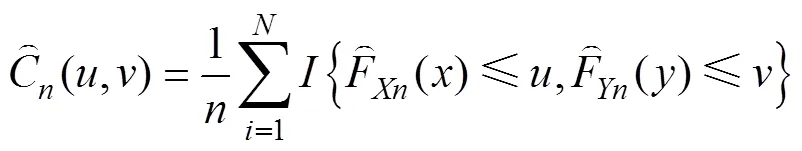
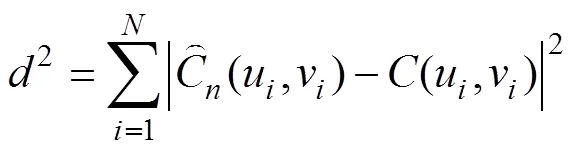
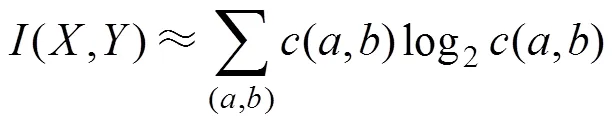
2.2 基于ECMI的特征參量選擇

本文根據SCADA系統標簽選出與機組運行狀態相關的17個變量構成初始特征參量集，共計117 538個時刻點，對應三類特征：條件參量，如風速、機艙溫度等；性能參量，如反映整機狀態的輸出功率、槳距角、轉速等；健康參量，如反映關鍵部件齒輪箱運行狀態的各類軸溫、油溫、振動等。其中，輸出功率作為反映機組整機性能的重要參量，通過選擇與其相關性強即互信息大的關鍵特征參量確定數據清洗對象。

ECMI特征參量選擇策略如圖2所示。①數據預處理：依專家經驗剔除類型Ⅰ異常點，對新數據集按單位區間標準化。②互信息估計：將數據分箱構建經驗Copula；選擇最優Copula函數估計Copula 密度，采用樣本的Kendall秩相關系數代替半參數法擬合參數以提高運算效率；計算各特征參量與輸出功率的互信息并按等級排序，結果見表1。ECMI性能分析如下：

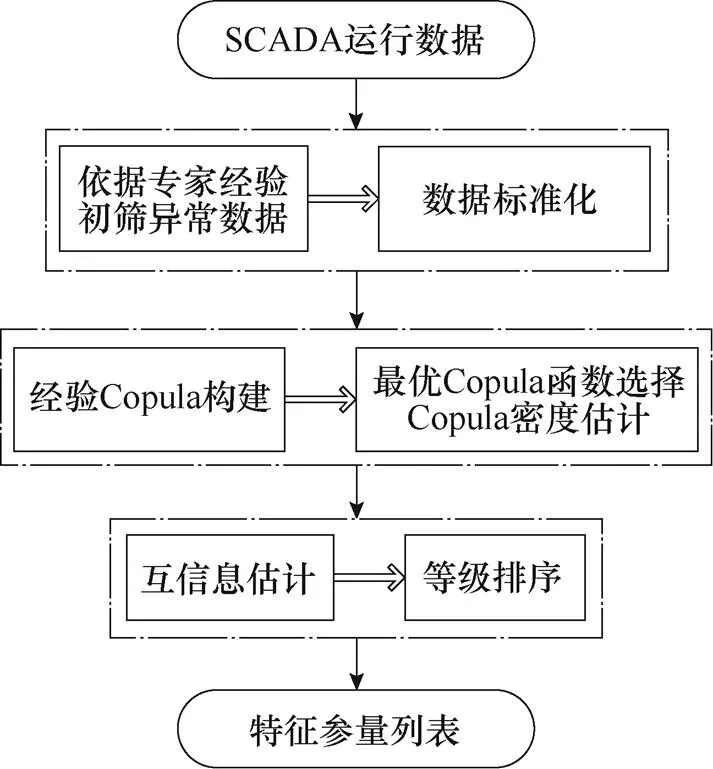
圖2 ECMI特征參量選擇策略

表1 特征參量集等級列表

Tab.1 Rank list of characteristic parameter set

（1）可解釋性。以健康參量為例，各類溫度參量直接反映齒輪箱的健康狀態，一旦高于報警閾值便會導致機組限功率運行或故障停機。從物理角度看，油溫受溫控影響變化平穩，而軸溫波動較明顯，變化趨勢與輸出功率相似，更有利于健康狀態預測，機艙內溫度則反映了工況的變化，也較機艙控制柜溫度更有參考意義。ECMI的等級排序與上述物理知識相一致，故可解釋性良好。

（2）準確性與運算效率。以風速-功率為例，最優Copula類型為Frank，主要描述對稱相關結構，對上下尾部特征均不敏感，而處于中段工況子空間的數據對評估機組健康狀態的貢獻最大[11]，可見由Frank Copula函數描述風功率數據的分布特征有利于保留有效信息。綜合分析等級排序靠前的12個特征參量，其中冗余部分僅保留等級高的參量。ECMI對應的與輸出功率相關性強的參量依次為發電機轉速、風速、齒輪箱輸入軸溫度、齒輪箱側主軸溫度、槳距角2、齒輪箱油溫及機艙內溫度，結果與核密度估計法基本一致，主要差異在于槳距角與軸溫的等級順序，但運算效率遠遠高于后者。

綜上分析，選擇輸出功率、發電機轉速、風輪轉速、風速和槳距角等關鍵特征參量構成數據清洗對象。對于軸溫、油溫等等級較高的健康參量，因其異常值可能反映出工況變化或關鍵部件有異常發生，故不能輕易剔除，但可作為機組健康狀態預測與故障檢測的重要特征依據。

3 基于Copula-TFDD的數據清洗方法

3.1 Copula-TFDD數據清洗模型

由關鍵特征參量確定風速-功率、發電機轉速-功率和風輪轉速-功率為清洗對象后，便能建立數據清洗模型，從而實現堆積點與離群點的有效識別。

1）基于Copula建立置信等效功率區間

Copula函數無需明確數據的分布形態即可準確描述其概率分布特征，因此，基于Copula建立置信等效功率區間來描述清洗對象的非線性與不確定性，認為置信邊界內的數據為符合數據真實分布規律的有效數據，邊界外的數據為可疑數據。

在不同風速或轉速的條件下建立輸出功率的條件概率分布，由其上下分位數對應的概率功率曲線[22]形成置信等效功率區間。基于經驗Copula函數的解析法確定最優Copula函數擬合聯合分布，給定，得條件概率分布函數為

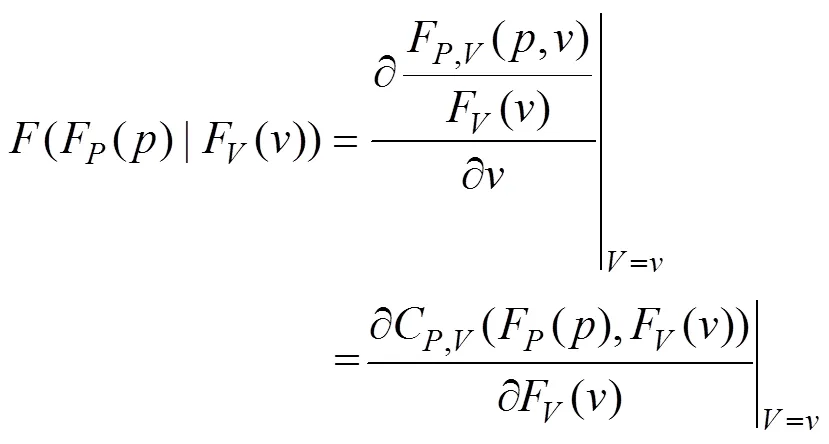
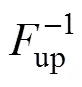
2）基于TFDD清洗異常數據

結合三類典型異常數據的時序特征和密度分布（Time-series Features and Density Distribution, TFDD），分別清洗堆積點與離群點。

堆積點的風速、輸出功率和槳距角等關鍵特征參量具有典型的時序特征，結合工程經驗依次識別類型Ⅰ堆積點和置信邊界外的類型Ⅱ堆積點。類型Ⅲ離群點因其分散性相對于整個數據集不具有典型時序特征，但與有效數據的密度分布不同，因此利用DBSCAN算法[11, 23-24]進行甄別。若直接清洗原始數據集，需要分段處理數據[11]，僅清洗數據量較小的可疑點可以克服算法本身內存占用大、運算速度慢的缺點，保證數據清洗方法的實用性。異常數據判別準則見表2。

表2 異常數據判別準則

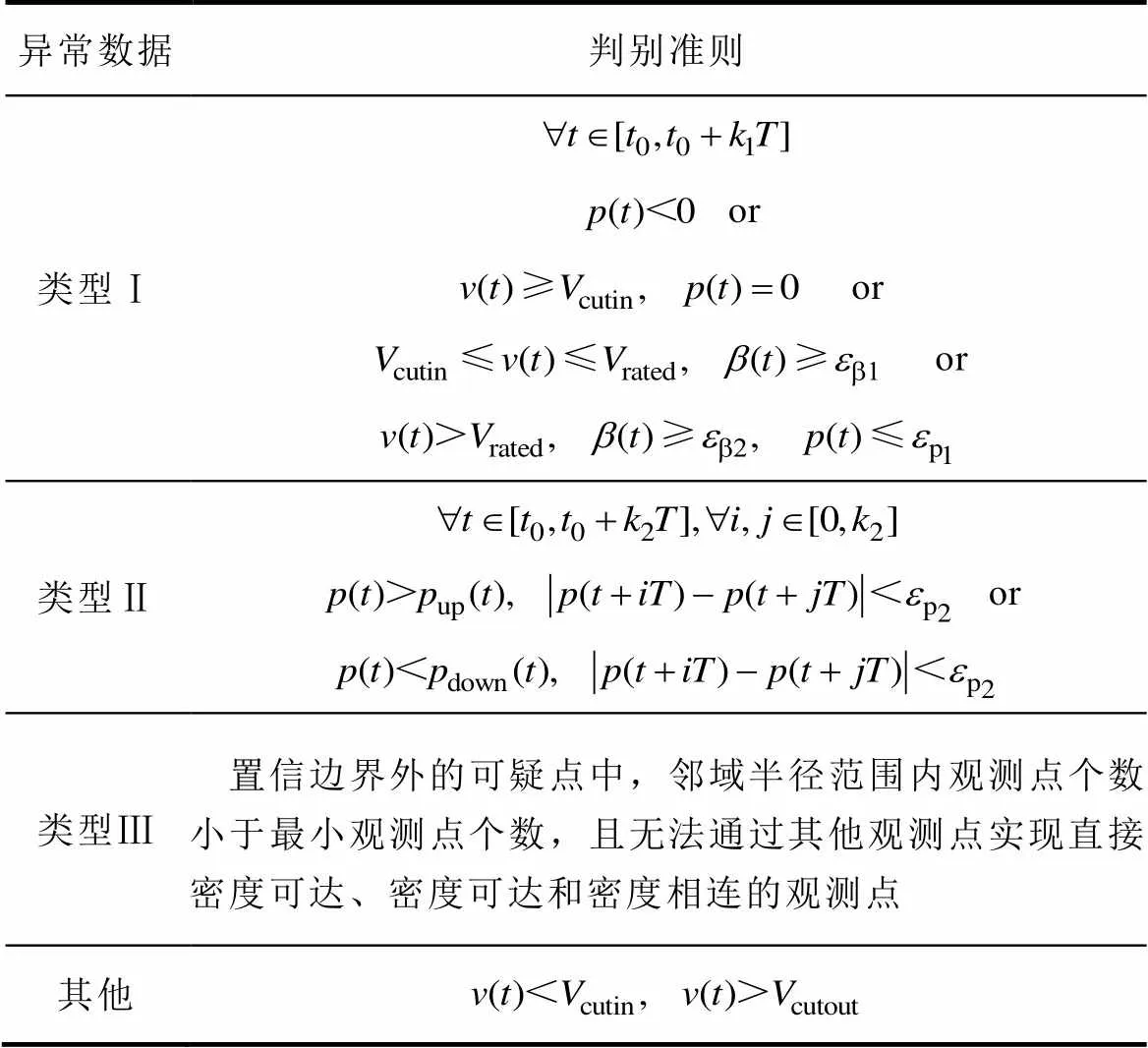
Tab.2 Discriminant criterion of abnormal data

表2中，()、()、()分別為風速、輸出功率和槳距角；up()、down()對應置信邊界；cutin、rated、cutout分別為切入風速、額定風速和切出風速；為單位持續時間；11、2、3取整數；b1、b2、p1、p2為閾值參數，由工程經驗設定。

3.2 Copula-TFDD在線清洗流程

以風速-功率、發電機轉速-功率和風輪轉速-功率為清洗對象，建立Copula-TFDD在線清洗流程，如圖3所示，逐步清洗堆積點和離群點。

（1）模塊1。識別風速-功率數據集中的堆積點。首先，基于專家經驗對原始數據集進行初篩，根據機組正常運行狀態下的數據確定最優Copula函數，適當設置置信概率與不對稱系數，建立初始概率功率曲線；依據判別準則清洗置信邊界外可疑數據中的堆積點，通過重復修正概率功率曲線自適應調整置信邊界，從而提高模型對復雜數據集的適應性；最后，形成新數據集并記錄數據標簽。

（2）模塊2。識別風速-功率數據集中的離群點。針對模塊1的剩余可疑數據，利用DBSCAN算法識別離群點，形成新數據集并記錄數據標簽。

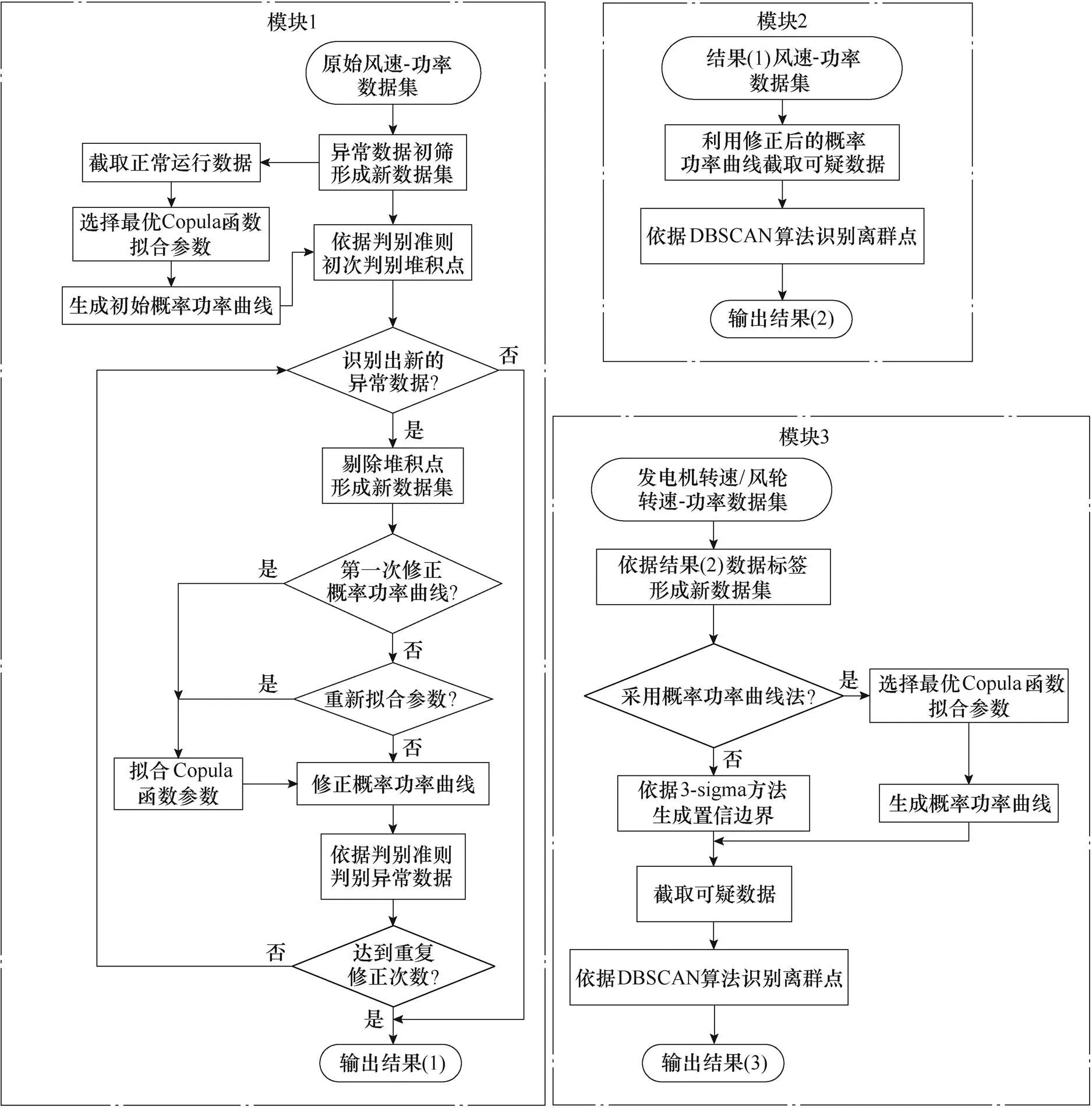
圖3 Copula-TFDD數據清洗模型流程

（3）模塊3。識別發電機轉速/風輪轉速-功率數據集中的離群點。根據模塊2的數據標簽得到新的轉速-功率數據集，因其離群點數量較小，且轉速與功率的相關性較強，故可以利用3-sigma概率統計方法建立置信等效功率區間，以提高運算效率。

3.3 基于Copula人工模擬異常數據

SCADA系統往往沒有數據狀態標簽，為進一步定量分析數據清洗模型的精度與運算效率，相關文獻[7, 22]普遍采用人工模擬異常數據的方法進行驗證，卻并未給出模擬方法。本文利用Copula理論可以模擬多元隨機變量分布特征的特點，人工模擬關鍵特征參量中的異常數據，以定量分析Copula- TFDD的精度與運算效率。

由輸出功率和其他特征參量構成二元隨機變量，要生成服從實際分布F,V(,)的隨機變量(,)，可借助條件分布函數(F()|F())生成一對在(0, 1)區間上服從均勻分布且具有Copula函數C,V(,)的隨機變量(,)，其中= F()，=F()，對和求逆即可得到(,)。

據此，以通信故障、傳感器異常、棄風限電等原因引起的明顯離群點和堆積點為模擬對象，人工構造各類異常數據。首先，基于經驗Copula函數的解析法選擇對應的最優Copula函數模擬各類異常點的分布特征，以輸出功率為條件，隨機生成符合實際分布特征的風速、發電機轉速和風輪轉速等隨機變量；然后，模擬堆積點的時序特征，并以機組典型工作日數據為基礎，建立帶標簽的混合數據集。

4 算例分析

以實際運行數據集和人工模擬混合數據集為研究對象，利用DBSCAN算法、3-sigma-TFDD模型和Copula-TFDD模型進行異常數據清洗仿真，分析模型的精度與運算效率，并將清洗結果應用于風電機組健康狀態預測，驗證本文所提方法的有效性和適用性。

4.1 實際運行數據集異常數據清洗

文中引用的實測數據分別為一臺2MW（機組Ⅰ）和兩臺1.5MW（機組Ⅱ、Ⅲ）風電機組的SCADA運行數據集，3臺機組均因主軸高溫故障停機，故障部件為齒輪箱，基本參數見表3。

表3 風電機組基本參數

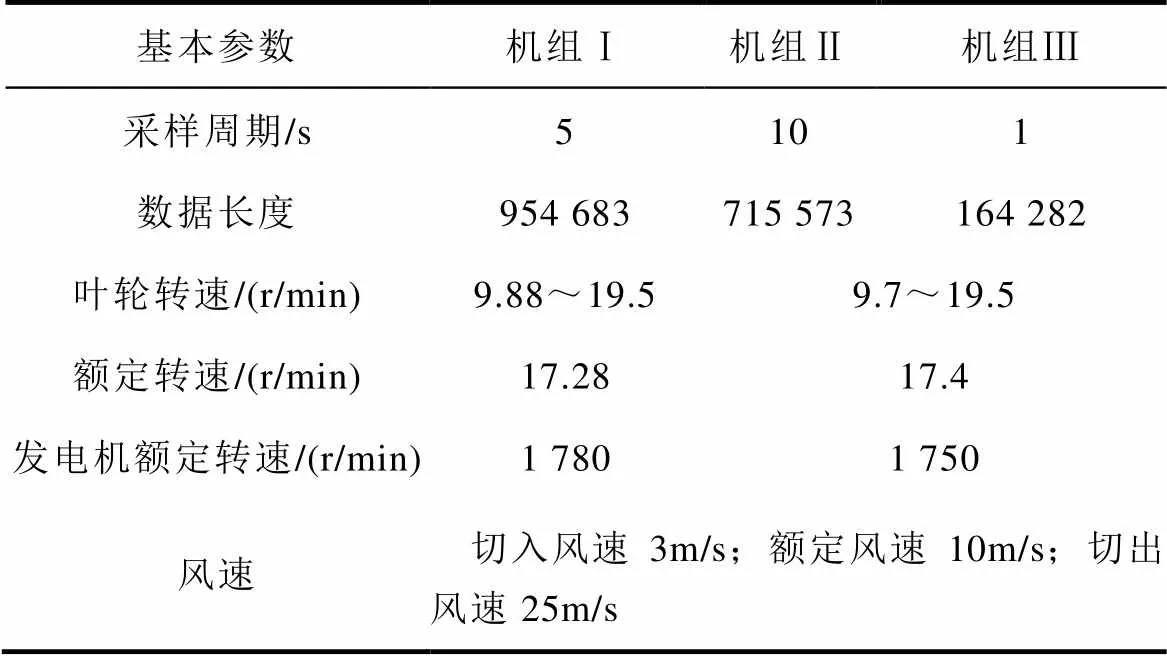
Tab.3 Basic parameters of wind turbine

1）異常數據清洗

Copula-TFDD模型對應風速-功率的清洗結果如圖4所示。以機組Ⅰ為例，對比兩種置信等效功率區間發現，概率功率曲線較3-sigma曲線更接近數據的真實分布且波動較小，可知Copula-TFDD模型較3-sigma-TFDD模型（風速-功率數據的置信邊界采用3-sigma曲線）更有利于減少誤判與漏判。

比較3臺機組的風功率曲線可知，不同機組的數據分布可能不同，機組Ⅰ、Ⅱ對應的Copula函數為反映對稱相關結構的Frank型，其中，機組Ⅰ中三類異常數據均比較典型，機組Ⅱ則主要體現為離群點；機組Ⅲ雖然采樣周期最短，但由于只搜集了故障前3天的數據，并未包含所有工況信息，且異常數據信息較少，對應的Copula函數類型為反映上尾特征的Gumbel型。

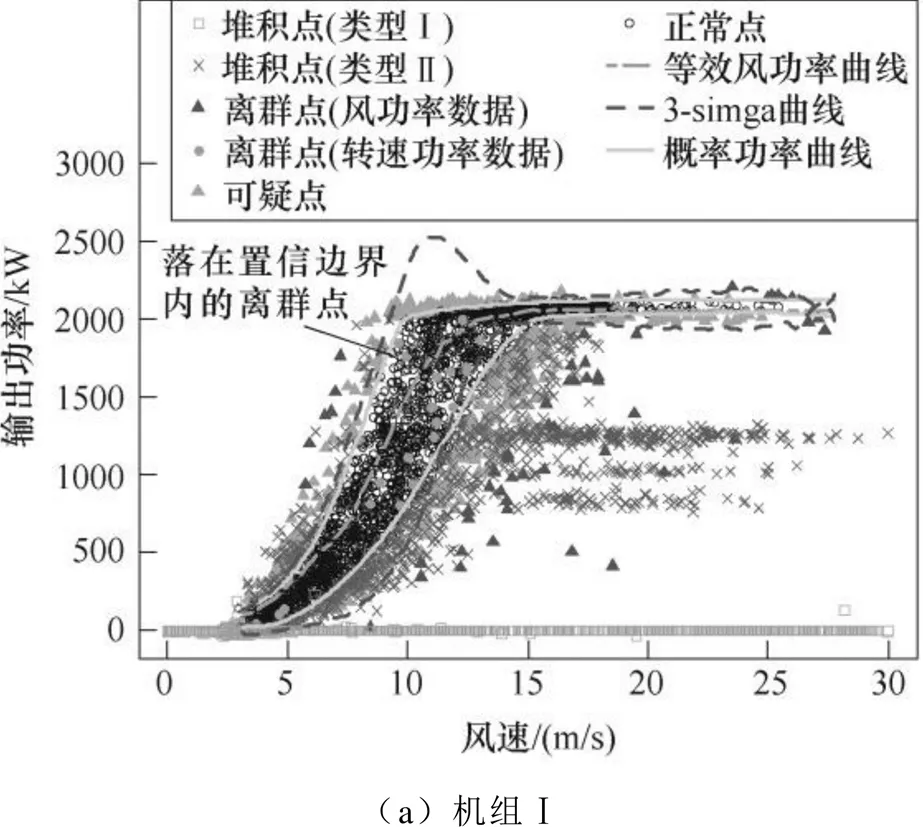
進一步比較Copula-TFDD模型與DBSCAN算法，對應機組Ⅰ的發電機轉速-風速-功率三維清洗結果如圖5所示，圖中點畫線中的因頻繁切換控制產生的離群點在圖4a中落于置信邊界內。可見，Copula-TFDD模型因同時考慮了關鍵特征參量中異常點的時序特征與密度分布，能有效識別落在置信邊界附近的堆積點與邊界內的離群點，而DBSCAN算法只清洗了風功率數據中較明顯的離群點和堆積點，不僅存在漏判，還因分段清洗造成清洗效果不穩定。

分析機組Ⅰ在切入、切出風速間異常數據被剔除前后的剔除率（各風速區間內被剔除的數據占該區間內總數據的比例），DBSCAN算法、3-sigma- TFDD模型和Copula-TFDD模型在四分位間距內的剔除率分別為12.27%～25.01%、12.14%～23.44%和10.73%～22.01%，主要落在20%左右，波動范圍合理。風速范圍兩端的剔除率偏高，存在正常數據被誤判的可能，但這部分數據點較少，且對后續整機性能預測的作用較小，相對于誤判的影響可忽略。

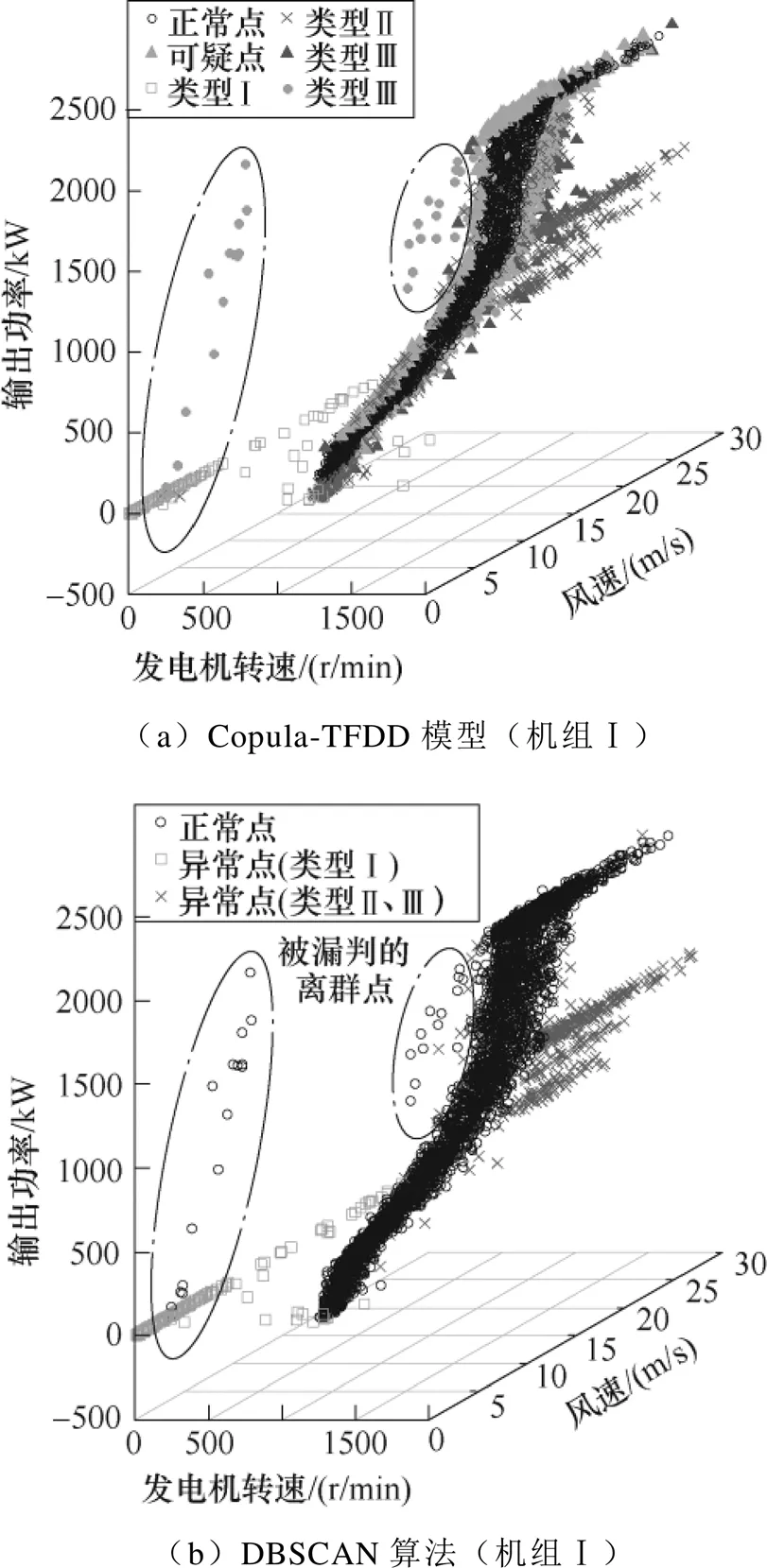
圖5 實際運行數據集清洗結果

分析運算效率。機組Ⅰ對應3-sigma-TFDD模型和Copula-TFDD模型的清洗時間分別為1.7min和9.5min，機組Ⅱ、Ⅲ對應Copula-TFDD模型的清洗時間短于3min，兩種方法均能實現在線清洗，而DBSCAN算法只能離線清洗。

2）異常數據分析

因棄風限電造成的堆積型異常點具有典型的時序特征，可以結合槳距角信息利用判別準則進行清洗，而對于離群點的清洗則需要更為謹慎。

離群點分布分散，主要因隨機誤差、工況波動或限電造成的控制機制頻繁切換等引起，前者屬于偶發，后者通常時序連續但沒有典型的變化規律，因此利用基于密度聚類思想的DBSCAN算法進行清洗。圖4b、圖4c和圖5a中點畫線中的離群點分散性較大，但圖4b、圖4c中虛線中的離群點距離有效數據近，密度較正常運行數據低，若被過度清洗可能會誤刪有效數據。在風機發電性能評估中離群點通常可以不清洗[10]，然而，通過合理設置參數，離群點的清洗有利于基于概率統計方法對整機性能退化過程的預測[10-11]。

3）其他關鍵特征參量分析

以機組Ⅰ的機艙振動與齒輪箱油溫等健康參量為例，分析其他關鍵特征參量的數據清洗工作。機艙振動有效值-風速、齒輪箱油溫-輸出功率的關系分別如圖6和圖7所示，觀察之前的數據清洗結果發現，已清洗的各類異常點特別是離群點均分布在正常范圍，未超報警閾值。

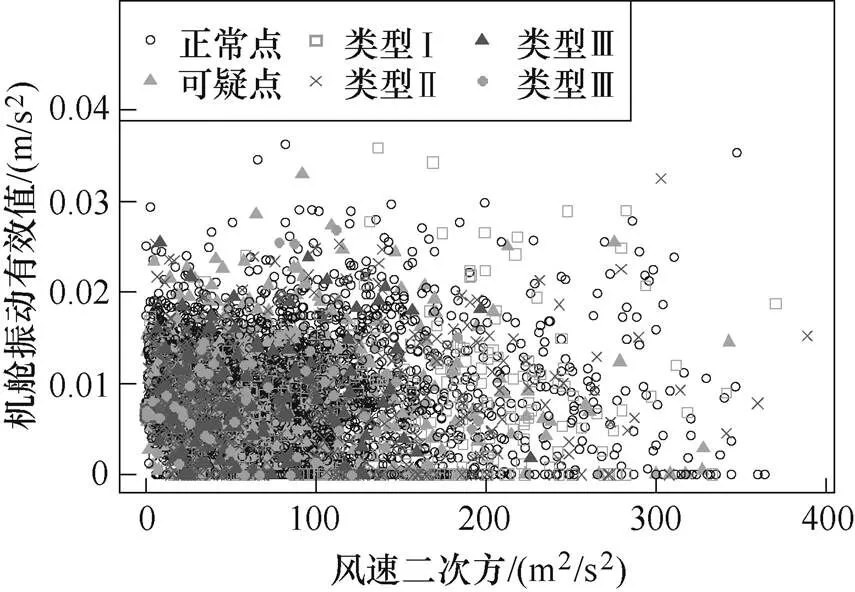
圖6 機艙振動有效值與風速的關系

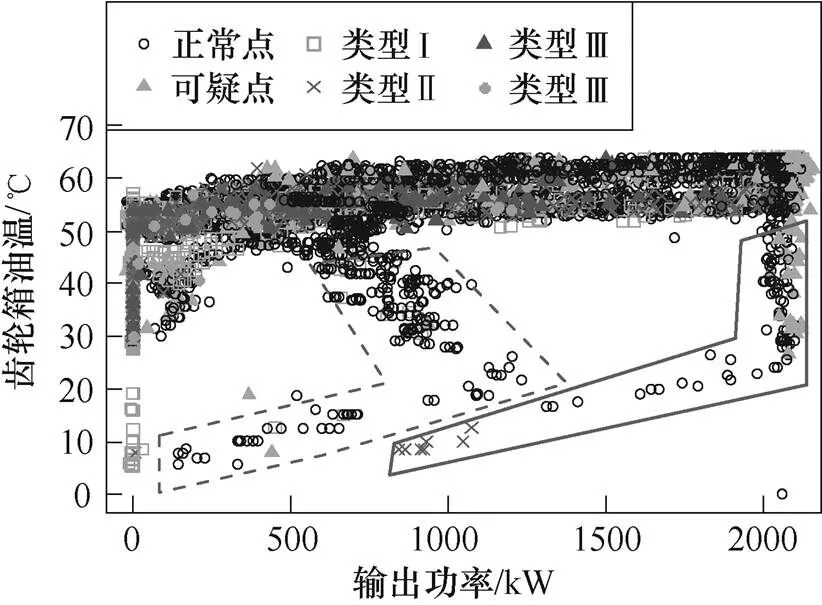
圖7 齒輪箱油溫與輸出功率的關系

圖6中，機艙振動信號變化快速，隨風速增大變化加劇。通常，振動信號對機械故障比較敏感，含有故障信息的振動信號常呈現出分散性較大的離群分布，故對離群點的清洗可能會隱藏故障信息。

圖7中，齒輪箱油溫變化平緩，由于受溫控閥影響，基本不隨功率變化出現明顯波動。對于緩變信號，一般不會出現明顯的離群點。而圖中虛線和實線中的數據則分別為d6和d21兩天的數據，具有典型的時序特征，且呈特殊的密集型分布，這種情況可能是受當日極端氣候影響所致，不排除機組有故障發生，因此不能直接剔除。

健康參量往往反映了機組關鍵部件的健康狀態，因此，本文不對振動與溫度等參量進行清洗。

4.2 人工模擬混合數據集異常數據清洗

為進一步定量分析數據清洗模型的精度與運算效率，以機組Ⅰ在故障前近兩個月（2.21～4.16）的數據為基礎，人工模擬具有代表性的數據集。

首先，建立基礎數據集。表4給出了部分工作日的風速范圍和Copula-TFDD清洗結果。結合日風功率散點圖發現，機組在不同工作日、不同運行工況下數據分布各異且各類異常點占比差異明顯，例如，d1/d38/d45機組運行在切入、切出風速之間，異常點較少，而d4/d20幾乎全部為類型Ⅰ異常點，d52～d56的異常點中類型Ⅱ、Ⅲ占比增大，故障前兩日的風速范圍較大，故障當天機組運行狀態明顯異常。因缺乏氣象數據，同時要確保基礎數據集覆蓋全部工況，并考慮機組性能逐漸退化、氣溫逐漸升高等因素，本文沒有直接對全部數據集抽樣，而是先根據風速條件與數據分布確定各月的典型工作日（占全部數據集70%），再隨機抽樣構成數據集1，其中故障發生當月的數據占比較大。在此基礎上，提取各類異常數據，根據3.3節中人工模擬異常數據的方法分別構造混合數據集2～4，異常數據比例見表5。以數據集2為例，散點示意圖如圖8所示。

表4 典型工作日異常數據比例

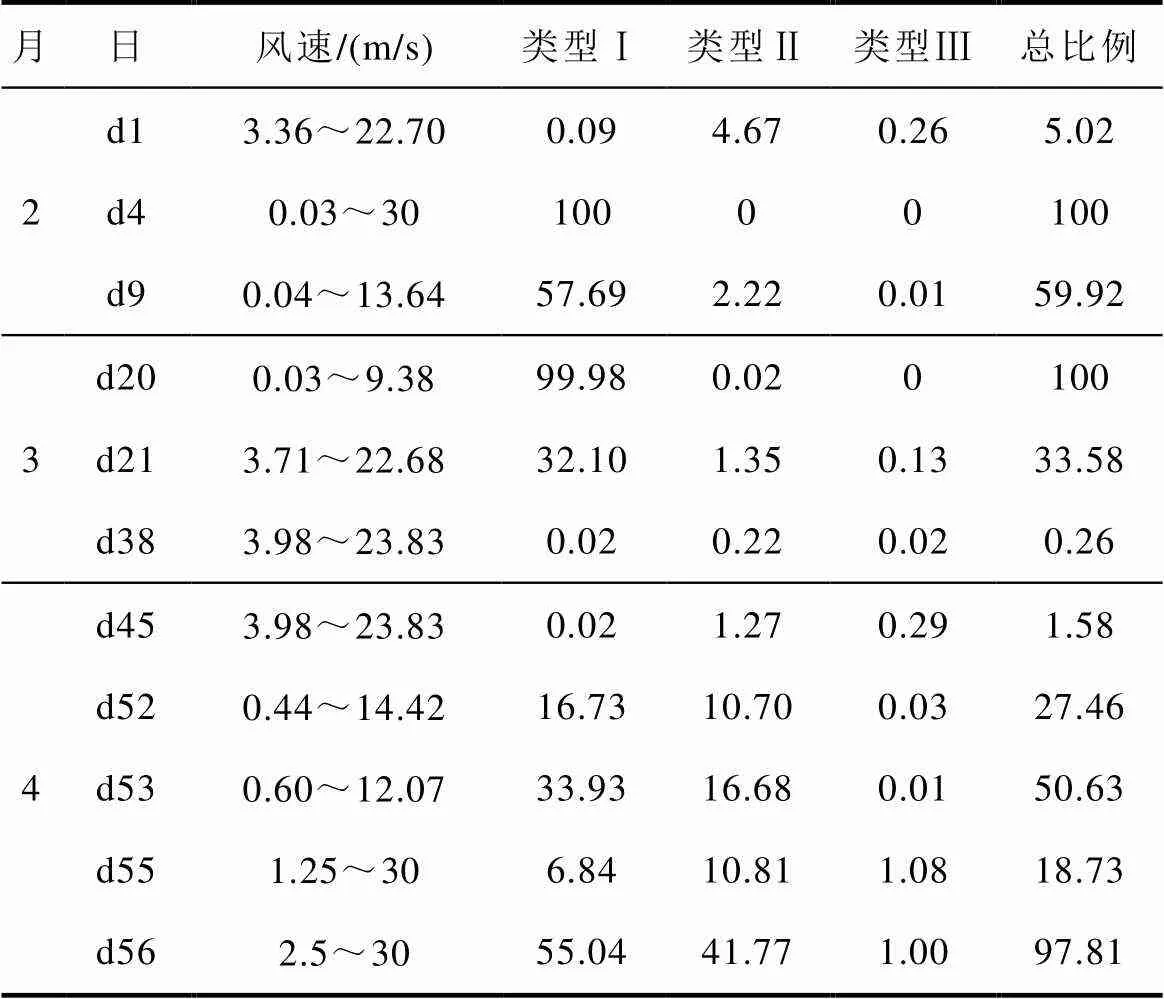
Tab.4 The proportion of abnormal data in typical day（%）

表5 人工模擬異常數據比例

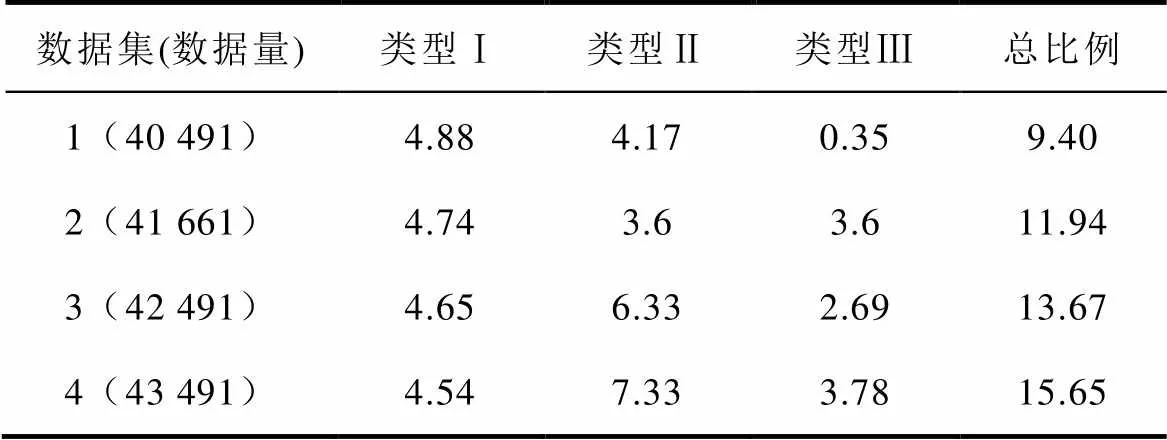
Tab.5 The proportion of artificial abnormal data （%）

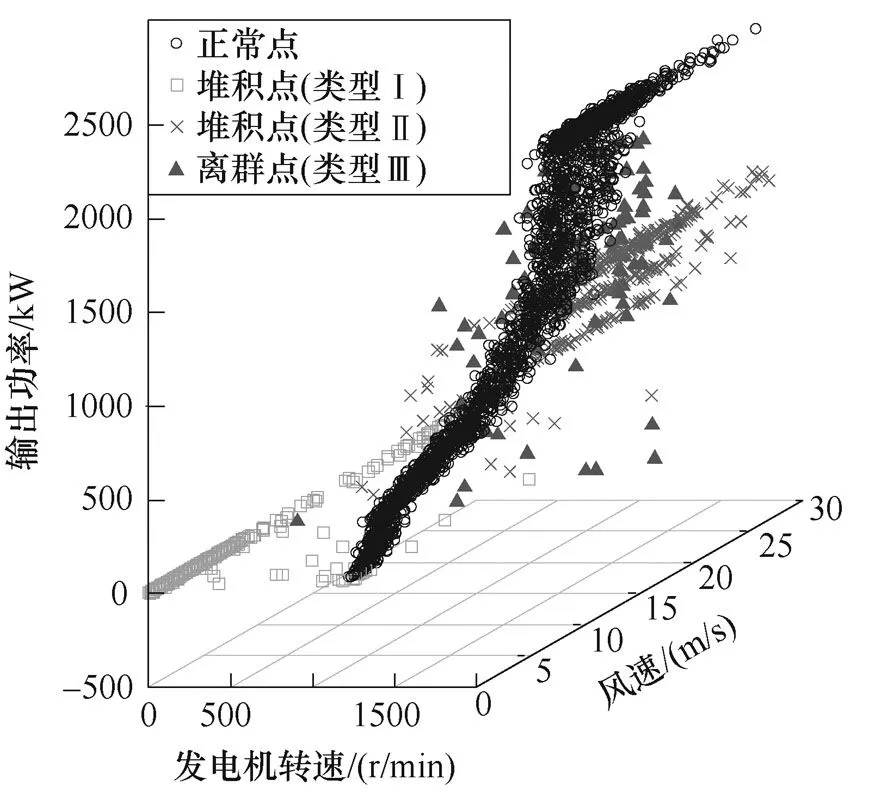
圖8 人工模擬數據集2散點示意圖

采用DBSCAN算法、3-sigma-TFDD模型和Copula-TFDD模型分別清洗數據集1～4，人工模擬混合數據集的統計識別結果見表6。

表6 人工模擬混合數據集的統計識別結果

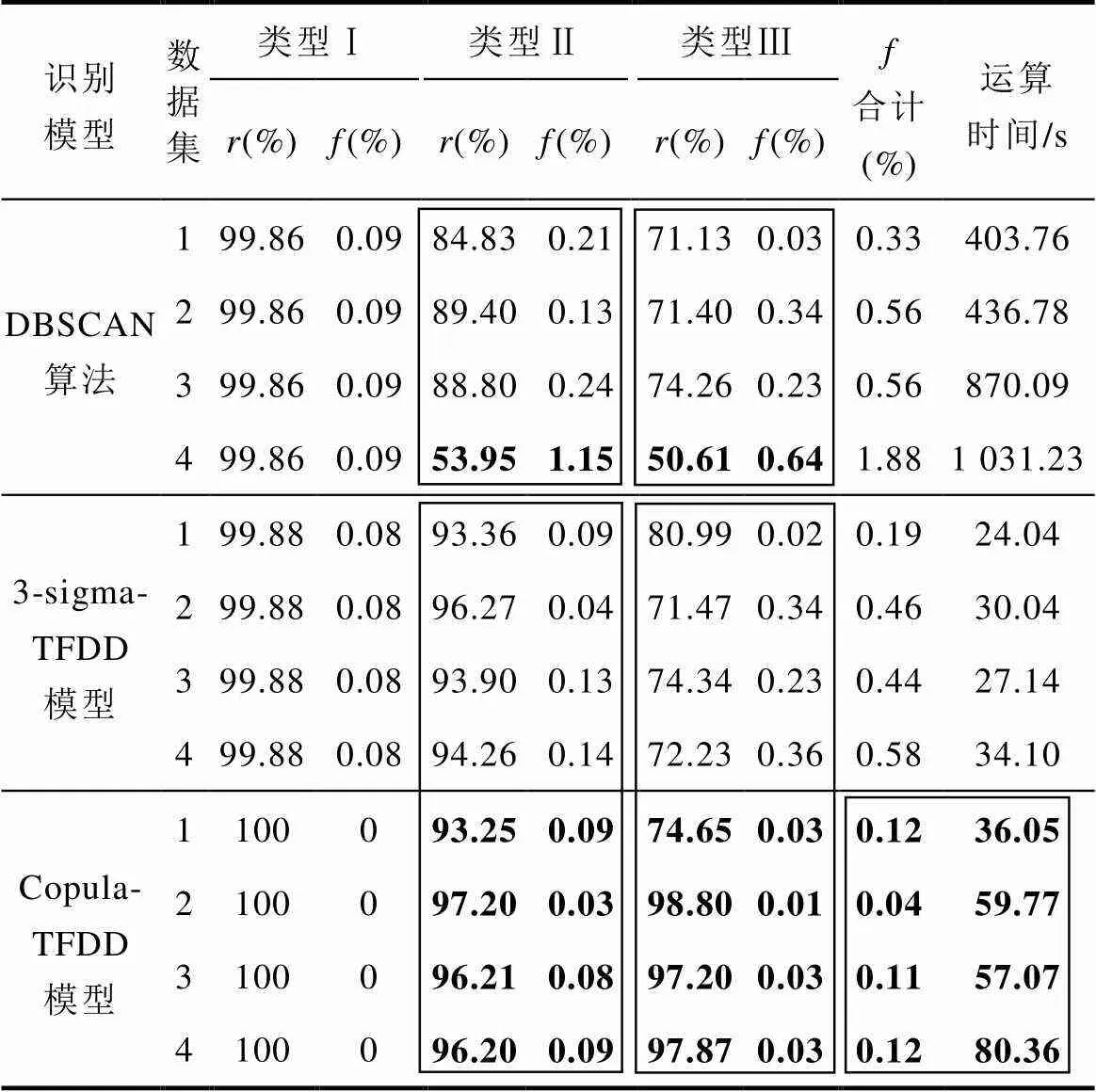
Tab.6 Statistical identification results of artificially generated mixed datasets

較高的識別率說明模型的正確率較高，但有效的清洗模型應同時具有較低的誤識別率[22]。模型精度與運算效率定量分析如下：

（1）堆積點的識別率。三種方法對類型Ⅰ堆積點的識別率均較高；對于類型Ⅱ堆積點，兩種TFDD模型因同時考慮了數據的概率分布、時序特征和密度分布，識別效果均優于DBSCAN算法，當異常點的占比增加時，后者的識別率下降明顯。

（2）離群點的識別率。離群點的數量和分布位置會影響兩種TFDD模型的識別效果。數據集1中離群點雖然只占0.35%，但較多離群點落在了置信邊界內，Copula-TFDD模型的識別率略低于3- sigma-TFDD模型；隨著數據集2～4中離群點的占比增加、概率統計特征波動變大，3-sigma-TFDD模型的識別精度明顯低于Copula-TFDD模型，后者由于更符合數據的實際分布特征，保證較高識別率的同時可保持較小的波動。

（3）誤識別率。三種方法針對不同數據集的誤識別率均較低，因此直接剔除異常點對最終的數據應用影響不大。進一步分析，三種方法的誤識別率依次降低，隨著異常數據的占比增加，各模型的誤識別率均有所升高，但前兩者升高明顯，Copula- TFDD模型的穩定性更好。

（4）運算效率。DBSCAN算法的運算時間最長，而實際運行數據的數據量很大，該方法需要依時間窗分段處理數據集，因此不利于工程應用。兩種TFDD模型的運算速度均較快，雖然3-sigma-TFDD模型的算法簡單、運算效率更高，但Copula-TFDD模型的識別精度更高、更穩定。

綜上分析，兩種TFDD模型都可以有效識別三類典型異常數據，綜合考慮模型的精度、運算效率和穩定性，Copula-TFDD模型在工程應用方面的適應性更強。

4.3 異常數據清洗在機組健康狀態預測中的應用

將機組Ⅰ的清洗結果應用于風電機組健康狀態預測，分析數據清洗方法的適用性。

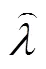
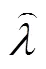
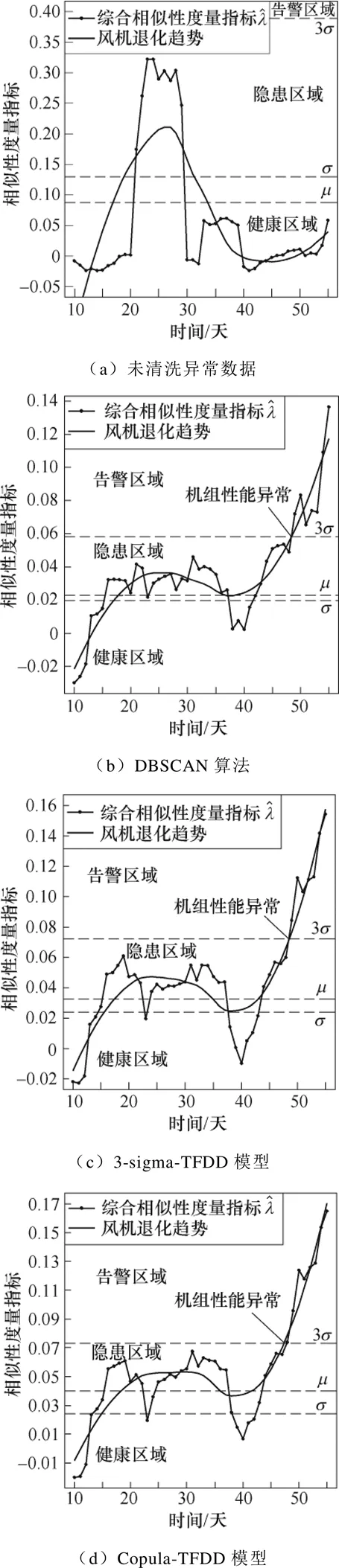
Copula-TFDD模型能在線應用于機組健康狀態預測，雖然較其他數據清洗方法僅能提前一天發現機組性能惡化，但對于風電場提前進行故障診斷、排查維修，避免如齒輪箱損壞等重大故障的發生具有重要意義。

綜上分析，Copula-TFDD模型因綜合考慮了關鍵特征參量的概率分布、時序特征和密度分布，有利于挖掘風速、轉速與輸出功率之間的真實物理規律，適用于風電機組健康狀態預測。

5 結論

針對風電機組健康狀態預測中對異常數據進行在線清洗的實際需求，本文研究得出如下結論：

1）提出基于ECMI的特征參量選擇方法。選擇反映風電機組整機性能的關鍵特征參量構成清洗對象，對實測風速-功率、轉速-功率數據中的堆積點和離群點等典型異常數據進行清洗。

2）基于風電機組實測運行數據的概率分布、時序特征與密度分布提出Copula-TFDD數據清洗模型。該方法可以對具有不同采樣周期和差異化概率分布的運行數據實現在線清洗，且能有效提升機組健康狀態預測的性能。

3）基于Copula給出了人工模擬符合實際異常數據分布特征的數據集的方法。通過對Copula- TFDD的精度、運算效率和穩定性的定量分析，驗證了該數據清洗方法的工程應用性較強。

[1] 陳俊生, 李劍, 陳偉根, 等. 采用滑動窗口及多重加噪比堆棧降噪自編碼的風電機組狀態異常檢測方法[J]. 電工技術學報, 2020, 35(2): 346-358.

Chen Junsheng, Li Jian, Chen Weigen, et al. A method for detecting anomaly conditions of wind turbines using stacked denoising autoencoders with sliding window and multiple noise ratios[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(2): 346-358.

[2] 趙永寧, 葉林, 朱倩雯. 風電場棄風異常數據簇的特征及處理方法[J]. 電力系統自動化, 2014, 38(21): 39-46.

Zhao Yongning, Ye Lin, Zhu Qianwen. Characteristics and processing method of abnormal data clusters caused by wind curtailments in wind farms[J]. Automation of Electric Power Systems, 2014, 38(21): 39-46.

[3] 婁建樓, 胥佳, 陸恒, 等. 基于功率曲線的風電機組數據清洗算法[J]. 電力系統自動化, 2016, 40(10): 116-121.

Lou Jianlou, Xu Jia, Lu Heng, et al. Wind turbine data-cleaning algorithm based on power curve[J]. Automation of Electric Power Systems, 2016, 40(10): 116-121.

[4] 沈小軍, 付雪姣, 周沖成, 等. 風電機組風速-功率異常運行數據特征及清洗方法[J]. 電工技術學報, 2018, 33(14): 3353-3361.

Shen Xiaojun, Fu Xuejiao, Zhou Chongcheng, et al. Characteristics of outliers in wind speed-power operation data of wind turbines and its cleaning method[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3353-3361.

[5] 鄒同華, 高云鵬, 伊慧娟, 等. 基于Thompson tau-四分位和多點插值的風電功率異常數據處理[J]. 電力系統自動化, 2020, 44(15): 156-165.

Zou Tonghua, Gao Yunpeng, Yi Huijuan, et al. Processing of wind power abnormal data based on Thompson tau-quartile and multi-point interpo- lation[J]. Automation of Electric Power Systems, 2020, 44(15): 156-165.

[6] 范曉泉, 杜大軍, 費敏銳. 風電異常測量數據智能識別方法研究[J]. 儀表技術, 2017(1): 10-14.

Fan Xiaoquan, Du Dajun, Fei Minrui. Research on the intelligent identification method for abnormal measurement data of the wind power[J]. Instru- mentation Technology, 2017(1): 10-14.

[7] 楊茂, 翟冠強, 蘇欣. 基于風特征分析的風電機組異常數據識別算法[J]. 中國電機工程學報, 2017, 37(增刊1): 144-151.

Yang Mao, Zhai Guanqiang, Su Xin. An algorithm for abnormal data identification of wind turbine based on wind characteristic analysis[J]. Proceedings of the CSEE, 2017, 37(S1): 144-151.

[8] 胡陽, 喬依林. 基于置信等效邊界模型的風功率數據清洗方法[J]. 電力系統自動化, 2018, 42(15): 18-23, 149.

Hu Yang, Qiao Yilin. Wind power data cleaning method based on confidence equivalent boundary model[J]. Automation of Electric Power Systems, 2018, 42(15): 18-23, 149.

[9] Edzel L, Dustin B, Hossein D A, et al. Wind turbine performance assessment using multi-regime modeling approach[J]. Renewable Energy, 2012, 45: 86-95.

[10] Jia Xiaodong, Jin Chao, Buzza M, et al. Wind turbine performance degradation assessment based on a novel similarity metric for machine performance curves[J]. Renewable Energy, 2016, 99: 1191-1201.

[11] 馬然, 栗文義, 齊詠生. 基于風功率數據的風電機組性能預測與健康狀態評估[J]. 可再生能源, 2019, 37(8): 1252-1259.

Ma Ran, Li Wenyi, Qi Yongsheng. Performance degradation prognostic and health assessment using wind power data for wind turbine generation unit[J]. Renewable Energy Resources, 2019, 37(8): 1252- 1259.

[12] Jia Xiaodong, Jin Chao, Buzza M, et al. A deviation based assessment methodology for multiple machine health patterns classification and fault detection[J]. Mechanical Systems and Signal Processing, 2018, 99: 244-261.

[13] 王正宇, 張揚帆, 段向陽, 等. 基于Relief算法的風電機組故障特征參數提取方法[J]. 華北電力技術, 2017(10): 57-62.

Wang Zhengyu, Zhang Yangfan, Duan Xiangyang, et al. Selection method of fault characteristic parameters for wind turbine based on Relief algorithm[J]. North China Electric Power, 2017(10): 57-62.

[14] Du Mian, Yi Jun, Peyman M, et al. A parameter selection method for wind turbine health management through SCADA data[J]. Energies, 2017, 10(2): 253.

[15] 鄭睿程, 顧潔, 金之儉, 等. 數據驅動與預測誤差驅動融合的短期負荷預測輸入變量選擇方法研究[J]. 中國電機工程學報, 2020, 40(2): 487-500.

Zheng Ruicheng, Gu Jie, Jin Zhijian, et al. Research on short-term load forecasting variable selection based on fusion of data driven method and forecast error driven method[J]. Proceedings of the CSEE, 2020, 40(2): 487-500.

[16] 王爽心, 郭婷婷, 李蒙. 風電機組變工況變槳系統異常狀態在線識別[J]. 中國電機工程學報, 2019, 39(17): 5144-5152, 5295.

Wang Shuangxin, Guo Tingting, Li Meng. On-line abnormal state identification of pitch system based on transitional mode for wind turbine[J]. Proceedings of the CSEE, 2019, 39(17): 5144-5152, 5295.

[17] IEC 61400-12-1: 2017-03(en-fr). In: wind energy generation systems-part 12-1: power performance measurements of electricity producing wind tur- bines[S]. Geneva, Switzerland: International Elec- trotechnical Commission (IEC), 2017.

[18] 石訪, 張林林, 胡熊偉, 等. 基于多屬性決策樹的電網暫態穩定規則提取方法[J]. 電工技術學報, 2019, 34(11): 2364-2374.

Shi Fang, Zhang Linlin, Hu Xiongwei, et al. Power system transient stability rules extraction based on multi-attribute decision tree[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2364-2374.

[19] 李霞. Copula方法及其應用[M]. 北京: 經濟管理出版社, 2014.

[20] 沈小軍, 周沖成, 呂洪. 基于運行數據的風電機組間風速相關性統計分析[J]. 電工技術學報, 2017, 32(16): 265-274.

Shen Xiaojun, Zhou Chongcheng, Lü Hong. Statistical analysis of wind speed correlation between wind turbines based on operational data[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 265- 274.

[21] 徐玉琴, 陳坤, 李俊卿, 等. Copula函數與核估計理論相結合分析風電場出力相關性的一種新方法[J]. 電工技術學報, 2016, 31(13): 92-100.

Xu Yuqin, Chen Kun, Li Junqing, et al. A new method analyzing output correlation of multi-wind farms based on combination of Copula function and kernel estimation theory[J]. Transactions of China Electrotechnical Society, 2016, 31(13): 92-100.

[22] 龔鶯飛, 魯宗相, 喬穎, 等. 基于Copula理論的光伏功率高比例異常數據機器識別算法[J]. 電力系統自動化, 2016, 40(9): 16-22, 55.

Gong Yingfei, Lu Zongxiang, Qiao Ying, et al. Copula theory based machine identification algorithm of high proportion of outliers in photovoltaic power data[J]. Automation of Electric Power Systems, 2016, 40(9): 16-22, 55.

[23] 周賢正, 陳瑋, 郭創新. 考慮供能可靠性與風光不確定性的城市多能源系統規劃[J]. 電工技術學報, 2019, 34(17): 3672-3686.

Zhou Xianzheng, Chen Wei, Guo Chuangxin. An urban multi-energy system planning method incor- porating energy supply reliability and wind- photovoltaic generators uncertainty[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3672-3686.

[24] Ester M, Kriegel H P, Sander J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[J]. Proceedings of the Second International Conference on Knowledge Discovery and Datamining, 1996, 96: 226-231.

Online Cleaning of Abnormal Data for the Prediction of Wind Turbine Health Condition

1,21,22

（1. College of Energy and Power Engineering Inner Mongolia University of Technology Hohhot 010050 China 2. College of Electrical Engineering Inner Mongolia University of Technology Hohhot 010080 China）

Wind turbine (WT) supervisory control and data acquisition (SCADA) data contains a large number of abnormal data, which has a serious impact on the prediction of WT health condition. Therefore, an online cleaning method for abnormal data is proposed according to the measured wind-power and rotate speed-power data. Due to the complexity of data features in the process of WT performance degradation, key characteristic parameters are selected as data cleaning objects based on empirical Copula-based mutual information (ECMI), and the nonlinearity and uncertainty are described by establishing confidence equivalent power interval calculated with Copula. Accordingly, the Copula-based data cleaning model combining the time-series features and density distribution (Copula-TFDD) of abnormal points is established, and online cleaning for the stacking points and outliers outside the confidence boundary is performed in turn. Finally, through the actual data and the simulation data, the accuracy and efficiency of Copula-TFDD are analyzed, and the influence on the prediction of WT health condition is also analyzed. The results show that Copula-TFDD can accurately and real-time identify various abnormal data, effectively improving the prediction performance of WT health condition.

Prediction of wind turbine health condition, data cleaning, characteristic parameters, mutual information, Copula theory

TK83

10.19595/j.cnki.1000-6753.tces.200278

國家自然科學基金項目（61763037）、內蒙古自治區高等學校科學研究項目（NJZY21305）和內蒙古自治區科技計劃項目（2019，2020GG028）資助。

2020-03-18

2020-07-20

馬 然 女，1982年生，講師，博士研究生，研究方向為風電機組故障診斷與健康管理。E-mail: maran007@imut.edu.cn

栗文義 男，1963年生，教授，博士生導師，研究方向為新能源發電技術。E-mail: lwyyyll@vip.sina.com（通信作者）

（編輯 崔文靜）