基于離散余弦變換的積分因子方法求解非線性Allen-Cahn方程

張榮培, 霍俊蓉, 楊程程

(沈陽師范大學 數學與系統科學學院, 沈陽 110034)

0 引 言

為描述晶體中的反相位邊界運動, Allen和Cahn于1979年提出Allen-Cahn方程[1],可以用于描述鐵合金溶液冷卻過程中結晶固體相分離運動。它是一個二階非線性拋物方程,對于不同的物理體系具有不同的自由能形式。Allen-Cahn方程及其各種變形在圖像分析[2]、晶體的生長[3]、平均曲率運動[4]和隨機擾動[5]等實際問題中都發揮著極為重要的作用。由于此類相場模型沒有真解,所以采用有效的數值方法來進行模擬就顯得尤為重要。

近年來,有很多專家和學者對Allen-Cahn 方程的數值逼近方法進行了研究,包括有限元方法[6],有限差分法[7]、譜方法[8-9]、間斷有限元方法[10]和無網格方法[11]等。另外,在處理高維問題時,算子分裂方法[12]也是一種求解復雜問題的有效策略。

本文應用二階中心差分方法離散Allen-Cahn方程,利用Kronecker積寫出二維拉普拉斯算子的微分矩陣,得到一組非線性常微分方程組。接下來發展積分因子方法進行時間離散。在時間離散過程中,應用Kronecker積的性質將微分矩陣進行譜分解,結合快速余弦變換,可以快速地進行時間離散。

1 數值方法

本文考慮以下形式的非線性Allen-Cahn方程的數值解:

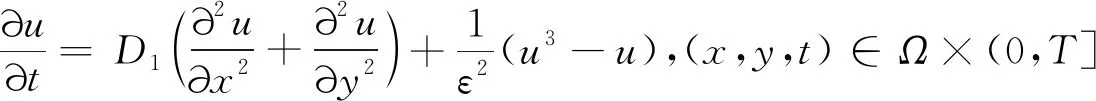
(1)

邊界和初始條件如下:

1.1 空間離散

設u在網格節點(xi,yj)的數值解為ui,j,由齊次Neumann邊界條件,在網格內部點(xi,yj)和邊界處的二階導數差分格式分別為

定義離散解ui,j,1≤i≤Nx,1≤j≤Ny為Nx×Ny階的矩陣U。由差分格(4)式和(5)式,得到該方程在x,y方向的微分矩陣分別為Bx和By,其中矩陣Bx為Nx×Nx階的矩陣,(Bx)i,i=2,i=2,…,Nx-1,(Bx)i,i-1=-1,i=2,…,Nx,(Bx)i,i+1=-1,i=1,…,Nx-1,(Bx)1,1=(Bx)Nx,Nx=1,矩陣Bx中其他位置的元素均為0。同理有By為Ny×Ny階的矩陣。

設Ix,Iy分別為Nx,Ny階單位矩陣,將解矩陣向量化后得

U=vec(U)=(u1,1…uNx,1,u1,2…uNx,2,…,u1,Ny…uNx,Ny)T

(6)

利用(4)式～(5)式以及Kronecker積的定義,可以將(1)式的二階中心差分格式寫成如下形式:

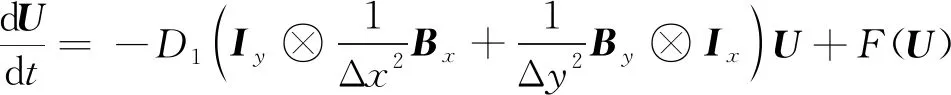
(7)

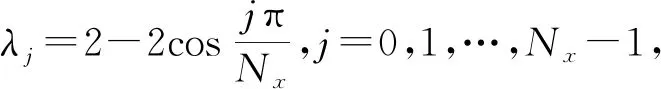
證明 首先考慮另外一個特征值問題:

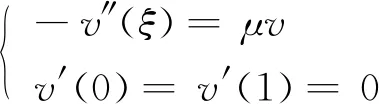
(8)

μ是特征方程的特征值,v為相應的特征函數。將求解區域離散成Nx個網格,

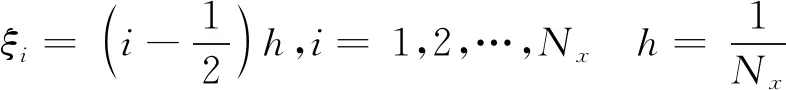
(9)

(8)式的特征方程為

λ2+μ=0

(10)

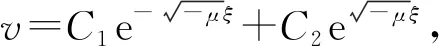
2) 當μ=0時,特征方程通解為v=C1+C2ξ,由條件(8),可得v=C1,求得特征值μ=0。

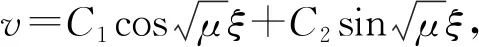
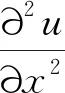
yj=(cosjπξ1,…,cosjπξNx)T,j=0,1,…,Nx-1

(11)

利用三角函數的和差化積公式可以驗證Bxyj=λjyj,j=0,1,…,Nx-1,見附錄。定理1證畢。

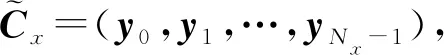
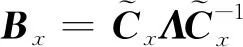
(12)

同理,對By也可得類似的結果。

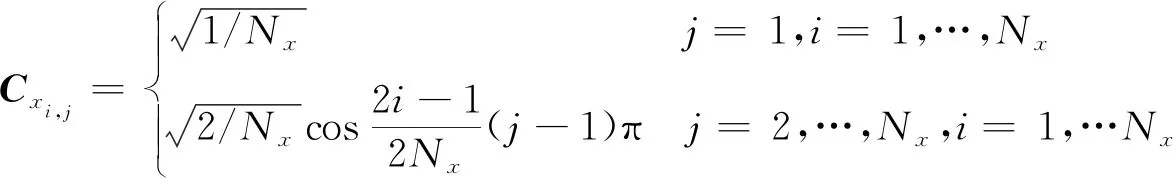
(13)

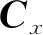
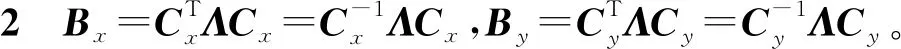
(14)

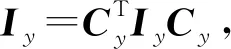
同理有

By?Ix=(Cy?Cx)-1(Λy?Ix)(Cy?Cx)

(16)

結合(15)式和(16)式可以得到

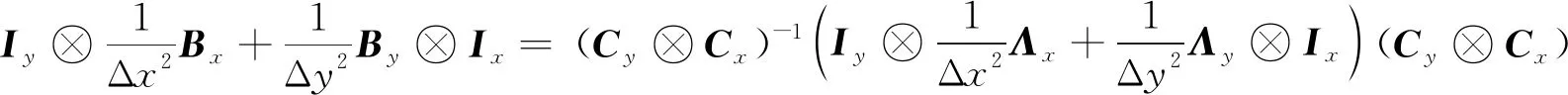
(17)

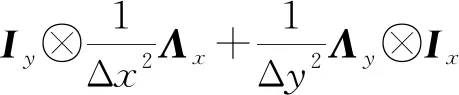
(18)

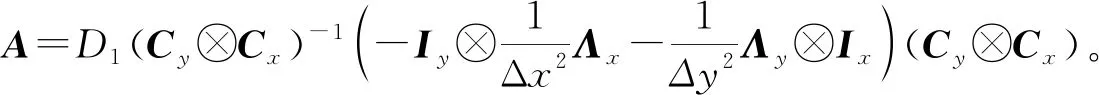
1.2 時間離散

下面應用積分因子法對(18)式進行求解,將(18)式兩端同時左乘e-At,并從tn到tn+1=tn+Δt進行積分得到

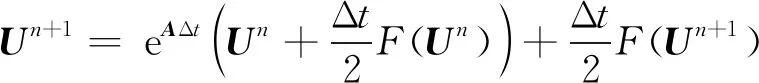
(19)

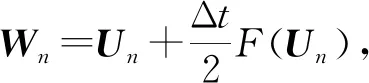
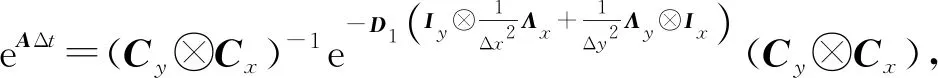
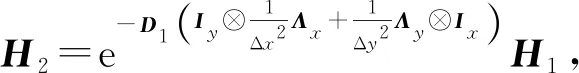
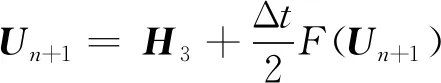
(20)

2 數值實驗

應用本文提出的有限差分法和積分因子法求解下面的數值算例。考慮二維計算區域Ω=[-1,1]2,針對具有齊次Neumann邊界條件的方程(1)進行求解。初值選取形狀像啞鈴的函數,見圖1(a)所示。

選取參數ε=0.05,并在每個空間方向上取512個等分點,時間步長Δt=5×10-5。選取t1=3.53×10-2,t2=7.98×10-2,t3=1.18×10-1這3個時間點,數值結果列在圖1。

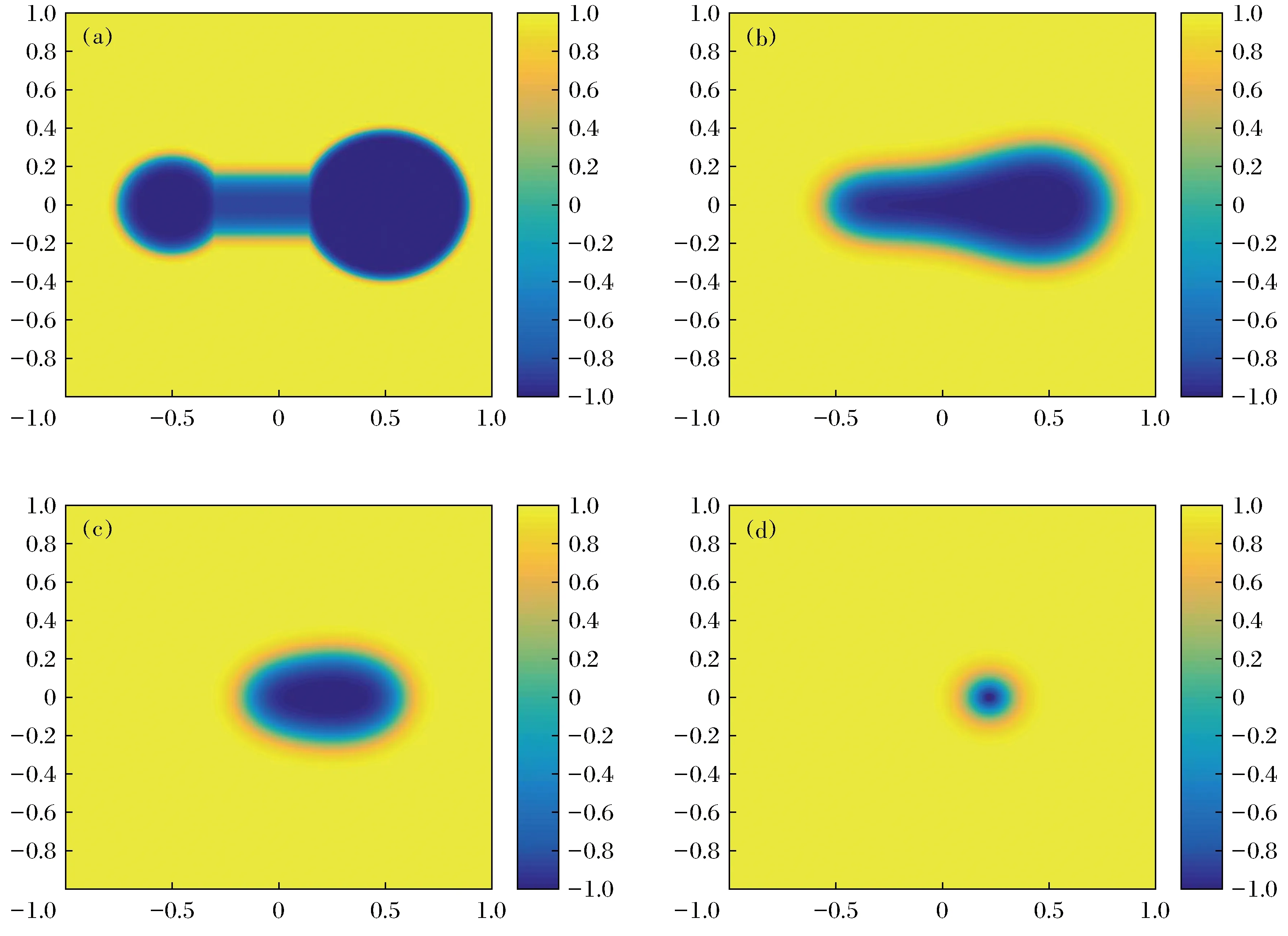
圖1 算例在t=0,3.53×10-2,7.98×10-2,1.18×10-1時的數值解Fig.1 Numerical solution of the case t=0,3.53×10-2,7.98×10-2,1.18×10-1

圖1顯示了在不同時間點上Allen-Cahn方程解的數值結果。結果表明,隨著時間增大,其形狀由初始時間t0的啞鈴狀不斷向圓形聚攏,數值結果與文獻[11]中的結果吻合。

3 結 語

本文應用快速離散余弦變換結合積分因子方法求解非線性Allen-Cahn方程。該方法能夠快速地將空間離散得到的非線性常微分方程組進行時間離散,得到方程的數值解,提高計算效率。通過求解齊次Neumann邊界條件下的非線性Allen-Cahn方程,可以發現隨時間推移數值結果形狀的變化規律。

附錄驗證定理1中,Bxyj=λjyj,j=0,1,…,Nx-1,其中λj=2-2cos(jπ/Nx),yj=(cosjπξ1,…,cosjπξNx)T,j=0,1,…,Nx-1,由網格中心點的定義ξi=(i-1/2)h,i=1,2,…,Nx,在左右各增加一個虛擬網格,其中心點坐標為ξ0=-h/2,ξNx+1=1+h/2。

利用和差化積公式cos(jπξi-1)=cos(jπξi)cos(jπ/Nx)+sin(jπξi)sin(jπ/Nx)和cos(jπξi+1)=cos(jπξi)cos(jπ/Nx)-sin(jπξi)sin(jπ/Nx),可得-cos(jπξi-1)+2cos(jπξi)-cos(jπξi+1)=(2-2cos(jπ/Nx))cos(jπξi)。因為cos(jπξ0)=cos(jπξ1),cos(jπξNx)=cos(jπξNx+1),于是cos(jπξ1)-cos(jπξ2)=-cos(jπξ0)+2cos(jπξ1)-cos(jπξ2)=(2-2cos(jπ/Nx))cos(jπξ1),-cos(jπξNx-1)+cos(jπξNx)=-cos(jπξNx-1)+2cos(jπξNx)-cos(jπξNx+1)=(2-2cos(jπ/Nx))cos(jπξNx)。

驗證完畢。