基于全復數型濾波器的三相鎖相環技術

何 宇 漆漢宏 鄧小龍

基于全復數型濾波器的三相鎖相環技術

何 宇1,2漆漢宏2鄧小龍1

（1. 江蘇信息職業技術學院智能工程學院 無錫 214153 2. 燕山大學電氣工程學院 秦皇島 066004）

近年來，前置復數濾波器（CCF）的鎖相環（PLL）技術成為電網同步研究中的熱點。然而，現有的CCF-PLL已被證實其數學模型和控制性能與傳統的實數濾波器型PLL基本一致。為提高系統的控制性能，該文提出一種CCF結構完全復數化的三相PLL技術。首先，給出前級濾波結構關于電壓的傳遞函數，驗證該結構可以準確分離出電網的基波正負序分量。其次，進行前級結構關于基波正序相位的數學建模，結合后級的同步旋轉坐標系PLL，構建整個PLL系統關于相位的數學模型，并利用三階最佳校正法對系統進行設計，確定相關控制參數。研究發現，若采用與CCF-PLL相同的開環截止頻率，所提PLL的中頻段寬度更寬、相位裕度更大。另外，還設計了多重全復數濾波結構級聯的三相PLL，以便更徹底地抑制電網諧波。最后，通過仿真和實驗進行驗證，結果表明，相比CCF-PLL，所提PLL的控制性能更佳。

鎖相環 復數濾波器 控制性能 相位裕度

0 引言

傳統能源（如煤、石油和天然氣等）的過度使用致使不可再生能源日趨枯竭；另外，采用傳統能源發電會造成環境污染和生態破壞等問題。所以，基于可再生綠色能源（如太陽能和風能等）的開發和利用備受關注[1]。采用并網逆變器將綠色能源發出的電能并入電網是一種行之有效的手段[2]。在逆變器的控制中，調節電網電壓和輸出電流之間的相位差[3]、實現并網逆變器的孤島檢測功能[4]和故障穿越功能[5-6]通常都要用到鎖相環（Phase Locked Loop, PLL）技術。因此，PLL技術已成為分布式發電系統并網運行的眾多關鍵技術之一[7]。

在三相PLL的研究中，技術比較成熟的有同步旋轉坐標系（Synchronous Rotating Frame, SRF）型PLL[8]、滑動平均濾波器（Moving Average Filter, MAF）型PLL[9-10]、自適應陷波器（Adaptive Notch Filter, ANF）型PLL[11-12]、雙二階廣義積分器（Double Second-Order Generalized Integrator, DSOGI）型PLL[13-14]和復數濾波器（Complex Coefficient Filter, CCF）型PLL[15-18]。其中，由文獻[15]提出的CCF技術由于控制結構簡單、濾波原理清晰等特點在三相PLL的研究中受到持續關注。該CCF結構在電網的基波正、負序分量（Fundamental Positive-and Negative-Sequence Components, FPSC/FNSC）處具有頻率極性的選擇性，無需對稱分量法即可分離出FPSC和FNSC。文獻[16]為改善并網電流質量，介紹了如何在三相靜止坐標系下直接使用CCF結構。文獻[17]提出了對高次諧波抑制能力更強的高階CCF控制方案。文獻[18]將重復控制的內模嵌入到CCF結構中，使PLL能夠完全濾除電網中的主要諧波。除PLL外，CCF結構在逆變器的電流控制[19]、鎖頻環[20]和電機控制[21]中也都得到了成功運用。

然而，上述相關文獻對CCF-PLL研究時，將前級的CCF結構和后級的SRF-PLL作為獨立系統對待，并分開進行了處理。文獻[22-24]指出，前置濾波器型PLL的前、后兩級是相互聯系的，不能看成分立系統。文獻[22-23]將前后兩級結合起來分析，對整個PLL系統進行了小信號數學建模，研究表明：CCF-PLL雖然結構簡單，但其數學模型與ANF-PLL、DSOGI-PLL等實數濾波器型PLL是一致的。文獻[23-24]通過對比實驗發現，CCF-PLL的控制性能與實數濾波器型PLL相比基本無異，并無突出優勢。

為提高CCF-PLL的控制性能，提出了一種將CCF結構進一步復數化的三相PLL技術。為充分發揮復數系統的優勢，將CCF所對應傳遞函數分子也改用復數表示。改進后的CCF結構不僅保持了正負頻率的選擇性，還提高了前級濾波結構的截止頻率，從而加大了整個PLL系統的中頻段寬度和相位裕度。仿真和對比實驗表明，所提PLL在保留CCF- PLL能順利分離FPSC/FNSC和精確鎖頻、鎖相的同時，顯著地提高了系統的控制性能。

1 提出的全復數型CCF結構

現有的CCF結構[15-21]如圖1所示。

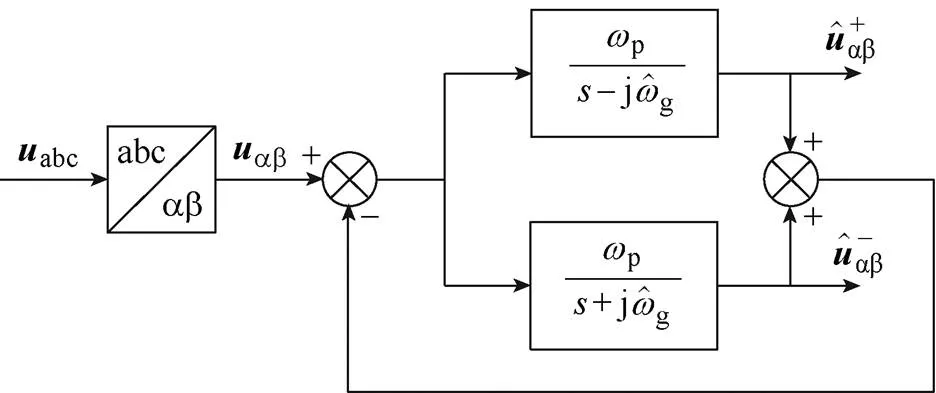
圖1 現有的CCF結構

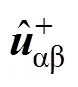
為改善控制性能，提出的全復數型濾波器（All Complex Coefficient Filter, ACCF）結構如圖2所示。

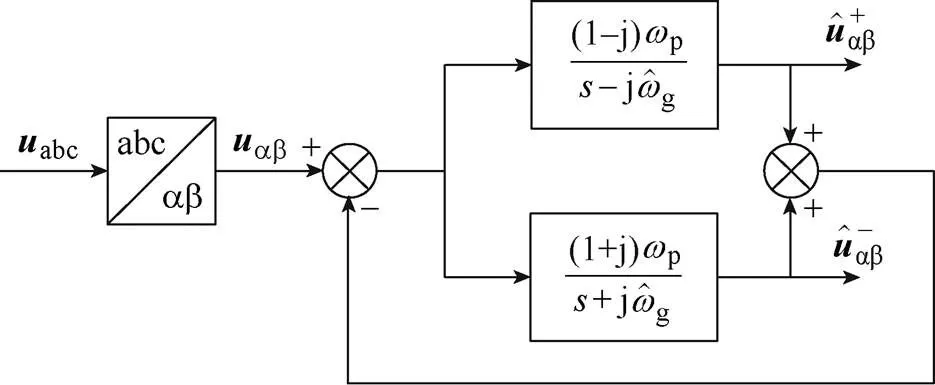
圖2 提出的ACCF結構

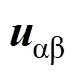
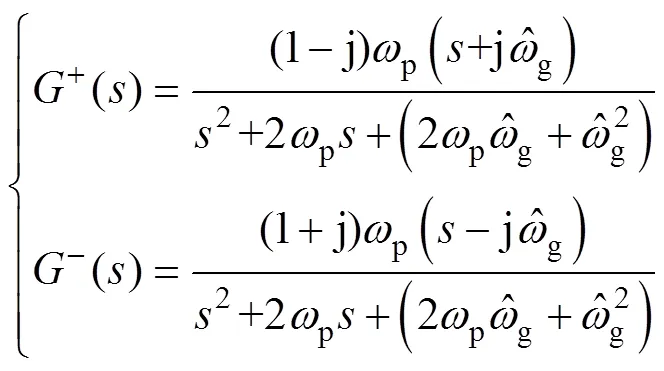
由式（1）可知，ACCF結構關于電壓是一個二階線性系統，其阻尼比和自然角頻率n滿足

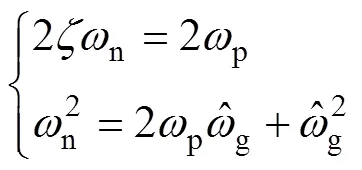
將式（2）中的n消去，可解得p為

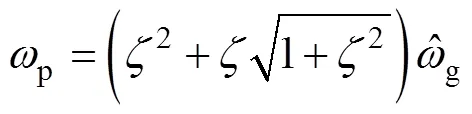
可見，相比CCF結構，ACCF結構的p有所增大；而p的大小直接影響整個PLL系統的中頻段寬度和相位裕度（具體參見2.3節），因此，p值的不同勢必會導致ACCF結構與CCF結構在PLL系統的控制性能上表現出不一樣的動態行為。

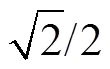
1.1 ACCF結構的正負序分離特性

由式（1）和圖3可得

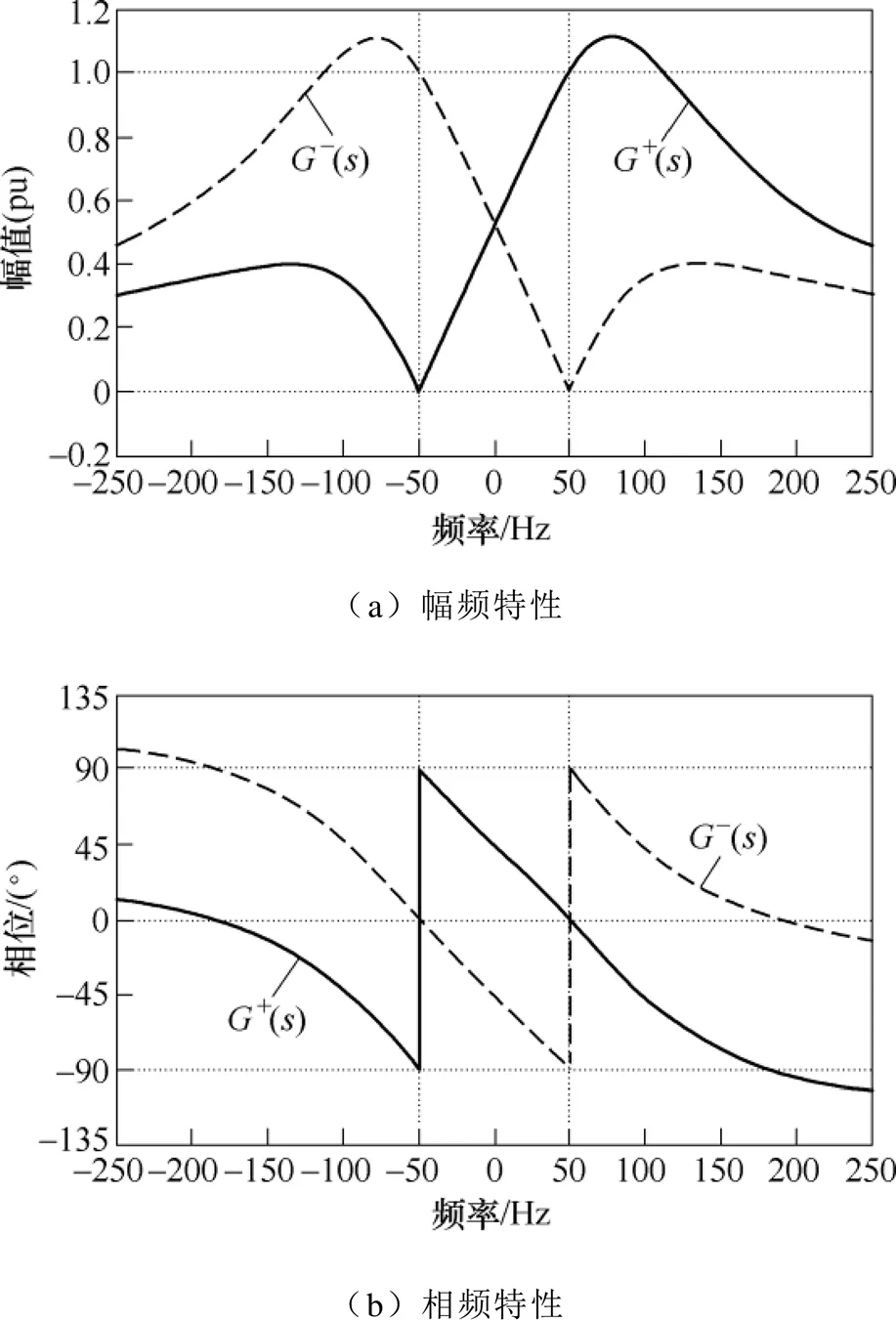
圖3 G+(s)和的頻率特性曲線

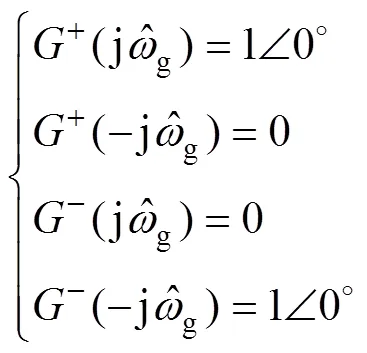
經典控制理論[25]指出，若角頻率為0的正弦信號經線性系統()作用后，其輸出信號的角頻率保持不變，而幅值是原信號的|(j0)|倍，相位會在原來的基礎上偏移∠(j0)。

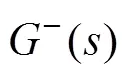
1.2 ACCF結構關于基波正序相位的數學模型

以上對正負序電壓的分析建立在ACCF結構關于電壓的數學模型之上，而PLL需要提取出FPSC的相位，所以還要對ACCF結構關于基波正序相位進行數學建模。

假設由ACCF結構分離出的FPSC和FNSC為

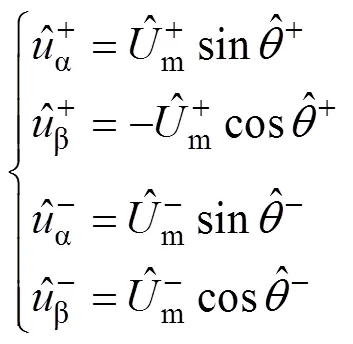
由式（5）可得

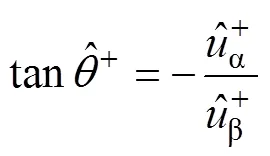
將式（6）兩端對時間求導，得

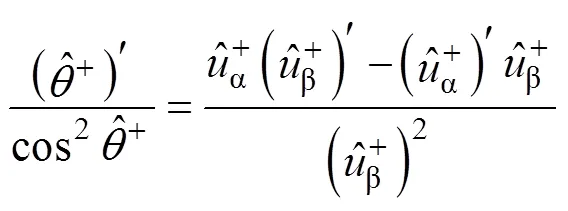
根據圖2，可得ACCF結構中正序濾波器的輸入、輸出關系為

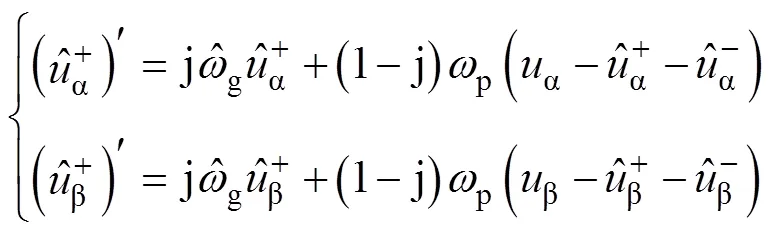
式中，ab的具體表達式為

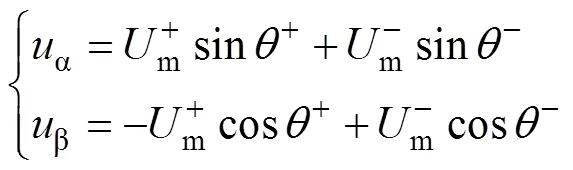
在三相電力系統的ab坐標系下，任一變量ab均滿足[16-18]：ja=-b，jb=a。因此，式（8）可進一步轉化為

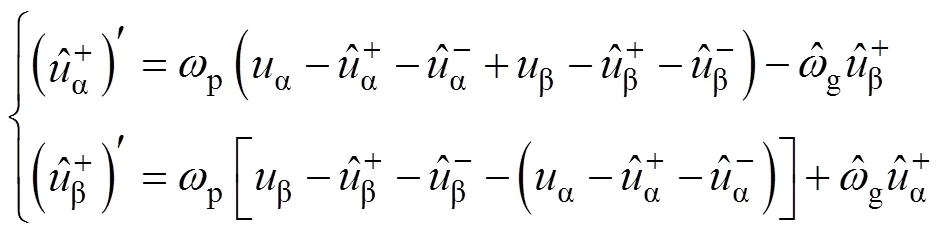
將式（5）、式（9）和式（10）代入到式（7）并化簡得

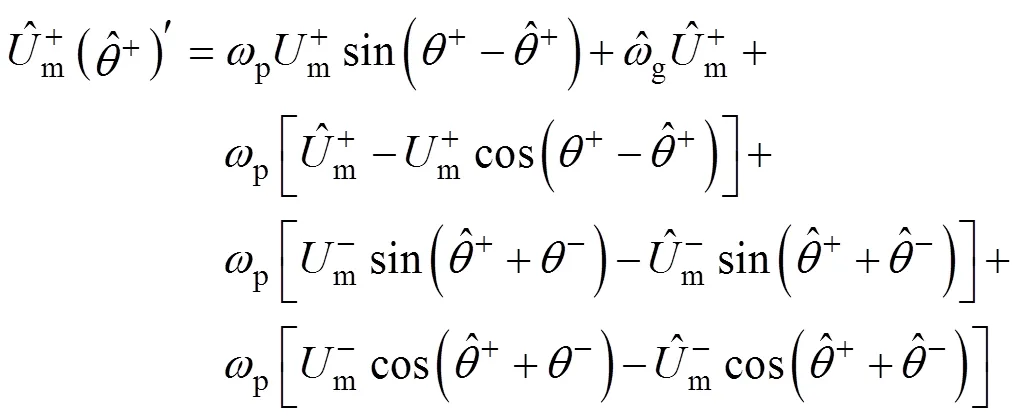
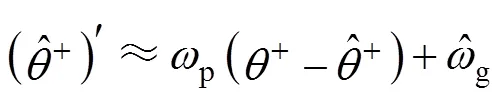
式（12）即為ACCF結構關于基波正序相位的時域數學模型，其復數域的數學模型如圖4所示。

2 前置ACCF結構的三相PLL

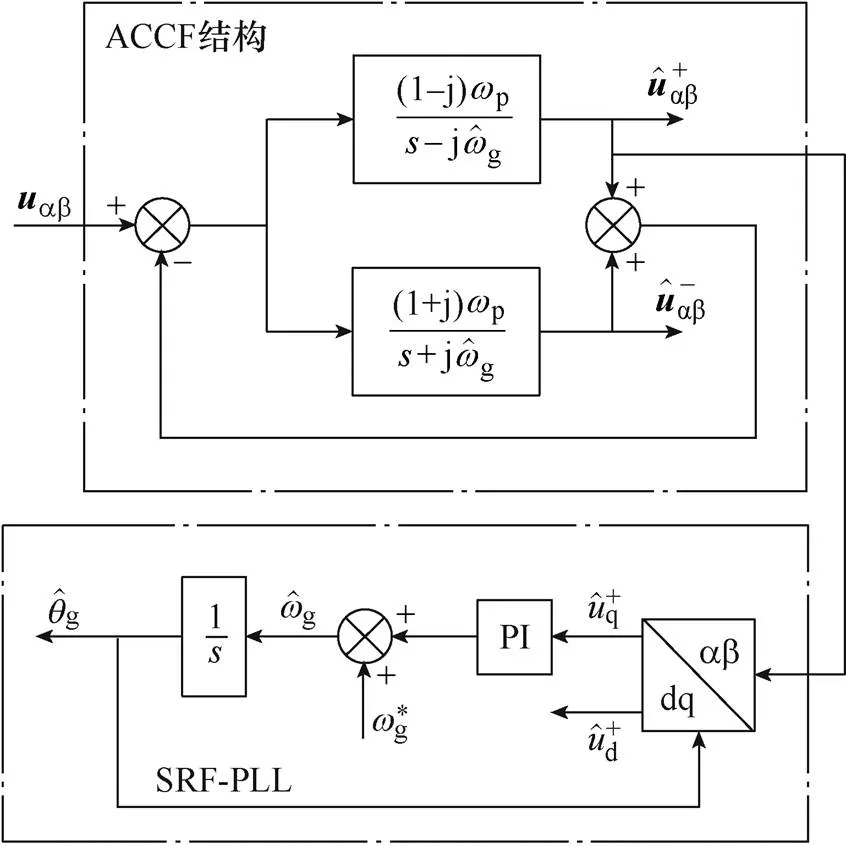
圖5 基于ACCF結構的三相PLL

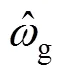
SRF-PLL在理想電網條件下的鎖頻和鎖相能力十分突出（其基本工作原理可參見文獻[8]），因此在畸變/不平衡電網環境中通常作為前置濾波器型PLL（如DSOGI-PLL、CCF-PLL等）的后級使用。該PLL關于相位的數學模型如圖6所示。圖中，p、i分別為PI控制器的比例和積分系數。

圖6 SRF-PLL關于相位的數學模型

2.1 ACCF-PLL關于基波正序相位的數學模型

將前后兩級關于基波正序相位的數學模型（見圖4和圖6）結合起來，可得整個PLL系統（見圖5）的數學模型如圖7所示。

圖7 ACCF-PLL關于基波正序相位的數學模型

根據梅森增益公式[25]，可得圖7對應控制系統的閉環傳遞函數為

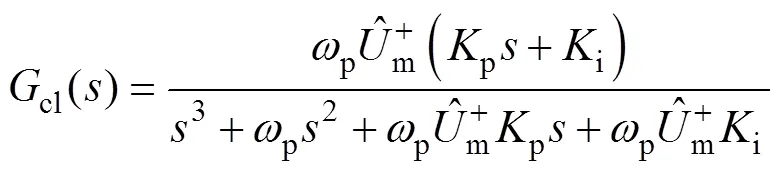
對控制系統進行分析和校正時，通常以其開環傳遞函數為研究對象。由式（13）可得，ACCF-PLL對應系統的等效開環傳遞函數為

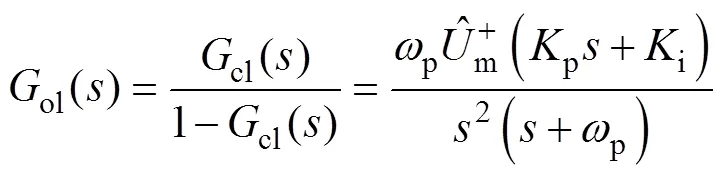
因此，ACCF-PLL的等效數學模型如圖8所示。

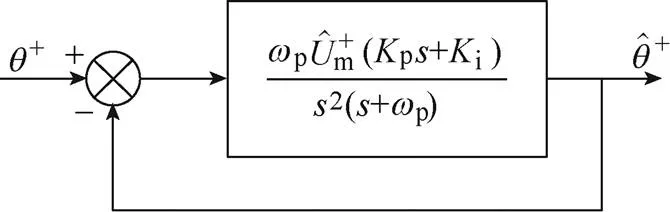
圖8 ACCF-PLL的等效數學模型

由圖8可知，該控制結構為Ⅱ型單位反饋系統，可以無靜差地跟蹤像電網相位這樣的斜坡輸入。

2.2 ACCF-PLL的系統校正與參數整定

由于ACCF-PLL為三階控制系統，可采用三階最佳設計法[23, 25]對其校正，期望的系統頻率特性曲線如圖9所示。圖中，c、分別為系統的開環截止頻率和相位裕度。

該設計法的主導思想是使控制系統取得最大的相位裕度，此時c為中頻段的幾何中心，即

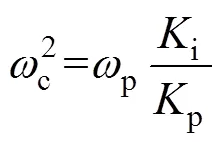
由式（14）可知，c滿足

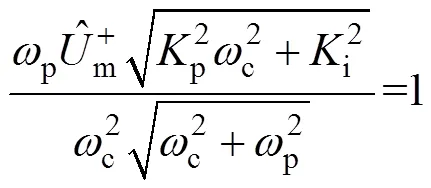
聯立式（15）和式（16）可解得

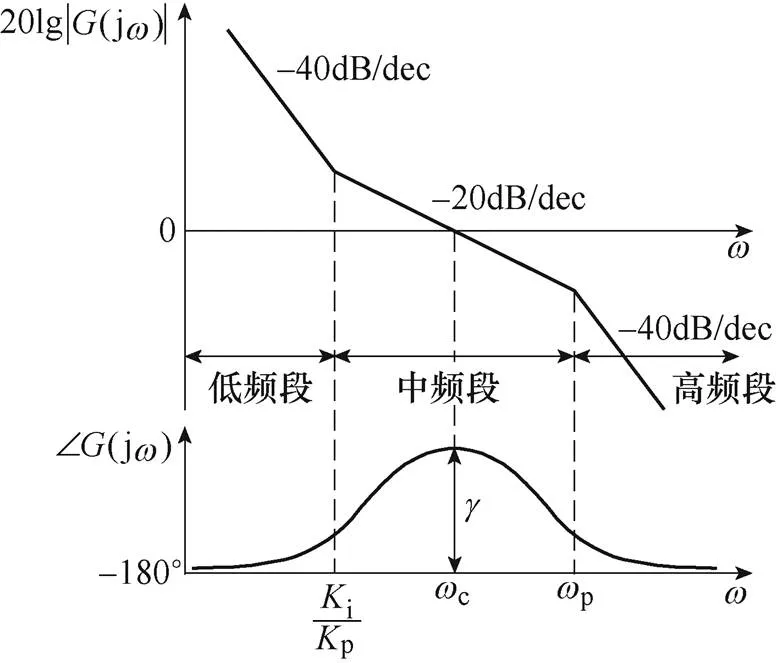
圖9 三階最佳設計法下系統的頻率特性曲線

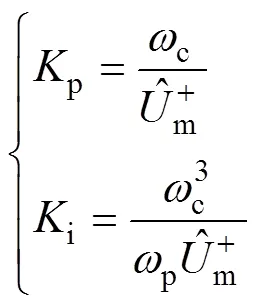
由圖9可知，c的值需小于p。若c靠近p，則系統的響應速度變快，但其中頻段寬度和相位裕度都會減小，輸出信號的超調量會增大，同時系統的濾波性能降低；若c遠離p，雖然系統的穩定性和抗干擾性增強，但其響應速度變慢。所以，c的取值要兼顧系統的快速性、超調量和濾波性能。文獻[23-24]通過研究分析和論證，推薦c的取值區間為40p～50prad/s，本文取c=45prad/s。將c= 141.37rad/s、p=429.15rad/s代入式（17）可得

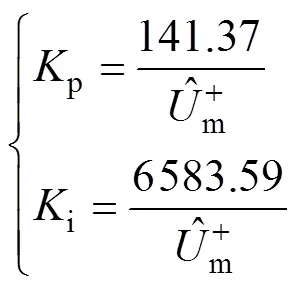
根據電網電壓的幅值，由式（18）即可求出PI控制器的參數p和i。

2.3 CCF-PLL與ACCF-PLL的動態性能比較

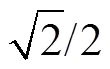
圖10中，p0為CCF-PLL前級濾波結構的截止角頻率；p0、i0分別為CCF-PLL中PI控制器的比例項和積分項系數；0、分別為CCF-PLL和ACCF-PLL對應控制系統的中頻段寬度。由圖10可得

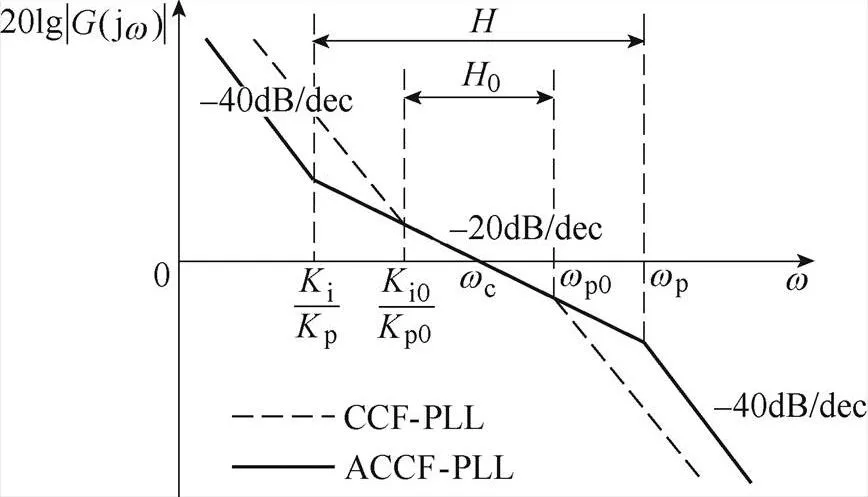
圖10 CCF-PLL和ACCF-PLL的幅頻特性曲線

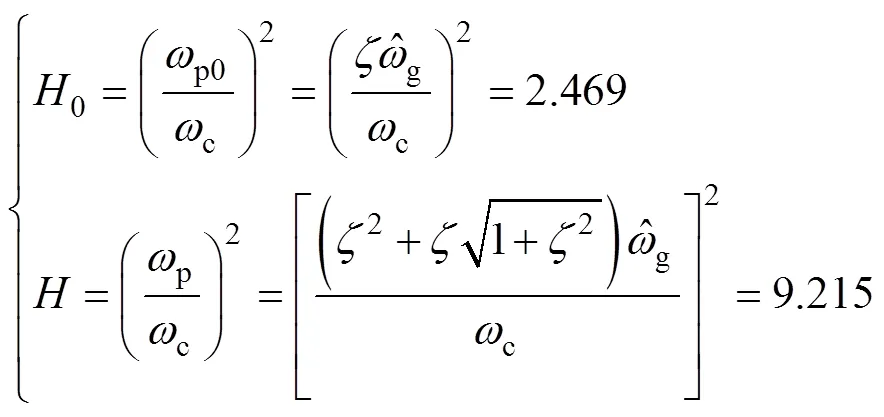
根據相位裕度和中頻段寬度的關系[25]，可得

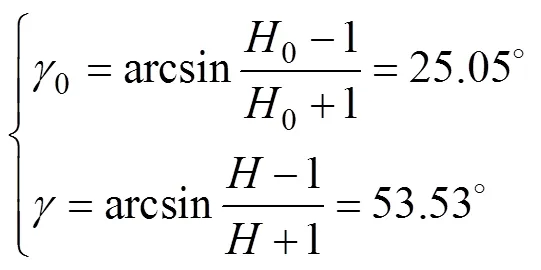
式中，0為CCF-PLL的系統相位裕度。

圖11給出了CCF-PLL和ACCF-PLL對應控制系統的Bode圖。經典控制理論[25]指出，要使控制系統有一個良好的動態調節過程，其相位裕度要達到45°～70°。若相位裕度過低于此范圍，系統的動態性能較差，對參數變化較敏感；過高于此范圍，系統的穩定程度過好，動態過程會變得很緩慢。由式（20）和圖11可知，ACCF-PLL的相位裕度處于上述范圍內，而CCF-PLL的相位裕度過低。因此，ACCF-PLL勢必會展現出比CCF-PLL更好的動態 性能。

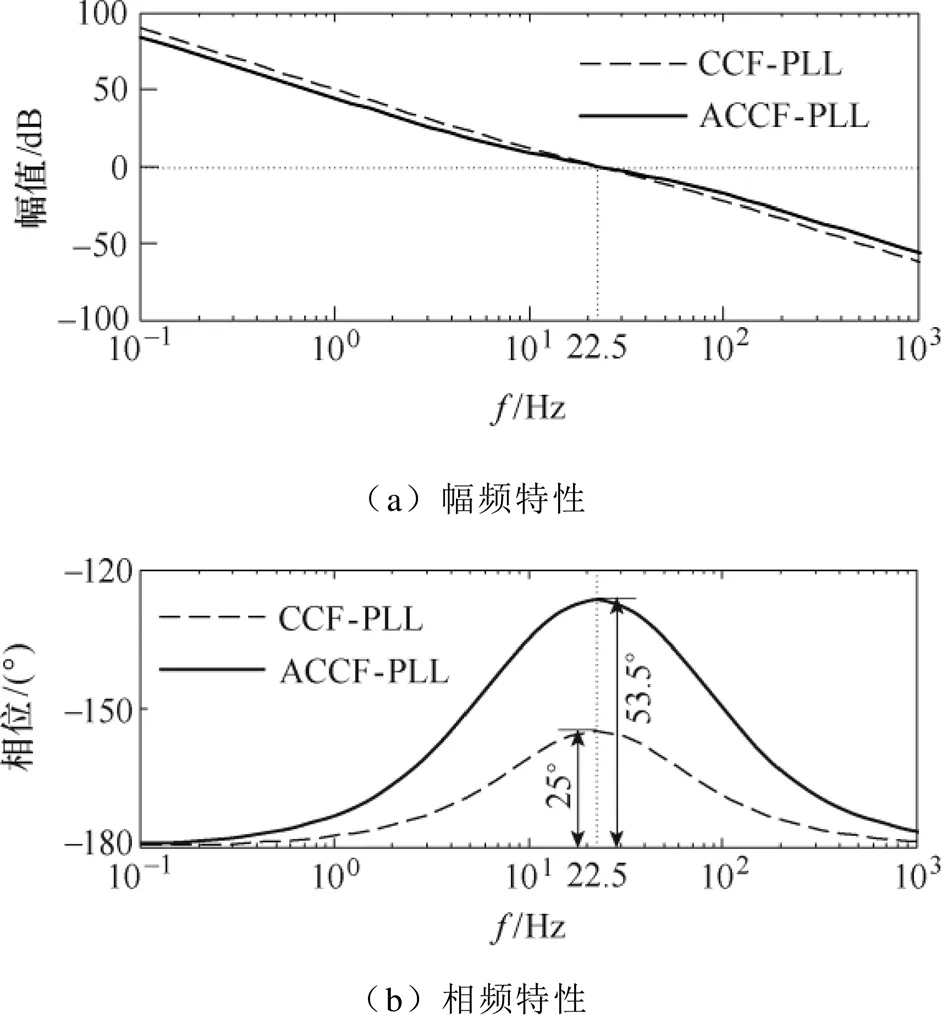
圖11 CCF-PLL和ACCF-PLL的Bode圖

2.4 多重ACCF結構的三相PLL

電網電壓除存在基波負序外，還會受到諧波污染[26]。ACCF-PLL經上述設計法校正后雖對諧波有一定的抑制能力，但無法將諧波完全濾除。為此，本文仿照多重CCF（Multiple CCF, MCCF）型PLL[15]的架構，設計了如圖12所示的基于多重ACCF（Multiple ACCF, MACCF）結構的三相PLL。

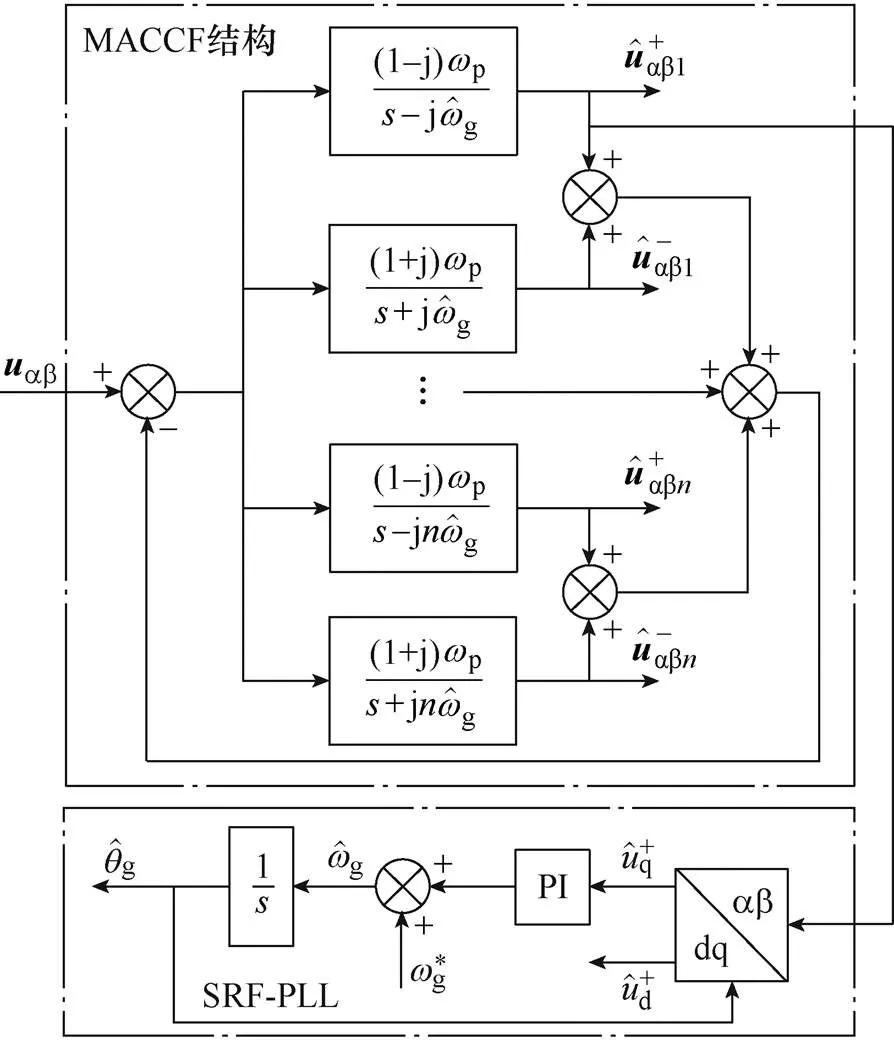
圖12 基于MACCF結構的三相PLL

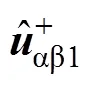
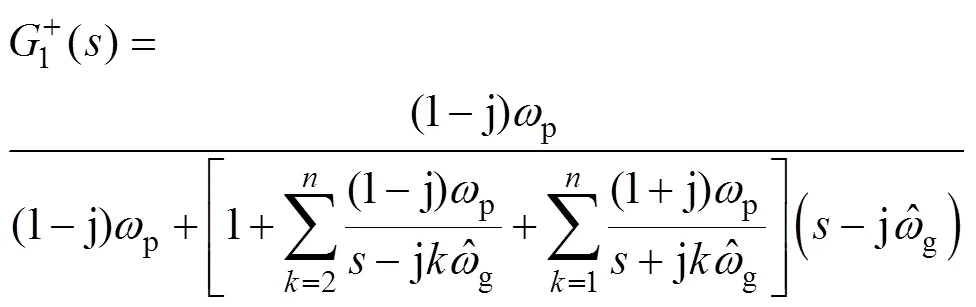
根據式（21），容易求得

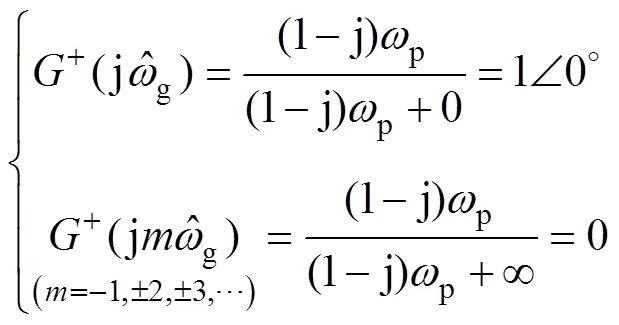
在實際電網的諧波中，主要以低次（-5次和+7次）諧波為主，高次諧波含量很小[26]。因此，在實際應用MACCF-PLL時，只要在MACCF結構中配置主要的濾波模塊即可，而不必過多羅列。

2.5 數字實現

本文1.2節中已提及：在ab坐標系下，任一變量ab均滿足：ja=-b，jb=a。故ACCF結構中正負序濾波器的實現方法如圖13所示。圖中，ab、ab分別為復數濾波器的輸入和輸出信號。

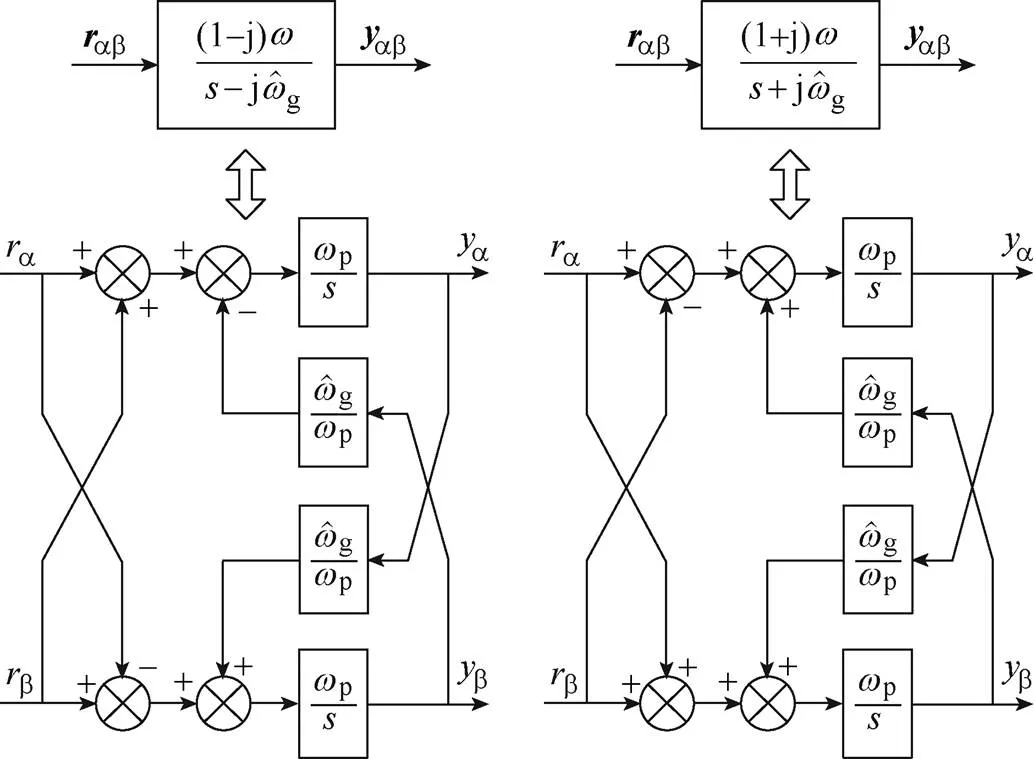
圖13 全復數型濾波器的實現方法

為確保離散精度和避免出現代數環，這里采用三階Adams-Bashforth算法[15, 17]對圖13和后級PI控制器及積分器中的拉普拉斯算子進行離散化，具體的數字離散化算法為

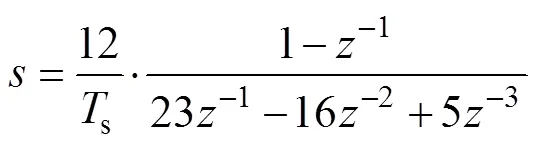
式中，s為采樣周期。

3 仿真驗證

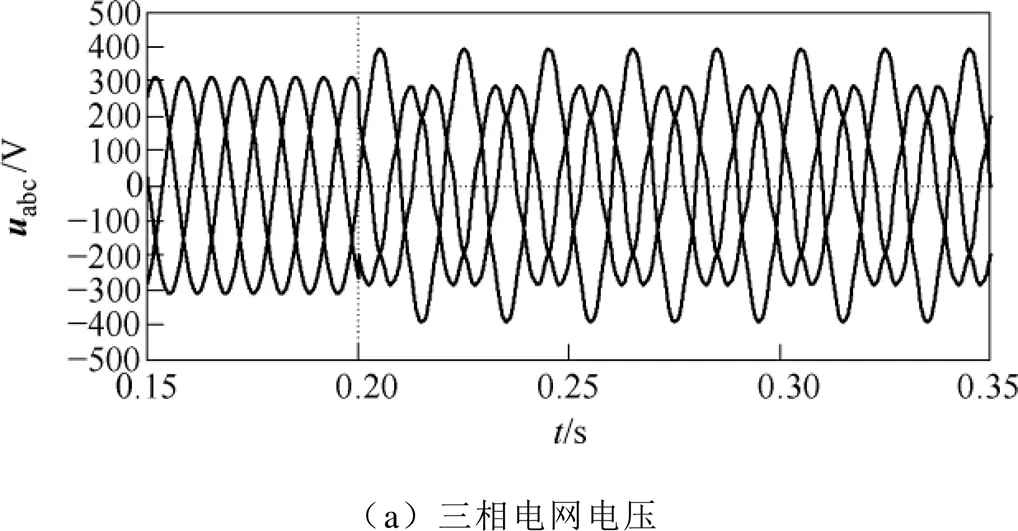
正負序分離方面：由圖14b～圖14d可知，分離出的FPSC除在電網突然變化的極短時間內有略微抖動外，其余時間均未發生變化，其幅值保持在1(pu)；分離出的FNSC在電網變化后開始出現，其幅值在半個理想電網周期（0.01s）內即由0上升并收斂于0.25(pu)。可見，提出的ACCF-PLL具備迅速、準確的正負序分離能力。

鎖頻方面：圖15c給出了捕獲頻率的動態響應過程，具體表現為提取的頻率在電網變化后由50Hz開始快速追蹤，并最終以55Hz為基準作衰減收斂，該過程的動態調節時間為44ms。因此，ACCF-PLL能在較短時間內無靜差地鎖住頻率。

4 實驗驗證

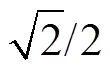
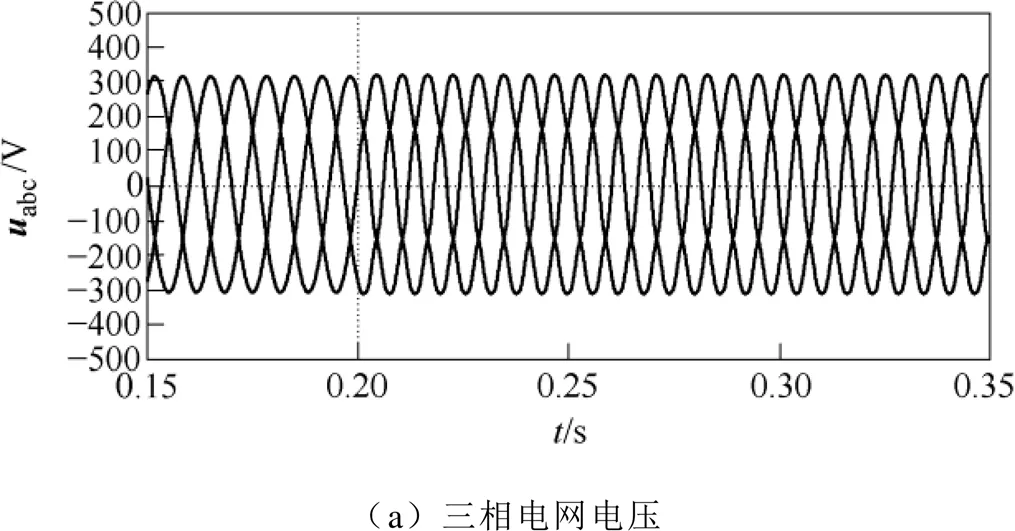
穩態性能上：在這兩種畸變/不平衡的電網測試環境中，ACCF-PLL都能成功提取出電網的FPSC/ FNSC（見圖16b和圖17b）、相位（見圖16c和圖17c）和頻率（見圖16d和圖17d）。由FPSC/FNSC的幅值曲線（見圖16c和圖17c）、頻率響應曲線（見圖16d和圖17d）和相位誤差曲線（見圖16d和圖17d）可以看到，這些變量都能無波動地穩定在初始值（或0）和無偏差地跟蹤預設的變化值，說明所設計的ACCF-PLL是一個穩定的無靜差控制系統，能夠精確進行基波正負序分離、鎖頻和鎖相。

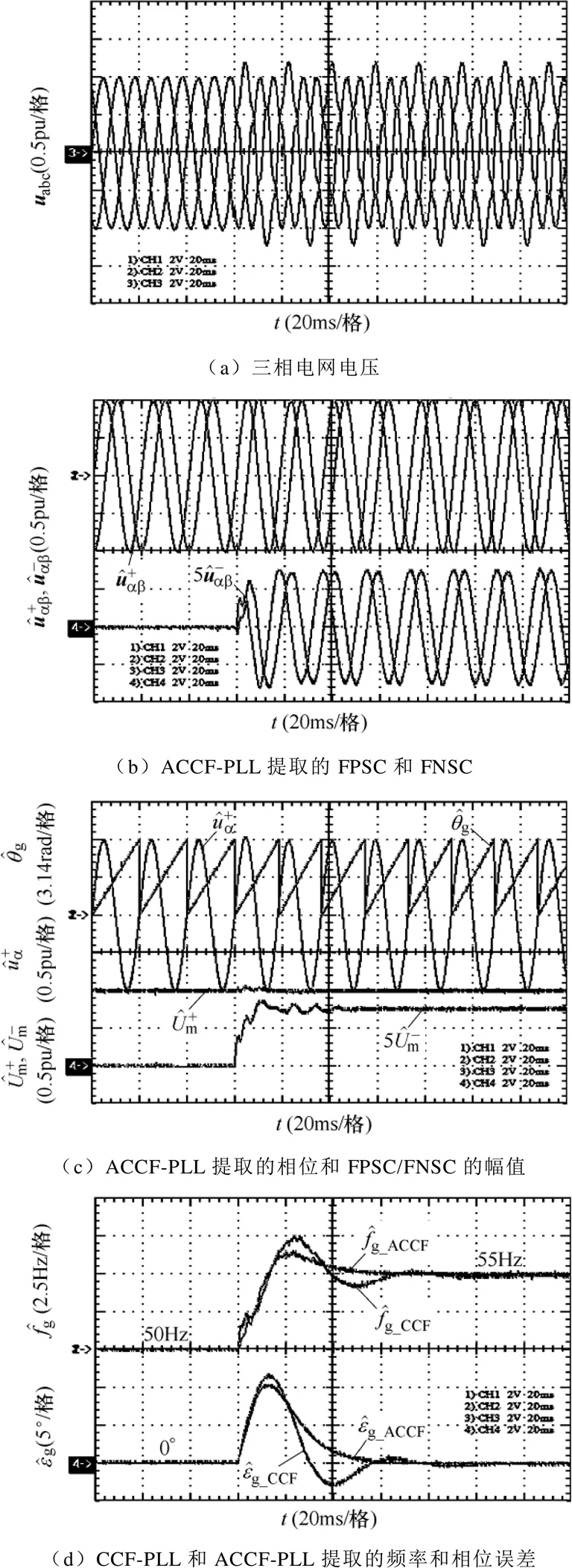
圖16 頻率突變+5Hz下的實驗結果

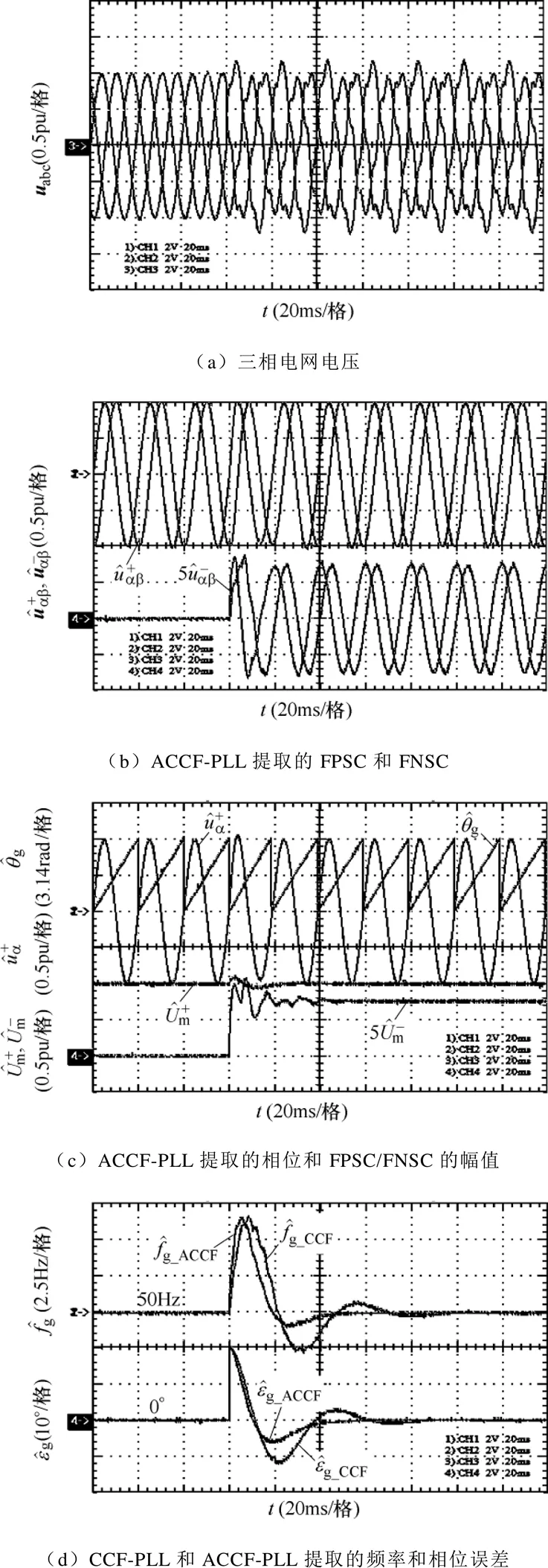
圖17 相位跳變+20°下的實驗結果

動態性能上：圖16d和圖17d展示了CCF-PLL和ACCF-PLL在提取電網頻率及相位誤差上的對比結果。表1根據實驗數據給出了兩者具體的動態指標值。可見，ACCF-PLL在動態收斂過程中表現出的衰減程度和速度都要大于CCF-PLL；產生的頻率超調和相位誤差超調要小于CCF-PLL，尤其是第二次離開穩態值的反向超調要比CCF-PLL小很多；兩種PLL雖看似有相近的調節時間，但ACCF-PLL進入終值誤差帶的時刻要早于CCF-PLL，響應速度更快。綜上，ACCF-PLL呈現出的動態行為要優于CCF-PLL。

表1 CCF-PLL和ACCF-PLL的動態指標值

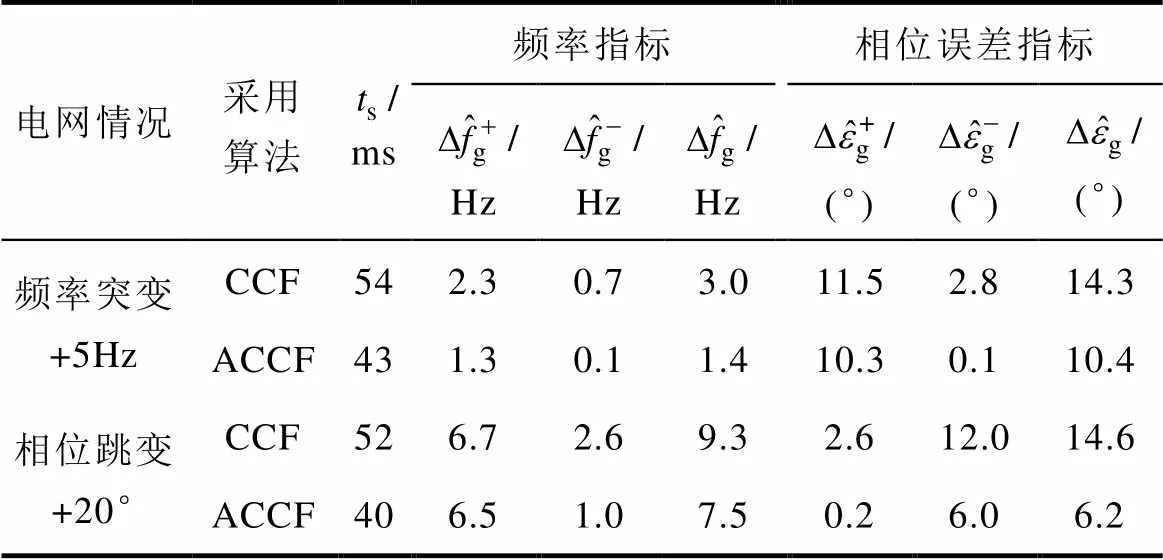
Tab.1 The dynamic index ofCCF-PLL and ACCF-PLL

抗干擾性能上：由圖16a和圖17a可以看出，測試PLL的電網環境是較為惡劣的，但兩種PLL提取的各信號在穩態時不存在諧波或波動，即PLL完全抑制了所加入的各次諧波。因此，CCF-PLL和ACCF-PLL都具備較強的抗干擾能力。

5 結論

為改進PLL的控制性能，在CCF-PLL的基礎上，提出了一種將前級CCF結構全面復數化的三相PLL技術，即ACCF-PLL算法。通過理論分析、仿真驗證和對比實驗，得出如下結論：

1）ACCF結構保持了CCF結構控制原理簡單的優勢，在FPSC和FNSC處具有正負頻率的選擇性，無需對稱分量法即可分離出FPSC和FNSC。

2）相比CCF結構，ACCF結構提高了其截止頻率，從而能夠拉寬整個PLL系統的中頻段寬度。

3）若CCF-PLL和ACCF-PLL的前級濾波結構選用相同的阻尼比，且整個控制系統采用一致的開環截止頻率，經三階最佳設計法校正后，ACCF-PLL的相位裕度明顯優于CCF-PLL。

4）在電網頻率、相位和負序突變時，ACCF-PLL都能準確進行基波正負序分離、鎖頻和鎖相；測得的頻率和相位誤差超調量要小于CCF-PLL，系統響應速度也快于后者。因此，ACCF-PLL表現出的動態性能更優異。

5）在畸變電網環境下，ACCF結構中配置的濾波模塊能完全消除電網諧波對系統輸出的影響。

[1] Tezer T, Yaman R, Yaman G. Evaluation of approaches used for optimization of stand-alone hybrid renewable energy systems[J]. Renewable and Sustainable Energy Reviews, 2017, 73: 840-853.

[2] 涂春鳴, 高家元, 趙晉斌, 等. 弱電網下具有定穩定裕度的并網逆變器阻抗重塑分析與設計[J]. 電工技術學報, 2020, 35(6): 1327-1335.

Tu Chunming, Gao Jiayuan, Zhao Jinbin, et al. Analysis and design of grid-connected inverter impedance remodeling with fixed stability margin in weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1327-1335.

[3] Castelló J, Espí J M, García-gil R. A new generalized robust predictive current control for grid-connected inverters compensates anti-aliasing filters delay[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4485-4494.

[4] 王曉寰, 張旭東, 郭紅強. 基于相位簇擾動的下垂控制并網逆變器孤島檢測[J]. 電工技術學報, 2020, 35(8): 1728-1738.

Wang Xiaohuan, Zhang Xudong, Guo Hongqiang. Islanding detection of droop-controlled grid-connected inverters on phase cluster disturbance[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1728- 1738.

[5] Guo Xiaoqiang, Liu Wenzhao, Lu Zhigang. Flexible power regulation and current-limited control of the grid-connected inverter under unbalanced grid voltage faults[J]. IEEE Transactions on Industrial Electronics, 2017, 64(9): 7425-7432.

[6] 涂春鳴, 葛欽, 肖凡, 等. 基于光伏電源支撐的多端口固態變壓器故障穿越策略[J]. 電工技術學報, 2020, 35(16): 3498-3508.

Tu Chunming, Ge Qin, Xiao Fan, et al. Fault ride- through control strategy of solid state transformer with PV power generation[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3498-3508.

[7] 何宇, 漆漢宏, 羅琦, 等. 基于分數階濾波器的三相鎖相環技術[J]. 電工技術學報, 2019, 34(12): 2572-2583.

He Yu, Qi Hanhong, Luo Qi, et al. A novel three- phase phase-locked loop method based on fractional- order filter[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2572-2583.

[8] Hans F, Schumacher W, Harnefors L. Small-signal modeling of three-phase synchronous reference frame phase-locked loops[J]. IEEE Transactions on Power Electronics, 2018, 33(7): 5556-5560.

[9] Golestan S, Guerrero J M, Vidal A, et al. PLL with MAF-based prefiltering stage: small-signal modeling and performance enhancement[J]. IEEE Transactions on Power Electronics, 2016, 31(6): 4013-4019.

[10] Li Haoyuan, Zhang Xing, Xu Chengjun, et al. Sensorless control of IPMSM using moving-average- filter based PLL on HF pulsating signal injection method[J]. IEEE Transactions on Energy Conversion, 2020, 35(1): 43-52.

[11] Lee K J, Lee J P, Shin D, et al. A novel grid synchronization PLL method based on adaptive low-pass notch filter for grid-connected PCS[J]. IEEE Transactions on Industrial Electronics, 2014, 61(1): 292-301.

[12] 張國強, 王高林, 徐殿國, 等. 基于自適應陷波濾波器的內置式永磁電機轉子位置觀測方法[J]. 中國電機工程學報, 2016, 36(9): 2521-2527.

Zhang Guoqiang, Wang Gaolin, Xu Dianguo, et al. Adaptive notch filter based rotor position estimation for interior permanent magnet synchronous motors[J]. Proceedings of the CSEE, 2016, 36(9): 2521-2527.

[13] 楊才偉, 王劍, 游小杰, 等. 二階廣義積分器鎖頻環數字實現準確性對比[J]. 電工技術學報, 2019, 34(12): 2584-2596.

Yang Caiwei, Wang Jian, You Xiaojie, et al. Accuracy comparison of digital implementation on the second-order generalized integrator frequency- locked loop[J]. Transactions of China Electro- technical Society, 2019, 34(12): 2584-2596.

[14] Chen Ke, Ai Wu, Chen Bing, et al. Measuring and reconstruction algorithm based on improved second- order generalised integrator configured as a quadrature signal generator and phase locked loop for the three- phase AC signals of independent power generation systems[J]. IET Power Electronics, 2016, 9(11): 2155-2161.

[15] Guo Xiaoqiang, Wu Weiyang, Chen Zhe. Multiple- complex coefficient-filter-based phase-locked loop and synchronization technique for three-phase grid- interfaced converters in distributed utility networks[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1194-1204.

[16] Guo Xiaoqiang, Guerrero J M. Abc-frame complex- coefficient filter and controller based current harmonic elimination strategy for three-phase grid connected inverter[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(1): 87-93.

[17] Li Weiwei, Ruan Xinbo, Bao Chenlei, et al. Grid synchronization systems of three-phase grid- connected power converters: a complex-vector-filter perspective[J]. IEEE Transactions on Industrial Electronics, 2014, 61(4): 1855-1870.

[18] 何宇, 漆漢宏, 鄧超, 等. 一種嵌入重復控制內模的三相鎖相環的設計與實現[J]. 電工技術學報, 2016, 31(22): 83-91.

He Yu, Qi Hanhong, Deng Chao, et al. A novel three-phase phase-locked loop method based on internal model of repetitive control[J]. Transactions of China Electrotechnical Society, 2016, 31(22): 83-91.

[19] Busada C, Jorge S G, Leon A E, et al. Current controller based on reduced order generalized integrators for distributed generation systems[J]. IEEE Transactions on Industrial Electronics, 2012, 59(7): 2898-2909.

[20] Guest E, Mijatovic N. Discrete-time complex band- pass filters for three-phase converter systems[J]. IEEE Transactions on Industrial Electronics, 2019, 66(6): 4650-4660.

[21] An Quntao, Zhang Jianqiu, An Qi, et al. Frequency- adaptive complex-coefficient filter-based enhanced sliding mode observer for sensorless control of permanent magnet synchronous motor drives[J]. IEEE Transactions on Industry Applications, 2020, 56(1): 335-343.

[22] Ramezani M, Golestan S, Li S, et al. A simple approach to enhance the performance of complex- coefficient filter-based PLL in grid-connected appli- cations[J]. IEEE Transactions on Industrial Electro- nics, 2018, 65(6): 5081-5085.

[23] Golestan S, Monfared M, Freijedo F D. Design- oriented study of advanced synchronous reference frame phase-locked loops[J]. IEEE Transactions on Power Electronics, 2013, 28(2): 765-778.

[24] Golestan S, Monfared M, Freijedo F D, et al. Performance improvement of a prefiltered synchronous- reference-frame PLL by using a PID-type loop filter[J]. IEEE Transactions on Industrial Electronics, 2014, 61(7): 3469-3479.

[25] 胡壽松. 自動控制原理[M]. 6版. 北京: 科學出版社, 2013.

[26] Ahmed H, Bierhoff M, Benbouzid M, et al. Multiple nonlinear harmonic oscillator-based frequency esti- mation for distorted grid voltage[J]. IEEE Transa- ctions on Instrumentation and Measurement, 2020, 69(6): 2817-2825.

[27] 曲濤, 任元, 林海雪, 等. GB/T 14549-1993電能質量—公用電網諧波[S]. 中華人民共和國國家標準, 1993.

A Three-Phase Phase-Locked Loop Technique Based on All Complex Coefficient Filter

1,221

（1. School of Intelligent Engineering Jiangsu Vocational College of Information Technology Wuxi 214153 China 2. School of Electrical Engineering Yanshan University Qinhuangdao 066004 China）

Recently, the complex-coefficient-filter (CCF)-based phase-locked loop (PLL) technique has become a hotspot in grid synchronization research. However, the mathematical model and control performance of the current CCF-PLL have been confirmed to be basically consistent with the traditional real coefficient filter PLL. In order to improve the control performance, a novel three-phase PLL based on all complex coefficient filter is put forward. Firstly, the voltage transfer function of the pre-stage filter structure is given, and it is demonstrated that the structure can accurately separate the fundamental positive- and negative-sequence components. Then, the mathematical model of the pre-stage structure on the fundamental positive-sequence phase is derived. Combined with the post-stage synchronous rotating frame PLL, the mathematical model of the entire PLL system is built, and then the system is designed by the third-order optimum correction method. Wherein, the related control parameters are determined. It is shown that with the same open-loop cut-off frequency, the proposed PLL has a wider mid-frequency band width and a larger phase margin than the CCF-PLL. In addition, a multiple all-complex-coefficient-filter based PLL is designed to thoroughly eliminate harmonics. Finally, simulation and experimental results show that the control performance of the proposed PLL is better than that of the CCF-PLL.

Phase-locked loop, complex coefficient filter, control performance, phase margin

TM464

10.19595/j.cnki.1000-6753.tces.L90095

江蘇省高等學校自然科學研究項目（19KJB460028, 20KJB520021）、江蘇省高等學校優秀科技創新團隊項目（2019SJK07）和江蘇信息職業技術學院2020年重點科研課題項目（JSITKY202008）資助。

2020-06-22

2020-10-22

何 宇 男，1989年生，碩士，講師，研究方向為電力電子功率變換與控制、新能源發電技術。E-mail: galuohua@163.com

漆漢宏 男，1968年生，博士，教授，博士生導師，研究方向為電力電子功率變換與控制、新能源發電技術。E-mail: hhqi@ysu.edu.cn（通信作者）

（編輯 陳 誠）