單軸旋轉(zhuǎn)捷聯(lián)慣導(dǎo)系統(tǒng)圓錐誤差分析與仿真

丁 鵬，程向紅，劉文倩

（1.微慣性儀表與先進(jìn)導(dǎo)航技術(shù)教育部重點(diǎn)實(shí)驗(yàn)室，南京210096；2.東南大學(xué) 儀器科學(xué)與工程學(xué)院，南京 210096）

在捷聯(lián)式慣性導(dǎo)航系統(tǒng)(Strapdown Inertial Navigation Systems,SINS)中，陀螺儀直接固連于載體，敏感載體相對(duì)慣性空間的角運(yùn)動(dòng)。姿態(tài)算法的性能直接影響SINS 的導(dǎo)航精度，由于有限轉(zhuǎn)動(dòng)的不可交換性影響，姿態(tài)解算中不可避免地引入圓錐誤差，尤其是在高動(dòng)態(tài)環(huán)境下更為惡劣[1]。1971年Bortz 最早提出了等效旋轉(zhuǎn)矢量概念，在理論上解決了不可交換性誤差的補(bǔ)償問題，后續(xù)眾多學(xué)者在其基礎(chǔ)上對(duì)圓錐誤差補(bǔ)償算法進(jìn)行了研究[2-5]。

慣性測(cè)量單元(Inertial measurement unit,IMU)的測(cè)量精度是影響SINS 導(dǎo)航性能的主要因素，通過旋轉(zhuǎn)調(diào)制技術(shù)在SINS 上加裝一個(gè)轉(zhuǎn)位機(jī)構(gòu)，令I(lǐng)MU 按設(shè)計(jì)的方案進(jìn)行旋轉(zhuǎn)，通過旋轉(zhuǎn)調(diào)制可有效抑制IMU的常值誤差項(xiàng)，提高導(dǎo)航系統(tǒng)的精度[6]。雖然IMU 與載體之間不再直接固連，增加了轉(zhuǎn)位機(jī)構(gòu)和測(cè)角裝置，但在導(dǎo)航解算上仍采用捷聯(lián)慣導(dǎo)算法，因此也被稱為旋轉(zhuǎn)調(diào)制式捷聯(lián)慣導(dǎo)系統(tǒng)(Rotational Strapdown Inertial Navigation Systems,RINS)[7]。20 世紀(jì)90年代，Sperry 公司研制出首臺(tái)激光陀螺單軸旋轉(zhuǎn)慣導(dǎo)系統(tǒng)，并成功應(yīng)用于水面艦船和潛艇中[7]。后續(xù)國內(nèi)外研究團(tuán)隊(duì)開展了基于激光陀螺和光纖陀螺的單軸、雙軸和三軸旋轉(zhuǎn)慣導(dǎo)系統(tǒng)的研制[8,9]。

在單軸RINS 中，IMU 安裝在轉(zhuǎn)位機(jī)構(gòu)上并隨之轉(zhuǎn)動(dòng)，相對(duì)純SINS 其運(yùn)動(dòng)模型發(fā)生了改變，其不可交換性誤差、圓錐誤差補(bǔ)償效果以及補(bǔ)償后的剩余誤差也將發(fā)生改變，目前尚未有針對(duì)單軸RINS 此方面的研究。針對(duì)上述轉(zhuǎn)變，本文首先剖析了單軸RINS在典型圓錐環(huán)境下的運(yùn)動(dòng)形式，建立其運(yùn)動(dòng)模型并推導(dǎo)角速率擬合下的不可交換性誤差，然后研究了基于角速率的旋轉(zhuǎn)矢量算法和轉(zhuǎn)位方案對(duì)圓錐誤差補(bǔ)償?shù)挠绊懀詈笸ㄟ^仿真實(shí)驗(yàn)驗(yàn)證理論分析的有效性。

1 單軸旋轉(zhuǎn)捷聯(lián)慣導(dǎo)圓錐運(yùn)動(dòng)特性分析

相對(duì)于SINS，單軸RINS 的圓錐運(yùn)動(dòng)模型和不可交換性誤差均發(fā)生了改變，因此需要對(duì)其進(jìn)行分析推導(dǎo)，為圓錐誤差補(bǔ)償算法在實(shí)際工程中應(yīng)用提供參考。下面將以光纖陀螺慣導(dǎo)系統(tǒng)為例分析單軸RINS 的圓錐誤差，所得的結(jié)論同樣適用于輸出信號(hào)為角增量的激光陀螺系統(tǒng)。

1.1 單軸旋轉(zhuǎn)捷聯(lián)系統(tǒng)圓錐運(yùn)動(dòng)描述

圓錐運(yùn)動(dòng)是慣性儀表感受到角振動(dòng)的作用結(jié)果，當(dāng)其兩個(gè)正交軸上有同頻不同相的正弦角振動(dòng)輸入時(shí)，第三個(gè)正交軸上便會(huì)輸出常值角速度，稱為等效陀螺漂移，它的產(chǎn)生會(huì)帶來導(dǎo)航計(jì)算誤差，即圓錐誤差[1]。

本文所用的坐標(biāo)系定義：導(dǎo)航坐標(biāo)系n采用東-北-天地理坐標(biāo)系；載體坐標(biāo)系b按右-前-上構(gòu)成右手直角坐標(biāo)系；旋轉(zhuǎn)坐標(biāo)系r是三軸陀螺加速度計(jì)所指向的坐標(biāo)系，因此在轉(zhuǎn)位機(jī)構(gòu)旋轉(zhuǎn)起始時(shí)刻有。

在SINS 中，假設(shè)b系相對(duì)n系以為錐軸做典型圓錐運(yùn)動(dòng)，半錐角為α，圓錐運(yùn)動(dòng)角頻率為則SINS 中t時(shí)刻的姿態(tài)四元數(shù)為：

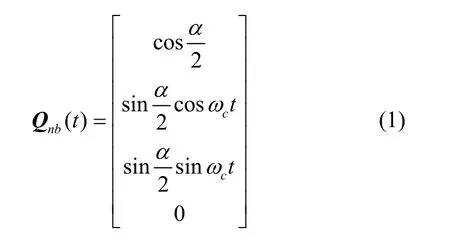
在單軸RINS 中IMU 安裝在一個(gè)轉(zhuǎn)位機(jī)構(gòu)上，由于轉(zhuǎn)位機(jī)構(gòu)相對(duì)載體坐標(biāo)系b存在轉(zhuǎn)動(dòng)，導(dǎo)致r系相對(duì)n系除了做典型圓錐運(yùn)動(dòng)外，還會(huì)隨著轉(zhuǎn)位機(jī)構(gòu)繞轉(zhuǎn)動(dòng)，設(shè)其轉(zhuǎn)速為則單軸RINS 中的圓錐運(yùn)動(dòng)可以表示為b系相對(duì)n系做圓錐運(yùn)動(dòng)與r系相對(duì)于b系做旋轉(zhuǎn)運(yùn)動(dòng)的合成，則耦合轉(zhuǎn)動(dòng)下的圓錐變換四元數(shù)為：

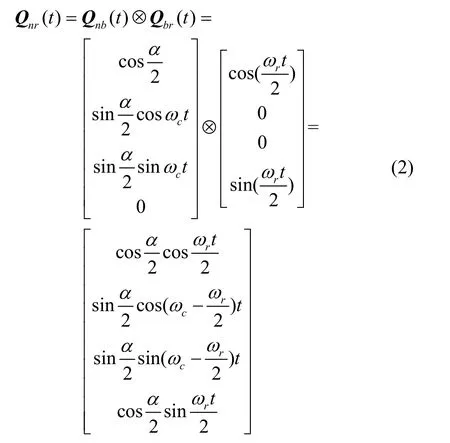
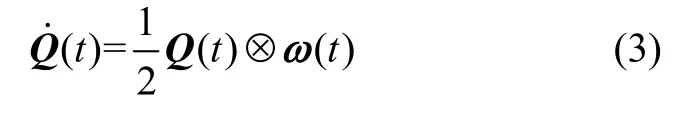
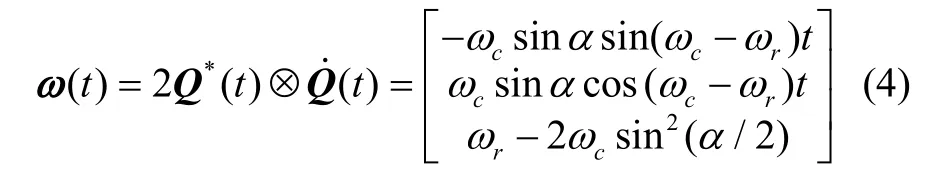
由式(2)和式(4)可得，當(dāng)轉(zhuǎn)位機(jī)構(gòu)存在旋轉(zhuǎn)角速度時(shí)，圓錐運(yùn)動(dòng)模型也將發(fā)生轉(zhuǎn)變。

1.2 單軸旋轉(zhuǎn)捷聯(lián)慣導(dǎo)系統(tǒng)中圓錐運(yùn)動(dòng)的等效旋轉(zhuǎn)矢量分析

由于剛體幾何轉(zhuǎn)動(dòng)的不可交換性的影響，使得利用IMU 的輸出在圓錐運(yùn)動(dòng)環(huán)境下進(jìn)行導(dǎo)航解算時(shí)存在誤差，體現(xiàn)在等效旋轉(zhuǎn)矢量的計(jì)算誤差。

以Q(tk)和Q(tk-1)分別表示在tk和tk-1時(shí)刻n系至r系的變換四元數(shù)，對(duì)應(yīng)的姿態(tài)變化四元數(shù)為q(h)，其中姿態(tài)更新周期h=tk-tk-1，根據(jù)四元數(shù)更新方程，有：

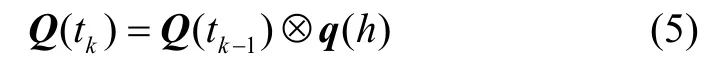
可得tk-1時(shí)刻至tk時(shí)刻對(duì)應(yīng)于r系的四元數(shù)q(h)：

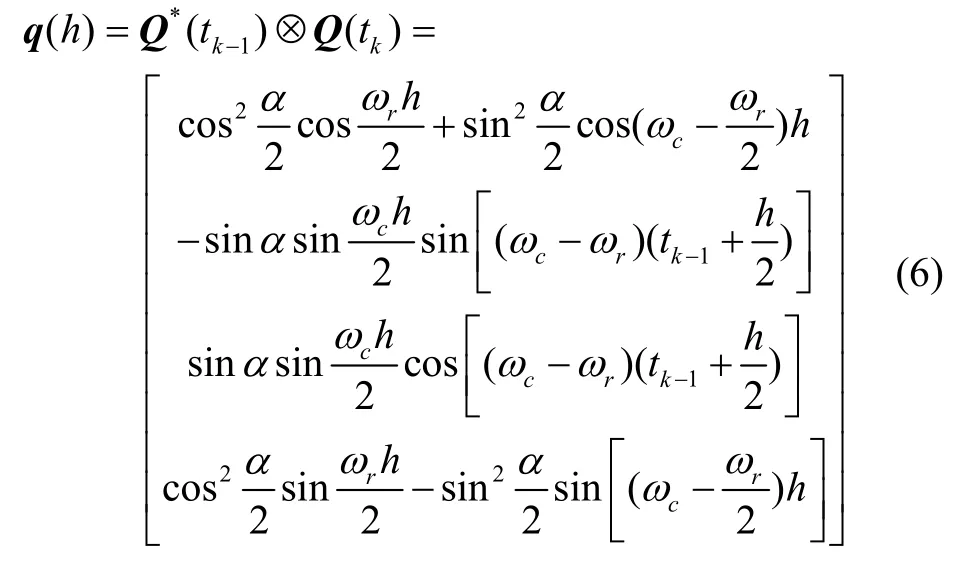
根據(jù)姿態(tài)變化四元數(shù)q(h)與等效旋轉(zhuǎn)矢量Φ(h)之間的對(duì)應(yīng)關(guān)系，有：

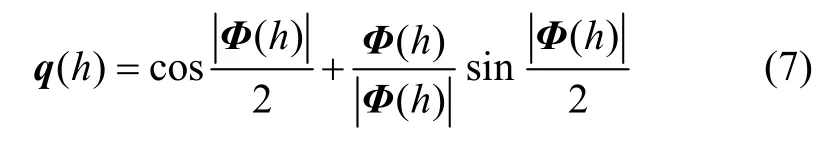
式中，|Φ(h)|是矢量Φ(h)的模，由于姿態(tài)更新周期一般都很短，可認(rèn)為Φ(h)為小量，簡化式(7)得：

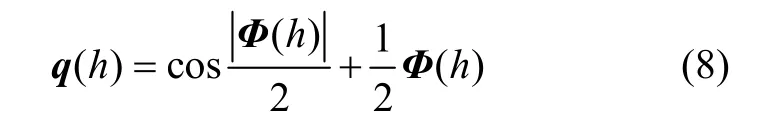
對(duì)比式(6)和式(8)的矢量部分可得：

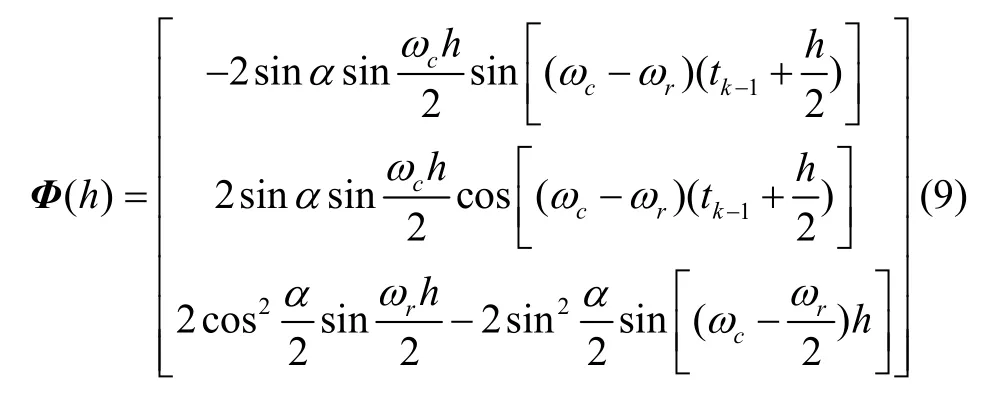
2 單軸RINS 中轉(zhuǎn)動(dòng)不可交換性誤差與圓錐誤差補(bǔ)償算法

在SINS 中，通常采用基于角速率/角增量的多子樣旋轉(zhuǎn)矢量算法補(bǔ)償不可交換性誤差。由于單軸RINS的圓錐運(yùn)動(dòng)特性發(fā)生改變，其補(bǔ)償形式也將會(huì)不同，因此需要研究姿態(tài)算法和轉(zhuǎn)位方案對(duì)圓錐誤差補(bǔ)償?shù)挠绊憽?/p>

2.1 轉(zhuǎn)動(dòng)不可交換性誤差分析

雖然光纖陀螺的輸出信號(hào)是角速率形式，但考慮到采樣量化電路，故實(shí)際使用的光纖陀螺大都是在高速率采樣的基礎(chǔ)上再作平均和降頻處理，其輸出信息更像是角增量。文獻(xiàn)[2]指出若將角速率形式信號(hào)轉(zhuǎn)換成角增量進(jìn)而構(gòu)造等效旋轉(zhuǎn)矢量，則在此轉(zhuǎn)換過程中會(huì)引入較大噪聲，為此設(shè)計(jì)了基于角速率輸入的廣義圓錐算法。基于角速率N子樣圓錐補(bǔ)償算法的基本原理是在每個(gè)姿態(tài)更新周期h內(nèi)獲得N+1 次陀螺采樣角速率ωi(i=0,1,2,…,N)，利用數(shù)值積分公式[2]由角速率估計(jì)角增量，并通過ωi之間的矢量叉乘對(duì)圓錐誤差補(bǔ)償項(xiàng)進(jìn)行逼近，等效旋轉(zhuǎn)矢量估計(jì)值?()hΦ為：

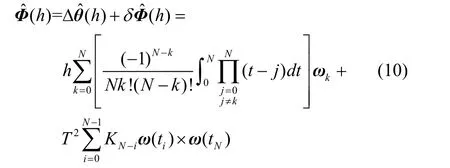
當(dāng)(ωc-ωr)h和ωch都是小量時(shí)，即有sin[(ωc-ωr)h]=(ωc-ωr)h，sin[ωch]=ωch，角增量估計(jì)值為：

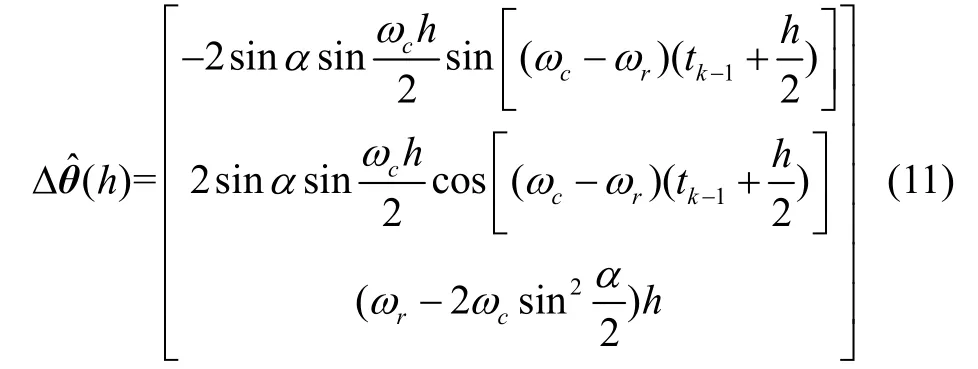
因此不可交換性誤差的理論值近似為：

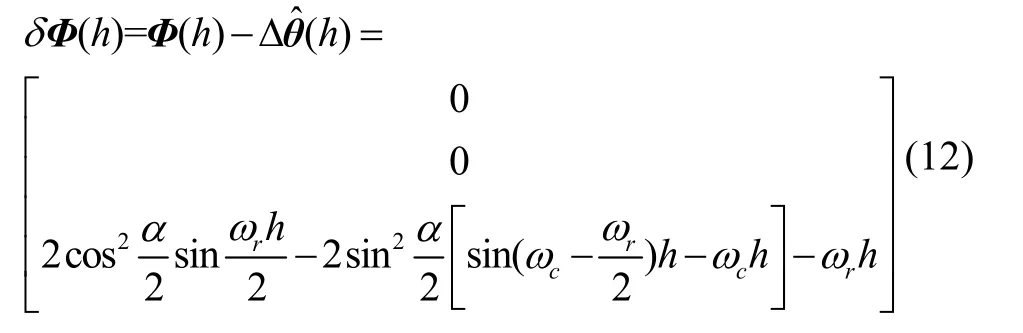
通過式(12)可以看出：

(1)基于角速率輸入下的單軸RINS 的不可交換性誤差在x軸與y軸分量為0，這與純SINS 的圓錐誤差一致。當(dāng)(ωc-ωr)h和ωch不都是小量時(shí)，單軸RINS的不可交換性誤差在x軸與y軸表現(xiàn)為周期量，其角頻率為ωc-ωr，幅度與子樣數(shù)有關(guān)。

(2)z軸常值誤差分量中引入了ωr及其與α的耦合項(xiàng)，相對(duì)SINS 發(fā)生了變化。

2.2 基于角速率的圓錐誤差補(bǔ)償算法分析

在對(duì)不可交換性誤差進(jìn)行補(bǔ)償時(shí)，將主要考慮其常量部分。根據(jù)式(12)有：

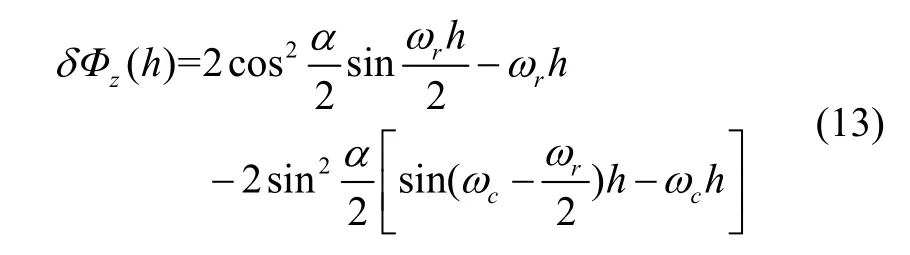
利用泰勒級(jí)數(shù)展開δΦz(mì)(h)中sin(ωc-ωr/2)h，可得：

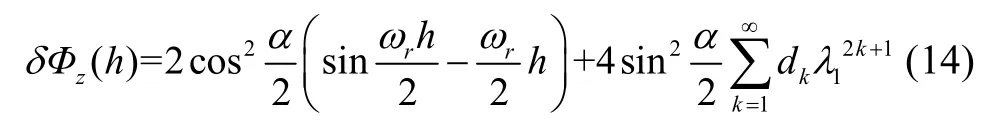
式中，dk=(-1)k+1N2k+1/[2(2k+1)!]，λ1=(ωc-ωr/2)T。

文獻(xiàn)[2]中基于角速率的圓錐誤差補(bǔ)償項(xiàng)通式為：

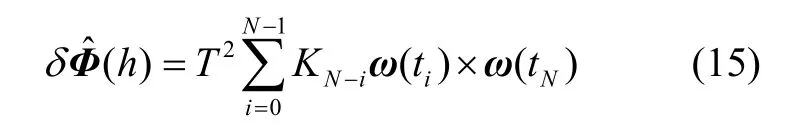
式中，KN-i為待優(yōu)化系數(shù)，將角速率公式(4)代入到ω(ti)×ω(tj)且i≠j，得：

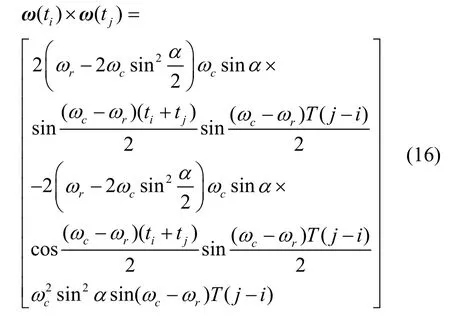
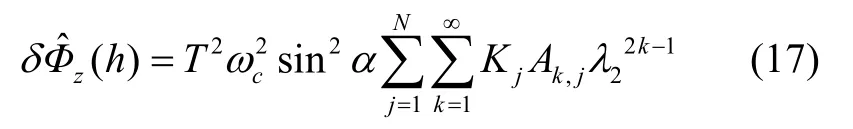
基于角速率的多子樣旋轉(zhuǎn)矢量算法常用式(17)對(duì)式(13)進(jìn)行逼近，待優(yōu)化系數(shù)為Kj(j=1,2…N)，對(duì)于純SINS，有λ1=λ2，因此可令式(17)和(13)相等，從而求解各子樣下的Kj。但在單軸RINS 中，λ1≠λ2，Kj取決于ωc和ωr，而在實(shí)際系統(tǒng)中ωc無法獲得，ωr也并非常值。根據(jù)實(shí)際工程中的應(yīng)用，令單軸RINS 中的Kj與SINS 的圓錐優(yōu)化系數(shù)一致，在此基礎(chǔ)上對(duì)圓錐誤差補(bǔ)償后的剩余誤差進(jìn)行分析。

比較式(17)和式(14)，可以看出在一個(gè)姿態(tài)更新周期內(nèi)單軸RINS 圓錐誤差補(bǔ)償?shù)氖Ｓ嗾`差包括4 部分：

(3)λ1和λ2的差異在補(bǔ)償時(shí)會(huì)產(chǎn)生誤差。

(4)多子樣算法在逼近圓錐補(bǔ)償項(xiàng)時(shí)存在剩余誤差，可近似為。

綜合以上分析，可得單軸旋轉(zhuǎn)捷聯(lián)慣導(dǎo)系統(tǒng)N子樣圓錐誤差補(bǔ)償算法的剩余誤差為：

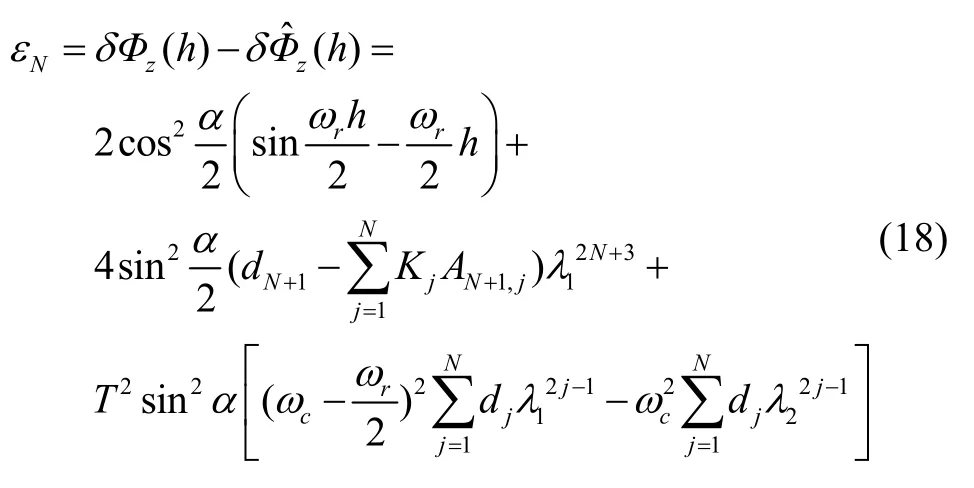
根據(jù)式(18)，可將剩余誤差分為3 類：

(1)εN的第一項(xiàng)誤差與算法的子樣數(shù)無關(guān)，由轉(zhuǎn)位機(jī)構(gòu)的旋轉(zhuǎn)角頻率所引起，不存在于SINS 中。

(2)εN的第二項(xiàng)誤差與圓錐運(yùn)動(dòng)角頻率、轉(zhuǎn)位機(jī)構(gòu)旋轉(zhuǎn)角頻率和算法子樣數(shù)相關(guān)。在角頻率不變下，增加算法的子樣數(shù)可減小該項(xiàng)誤差，SINS 中也存在類似誤差。

(3)εN的第三項(xiàng)誤差與圓錐運(yùn)動(dòng)角頻率、轉(zhuǎn)位機(jī)構(gòu)旋轉(zhuǎn)角頻率和算法子樣數(shù)相關(guān)，增加算法的子樣數(shù)可減小該項(xiàng)誤差，SINS 中不存在此類誤差。

在SINS 中，圓錐誤差的補(bǔ)償精度隨著子樣數(shù)的增加而提高。但在單軸RINS 中，由于εN中第一項(xiàng)剩余常值誤差的限制，使得多子樣算法的補(bǔ)償精度不再隨子樣數(shù)的增加而逐漸提高。

2.3 轉(zhuǎn)位方案對(duì)圓錐誤差補(bǔ)償?shù)挠绊?/h3>

綜合考慮轉(zhuǎn)位方案對(duì)陀螺水平常值漂移的調(diào)制效果和實(shí)際工程應(yīng)用成本，轉(zhuǎn)位機(jī)構(gòu)通常以多位置轉(zhuǎn)停的方式進(jìn)行正反方向旋轉(zhuǎn)。而在實(shí)際系統(tǒng)中，轉(zhuǎn)位機(jī)構(gòu)的啟停存在變速運(yùn)動(dòng)，即ωr是時(shí)間t的函數(shù)，若在轉(zhuǎn)位方案中頻繁引入變速運(yùn)動(dòng)，不僅會(huì)降低實(shí)際系統(tǒng)的誤差調(diào)制效果，還會(huì)影響圓錐運(yùn)動(dòng)模型及其誤差補(bǔ)償效果。

(1)多子樣算法補(bǔ)償不可交換性誤差后的剩余誤差是通過時(shí)間累積來影響單軸RINS。當(dāng)ωr在轉(zhuǎn)動(dòng)周期內(nèi)表現(xiàn)為正反向?qū)ΨQ時(shí)，εN中第1 項(xiàng)常值誤差在每個(gè)轉(zhuǎn)動(dòng)周期內(nèi)將相互抵消。

(2)在單軸RINS 的停留階段，其圓錐運(yùn)動(dòng)模型及剩余誤差εN與SINS 相同。

(3)轉(zhuǎn)位機(jī)構(gòu)的變速運(yùn)動(dòng)，不僅直接影響了IMU位置和速率的對(duì)稱性，還間接影響了不可交換性誤差的補(bǔ)償效果。

3 仿真實(shí)驗(yàn)與分析

針對(duì)以上對(duì)單軸RINS 在圓錐運(yùn)動(dòng)下不可交換性誤差補(bǔ)償?shù)睦碚撏茖?dǎo)與分析，將通過仿真比較轉(zhuǎn)位方案對(duì)姿態(tài)誤差的影響以及基于角速率的多子樣旋轉(zhuǎn)矢量法對(duì)圓錐誤差補(bǔ)償?shù)男Ч?/p>

3.1 單軸旋轉(zhuǎn)捷聯(lián)慣導(dǎo)系統(tǒng)中轉(zhuǎn)位方案對(duì)圓錐誤差影響仿真

仿真總體條件設(shè)置如下：半錐角α為1 °，圓錐運(yùn)動(dòng)頻率為1 Hz，陀螺采樣周期T=0.005 s，仿真時(shí)間20 min，假設(shè)b系相對(duì)n系做典型圓錐運(yùn)動(dòng)，姿態(tài)更新算法采用基于角速率的二子樣旋轉(zhuǎn)矢量算法。

當(dāng)旋轉(zhuǎn)角速度ωr為0 時(shí)，其姿態(tài)誤差如圖1所示；當(dāng)轉(zhuǎn)位機(jī)構(gòu)以ωr=16 °/s 單方向持續(xù)旋轉(zhuǎn)時(shí)，其姿態(tài)誤差如圖2所示；當(dāng)轉(zhuǎn)位機(jī)構(gòu)以旋轉(zhuǎn)角速度ωr=16 °/s，旋轉(zhuǎn)角加速度ar=8 °/s2單位置正反轉(zhuǎn)停時(shí)，其姿態(tài)誤差如圖3所示，停轉(zhuǎn)時(shí)間為2.5 min；當(dāng)轉(zhuǎn)位機(jī)構(gòu)以ωr=16 °/s，ar=8 °/s2四位置轉(zhuǎn)停，四位置轉(zhuǎn)位停的順序?yàn)椋? °→180 °→270 °→90 °→0 °，其姿態(tài)誤差如圖4所示。其中ΔH、ΔP、ΔR分別表示載體的航向角、俯仰角和橫滾角誤差。

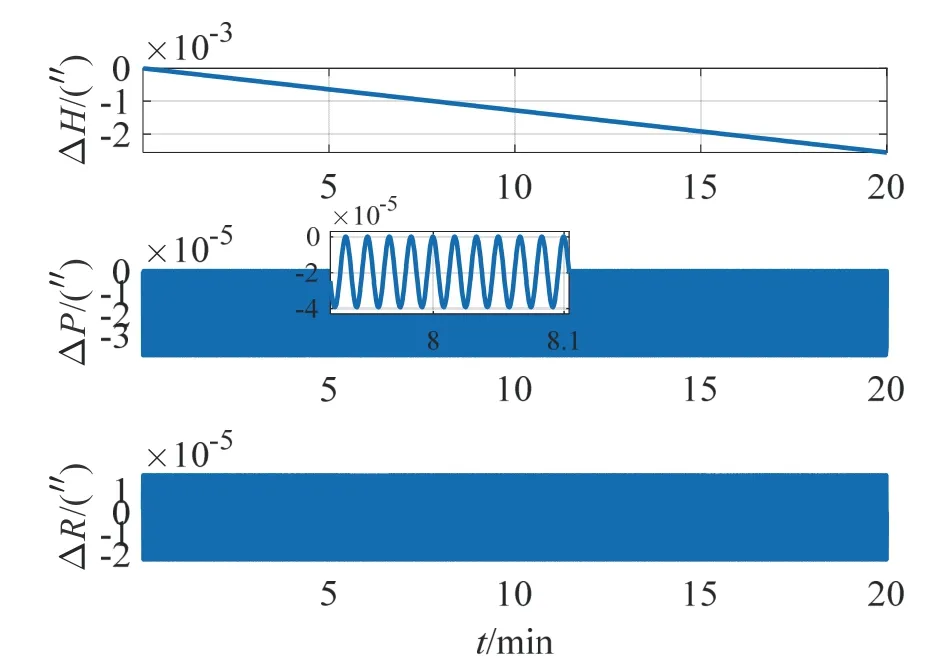
圖1 零速旋轉(zhuǎn)下姿態(tài)誤差Fig.1 Attitude error under zero speed rotation

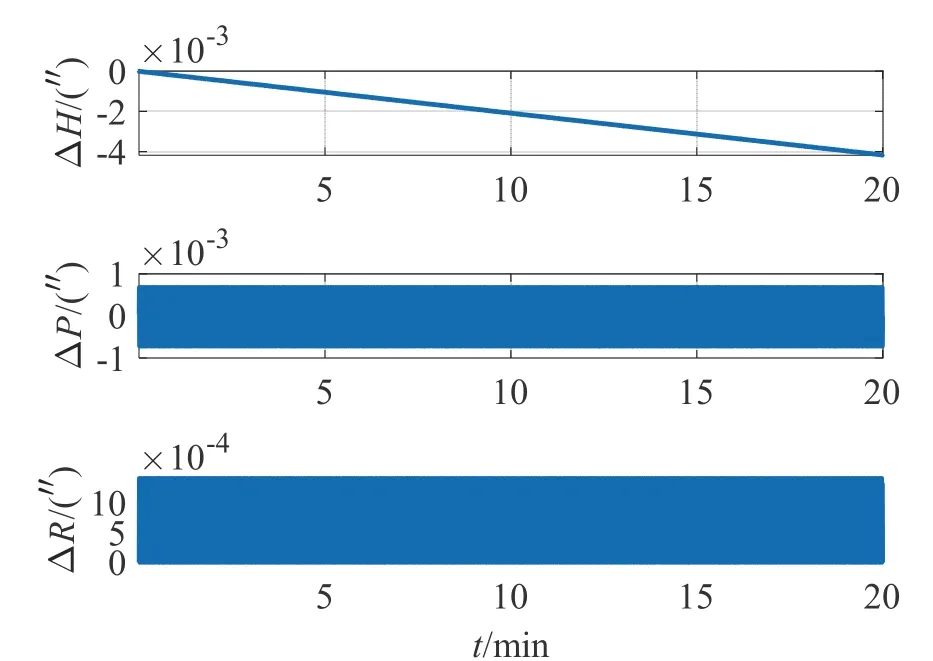
圖2 單向勻速旋轉(zhuǎn)下姿態(tài)誤差Fig.2 Attitude error under unidirectional rotation

由圖1 可以看出，轉(zhuǎn)位機(jī)構(gòu)停轉(zhuǎn)條件下的姿態(tài)誤差變化與SINS 一致；相對(duì)零速轉(zhuǎn)動(dòng)，圖2 中當(dāng)轉(zhuǎn)位機(jī)構(gòu)存在轉(zhuǎn)速時(shí)，航向角誤差增大0.6 倍，水平姿態(tài)角誤差波動(dòng)幅度增大1～2 個(gè)數(shù)量級(jí)。對(duì)比圖2、圖3和圖4 可知，通過轉(zhuǎn)位機(jī)構(gòu)的正反轉(zhuǎn)可降低航向角誤差和水平姿態(tài)角誤差，但由于在啟停過程中引入了變速運(yùn)動(dòng)，導(dǎo)致水平姿態(tài)角誤差在短時(shí)間內(nèi)有劇烈的周期振動(dòng)，比停轉(zhuǎn)階段的誤差幅度大2～3 個(gè)數(shù)量級(jí)。單軸RINS 在圓錐運(yùn)動(dòng)下的水平姿態(tài)角誤差仍是呈現(xiàn)出周期性變化，故主要考慮航向角誤差，四種轉(zhuǎn)位方案下的航向角誤差仍隨時(shí)間發(fā)散，由表1 知四位置轉(zhuǎn)停方案下的航向角誤差最小，但其啟停階段的航向角誤差要比停轉(zhuǎn)階段的誤差大3 個(gè)數(shù)量級(jí)，持續(xù)時(shí)間取決于啟停的時(shí)間差，在本節(jié)仿真中轉(zhuǎn)過90 °和180 °所需的時(shí)間分別為7.625 s 和13.25 s。

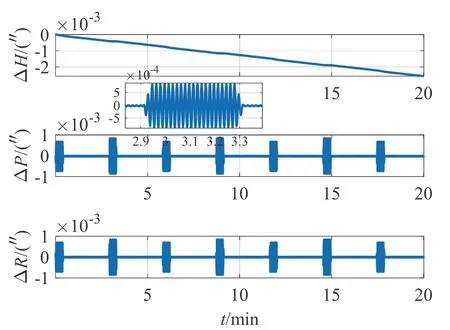
圖3 正反轉(zhuǎn)停下姿態(tài)誤差Fig.3 Attitude error under reversible switch-stop

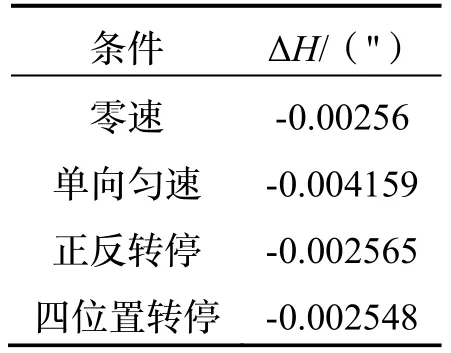
表1 仿真20 min 后航向角誤差Tab.1 Heading error after 20 minutes of simulation

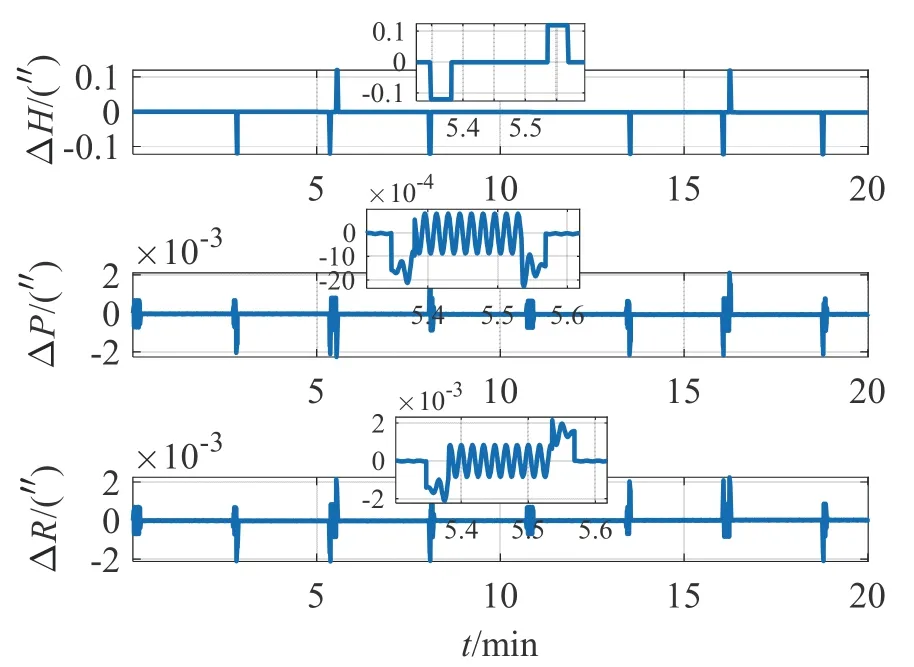
圖4 四位置轉(zhuǎn)停下姿態(tài)誤差Fig.4 Attitude error under four-position switch-stop

3.2 四位置轉(zhuǎn)停下基于角速率的多子樣旋轉(zhuǎn)矢量算法對(duì)圓錐誤差影響仿真

仿真總體條件設(shè)置如下：半錐角α為1 °，圓錐運(yùn)動(dòng)頻率為1 Hz，旋轉(zhuǎn)角速度ωr=16 °/s，旋轉(zhuǎn)角加速度ar=8 °/s2，陀螺采樣周期T=0.005 s，仿真時(shí)間20 min，假設(shè)b系相對(duì)n系做典型圓錐運(yùn)動(dòng)。四位置轉(zhuǎn)停的順序?yàn)椋? °→180 °→270 °→90 °→0 °，轉(zhuǎn)位機(jī)構(gòu)的旋轉(zhuǎn)角度和角速度如圖5所示，包括勻加速、勻速、勻減速和停轉(zhuǎn)四個(gè)階段，停轉(zhuǎn)時(shí)間為2.5 min。分別采用基于角速度的三子樣、四子樣和五子樣等效旋轉(zhuǎn)矢量算法對(duì)單軸旋轉(zhuǎn)捷聯(lián)慣導(dǎo)的圓錐誤差進(jìn)行補(bǔ)償后，其姿態(tài)誤差分別如圖6、圖7 和圖8所示。

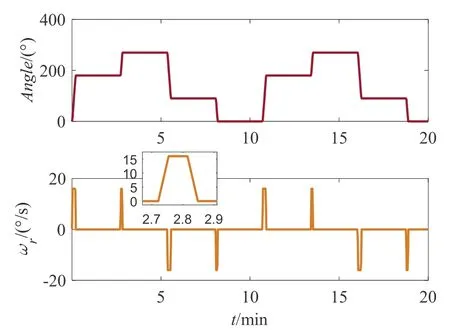
圖5 轉(zhuǎn)位機(jī)構(gòu)的角度和角速度變化Fig.5 Change of angle and angular velocity of indexing mechanism

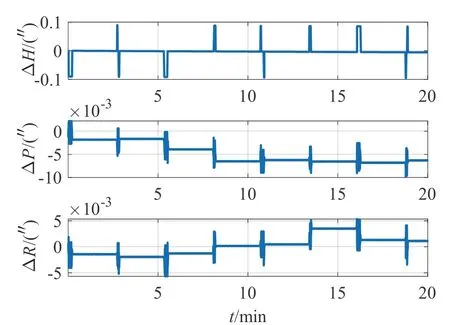
圖6 三子樣算法姿態(tài)誤差Fig.6 Attitude error of triple-sample algorithm

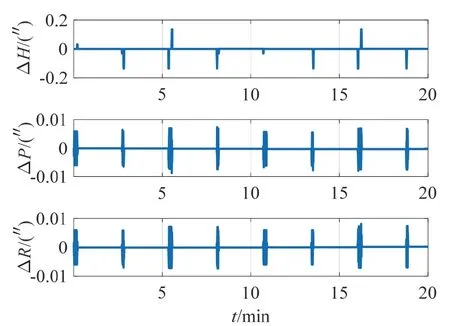
圖7 四子樣算法姿態(tài)誤差Fig.7 Attitude error of four-sample algorithm

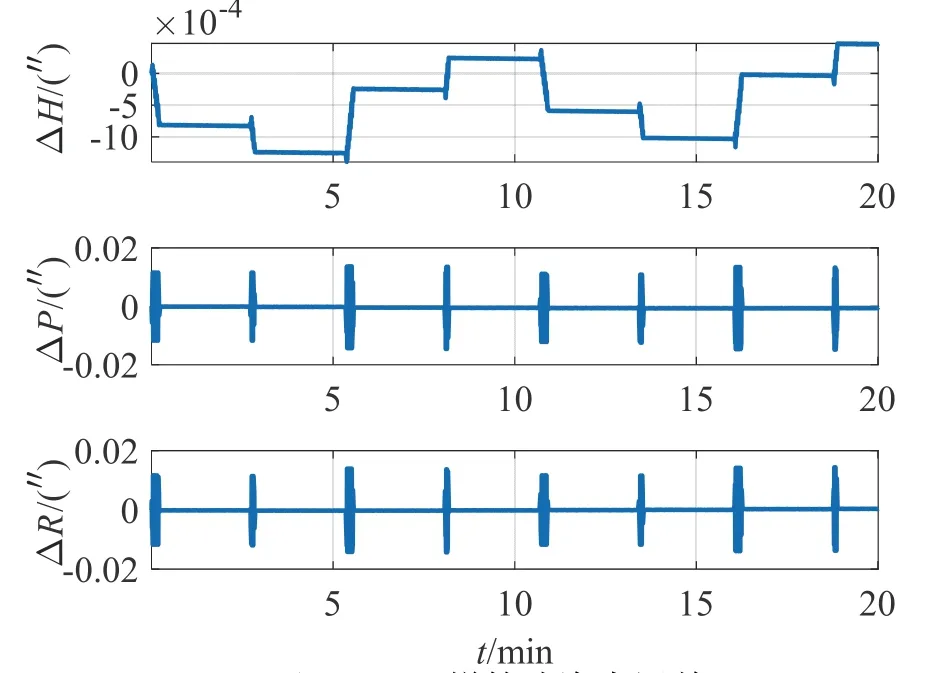
圖8 五子樣算法姿態(tài)誤差Fig.8 Attitude error of five-sample algorithm

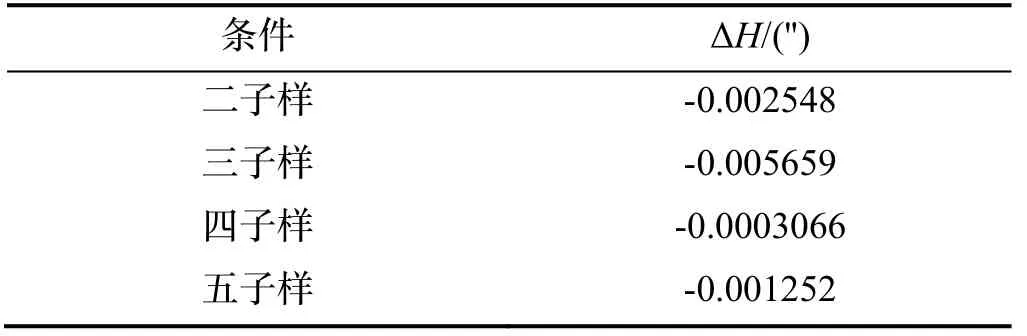
表2 停轉(zhuǎn)階段最大航向角誤差Tab.2 Maximum heading error during stop phase

對(duì)比圖4、圖6、圖7 和圖8，可以看出，在陀螺采樣頻率固定的情況下，由于不同子樣算法的姿態(tài)更新周期不同，導(dǎo)致圓錐誤差補(bǔ)償效果未因子樣數(shù)的增加而提高。其中三子樣補(bǔ)償后的水平姿態(tài)誤差最大且呈發(fā)散趨勢(shì)，五子樣補(bǔ)償后的航向角誤差呈階梯式變化。由表2 知，采用四子樣補(bǔ)償算法下的航向角誤差最小，且水平姿態(tài)角誤差呈現(xiàn)周期變化，補(bǔ)償效果相對(duì)較好。結(jié)合工程實(shí)際中IMU 輸出頻率固定和計(jì)算實(shí)時(shí)性要求，可采用基于角速率的四子樣補(bǔ)償算法。

4 總結(jié)與展望

本文通過理論分析和仿真，得出以下結(jié)論：

(1)單軸RINS 的圓錐誤差及其補(bǔ)償后的剩余誤差大于SINS 中的誤差，通過增加基于角速率/角增量的旋轉(zhuǎn)矢量算法的子樣數(shù)不能無限提高圓錐誤差補(bǔ)償精度；轉(zhuǎn)位方案會(huì)影響圓錐誤差的補(bǔ)償精度，四位置轉(zhuǎn)停方式的誤差補(bǔ)償效果最好。

(2)在四位置轉(zhuǎn)停方案中，啟停階段的航向角誤差會(huì)急劇增大，其持續(xù)時(shí)間在10 s 左右，雖然對(duì)RINS的導(dǎo)航定位解算影響不大，但對(duì)以RINS 為主的組合導(dǎo)航系統(tǒng)來說可能會(huì)造成濾波校正后的結(jié)果變差，故應(yīng)盡量降低RINS 啟停頻率或延長停轉(zhuǎn)時(shí)間。

(3)RINS 中圓錐誤差隨載體搖擺幅度和搖擺頻率的增大而增大；現(xiàn)有圓錐算法大都在假設(shè)陀螺輸出無誤差的前提下設(shè)計(jì)姿態(tài)誤差補(bǔ)償系數(shù)且其實(shí)際精度尚未得到驗(yàn)證，然而陀螺輸出信號(hào)中包含了隨機(jī)誤差、安裝誤差、標(biāo)度因素誤差和量化等誤差，導(dǎo)致實(shí)際信號(hào)中難以保留理論運(yùn)動(dòng)假設(shè)下的全部特性，進(jìn)而造成圓錐誤差補(bǔ)償效果不理想，因此如何提高高動(dòng)態(tài)條件下圓錐誤差的實(shí)際補(bǔ)償精度是下一步的研究方向。