慣組小系統動力學建模與非線性特性分析

商 霖，張海瑞，趙曉寧

（中國運載火箭技術研究院，北京 100076）

慣組小系統是由慣組、基座和減振器等組成。飛行器飛行過程中，慣組小系統將經歷長時大振動、短時強沖擊和持續高過載及高溫等惡劣環境，嚴重影響了其測量精度和使用壽命。慣組陀螺信號受外界角振動環境的影響會迭加基座和減振器的角振動分量，導致陀螺測量出現誤差，直接影響到飛行穩定性。慣組加表信號受外界線振動環境的影響會疊加基座和減振器的高頻振動分量、引入虛假的運動，導致加表測量出現誤差，進而影響到導航精度。工程上，通過將基座設計為剛性平臺以消除其負面影響，由此慣組小系統線/角傳遞特性主要取決于減振器環節的合理布局[1,2]和優化設計[3-5]。

減振器作為一種彈性元件，主要用于降低慣組承受的振動和沖擊等環境。當前在減振器研究中，往往采用線性化模型進行相關設計和分析[1-6]。實際的減振器是一個非線性的漸軟系統，忽略非線性效應的線性化模型不能體現系統的非線性軟化特征，也就無法準確地進行非線性特性的研究，甚至導致錯誤的結果，因此有必要開展慣組小系統非線性動力學建模和非線性特性分析工作。

非線性動力學的研究最早可以追溯到Rosenberg[7]的工作，他提出了非線性模態的概念，奠定了相關理論。Shaw[8]和Nayfeh[9]等相繼拓展了非線性模態的定義，推動了該領域的研究發展。Sun[10]等采用復化平均法得到了由簡諧外力和非線性能量阱組成的非線性振動系統在穩態響應下的解析解，并通過數值模擬對解析模型進行驗證，得到了系統動態失穩的初步認識。Mezghani[11]等提出了一種非線性參數識別方法用于識別非線性振動系統的剛度和阻尼系數。No?l[12]則綜述了從2006年來近十年間非線性系統參數辨識領域出現的關鍵技術，通過討論實驗模型在工程結構設計中的核心作用，為這一領域的發展提供了一個更為廣闊的視角。王丹[13]等利用試驗結果辨識得到非線性恢復力模型，并將其應用于橡膠減振器的動力學分析。杭超等[14]利用振動臺掃頻測得了兩類橡膠減振器的動剛度和阻尼比。唐安特等[15]采用Mooney-Rivlin 模型和Maxwell 模型疊加組成的非線性粘彈性本構模型計算了橡膠減振器的高頻動態特性。

為了研究高量級振動環境對慣組小系統非線性特性的影響，本文將減振器簡化成具有立方剛度的三自由度非線性系統，建立了基礎激勵下的動力學模型，方程中的物理參數取自于真實產品的慣組小系統。隨后，采用單自由度激勵方式進行慣組小系統傳遞特性試驗，利用仿真模擬結果驗證本文非線性動力學模型的正確性。最后，采用龍格-庫塔法對不同激勵幅值下減振器的非線性動剛度特性進行了數值模擬，采用虛弧長延拓方法給出了不同激勵幅值下慣組小系統的非線性頻響函數和傳遞特性及慣組減振器可以適應的飛行振動邊界。

1 慣組小系統動力學模型

1.1 模型簡化

慣組小系統基本組成如圖1所示。其中，將慣組視為剛體；基座處理為剛性基礎面；四個減振器（編號分別為1、2、3、4）采用平面四點布局的方式均布在慣組的四個邊角，構成整個慣組小系統的減振系統。圖1 中，直角坐標系oxyz的坐標原點o位于慣組質心處，慣組質量為4m；坐標軸xyz為過慣組質心的主慣性軸以消除剛體慣性積，其相應的轉動慣量分別為4Ix、4Iy和4Iz；四個減振器均簡化為無質量的單向彈簧-阻尼元件，其安裝位置相對xy和xz面對稱，若選用同一規格的減振器，即可實現慣組質心、形心和減振器彈性中心的“三心重合”設計，由此保證了對稱面內線、角運動的線性解耦，從而獲得理想的減振系統。

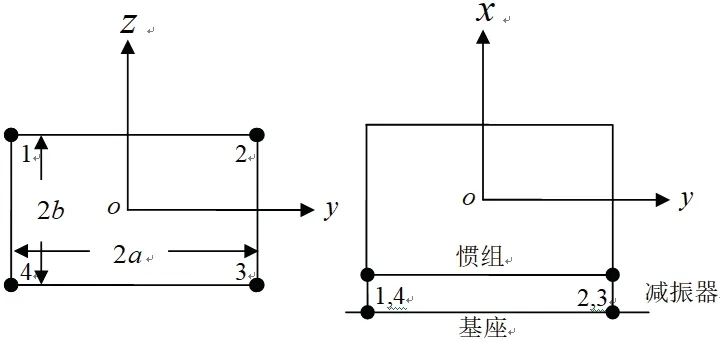
圖1 慣組小系統模型Fig.1 The combined model of inertial navigation system

1.2 運動方程

根據飛行姿態需求，僅考慮慣組x垂向、Rz或α俯仰和Ry或β偏航等三個自由度/方向的剛體運動。由此，可令基座的基礎激勵輸入為xi、αi和βi，慣組的剛體響應輸出為x、α和β。當基座相對慣組運動時，減振器將阻止這樣的運動，按多體動力學方法，則可得到慣組小系統的運動方程：

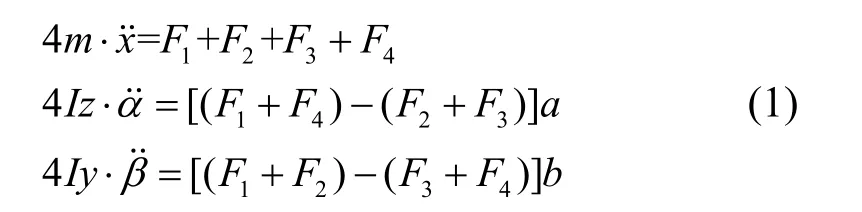
考慮小平移和小轉動情況，此時轉動是可交換的（即最終位置與轉動分量的順序無關），由此基座和慣組在四個減振器位置的位移就是其平動線位移加上轉動角位移的切向分量，可分別表示為：

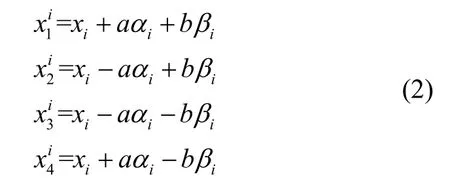
和

進而，由式(2)和式(3)可以得到四個減振器的變形（且規定壓為正），即

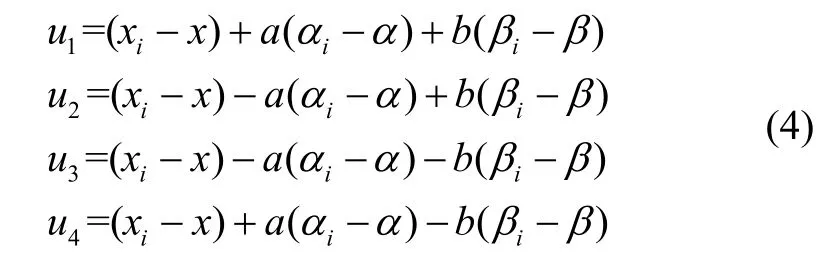
1.3 非線性動力學方程

振動過程中，慣組小系統的減振系統通常選用同一規格的減振器，且嚴格要求其剛度和阻尼特性保持一致。

因此，這里令ci=c、ki1=k1和ki2=k2，其中i=1,2,3,4。將式(4)代入式(1)可得到如下運動方程：

若用xr=x-xi、αr=α-αi和βr=β-βi表示慣組相對于基座的運動，則式(5)可表示為

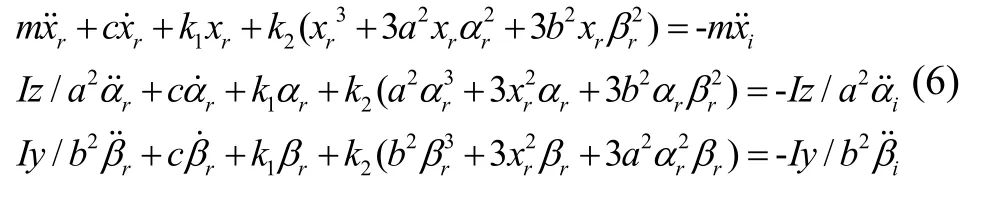
由式(6)所示的含立方項非線性減振器的動力學方程可知，慣組小系統的質量、阻尼和線性剛度項是解耦的，此時若非線性剛度系數k2=0則系統退化為三個單自由度系統，可以獨立求解，即實現了線、角振動的分離。若k2≠0則非線性剛度項在線、角位移上引入了耦合關系，k2>0表征為漸硬特性系統，k2<0表征為漸軟特性系統。

2 慣組小系統傳遞特性試驗

2.1 試驗原理

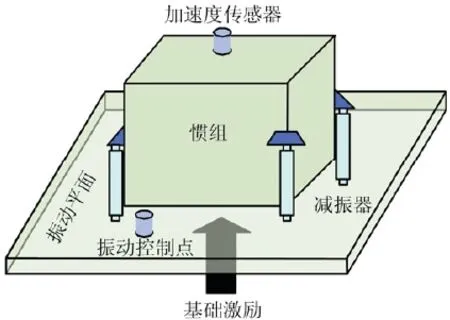
圖2 慣組小系統基礎激勵原理性試驗系統Fig.2 Basic excitation principle test system of inertial navigation system

針對某型慣組小系統，工程研制初期搭建了純線/角振動的原理性試驗系統，采用單自由度激勵的方式研究其傳遞特性。如圖2所示[16]，慣組通過橡膠減振器連接在振動平臺上，電動振動臺對振動平臺施加正弦掃頻激勵。振動控制點在振動平臺上，通過控制加速度傳感器的安裝位置和響應量級實現線/角振動的常幅激勵。慣組上安裝加速度傳感器測量減振后信號，或直接采集慣組陀螺或加表的數據。

2.2 試驗結果

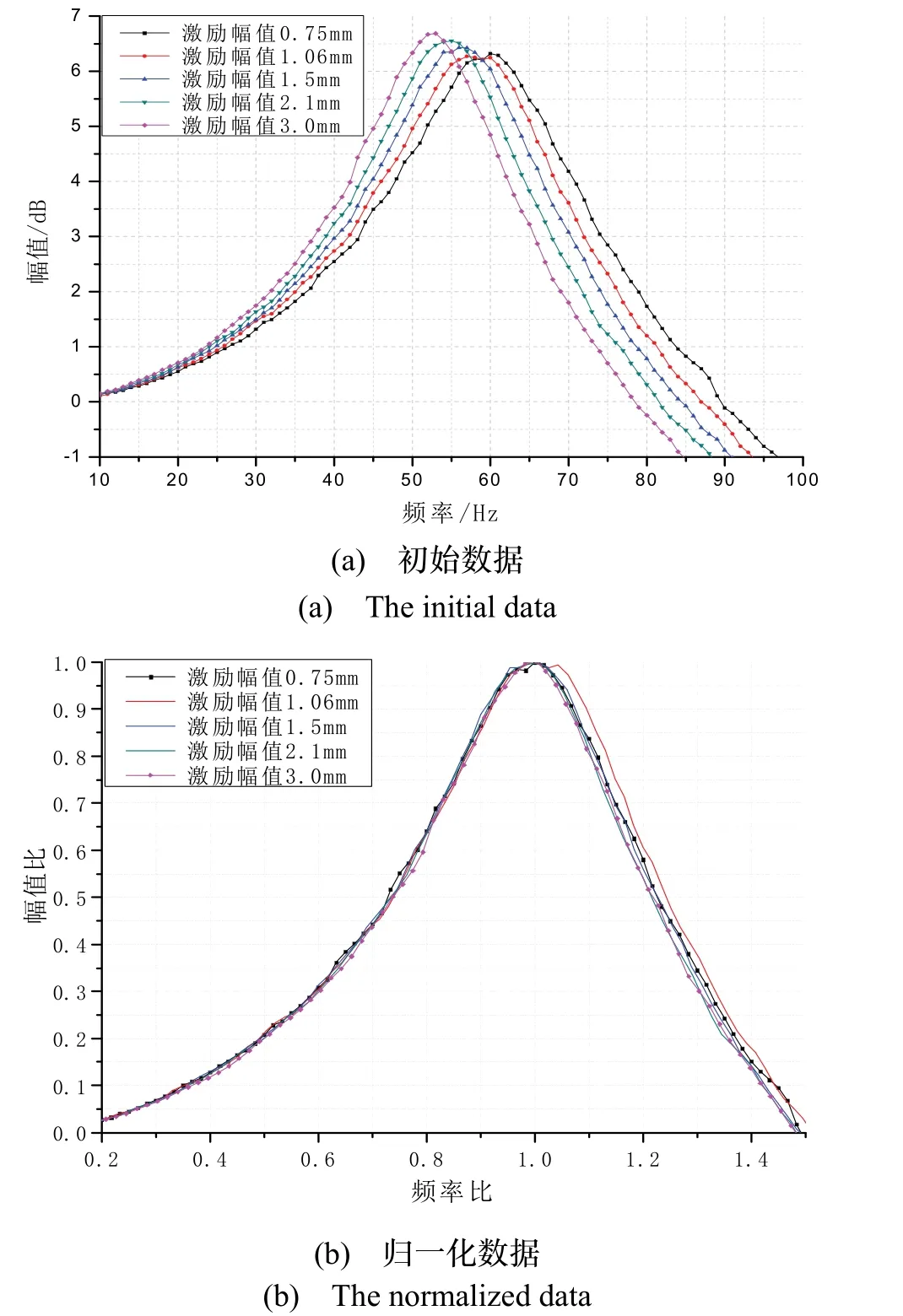
圖3 慣組小系統傳遞特性Fig.3 Transfer characteristics of inertial navigation system

圖3 給出了利用正弦掃頻激勵法得到的慣組小系統線振動傳遞特性。角振動傳遞特性試驗結果類同線振動。考慮篇幅所限，相關圖示略去。圖3(a)中，隨著激勵幅值的逐級增大，系統峰值頻率逐漸減小，這表明橡膠減振器呈現出含有漸軟剛度的非線性特征。通過對圖3(a)中不同激勵幅值傳遞曲線進行歸一化處理，即頻率相對峰值頻率歸一化、幅值相對峰值幅值歸一化，可以得到圖3(b)。

圖3(b)中，不同激勵幅值下慣組小系統傳遞特性曲線完全重合，由此表明：1）圖3(a)中系統峰值頻率的變化，是由于激勵幅值的不同導致減振器動剛度不同；2）不同激勵幅值下，減振器的阻尼比系數基本不變。

2.3 數值模擬

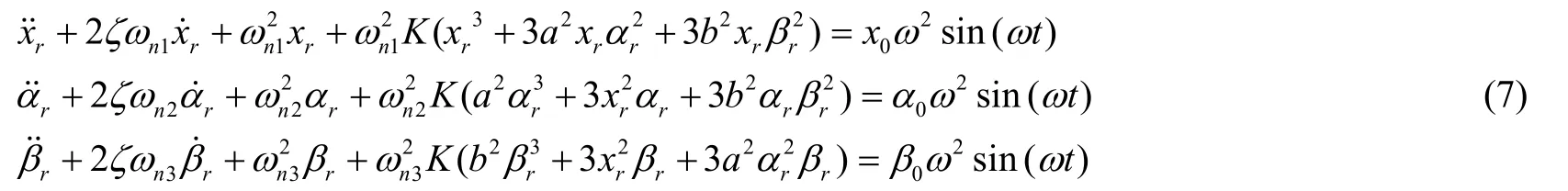
式中，ξ是阻尼比系數，是垂向線頻率，是俯仰角頻率，是偏航角頻率，是剛度系數比，x0是線激勵幅值，α0是俯仰角激勵幅值，β0是偏航角激勵幅值，ω是線/角激勵頻率。

若模擬純線運動的正弦激勵，則可令x0≠0，而α0=0和β0=0。若模擬純俯仰的正弦激勵，則可令α0≠0，而x0=0和β0=0。同理，也可模擬純偏航的正弦激勵。由此，式(7)中垂向線運動、俯仰和偏航角運動的獨立表示可以統一采用如下單自由度非線性運動微分方程

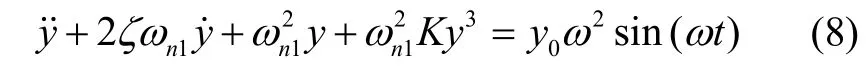
式中，y可分別用于代替垂向線位移xr、俯仰角位移αr和偏航角位移βr。為節省篇幅，下文僅對慣組小系統純線振動傳遞特性進行分析。純角振動傳遞特性的分析可據此進行。

本文研究中，橡膠減振器的基本參數：線性剛度系數k1=2.15 ×104N/m，非線性剛度系數k2=-3.2 ×107N/m3，阻尼系數c=18.9 N ·s/m ；慣組質量特性參數m=0.16kg 。

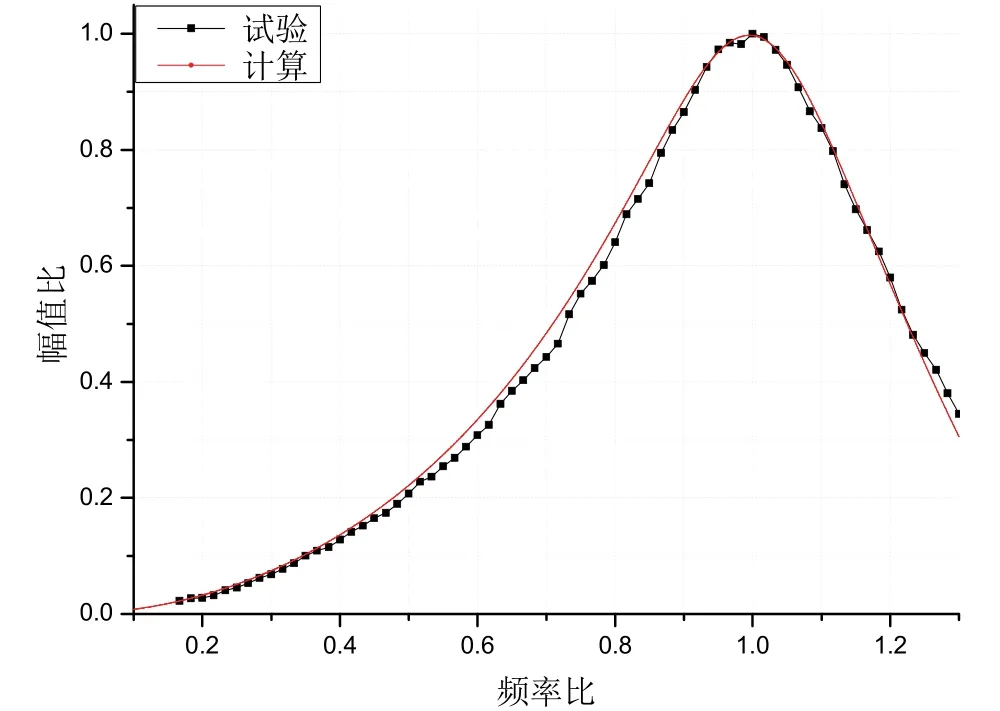
圖4 慣組小系統試驗結果與數值計算結果的比對Fig.4 Comparison of test results of inertial navigation system with numerical results

圖4 給出了采用龍格-庫塔數值方法計算式(8)所得數值結果與圖3(b)正弦掃頻試驗結果的對比，二者吻合良好。利用數據統計分析可得，計算結果與試驗結果均值偏差僅為1.73%，矢量偏差約1.95%，二者相關度達到了99.9%，吻合度為96.5%。由此表明，慣組小系統非線性動力學模型和模型參數可以真實地表征系統傳遞特性。

3 非線性特性分析

上文試驗結果表明橡膠減振器具有“軟彈簧”特性，但缺乏直觀的動剛度曲線的驗證，也并未真正地表現出非線性動態特性。試驗過程中橡膠減振器運動范圍在線性、小變形范圍內，其力學特性仍是線性的。式(8)中表征橡膠減振器非線性特性的主要參數是剛度系數比K，而誘發這一非線性特性的最直接的因素則是激勵幅值y0。下文研究大激勵幅值下，橡膠減振器的非線性動剛度特性和慣組小系統的非線性頻響函數及傳遞特性。

3.1 系統動剛度與減振器動剛度

文獻[13-15][17]從試驗分析、理論推導和數值計算等多個方面研究了非線性系統的動剛度，這些研究工作出發點各不相同，對動剛度的理解和定義也不盡相同。

本文認為慣組小系統包含著兩個層級的動剛度，即系統層級的動剛度和橡膠減振器層級的動剛度。系統動剛度包含了慣組質量、減振器剛度和阻尼等，其可表示為

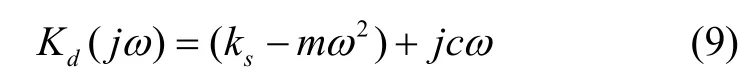
式中，ks為減振器靜剛度。橡膠減振器動剛度則由彈性回復力-位移曲線表征，其可表示為

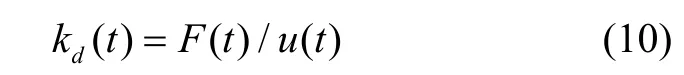
式中，F(t)是減振器的彈性回復力，u(t)是減振器的位移。

采用龍格-庫塔積分算法得到式(8)的數值解，并對系統動剛度和減振器動剛度進行分析。計算中，激勵幅值y0分別取為0.75 mm、1.5 mm、3 mm、4.5 mm、6 mm 和10 mm 等6 個量級，激勵頻率ω取值范圍為0.1 Hz～120 Hz，掃頻速率2 Oct/min。

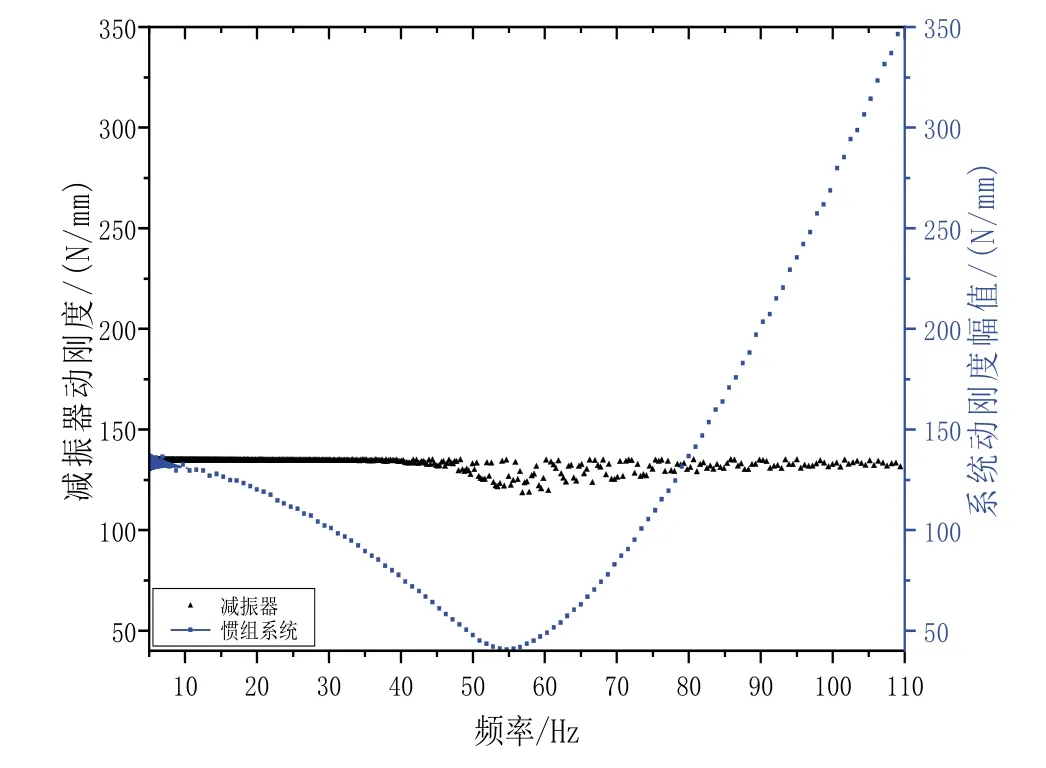
圖5 系統動剛度和減振器動剛度的比對Fig.5 Comparison of dynamic stiffness of inertial navigation system and rubber damper

考慮篇幅所限，文中僅從眾多計算結果中選出激勵幅值3 mm 時系統動剛度幅值與減振器動剛度的比對，如圖5所示。從圖5 中可看出，相同振幅下系統動剛度隨激勵頻率的變化比較明顯，在共振頻率點達到最小，表明共振頻率附近系統特性主要由阻尼項控制；在低頻段動剛度基本等于靜剛度，表明共振頻率以下系統特性主要由占主導地位的剛度項來描述；在高頻段動剛度隨激勵頻率的增加持續變大，表明共振頻率以上系統特性主要由占主導地位的質量項來描述。同一振幅下減振器動剛度幾乎不受激勵頻率的影響，在低頻段其動剛度接近靜剛度，在系統共振頻率附近波動明顯、相對量較小。已有計算結果還表明，激勵幅值越大、波動越明顯，但波動規律性不強。

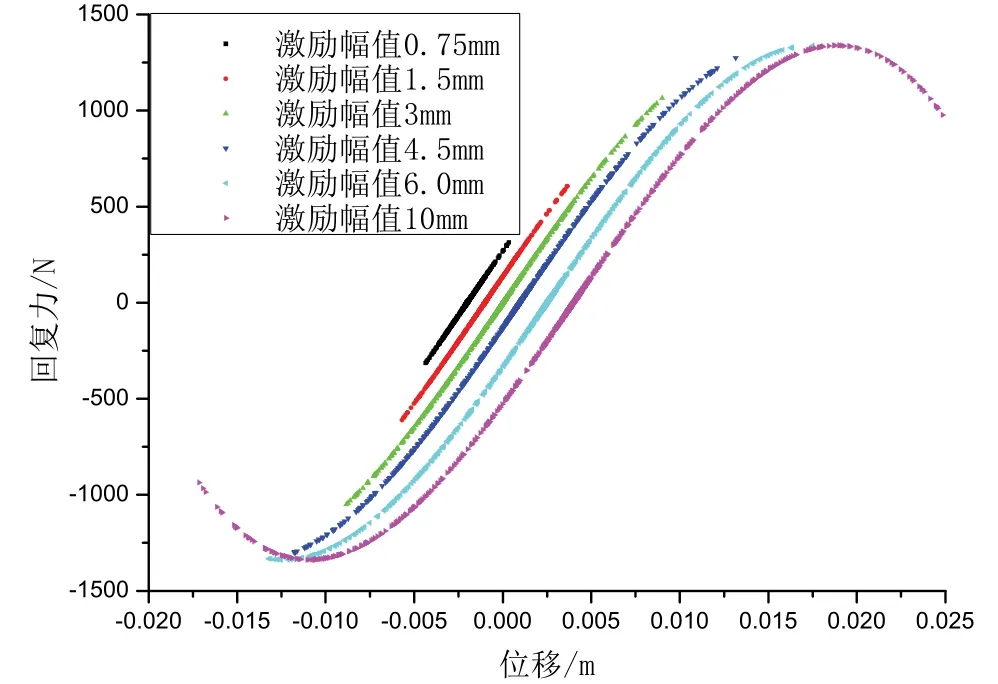
圖6 不同激勵幅值下減振器回復力-位移曲線Fig.6 Restoring force-displacement curve of rubber damper under different excitation amplitudes

圖6 給出了不同激勵幅值下減振器回復力-位移曲線的比對。為便于觀察，圖6 曲線在位移軸方向作了人為的整體移動，即人為改變不同激勵幅值下位移零點，簡單來說，0.75 mm 激勵時位移零點調整為0.001 m，1.5 mm 激勵時，位移零點調整為0.002 mm，以此類推。若不作移動，6 個激勵幅值下的回復力-位移曲線將完全重合。由圖6 可見，激勵幅值小于3.0 mm時，載荷-位移曲線近似呈一條直線，表明減振器處于彈性范圍內；激勵幅值大于3.0 mm 時，隨著激勵幅值的增加，減振器表現出漸進軟化的非線性特性。

3.2 頻響函數與傳遞特性

實際飛行過程中，橡膠減振器不可能僅停留在小變形工況下，大變形工況也是不可避免的。為了探究橡膠減振器在更為嚴酷飛行環境下的使用能力，了解其特性的穩定性，是否會出現分岔的現象[10,18,19]。本節重點研究不同激勵幅值下橡膠減振器的非線性傳遞特性和頻響函數。

針對橡膠減振器這類具有較強非線性特性的系統，傳統打靶法在求解其周期解時往往會遇到在分岔點處雅克比矩陣奇異的情況，此時就需要用到延拓算法。本文利用虛弧長延拓方法編制計算程序對式(8)進行求解，獲得慣組小系統的傳遞特性和頻響函數，分別見圖7 和圖8。

計算中，激勵幅值y0取值同3.1 節，激勵頻率ω取值范圍為5 Hz～300 Hz。為了區別于傳統意義上的掃頻試驗，這種沿頻率范圍延拓的方法，可稱為數值上的“掃頻法”。

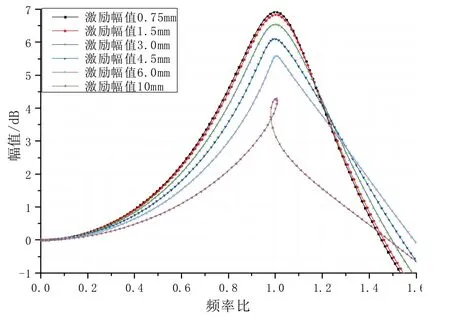
圖7 慣組小系統非線性傳遞特性Fig.7 Nonlinear transfer characteristics of inertial navigation system

圖7 計算結果表明，激勵幅值3.0 mm 時減振器開始表現出輕微的非線性特性，在非線性范圍內激勵幅值越大，系統損耗越大、峰值變尖，半功率帶寬變小。激勵幅值10 mm 時，傳遞曲線發生了扭曲、變形，形成了一個回路轉折點，表明系統特性不太穩定。

圖8 中，激勵幅值3.0 mm 時，頻響曲線的共振峰出現了明顯的偏左彎曲，在非線性范圍內激勵幅值越大，系統的軟化特性越明顯。對于激勵幅值10 mm的情況，當激勵頻率ω緩慢增加時，振幅沿著曲線上點1、2、3、4、5 變化，并且振幅在曲線上由點3 跳躍到點4，出現了一個激勵頻率對應兩個位移數值解的情況。當激勵頻率ω緩慢減少時，振幅沿著曲線上點5、4、6、2、1 變化，并且振幅在曲線上由點6 跳躍到點2，此時真實的位移解將依賴于系統的初始狀態。兩種情況下均發生了系統特性跳躍的現象，即任何微小的擾動都會導致系統響應在兩個位移解之間跳躍，說明系統特性已經失穩了。通過數值計算結果分析可知，慣組減振器適應的飛行環境振動位移不應超過3 mm。

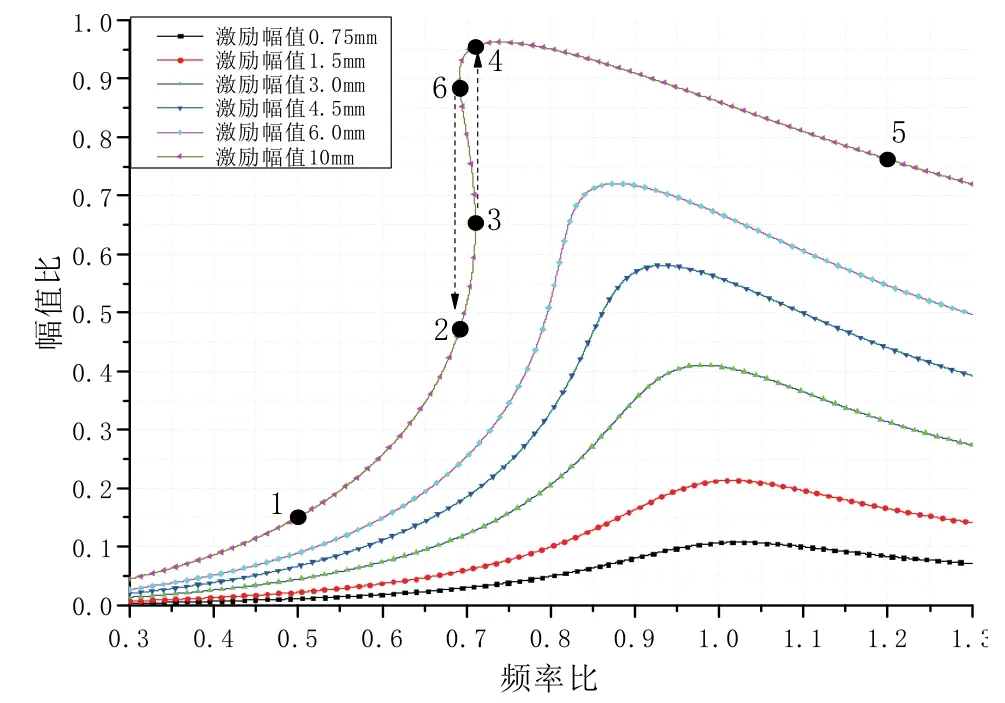
圖8 慣組小系統非線性頻響函數Fig.8 Nonlinear frequency-response functions of inertial navigation system

4 結論

研究了不同激勵幅值對慣組小系統非線性動剛度特性和頻響函數及傳遞特性的影響。基于“三心重合”的設計思想和飛行器的姿態需求，構建了含立方項非線性剛度的慣組小系統非線性動力學方程。采用正弦掃頻激勵的方式獲取慣組小系統傳遞特性，得到了橡膠減振器動剛度受振幅影響的結論，試驗結果驗證了其具有漸軟剛度的非線性特性。掃頻法計算結果與正弦掃頻試驗結果的吻合度達到了96.5%，檢驗了非線性動力學模型的正確性。基于構建模型，采用龍格-庫塔法計算得到的動剛度曲線直觀地表征了減振器的漸進軟化的非線性特性，發現了減振器動剛度存在對激勵幅值和激勵頻率的敏感區域。采用虛弧長延拓法通過頻響函數和傳遞特性的非線性分析預示了高量級振動環境下慣組小系統會出現動力失穩的現象。

本文模型工程應用簡便，對慣組小系統非線性特性的預示具有較高的精度，供飛行器姿控系統設計時參考。針對大過載飛行環境，建議采用預壓縮設計合理調整減振器預壓縮量。預壓縮設計會影響系統的靜平衡位置，通過將坐標系原點選在靜平衡位置就可以簡化系統運動方程，適當調整本文模型參數即可用于相關環境下非線性特性的預示。

飛行器實際飛行時處于一個多自由度激勵的環境，后續建議開展多自由度激勵下慣組小系統非線性特性的研究。