幾何課堂教學有效性的策略研究
——以“圓的對稱性”教學實踐為例
張 戍
(蘇州市吳江區震澤初級中學 江蘇蘇州 215000)
在教授幾何知識的過程中,想要提高幾何課堂教學的有效性,就必須加強學生對幾何圖形探究能力的培養,這有助于增強學生主動探索、親自探究的欲望,促進學生自主求學能力不斷提升;有助于學生更充分地理解和掌握知識,不斷拓展學生的幾何思維能力。另外,及時提供課堂教學的反饋信息,使學生的思維過程在具體操作中顯現出來,讓抽象的公式、定理、法則在實踐中得到驗證,有利于培養學生嚴謹的科學態度[1][2]。
為此,我選擇“圓的對稱性(第一課時)”這節課,分別在初三(1)班和初三(2)班授課,研究如何培養學生的幾何圖形探究能力,從而提高幾何教學的有效性。
第一次教學案例(片段):
在探究“圓心角、弧、弦之間的關系”的過程中,第一步是“嘗試與交流”環節,我先給出一個操作活動,內容如下:
(1)在兩張透明紙片上,分別作半徑相等的⊙O和⊙O'。
(2)在⊙O和⊙O'中,分別作相等的圓心角∠AOB、∠A'O'B',連接AB、A'B'。

(3)將兩張紙片疊在一起,使⊙O和⊙O'重合。
(4)固定圓心,將其中一個圓旋轉某個角度,使得OA和O'A'重合。
我先用多媒體演示此操作過程的動畫,然后提問:在操作的過程中,你發現了哪些相等的量?請和同學交流一下。
學生1:∠AOB=∠A'O'B'
我:對的,這是題目中的已知條件。
學生2:OA=OB=O'A'=O'B'
我:很好,這是同圓和等圓的半徑。還有嗎?
我:非常好,你能想到我們現在所學的圓中的一些量。
我:在同圓中,以上式子是否成立?
學生齊聲回答:成立。
再引導學生得出結論:在同圓或等圓中,相等的圓心角所對的弧相等,所對的弦相等。
第二步是“思考與探索”環節,讓學生思考以下2個問題:
(1)在同圓或等圓中,如果圓心角所對的弧相等,那么它們所對的弦相等嗎?這兩個圓心角相等嗎?你是怎么想的?
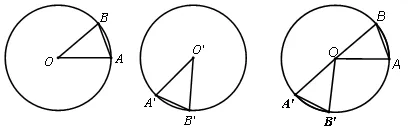
當我讓學生說明時,學生回答不出,最后只能由我說理。
學生歸納結論:在同圓或等圓中,相等的圓心角所對的弧相等,所對的弦相等。
(2)在同圓或等圓中,如果圓心角所對的弦相等,那么它們所對的弧相等嗎?這兩個圓心角相等嗎?你是怎么想的?

理由是在我的引導下回答出來的。
學生歸納結論:在同圓或等圓中,相等的圓心角所對的弧相等,所對的弦相等。
最后在我的提示下,學生歸納“圓心角、弧、弦之間的關系”:
在同圓或等圓中,如果兩個圓心角、兩條弧、兩條弦中有一組量相等,那么它們所對應的其余各組量都分別相等。
第一次課后反思:第一環節中,雖然多媒體的展示能引起學生的興趣,但由于演示過程較快,學生還沒反應過來,演示就已經結束了。而學生在以往的學習中,嘗試幾何題的探索機會較少,課堂上光用多媒體展示操作無法調動學習積極性。因此,要讓學生課前做好準備,課堂上讓學生自己動手去操作及探索。第二環節中,因為學生沒有經歷動手操作,感觀比較抽象,不理解,導致無法回答得出結論的理由,而我急于完成教學任務,不經過啟發,就直接給出了答案。所以,應該增加合作討論環節,促進學生的相互交流與學習,從而調節課堂氣氛,促進學生主動學習。
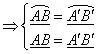
∵∠AOB=∠A'O'B'
∴OB與O'B'重合
此時點A與點A'重合,點B和點B'重合
由于“思考與探索”環節的2個小題的探索與“嘗試與交流”類似,所以我將全班分為兩大組,一組討論第(1)題,另一組討論第(2)題,學生可以自由選擇搭檔進行討論。回答時,我設置了搶答環節。第(1)小題學生搶答如下:
學生1:在同圓或等圓中,如果圓心角所對的弧相等,那么它們所對的弦相等,這兩個圓心角也相等。
此時點A與點A'重合,點B和點B'重合
∴∠AOB=∠A'O'B',AB=A'B'
學生5歸納:在同圓或等圓中,相等的圓心角所對的弧相等,所對的弦相等。
第(2)小題類似于第(1)小題的回答。
我:現在我們來看一下,以上的問題中提到了幾個量?
學生6:3個量,圓心角和它所對的弧及它所對的弦。
我:觀察一下,這3個量的關系。
學生7:在同圓或等圓中,如果兩個圓心角、兩條弧、兩條弦中有一組量相等,那么它們所對應的其余各組量都分別相等。
第二次課后反思:成功之處是,“嘗試與交流”環節,既有多媒體展示,又有學生分組操作并討論,不但激發了學生的興趣,也為課堂添加了活躍的氣氛。其間,我又引導學生說理,這為“思考與探索”環節奠定了基礎,使學生分組討論后能較輕松地回答出“你是怎么想的”。搶答環節既節約了一定的課堂時間,也充分調動了學生的學習積極性。在這節課中,通過操作活動,鍛煉了學生的動手能力;通過探索思考,鍛煉了學生的思維能力;通過嘗試說理,鍛煉了學生的幾何語言表述能力。
不足之處是,由于各個學生的學習能力不同,各個小組操作及探索所花的時間差異較大;自由選擇搭檔時,往往成績好的學生找其他好學生討論,學困生會被“晾”在一邊無人問津。今后可以適當分配小組成員,讓一些好學生帶動學困生,促進學困生的學習參與性。
培養學生幾何圖形探究能力是適應新時代的需要,是培養學生數學能力的一種重要手段,也是提高學生學習數學興趣的一種有效的方法。教學中在培養學生幾何圖形探究能力的時候,教師首先應注意及時指導學生在動手操作中伴以思維和語言的表達,對于動手操作較困難的小組給予引導啟發;其次,在學生發現和感受到一種知識或一種方法后,要組織學生相互交流,擺事實,講道理,進行分析,形成共同認識;最后,指導學生進行總結,形成正確、清晰的數學概念。總之,提高幾何課堂教學的有效性的前提是教師應加強培養學生的幾何圖形探究能力,發展學生的思維,使學生成為學習的主人,成為全面發展的學生[3]。

