淺談等價(jià)無窮小替換的教學(xué)

曾 勇

(重慶工商大學(xué) 重慶 400067)

高等數(shù)學(xué)（微積分）課程的核心包括微分學(xué)、積分學(xué)、級數(shù)等內(nèi)容。這些內(nèi)容都是在“極限”這一重要概念的基礎(chǔ)上建立起來的，所以“極限”在高等數(shù)學(xué)教學(xué)中起著至關(guān)重要的作用。本科階段高等數(shù)學(xué)極限部分的教學(xué)內(nèi)容主要由極限的概念和極限的計(jì)算兩部分組成。在教學(xué)過程中，它們各有側(cè)重。結(jié)合教學(xué)經(jīng)驗(yàn)，本文主要探討極限計(jì)算中等價(jià)無窮小替換的教學(xué)。

一、等價(jià)無窮小的概念

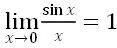
二、常見的等價(jià)無窮小

為了更好地掌握等價(jià)無窮小的概念和應(yīng)用，教學(xué)過程中應(yīng)引導(dǎo)學(xué)生熟記常見的等價(jià)無窮小。例如，當(dāng)時(shí)，我們有如下常見等價(jià)無窮小[1]：

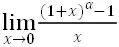
三、等價(jià)無窮小的變式

上述等價(jià)無窮小是最基本的等價(jià)無窮小，在實(shí)際應(yīng)用中，往往需要對上述等價(jià)無窮小作適當(dāng)?shù)淖冃巍Ｒ詘～sinx，x→0為例，粗糙地講，它是說一個(gè)無窮小x2和它本身的正弦sinx2等價(jià)。由此，我們可以得出：x→0時(shí)，無窮小x2和它的正弦sinx2等價(jià)；x→1時(shí)，無窮小x-1和它的正弦sin(x-1)等價(jià)。

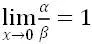
四、等價(jià)無窮小替換定理

我們有如下等價(jià)無窮小替換定理：

解：注意到當(dāng)x→1時(shí)，

lnx=ln(1+x-1)～x-1，arcsin(x-1)～x-1，

雖然一般而言，我們不能替換加減法中的某些因子，但對一些特殊情況，我們?nèi)杂腥缦陆Y(jié)論：

五、結(jié)束語

等價(jià)無窮小替換是極限計(jì)算中的重要方法。通過具體例題的講解有助于學(xué)生厘清該方法應(yīng)用中的各個(gè)要點(diǎn)，對正確使用該方法有重要作用。