似星樹與路的乘積圖的任意可分性

張盼盼, 劉鳳霞, 孟吉翔

(新疆大學(xué) 數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院, 烏魯木齊 830046)

1 引言與預(yù)備知識(shí)

設(shè)圖G=(V,E)是階為n的簡(jiǎn)單圖, 正整數(shù)序列λ=(λ1,λ2,…,λp)是一個(gè)非遞減序列. 如果λ1+λ2+…+λp=n, 則稱λ是G的可允許序列. 如果λ是一個(gè)可允許序列, 且存在對(duì)點(diǎn)集V的一個(gè)劃分(V1,V2,…,Vp), 使得每個(gè)Vi導(dǎo)出一個(gè)階為λi的G的連通子圖, 則稱λ是G的可實(shí)現(xiàn)序列, 且(V1,V2,…,Vp)是序列λ在G中的實(shí)現(xiàn), 每個(gè)子圖G[Vi]稱為圖G的λi分支. 如果每個(gè)可允許序列都是可實(shí)現(xiàn)的, 則稱G是任意可分圖(簡(jiǎn)稱AP圖或AVD圖)[1]. 如果圖G含一條Hamilton路, 則稱圖G為可跡圖. 顯然, 每個(gè)可跡圖都是任意可分圖. 當(dāng)圖G的階為偶數(shù)時(shí),G有完美匹配等價(jià)于序列(2,2,…,2)是G的可實(shí)現(xiàn)序列； 當(dāng)圖G的階為奇數(shù)時(shí),G有幾乎完美匹配等價(jià)于序列(1,2,…,2)是G的可實(shí)現(xiàn)序列. 因此, 任意可分圖一定有完美匹配或幾乎完美匹配, 從而一個(gè)圖有完美匹配或者幾乎完美匹配的必要條件是該圖為任意可分圖.

如果圖G的生成樹是任意可分圖, 則圖G是任意可分圖. Horňk等[2]證明了如果樹T是任意可分的, 則T的最大度至多為6, 并且提出了任意可分樹的最大度至多為4的猜想. 該猜想被Barth等[3]證明, 得到了任意可分樹的最大度至多為4, 且每個(gè)4度頂點(diǎn)與一個(gè)葉子點(diǎn)相鄰的結(jié)論. Cichacz等[4]刻畫了4個(gè)葉子點(diǎn)的毛毛蟲樹的任意可分性, 并展示了最大度為3或4的兩類任意可分樹. Marczyk[5]證明了對(duì)階為n的連通圖G, 當(dāng)獨(dú)立數(shù)至多為n/2, 且任意一對(duì)不相鄰頂點(diǎn)的度和至少為n-3時(shí), 圖G是任意可分圖或者同構(gòu)于兩個(gè)例外圖. Horňk等[6]證明了對(duì)階數(shù)n≥20的連通圖G, 任意兩個(gè)不相鄰頂點(diǎn)的度和至少為n-5, 則G有完美匹配或幾乎完美匹配. Baudon等[7]提出了任意可分圖和可跡圖的笛卡爾積圖是任意可分圖的猜想, 證明了可跡圖的頂點(diǎn)數(shù)至多為4時(shí)猜想成立, 并證明了當(dāng)兩個(gè)任意可分圖中至少有一個(gè)階數(shù)至多為4時(shí), 這兩個(gè)任意可分圖的笛卡爾積圖也是任意可分圖. 文獻(xiàn)[8]證明了樹T的最大度至多為l+1時(shí), 如果T中有一條包含所有(l+1)度頂點(diǎn)的路, 則T□Cl是任意可分圖. 此外, 文獻(xiàn)[9-11]研究了樹的笛卡爾積圖的相關(guān)性質(zhì).

本文將兩個(gè)圖G和H的乘積圖記為G??H, 其頂點(diǎn)集

V(G??H)={(g,h)|g∈V(G)且h∈V(H)},

邊集

E(G??H)={(g,h)(g′,h′)|gg′∈E(G)且hh′∈E(H)或gg′∈E(G)且h=h′}.

用S=S(a1,a2,…,at,b1,b2,…,bs)表示最大度為t+s的似星樹, 設(shè)d(v)=t+s, 則

S-{v}=Pa1∪Pa2∪…∪Pat∪Pb1∪Pb2∪…∪Pbs,

其中Pai=vi1vi2…viai,Pbj=v(t+j)1v(t+j)2…v(t+j)bj, 且ai(1≤i≤t)是奇數(shù),bj(1≤j≤s)是偶數(shù),

本文給出在t和s的不同取值下, 乘積圖S??Pl的任意可分性.

2 主要結(jié)果

設(shè)S=S(a1,a2,…,at,b1,b2,…,bs)是最大度為t+s的似星樹, 假設(shè)t+s≥2. 設(shè)G=S??Pl, 其中|Pl|=l≥2, 圖Sp是S在G中的第p個(gè)拷貝, 其對(duì)應(yīng)的點(diǎn)集為

其中vp是Sp的最大度點(diǎn). 似星樹S(a,b,c)是階為1+a+b+c, 由一個(gè)3度頂點(diǎn)連接3條長(zhǎng)分別為a,b,c的不交路的圖. 本文將序列(λ1,…,λ1,…,λp,…,λp)記為((λ1)k1,…,(λp)kp), 對(duì)i∈{1,2,…,p},λi出現(xiàn)ki次. 兩個(gè)正整數(shù)a和b的最大公因子記為gcd(a,b).

命題1對(duì)于圖G及其可允許序列λ=(λ1,λ2,…,λp), 存在(V1,V2,…,Vm), 滿足

|V1|=λ1, |V2|=λ2, …, |Vm|=λm,

且G[Vj]連通, 其中1≤j≤m, 如果

V-V1-V2-…-Vm=V0,

G[V0]有一條Hamilton路, 則必存在Vm+1,Vm+2,…,Vp, 滿足|Vi|=λi且G[Vi]連通, 其中m+1≤i≤p. 因此, 圖G的可允許序列λ=(λ1,λ2,…,λp)是可實(shí)現(xiàn)的.

引理1(Tutte’s定理)[12]設(shè)圖G是階為偶數(shù)的連通圖, 則圖G有完美匹配當(dāng)且僅當(dāng)對(duì)所有的點(diǎn)子集S?V, 均有o(G-S)≤|S|.

引理2[13]設(shè)圖G是階為奇數(shù)的連通圖, 則圖G有幾乎完美匹配當(dāng)且僅當(dāng)對(duì)所有的點(diǎn)子集S?V, 均有o(G-S)≤|S|+1.

引理3[1,14]設(shè)圖G是似星樹S(1,a,b), 且1≤a≤b, 則圖G是任意可分圖當(dāng)且僅當(dāng)

gcd(a+1,b+1)=1.

定理1設(shè)S=S(a1,a2,…,at,b1,b2,…,bs)是似星樹, 其中t≥2, 則圖S??Pl不是任意可分圖.

證明: 設(shè)G=S??Pl, 為證明圖G不是任意可分圖, 只需找到一個(gè)不可實(shí)現(xiàn)的序列, 下面證明圖G不含完美匹配或幾乎完美匹配.

取G的獨(dú)立集

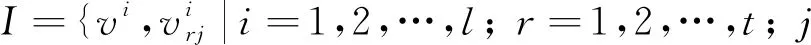
圖G-I的奇分支數(shù)為o(G-I), 如圖1(A)所示. 設(shè)m=a1+a2+…+at,Si是S在圖G中的第i個(gè)拷貝, 則有

因?yàn)閠≥2, 則o(G-I)-|I|≥2. 由引理1和引理2知, 圖G不含完美匹配或幾乎完美匹配. 因此, 圖G不是任意可分圖.

定理2設(shè)S=S(a1,a2,…,at,b1,b2,…,bs)是似星樹, 其中t=0, 則圖S??Pl不是任意可分圖.

證明: 設(shè)G=S??Pl, 由t+s≥2,t=0知s≥2, 與定理1的證明類似. 令圖G的獨(dú)立集

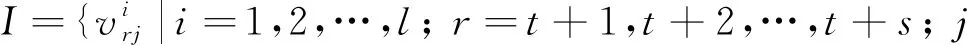
o(G-I)是圖G-I的奇分支數(shù), 如圖1(B)所示. 設(shè)m=b1+b2+…+bs,Si是S在圖G中的第i個(gè)拷貝. 顯然,G-I是孤立點(diǎn), 則有

由引理1和引理2知, 圖G不含完美匹配或幾乎完美匹配. 因此, 圖G不是任意可分圖.

定理1和定理2分別討論了t≥2和t=0的情形, 下面討論t=1的情形.

定理3設(shè)S=S(a1,a2,…,at,b1,b2,…,bs)是似星樹, 其中t=1,s=1, 則圖S??Pl是任意可分圖.

圖1 圖G的拷貝Si

證明: 設(shè)G=S??Pl, 當(dāng)l為偶數(shù)時(shí), 可找到圖G中的一條Hamilton路P, 如圖2所示, 即

圖2 圖S(a1,b1)??Pl(l為偶數(shù))

當(dāng)l為奇數(shù)時(shí), 同理可找到圖G中的一條Hamilton路. 因此, 圖G是任意可分圖.

定理4設(shè)S=S(a1,a2,…,at,b1,b2,…,bs)是似星樹, 其中t=1,s=2, 即S=S(a1,b1,b2), 則圖S??Pl是任意可分圖.

證明: 下面僅討論l為奇數(shù)的情形, 當(dāng)l為偶數(shù)時(shí)同理可證. 令

1) 如圖3所示,a1=1. 此時(shí), 設(shè)

則

圖3 圖S(1,b1,b2)??Pl

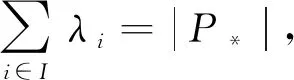
① 當(dāng)r=1時(shí), 令Vr={vl-1}.

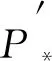
2) 如圖4所示,a1≥3. 此時(shí), 令

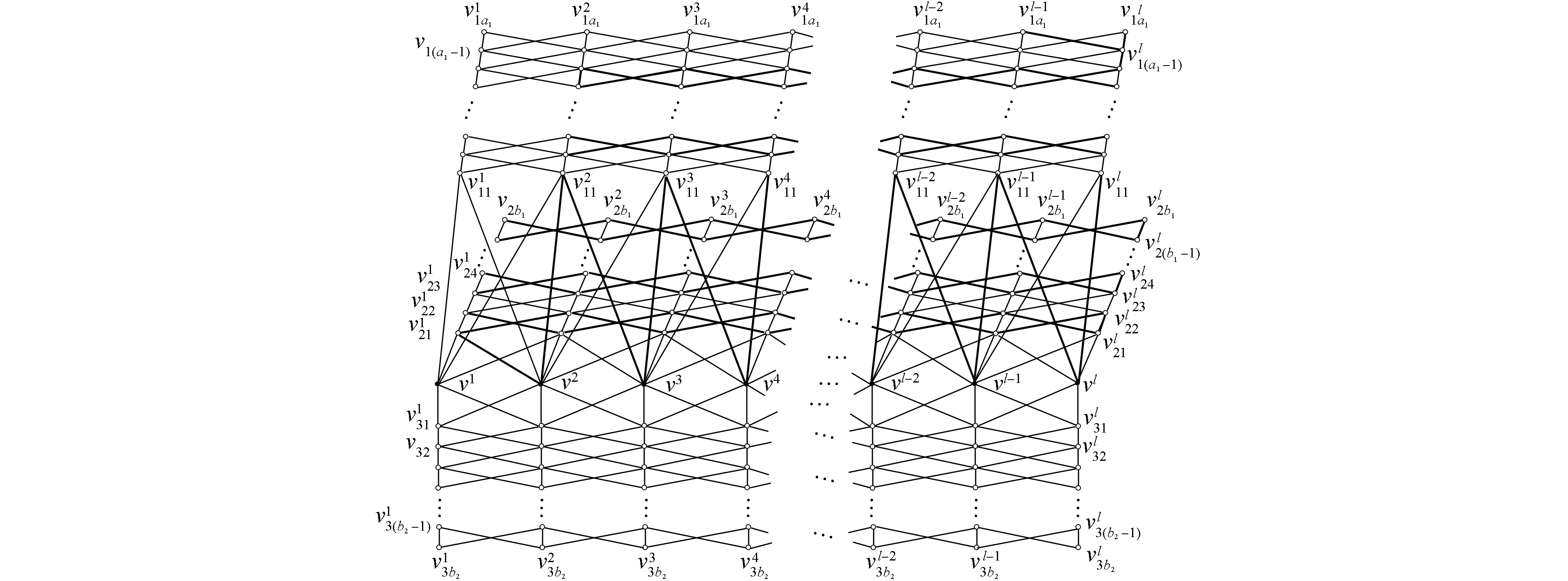
圖4 圖S(a1,b1,b2)??Pl

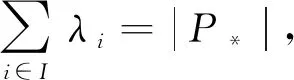
gcd(2,b1l+(a1-1)(l-1)+1)=1.

由引理3, 似星樹S(1,1,b1l+(a1-1)(l-1))是任意可分圖. 因此, 序列λ在圖G中是可實(shí)現(xiàn)的.

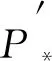
因此, 序列λ是圖G的可實(shí)現(xiàn)序列.

定理5設(shè)S=S(a1,a2,…,at,b1,b2,…,bs)是似星樹, 其中t=1,s≥3, 且Δ(S)≥l+2. 如果b1=b2=…=bs, 則圖S??Pl不是任意可分圖.

證明: 設(shè)G=S??Pl, |G|=n,Δ(S)=k. 令q=b1=b2=…=bs且b=ql, 則

n=(k-1)b+(a1+1)l.

考慮到圖G-{v1,v2,…,vl}連通分支的階為a1l和b, 下面分兩種情形討論.

1) 若a1

c=n-l(b+1)=(k-1)b+a1l-bl>a1l.

若λ是G的可實(shí)現(xiàn)序列, 則每個(gè)b+1分支必須包含一個(gè)點(diǎn)vi,i∈{1,2,…,l}. 因?yàn)閏≥a1l+1, 故c分支必包含一個(gè)點(diǎn)vi,i∈{1,2,…,l}, 共需(l+1)個(gè)點(diǎn), 與l=|{vi|i=1,2,…,l}|矛盾.

2) 若a1>b1, 則如果k=l+2, 可考慮G的可允許序列λ=((b+1)l,a1l+1,c), 其中c=b-1. 如果k>l+2, 可考慮G的可允許序列λ=((b+1)l+1,a1l+1,c), 其中c=(k-l-2)b-2.

在這兩種情形下, 每個(gè)b+1分支必包含一個(gè)點(diǎn)vi,i∈{1,2,…,l}, 每個(gè)a1l+1分支也必包含一個(gè)點(diǎn)vi,i∈{1,2,…,l}, 與l=|{vi|i=1,2,…,l}|矛盾, 故λ不是G的可實(shí)現(xiàn)序列, 圖S??Pl不是任意可分圖.