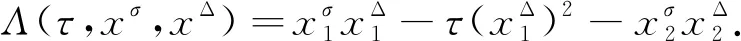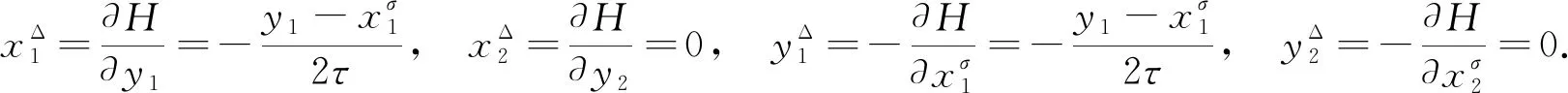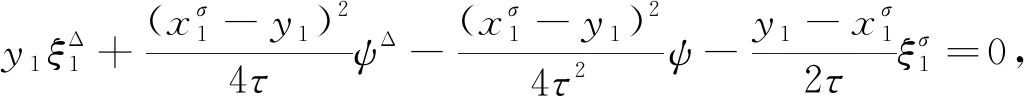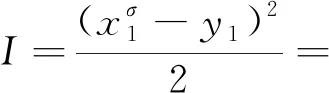事件空間中時標上Hamilton系統的Noether對稱性定理
施玉飛, 張 毅
(1. 蘇州科技大學 數學科學學院, 江蘇 蘇州 215009; 2. 蘇州科技大學 土木工程學院, 江蘇 蘇州 215011)
時標上的微積分理論[1]統一了連續分析和離散分析, 可揭示連續與離散現象的內在聯系和本質區別. Bohner[2]研究了時標上的變分問題, 給出了時標Euler-Lagrange方程; Bartosiewicz等[3]建立了時標上的Noether定理. 目前, 關于Noether定理及其應用的研究已取得許多成果[4-7], 但關于時標上Noether理論的研究文獻報道較少. Cai等[8]研究了時標上非保守非完整系統的Noether對稱性; 文獻[9-11]分別建立了時標上Hamilton系統、 Birkhoff系統、 時滯系統的Noether定理. 本文進一步討論事件空間中時標上Hamilton系統的Noether對稱性與守恒量, 給出事件空間中時標Hamilton系統的Noether對稱性定理.
1 時標微積分及基本性質
設 T是一時標, 定義向前跳躍算子σ: T→T為σ(t)=inf{s|s>t,s∈T}, 向后跳躍算子ρ: T→T為ρ(t)=sup{s|s 假設函數f: T→, 令t∈Tk, 如果給定任一ε>0, 存在δ>0, 使得對所有的s∈U,U=(t-δ,t+δ)∩T, 均有 |[f(σ(t))-f(s)]-fΔ(t)[σ(t)-s]|≤ε|σ(t)-s|, (1) 對于時標微積分, 下列運算公式[12]成立: 其中函數β(t): [r,s]∩T→單調遞增且和表示定義在變換后的時標上. 引理1(時標上Dubois-Reymond引理)[12]令g∈Crd,g: [a,b]→n, 則對所有的且η(a)=η(b)=0,gT(t)ηΔ(t)Δt=0均成立當且僅當g(t)=c, 其中常數c∈n. (8) 則事件空間中時標Hamilton原理為 (9) 且滿足關系 (10) 端點條件為 δxα|τ=a=δxα|τ=b=0,α=1,2,…,n+1, (11) 其中:a,b∈T且a 引進事件空間中時標上的廣義動量和Hamilton函數: (12) 則式(9)可表示為 (13) 對Hamilton作用量 (14) 求變分, 得 (15) 由式(3)和式(11), 有 因此 (17) 將式(12)第二個等式的兩邊對yα求偏導數, 得 (18) 將方程(18)代入式(17), 得 (19) 由Dubois-Reymond引理, 得 (20) 對式(20)兩邊求Δ-導數, 得 (21) 聯立方程(18)和(21), 得 (22) 此即為事件空間中時標Hamilton正則方程. 文獻[3-4]給出了證明Noether對稱性定理的不同方法. 本文采用時間重新參數化方法建立并證明事件空間中時標上Hamilton系統的Noether對稱性定理, 證明過程分兩步. 1) 考慮參數τ不變的特殊無限小變換: (23) 定義1對任意子區間[τa,τb]?[a,b], 其中τa,τb∈T, 如果成立 (24) 則稱這種不變性為事件空間中時標上Hamilton系統(22)在無限小變換(23)下的Noether對稱性. 定理1如果參數τ不變的特殊無限小變換(23)相應于事件空間中時標上Hamilton系統(22)的Noether對稱性, 則對任意τ∈[a,b], 成立 (25) 證明: 由于對任意的[τa,τb]?[a,b], 式(24)成立, 因此有 (26) 將式(23)代入式(26), 得 (27) 將式(27)對ε求導, 并令ε=0, 即可得式(25). 證畢. 定理2如果參數τ不變的特殊無限小變換(23)相應于事件空間中時標上Hamilton系統(22)的Noether對稱性, 則 I=yαξα=常數 (28) 是該系統的Noether守恒量. 證明: 由正則方程(22)及式(25), 可得 于是守恒量式(28)成立. 證畢. 2) 考慮參數τ變更的一般無限小變換: (29) 設映射β為 τ→β(τ)=τ+εψ(τ,xi,yi)+o(ε), (30) (31) 定義2對任意子區間[τa,τb]?[a,b], 其中τa,τb∈T, 如果成立 (32) 則稱這種不變性為事件空間中時標上Hamilton系統(22)在無限小變換(29)下的Noether對稱性. 定理3如果參數τ變更的一般無限小變換(29)相應于事件空間中時標上Hamilton系統(22)的Noether對稱性, 則對任意τ∈[a,b], 成立 (33) 證明: 由式(32), 有 由于式(34)對任意積分區間成立, 因此有 (35) 將式(35)對ε求導, 得 (36) 在式(36)中令ε=0, 有 再考慮到式(22), 即可得式(33). 證畢. 定理4如果參數τ變更的一般無限小變換(29)相應于事件空間中時標上Hamilton系統(22)的Noether對稱性, 則 (37) 是該系統的Noether守恒量. 證明: 令 (38) 其中τ∈[a,b],x,v,p∈n+1,s,r∈,r≠0. 當s(τ)=τ時, 可得 (39) (40) 其中, (41) 由定義2, 當s(τ)=τ時, 有 注意到當s(τ)=τ時, 有 (44) 是系統的Noether守恒量. 由于 (45) 因此當s(τ)=τ時, 有 (47) (48) 將式(47),(48)代入式(44), 可得守恒量式(37). 證畢. I=yαξα-Hψ=常數. (49) 當 T=h,h>0時, 有σ(τ)=τ+h,μ(τ)=h, 則由式(37)有 (50) 式(49)和式(50)是事件空間中連續和離散情形下的經典Noether守恒量. 當 T=且τ=t時, 由式(37)有 I=pαξα-Hψ=常數, (51) 式(51)與文獻[4]結果一致. 定理2和定理4是本文得到的事件空間中時標上Hamilton系統的Noether對稱性定理. 事件空間中經典Hamilton系統的Noether對稱性定理[4]和時標上Hamilton系統的Noether對稱性定理[9]均為其特例. 考慮位形空間中Lagrange函數 L(t,qσ,qΔ)=t-qσqΔ, (52) 設參數τ定義在時標 T={2n|n∈}∪{0}上. 由σ(τ)和μ(τ)的定義, 可得 σ(τ)=2τ,μ(τ)=τ. (53) 由式(52)和式(8)可得 (54) 再由式(12)有 (55) 于是由式(22)和式(55), 可得時標Hamilton正則方程為 (56) 根據式(33), 有 (57) 方程(57)的解為 ψ=τ,ξ1=0, (58) 因此由定理4可得 (59) 式(59)是系統的Noether守恒量. 事件空間中時間和廣義坐標地位相同, 因而參數選取更靈活, 并且(n+1)個參數方程中已經包含了系統的能量方程, 因此研究事件空間動力學具有重要意義. 本文建立了事件空間中時標Hamilton原理, 導出了時標Hamiltom正則方程, 并建立及證明了事件空間中時標上Hamilton系統的Noether對稱性定理.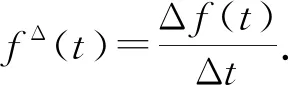
2 事件空間中時標Hamilton正則方程
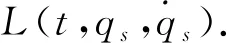
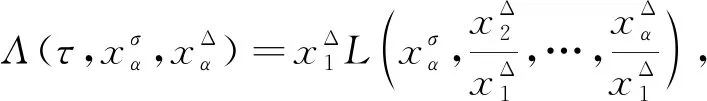
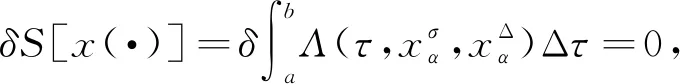

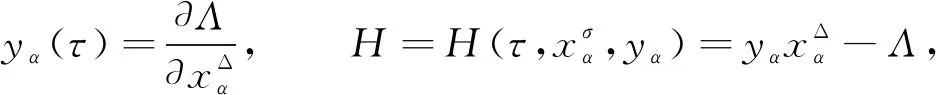
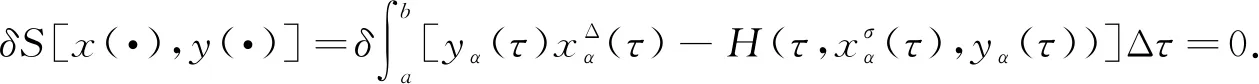

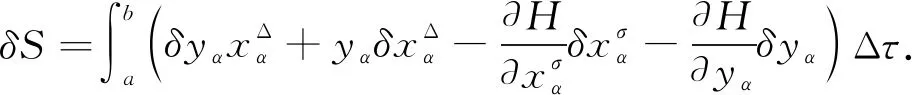
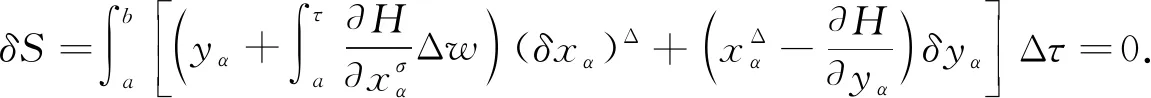
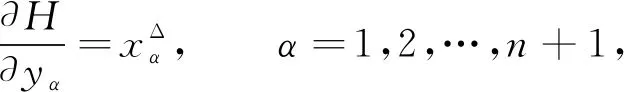
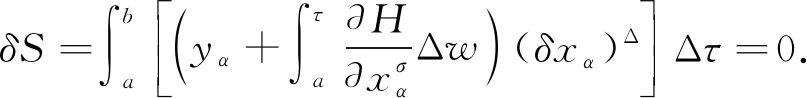
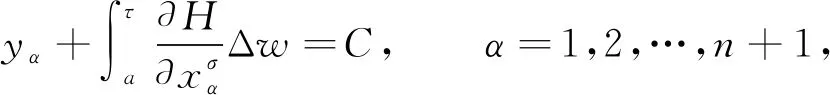
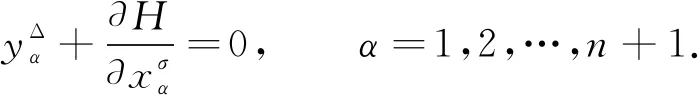
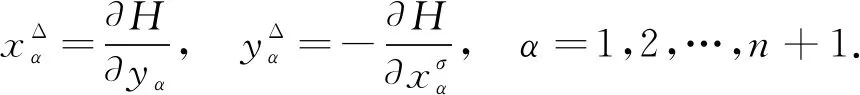
3 主要結果
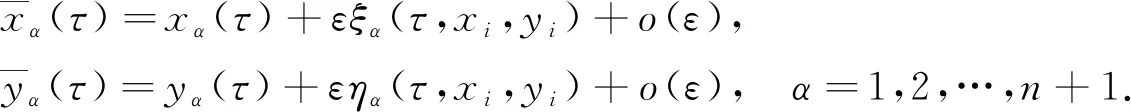
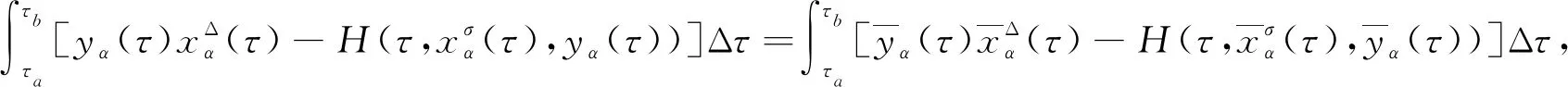
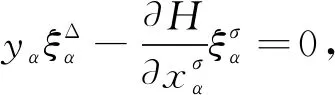
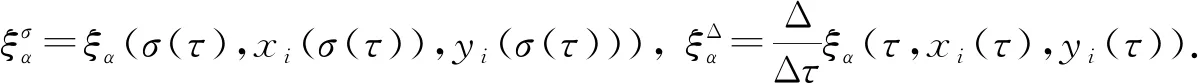
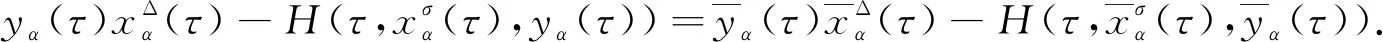
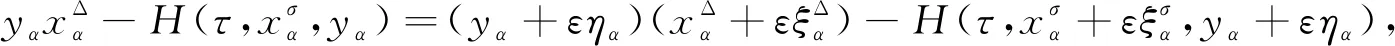
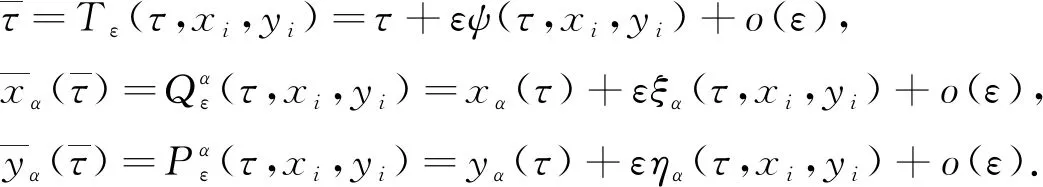
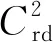
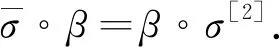
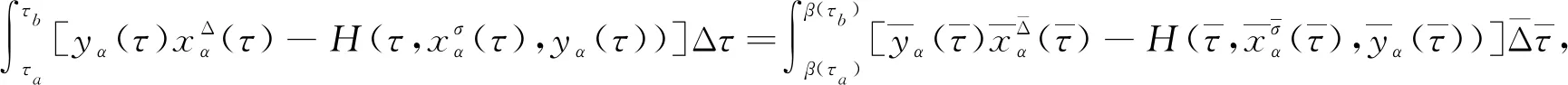
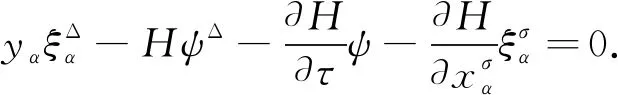
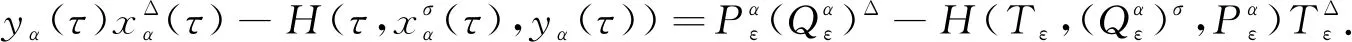
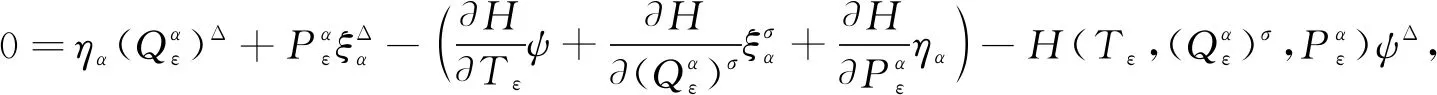
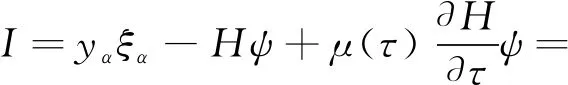
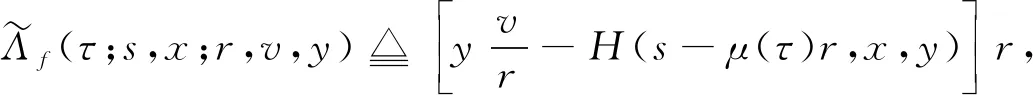
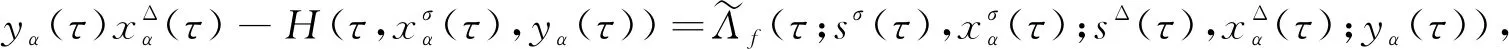
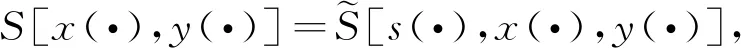
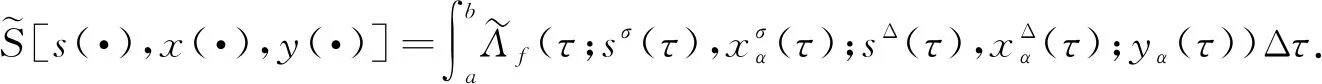
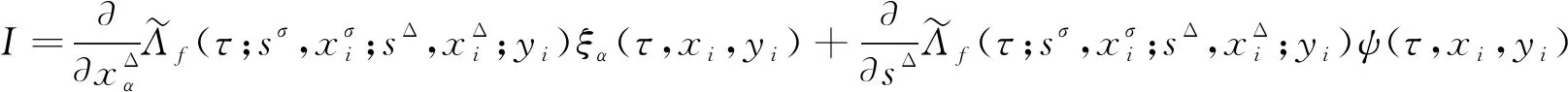
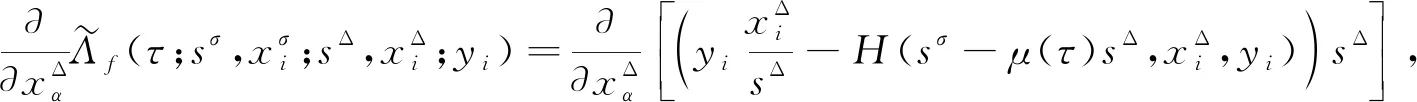
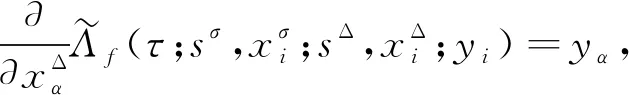
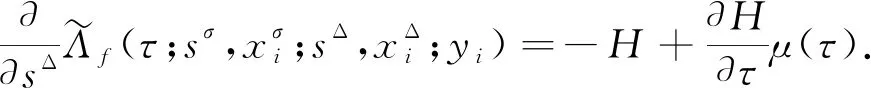
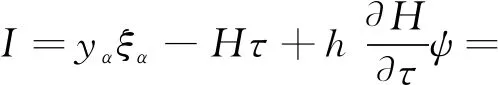
4 算 例