三角代數(shù)上的Jordan零點(diǎn)高階ξ-Lie可導(dǎo)映射

柳 靜, 張建華

(陜西師范大學(xué) 數(shù)學(xué)與信息科學(xué)學(xué)院, 西安 710119)

則{φn}n∈是一個高階導(dǎo)子, 其中[U,V]ξ=UV-ξVU為ξ-Lie積, U°V=UV+VU為Jordan積. 并得到套代數(shù)上Jordan零點(diǎn)高階ξ-Lie可導(dǎo)映射的具體形式.

1 引言與預(yù)備知識

設(shè)A是數(shù)域F上含單位元的代數(shù),U,V∈A. 給定ξ,ζ∈F, 稱[U,V]ξ=UV-ξVU和U°V=UV+VU分別為U和V的ξ-Lie積與Jordan積. 設(shè)φ: A→A是線性映射, {φn}n∈: A→A是一列線性映射(φ0=idA為恒等映射). 如果對任意U,V∈A及n∈, 有

則稱{φn}n∈是A上的高階導(dǎo)子. 如果對任意U,V∈A, 有

φ([U,V]ξ)=[φ(U),V]ξ+[U,φ(V)]ξ,

(1)

則稱φ是A上的ξ-Lie導(dǎo)子. 如果對任意U,V∈A且[U,V]ζ=0有式(1), 則稱φ是A上的ζ-Lie零點(diǎn)ξ-Lie可導(dǎo)映射. 特別地, 當(dāng)ζ=-1,0,1時,ζ-Lie零點(diǎn)ξ-Lie可導(dǎo)映射分別為Jordan零點(diǎn)ξ-Lie可導(dǎo)映射、 零點(diǎn)ξ-Lie可導(dǎo)映射、 Lie零點(diǎn)ξ-Lie可導(dǎo)映射. 如果對任意U,V∈A及n∈, 有

(2)

則稱{φn}n∈是A上的高階ξ-Lie導(dǎo)子. 如果對任意U,V∈A及n∈且U°V=0有式(2), 則稱{φn}n∈是A上的Jordan零點(diǎn)高階ξ-Lie可導(dǎo)映射.

目前, 關(guān)于算子代數(shù)上滿足某種條件的可導(dǎo)映射和高階可導(dǎo)映射的研究已得到廣泛關(guān)注, 并取得許多成果[1-10]. 例如: 文獻(xiàn)[1]證明了三角代數(shù)上互逆元處的高階ξ-Lie可導(dǎo)映射是高階導(dǎo)子; 文獻(xiàn)[2]研究了三角代數(shù)上Jordan積為冪等元處的高階ξ-Lie 可導(dǎo)映射, 并得到了套代數(shù)上該類高階ξ-Lie可導(dǎo)映射的具體形式; 文獻(xiàn)[3]刻畫了三角代數(shù)上交換零點(diǎn)ξ-Lie高階可導(dǎo)映射; 文獻(xiàn)[4]研究了三角代數(shù)上的Jordan零點(diǎn)ξ-Lie可導(dǎo)映射, 并給出了其結(jié)構(gòu). 基于此, 本文討論三角代數(shù)上的Jordan零點(diǎn)高階ξ-Lie可導(dǎo)映射.

設(shè)A和B是實(shí)或復(fù)數(shù)域F上含單位元的代數(shù), M是(A,B)-忠實(shí)雙邊模. 在通常的矩陣運(yùn)算下, 稱

為F上三角代數(shù). 設(shè)U是三角代數(shù)且Z(U)表示其中心, 則由文獻(xiàn)[5]中性質(zhì)3知

設(shè)I是U的單位元,IA和IB分別是A和B的單位元. 記

U11=P1UP1, U12=P1UP2, U22=P2UP2.

顯然, 三角代數(shù)U被分解為U=U11+U12+U22且U12是(U11,U22)-忠實(shí)雙邊模.

2 主要結(jié)果

引理1對任意n∈, 有:

1)φn(I)=P1φn(I)P1+P2φn(I)P2∈Z(U );

2) 對任意冪等元P∈U, 有Pφn(P)P=Pφn(I)=φn(I)P且(I-P)φn(P)(I-P)=0.

證明: 對任意冪等元P∈U, 由P°(I-P)=0得

對式(3)分別左乘P、 右乘P, 得

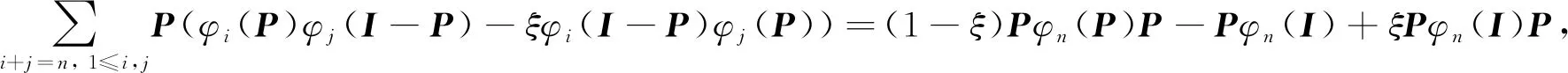
(4)

(5)

由文獻(xiàn)[4]中引理2.1和斷言5可知, 如果ξ≠1， 則對任意冪等元P∈U, 有

φ1(I)=P1φ1(I)P1+P2φ1(I)P2∈Z(U ),

Pφ1(P)P=Pφ1(I)=φ1(I)P,

(I-P)φ1(P)(I-P)=0.

假設(shè)當(dāng)1≤k

φk(I)=P1φk(I)P1+P2φk(I)P2∈Z(U ),

Pφk(P)P=Pφk(I)=φk(I)P,

(I-P)φk(P)(I-P)=0.

則式(4)和式(5)的左邊分別為

表明式(4)和(5)左邊相等. 從而由式(4)和式(5)右邊相等及ξ≠0,1可知, 對任意冪等元P∈U, 均有

Pφn(P)P=Pφn(I)=φn(I)P.

(6)

于是

Pφn(I-P)P=0,

(7)

Pφn(I)(I-P)=0.

(8)

在式(7)中用I-P替換P, 則對任意冪等元P∈U, 有

(I-P)φn(P)(I-P)=0.

在式(8)中取P=P1, 則P1φn(I)P2=0, 從而

φn(I)=P1φn(I)P1+P2φn(I)P2.

(9)

對任意U12∈U12, 顯然P1+U12是U中的冪等元, 從而由式(6)得

(P1+U12)φn(I)=φn(I)(P1+U12),

φn(I)P1=P1φn(I).

于是對任意U12∈U12, 有U12φn(I)=φn(I)U12. 又由式(9), 有

φn(I)=P1φn(I)P1+P2φn(I)P2∈Z(U).

證畢.

引理2對任意n≥1, 有

φn(U12) ?U12,φn(P1),φn(P2)∈U12,φn(I)=0.

證明: 由文獻(xiàn)[4]中斷言7知,

φ1(U12)?U12,φ1(P1),φ1(P2)∈U12,φ1(I)=0.

假設(shè)當(dāng)1≤k

對式(10)分別左右兩邊同乘P1和P2, 并由ξ≠0及U的2-無擾性, 可得

P1φn(U12)P1=P2φn(U12)P2=0.

表明φn(U12)?U12. 對式(10)左乘P1、 右乘P2, 并由ξ≠-1及引理1可得

φn(I)U12=U12φn(I)=0.

于是P1φn(I)P1=P2φn(I)P2=0, 從而由引理1得

φn(I)=0,P1φn(P1)P1=P2φn(P1)P2=0.

因此φn(P1),φn(P2)∈U12. 證畢.

引理3對任意n≥1, 有

φn(U11)?U11+U12,φn(U22)?U12+U22.

證明: 由文獻(xiàn)[4]中斷言8知, 當(dāng)n=1時,φ1在U上是導(dǎo)子, 從而φ1(U11)?U11+U12. 假設(shè)當(dāng)1≤k

對任意U11∈U11, 因?yàn)镻2°U11=0, 所以由歸納假設(shè)可得

又因?yàn)棣巍?, 于是P2φn(U11)P2=0. 因此φn(U11)?U11+U12.

同理, 對任意U22∈U22, 有φn(U22)?U12+U22. 證畢.

引理4對任意n∈,U11∈U11,U22∈U22, 有

證明: 由于U11°U22=0, 由引理3有

引理5對任意n∈,U11∈U11,V12,U12∈U12,V22∈U22, 有:

證明: 1) 由于(U11-U11V12)°(V12+P2)=0, 由引理2～引理4得

從而

2) 同理, 由(U12+P1)°(V22-U12V22)=0及引理2～引理4可得

證畢.

引理6對任意U11,V11∈U11,V12∈U12,U22,V22∈U22, 有：

由引理5中1)及歸納假設(shè)知, 一方面有

另一方面, 有

比較式(11)和式(12), 得

進(jìn)而由U12的忠實(shí)性, 得

(13)

下面證明

對任意U11∈U11, 由于U11°P2=0, 由引理2和引理3可得

從而可得

(14)

同理, 對任意U22∈U22, 有

(15)

再由引理3、 式(14)及歸納假設(shè)知, 對任意U11,V11∈U11, 有

因此可得

(16)

進(jìn)而由式(13),(16)及引理3有

2) 同理, 對任意U22,V22∈U22, 有

證畢.

定理1設(shè)U=Tri(A,M,B)是一個2-無擾的三角代數(shù), {φn}n∈是U上的Jordan零點(diǎn)高階ξ-Lie可導(dǎo)映射(ξ≠0,±1), 則{φn}n∈是U上的高階導(dǎo)子.

證明: 對任意U,V∈U, 有U=U11+U12+U22,V=V11+V12+V22, 其中Uij,Vij∈Uij(1≤i≤j≤2). 于是, 由引理2～引理6得

即{φn}n∈是U上的高階導(dǎo)子. 證畢.

設(shè)H是實(shí)或復(fù)數(shù)域F上的Hilbert空間, B(H )表示H上的全體有界線性算子, H上的套N是一簇包含H和{0}的全序閉子空間, 且在任意交和任意閉線性張運(yùn)算下封閉, 套N相應(yīng)的套代數(shù)為Alg N ={T∈B(H ):TN?N, ?N∈N }. 由定理1, 有如下結(jié)論:

推論1設(shè)N是Hilbert空間H上的一個非平凡套, Alg N是相應(yīng)的套代數(shù), {φn}n∈是Alg N上的Jordan零點(diǎn)高階ξ-Lie可導(dǎo)映射(ξ≠0,±1), 則{φn}n∈是Alg N上的高階導(dǎo)子.