基于微觀機制的復雜應力狀態下鋼材韌性斷裂行為研究

葉繼紅，范志鵬

(1. 江蘇省土木工程環境災變與結構可靠性重點實驗室(中國礦業大學)，徐州 221116；2. 徐州市工程結構火安全重點實驗室(中國礦業大學)，江蘇，徐州 221116；3. 東南大學土木工程學院，江蘇，南京 211189)

目前，金屬材料斷裂預測方法總體可分為兩類：一類為傳統斷裂力學方法[1]；另一類為基于微觀機制的斷裂預測方法[2]。由于傳統斷裂力學方法是基于材料中已存在宏觀裂紋假定，其不適用于無初始缺陷的韌性斷裂問題。基于微觀機制的斷裂預測方法是根據金屬材料的微觀機理建立力學模型，其認為引起材料斷裂的兩種主要微觀機理為空穴聚合型斷裂機理及局部剪切帶的形成。

空穴聚合型斷裂機理是鋼材韌性斷裂的常見形式，空穴演化過程通常分為三個階段：空穴形核、空穴擴張和空穴貫通[3-4]，如圖1 所示。金屬材料在低應力三軸度下斷口部位會呈現剪切型微觀斷裂機理[5-7]，與脆性斷裂形式不同的是材料在形成剪切型斷裂前可承受明顯的塑性變形。如圖2所示，在低應力三軸度應力狀態下，材料中空穴在形核后不僅沒有擴張的趨勢，相反空穴體積會隨著塑性應變的增大而逐漸變小，直至突然壓扁形成塑性剪切帶[8]，引發剪切斷裂。

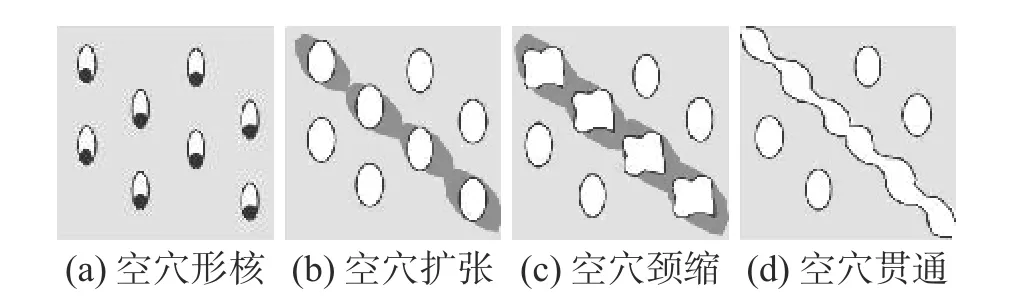
圖 1 空穴形核、擴張及貫通機理Fig. 1 The mechanism of void nucleation,expansion and penetration

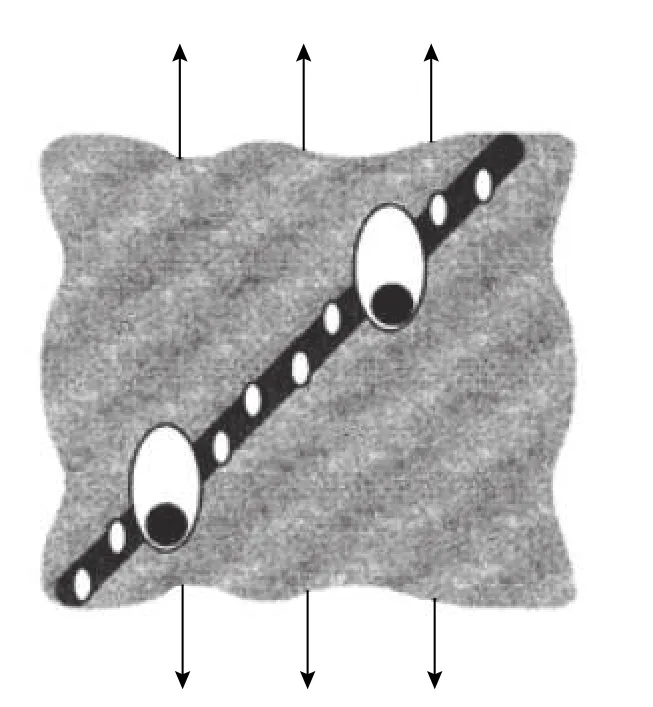
圖 2 塑性剪切帶Fig. 2 Plastic shear band

基于微觀機制的斷裂預測模型在預測鋼材延性斷裂上具有明顯優勢，如Rice-Tracey 模型[9]、VGM 模型和SMC 模型[10]、GTN 模型[11]等，近年來這些模型開始廣泛應用于鋼材韌性斷裂破壞研究。廖芳芳等[12-13]進行了多組Q345 鋼材切口圓棒單軸拉伸試驗，并采用校準后的VGM 模型和SMCS 模型對Q345 鋼焊接節點的斷裂行為進行預測，預測結果較好；黃學偉等[14]采用GTN 模型對梁柱焊接節點的斷裂行為進行預測，得到了良好的預測結果。上述斷裂模型應用于應力三軸度較高的鋼材斷裂行為預測時可獲得較高的精度，但應用于以剪切斷裂為主的低應力三軸度區時精度卻相對很低，數值模擬結果離散型也較大。其原因是上述斷裂模型沒有考慮羅德角的影響，在低應力三軸度區的金屬材料韌性斷裂應變不再符合高應力三軸度區的拉伸斷裂趨勢。

為了改進上述模型的局限性，馬昕煦等[15]在Rice-Tracey 模型基礎上提出了一個羅德角依賴型的斷裂模型，并將該模型用于鋼管節點斷裂預測分析，能夠準確模擬鋼管節點的剪切型斷裂行為；黃學偉等[16]在VGM 模型中引入羅德參數的影響提出LVGM 模型，并用校準后的LVGM 模型對一組Q235B 鋼節點試件進行斷裂預測，預測結果與試驗結果吻合良好。上述改進后的斷裂模型雖然考慮了羅德角對材料斷裂性能的影響，但仍缺乏微觀斷裂機理支持。閆伸[8]提出了考慮空穴形核的剪切斷裂模型VNISFM 模型，并進行了多組材性試驗驗證了該斷裂模型，彌補了現階段低應力三軸度斷裂模型缺乏微觀斷裂機理支持的局限性。但VNISFM 模型仍存在模型參數較多、校準工作量大的不足。

綜上所述，國內外學者已對金屬材料的斷裂預測方法進行較多研究，但這些研究主要集中在材料處于單一高應力三軸度或低應力三軸度應力狀態下，對復雜應力狀態下的鋼材斷裂性能研究尚不充分。本文采用理論模型、有限元分析和斷裂試驗相結合的方式，對文獻[8]的鋼材韌性斷裂模型進行了改進。采用Fortran 語言將斷裂模型編寫USDFLD 子程序，將其植入有限元程序ABAQUS，預測了十字型節點試件在復雜應力狀態下的斷裂破壞過程，驗證了本文斷裂模型的正確性。

1 應力狀態表征

在復雜應力狀態下，鋼材的韌性可由材料斷裂前承受的等效塑性應變(下文稱為斷裂應變)衡量。鋼材在斷裂前可承受的等效塑性應變越大，鋼材的韌性越好，抵抗斷裂的性能越強[17-18]。

為定量考察應力狀態對鋼材斷裂應變的影響，需要引入應力空間概念。對于各向同性材料中任意一點P，引入主應力坐標系(σ1，σ2，σ3)，如圖3 所示。直線OZ為靜水軸，過原點且與靜水軸垂直的平面為π 平面。θ 稱為羅德角[19]，標志P點在π 平面上的投影位置(0≤θ≤π/3)。

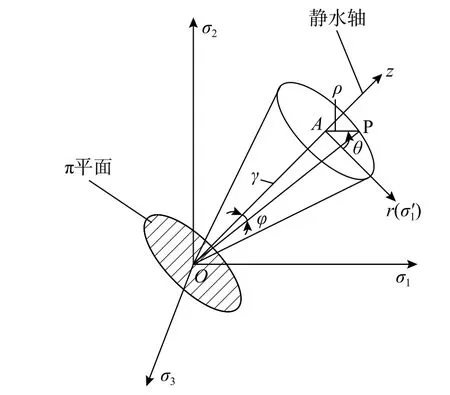
圖 3 材料點的應力狀態Fig. 3 Stress state of material point

以O為原點，以靜水軸為z軸，建立柱坐標系，主應力狀態OP可由一組柱坐標(γ，ρ，θ)表示。由于γ、ρ 的值會隨坐標軸位置的改變而變化，在韌性斷裂研究中為便于建立塑性本構關系，通常采用等價坐標不變量(I1，J2，θ)表征一點的應力狀態。其中，I1為應力張量的第一不變量，J2為應力偏張量的第二不變量。

等效應力σeq是三維應力狀態向一維應力狀態的一種數值等效，對鋼材通常可取為von Mises 應力，如式(1)；應力三軸度T定義為靜水應力與等效應力之比，如式(2)；羅德參數L定義為第二主應力位于第一、三主應力之間的相對位置關系，與羅德角θ 呈正相關，如式(3)。

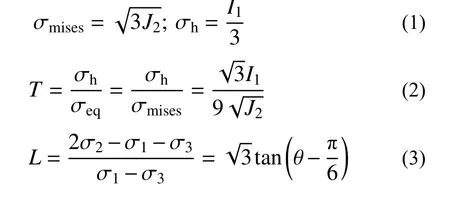
2 韌性斷裂模型的構建

2.1 體胞分析方法

鋼材是一種宏觀連續材料，可近似看作是由大量完全相同的代表性體積元(體胞)緊密堆積在一起構成。為研究這種材料變形、損傷和斷裂的力學行為，可通過對簡單的體胞模型進行分析[3]，從而將細觀尺度上體胞基體材料與空穴共同作用得到的力學響應轉化為宏觀尺度上材料的整體材性。體胞模型的選取取決于空穴空間排列假定，其中最常用的假定為立方體胞模型。如圖4 所示，鋼材可看作是由圖中完全相同的立方體胞堆積構成，且立方體胞中心含有一個球形空穴。

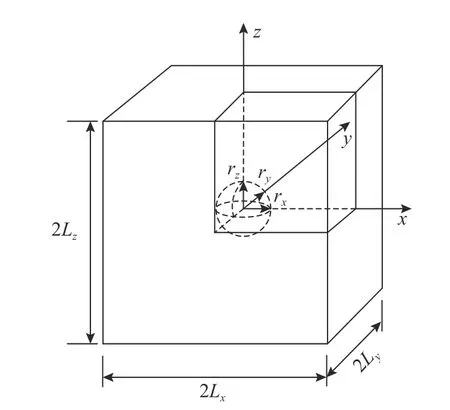
圖 4 立方體胞模型Fig. 4 Cube cell model

體胞模型分析重點在于計算空穴體積百分比fvoid、等效應力σeq及宏觀等效應變εeq。立方體胞模型中心含有單個形狀為球體的空穴，根據其三重對稱性，取體胞的1/8 進行有限元分析，建立主方向為(x，y，z)的直角坐標系，如圖4 所示。

在ABAQUS 軟件中建立立方體晶格體胞模型，如圖5 所示，模型單元采用三維實體單元(C3D8R)。體胞的基體材料選用典型的Q345 材料，冪強化系數n=0.22，彈性模量和泊松比分別為E=205 000 MPa 和ν=0.3。體胞模型基于空穴的空間周期性分布而建立，在任意變形歷程中三個外表面均需保持平面且平行于初始外表面，如圖6 所示。

對立方體胞模型進行加載時，需要使體胞的應力三軸度T和羅德參數L在變形過程中保持為恒定常數，因此本文采用基于弧長法的ABAQUS/Riks 分析步進行加載。荷載以表面壓強的形式分別施加于三個外表面，從而達到應力三軸度T和羅德參數L在變形過程中保持不變的目的。

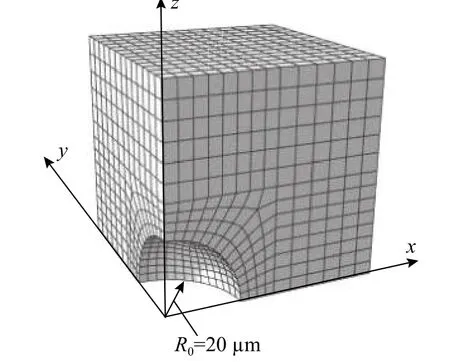
圖 5 立方體胞有限元模型Fig. 5 Cube Cell Finite Element Model

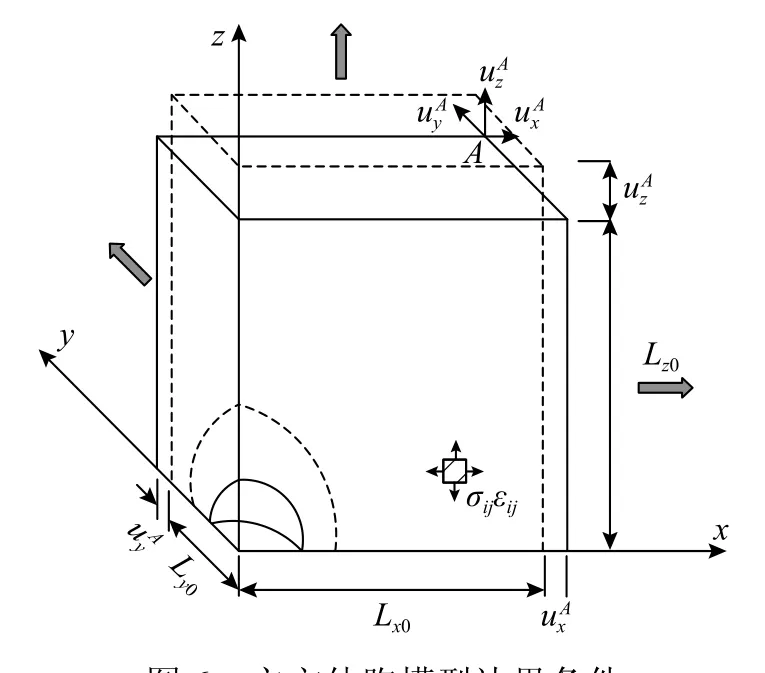
圖 6 立方體胞模型邊界條件Fig. 6 Cube cell model boundary conditions

2.2 體胞分析結果

2.2.1 高應力三軸度

對于高應力三軸度區(T≥0.5)，選取應力三軸度T在[0.6，3.0]、羅德參數L在[-1.0，1.0]范圍內，共15 組不同的應力狀態進行體胞模型分析。

以應力狀態(T=2.0、L=-1)為例，圖7 顯示了體胞模型隨塑性應變發展的演化過程。從圖中可以看出，空穴隨著塑性應變的發展逐漸長大，當塑性應變εeq達到0.3 時，相鄰空穴間幾乎已無基體材料，此時體胞失效。因此，高應力三軸度下體胞失效機理為相鄰空穴貫通。

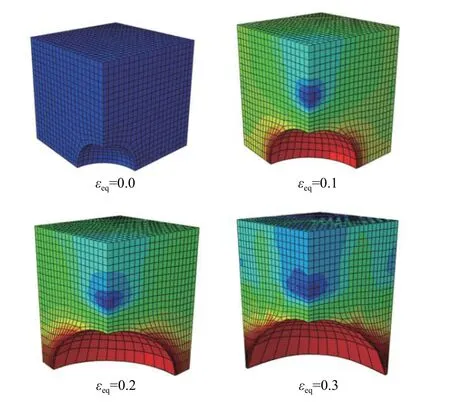
圖 7 體胞模型隨塑性應變發展演化過程(T=2.0、L=-1)Fig. 7 Somatic cell model evolution process (T=2.0, L=-1)

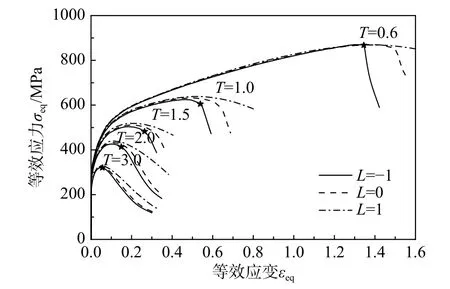
圖 8 等效應力-應變關系Fig. 8 Equivalent stress-strain relationship

圖8 顯示了體胞等效應力-等效應變關系曲線，圖中等效應力下降的拐點可看作體胞失效的臨界點[20]。從圖中可以看出：1)隨著應力三軸度T增大，應力三軸度T相同的3 條曲線越來越接近，表示羅德參數L的影響越小；2)以L=-1 為例，圖中以特殊符號標出了體胞失效臨界點，臨界應變值隨著應力三軸度T的增加而減小。

2.2.2 低應力三軸度

對于低應力三軸度區(T＜0.5)，選取應力三軸度T范圍為[-0.2，0.4]，變化間隔為0.1，羅德參數L范圍為[-1.0，1.0]，變化間隔為0.25，共63 組不同的應力狀態進行體胞模型分析。

以應力狀態(T=0、L=0)為例，圖9 顯示了體胞模型隨塑性應變發展εeq的演化過程。如圖9 所示，空穴隨著塑性應變發展而逐漸變小直至閉合，體胞失效機理為空穴閉合促使塑性剪切帶形成[21]。

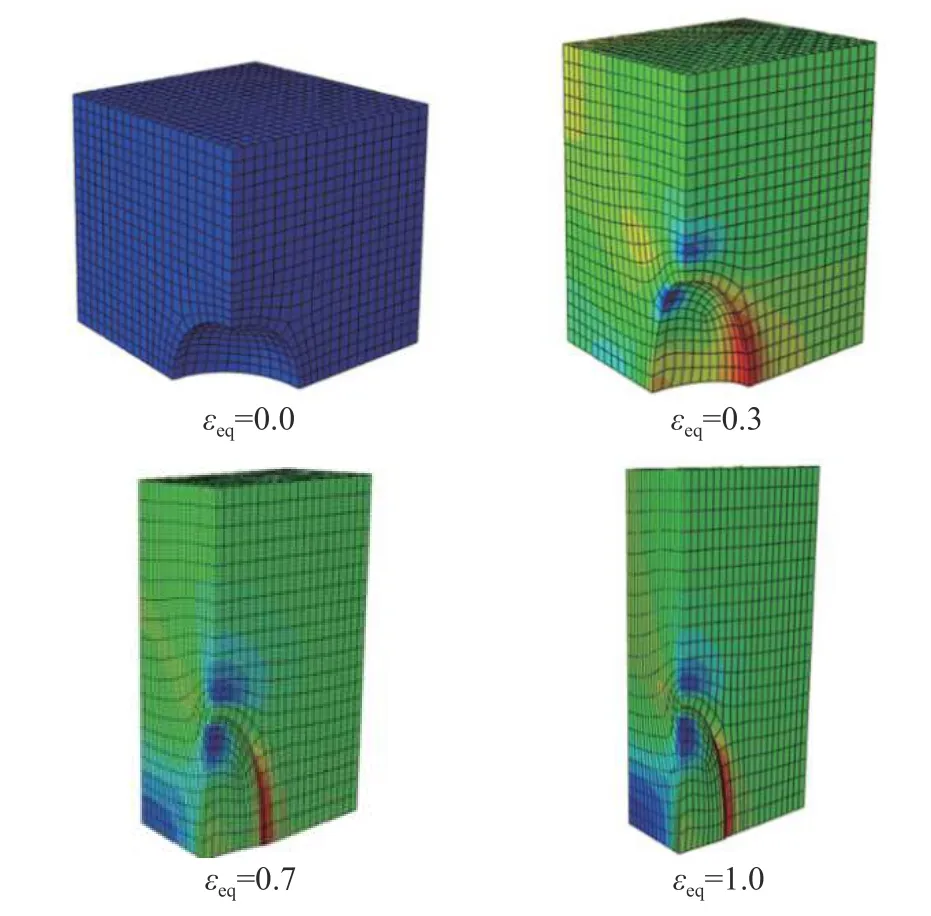
圖 9 體胞模型隨塑性應變發展演化過程(T=0、L=0)Fig. 9 Somatic cell model evolution process (T=0, L=0)

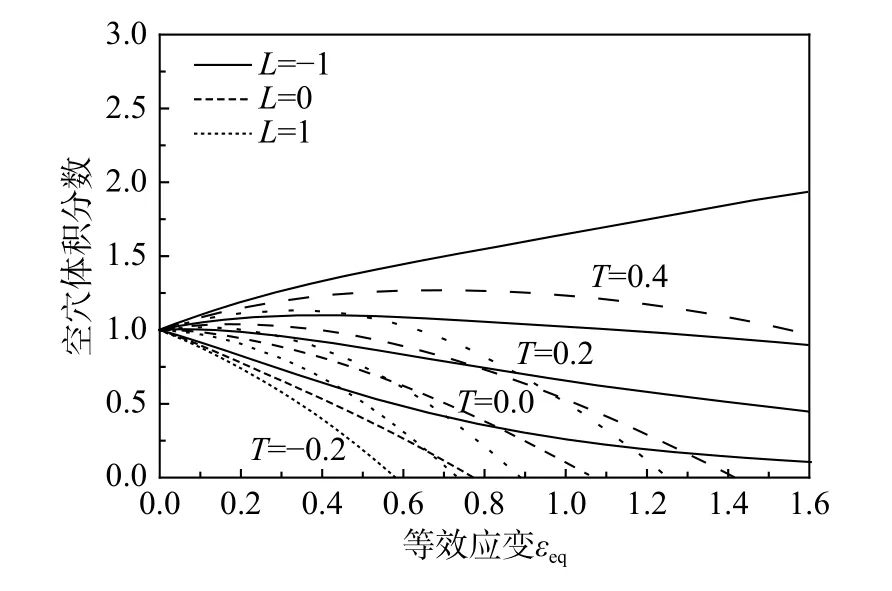
圖 10 低應力三軸度空穴體積分數演化Fig. 10 Evolution of volume fraction of low stress triaxiality void

圖10 給出了其中12 組有代表性的應力狀態下的空穴體積分數演化曲線，圖中空穴體積分數降為0 的點可看作空穴閉合臨界點。從圖中可以得出以下結論：1)應力三軸度T越高，空穴閉合的臨界應變值越大，即臨界應變值與應力三軸度T呈正相關；2)羅德參數值L越小，空穴閉合的臨界應變值越大，即臨界應變值與羅德參數呈負相關。

2.3 斷裂準則推導

本文認為在微觀尺度上體胞失效時刻對應宏觀尺度上材料斷裂起始時刻。因此，根據體胞分析結果得到體胞失效臨界應變εcr與應力三軸度T和羅德參數L的關系式，再將其轉化為宏觀尺度上的材料斷裂應變表達式即得到材料韌性斷裂準則。

2.3.1 高應力三軸度

圖11 顯示了15 組不同應力狀態下體胞失效的εcr-T數據點，在同一個應力三軸度T下，當羅德參數L分別為(-1，0，1)時，相同的應力三軸度T對應的臨界應變值幾乎重合。因此，在高應力三軸度下，羅德參數的影響很小，可近似忽略。

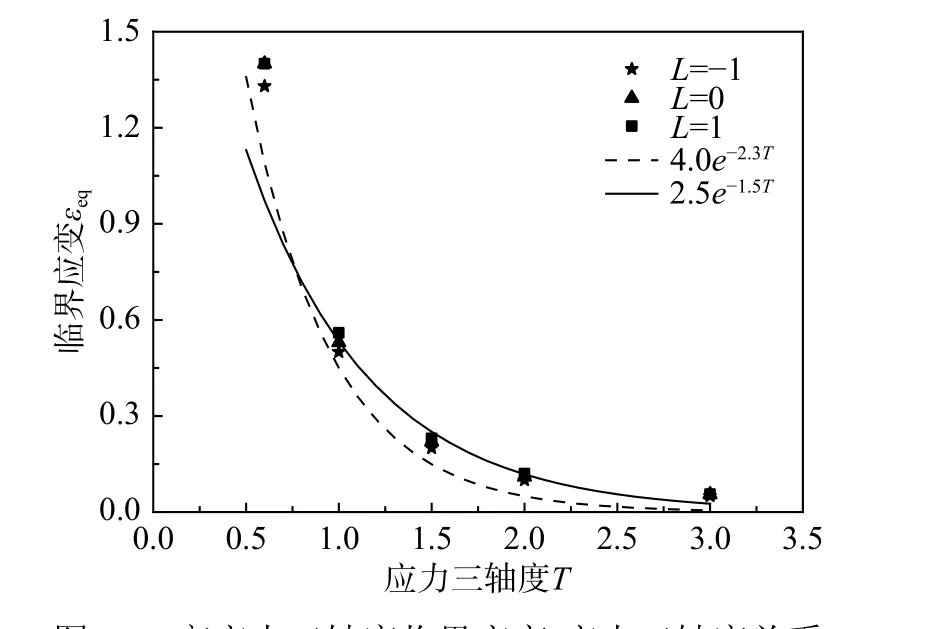
圖 11 高應力三軸度臨界應變-應力三軸度關系Fig. 11 The relationship of critical strain-stress triaxiality in high stress triaxiality area

2.3.2 低應力三軸度

1) 剪切斷裂準則構建

基于低應力三軸度區體胞分析結果，本文參照Rice-Tracey 模型的冪指數形式，分別構造臨界應變εcr與應力三軸度T的關系式以及臨界應變εcr與羅德參數L的關系式：

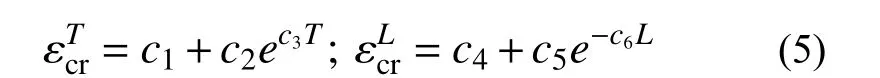
基于式(5)的形式，構造式(6)表示低應力三軸度體胞失效臨界應變εcr與應力三軸度T和羅德參數L的相關性：

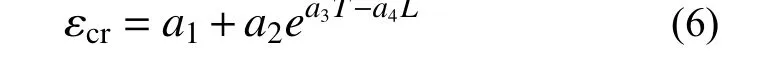
式中，a1、a2、a3、a4為自由參數。

圖12 顯示了63 組不同應力狀態下體胞失效的εcr-T-L數據點，采用式(6)對圖中的數據點進行擬合，得到a1=0.55，a2=0.51，a3=2.44，a4=1.43。

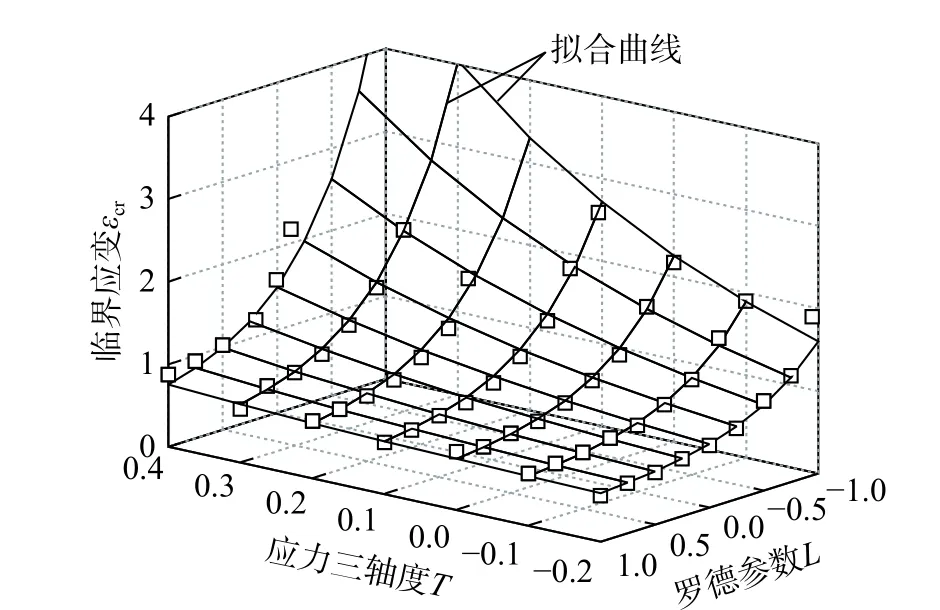
圖 12 低應力三軸度臨界應變-應力三軸度-羅德參數關系Fig. 12 The relationship of critical strain-stress triaxiality-Rod parameter in low stress triaxiality area

式中：εnc是導致空穴形核的等效塑性應變；εcr是導致空穴坍塌和局部剪切帶形成的臨界應變；p1、p2和εc是相應的系數；T為應力三軸度；n為冪強化系數。

由式(6)和式(7)得到空間應力狀態下的剪切斷裂應變計算公式(8)：

2) 剪切斷裂公式簡化

式(9)中含有4 個自由參數，校核工作量大，不利于工程實際應用。因此，根據現有的研究結果和數學方法[8,22-23]對式(9)進行簡化，減少自由參數數量。

此外，應力三軸度T與羅德參數L有對應關系式(12)[8,22-23]，對L分別取T的一階導數與二階導數，并令T=0，有式(13)。

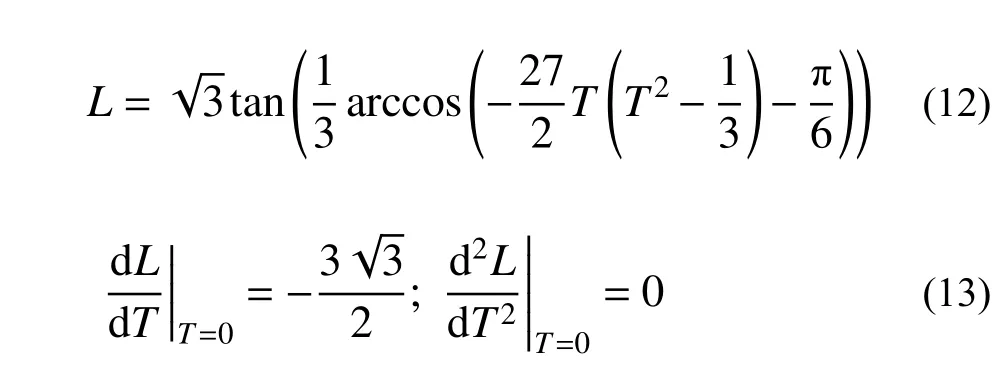
由式(13)、式(10)和式(11)有：

式(15)中參數(q3T-q4L)反映空穴演化的微觀結構特征，其中羅德參數L的自由參數q4表示對空穴形狀的影響程度。研究發現[22]，實際金屬材料中空穴形狀對材料性能的影響較小，可對自由參數q4進行簡化處理。由于斷裂應變對q4與冪強化參數n皆呈正相關[21]，故將q4近似地取為冪強化系數n。因此，式(15)可簡化為式(16)：

綜上所述，低應力三軸度區空間應力狀態下的剪切斷裂準則經簡化后寫成式(16)。

2.3.3 復雜應力狀態

通過區分拉伸斷裂模式和剪切斷裂模式，聯合式(4)和式(16)，以最低斷裂應變作為極限斷裂應變(εf)得到整體斷裂準則，如式(17)。根據Bao 等[6]的研究結論，T≤-1/3 時鋼材不會發生斷裂，故本文斷裂模型的極限斷裂應變計算公式適用于T＞-1/3。

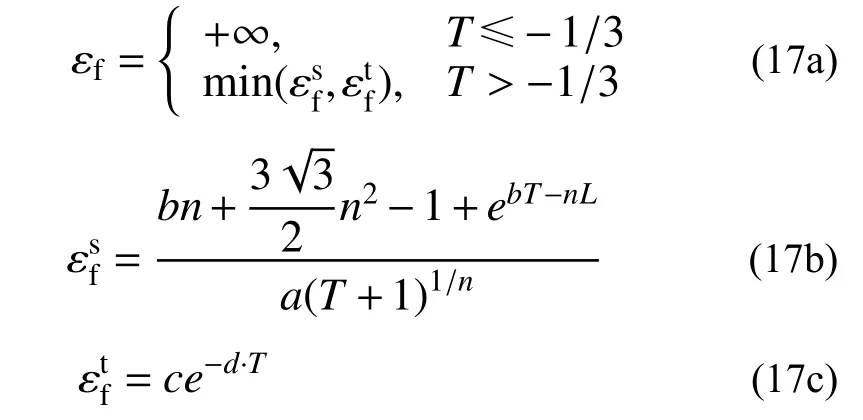
由于韌性斷裂模型(式(17))描述的是材料在加載過程中應力狀態基本保持不變時的斷裂應變，故不能直接用于實際工程問題的計算。為定量描述材料損傷的累積過程，還需引入與塑性應變增量相關的損傷因子增量(ΔD)對韌性斷裂模型進行調整，以考慮每個增量中的當前應力狀態。

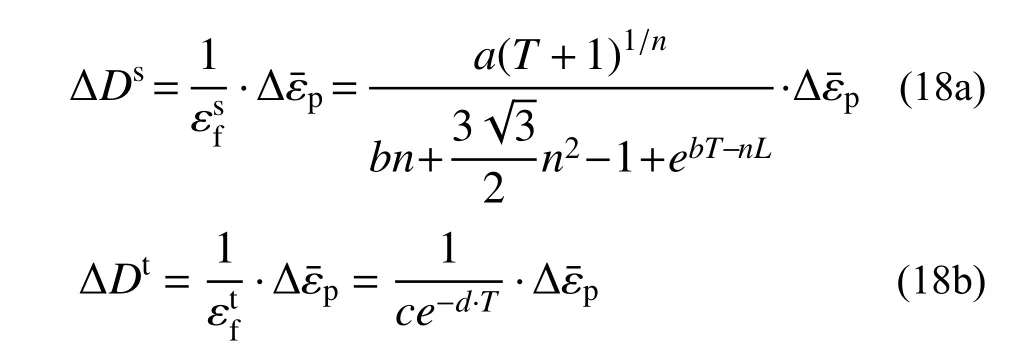
式中，ΔDs和ΔDt分別是由剪切荷載和拉伸載荷引起的損傷增量。

根據線性累計損傷理論[24]，累積每一加載步產生的損傷因子增量，定義總損傷因子D達到1 時材料產生破壞，故聯合式(18)即可得到韌性斷裂損傷模型：

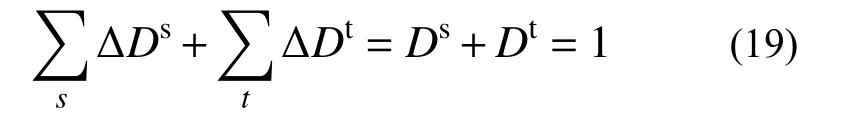
3 模型參數校核

本文基于文獻[8, 22]完成的開槽圓棒試樣NRB10、開槽平板試樣GPS2 和剪切平板試樣S0的單軸拉伸試驗結果，通過ABAQUS 有限元模擬方法獲得試件斷裂起始位置的應力狀態，在此基礎對本文韌性斷裂模型參數進行校核。

3.1 試驗介紹[8,22]

NRB10 試 樣、GPS2 試 樣 及S0 試 樣 均 由1200 mm 長、440 mm 寬和20 mm 厚的Q345 鋼塊切割而成，設計尺寸見圖13。其中NRB10 試樣和GPS2 試樣為高應力三軸度區拉伸試件，S0 試樣為低應力三軸度區剪切試樣。試驗采用MTS-810 材料試驗系統，引伸計標距為50 mm，延伸率為30%。

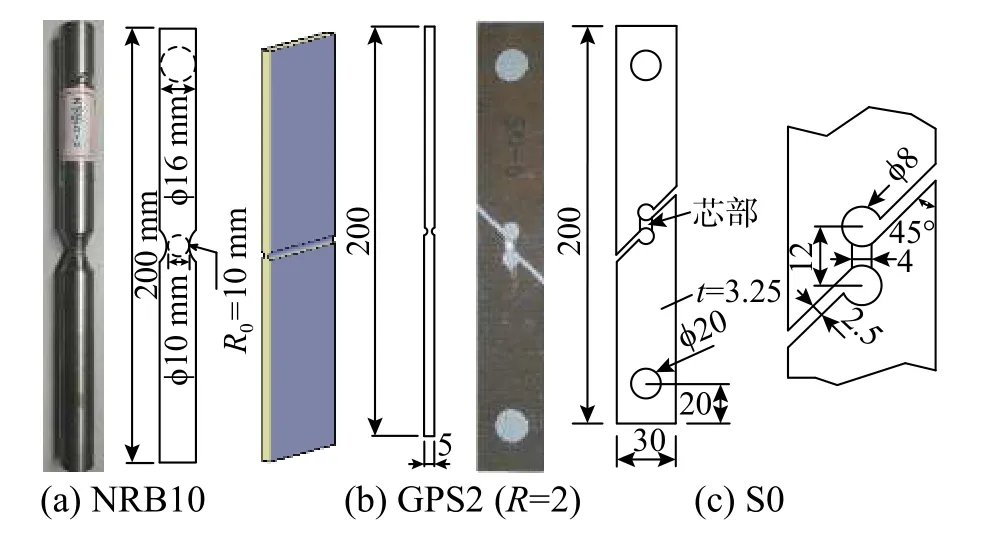
圖 13 Q345 試樣設計尺寸 /mmFig. 13 Q345 sample design size

3.2 數值模擬

對NRB10 試樣、GPS2 試樣及S0 試樣分別進行數值模擬分析，以獲得試樣斷裂起始位置的斷裂應變和應力狀態。在ABAQUS 軟件中分別建立NRB10 試樣軸對稱有限元模型、GPS2 試樣的1/8 模型、S0 試樣沿厚度方向的1/2 模型，3 種試樣的有限元模型及邊界條件如圖14 所示。根據文獻[8]得到的超景深三維觀測結果，Q345 鋼材材料特征長度取為250 μm，因此對NRB10 試樣、GPS2 試樣有限元模型的槽口單元及S0 試樣芯部單元分別進行加密，單元長度取為250 μm。

3.3 參數校核

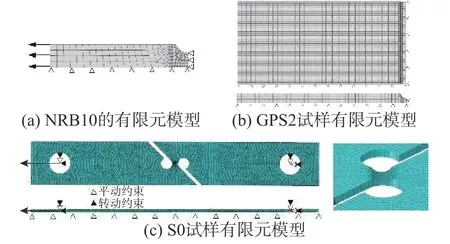
圖 14 NRB10 試樣、GPS2 試樣及S0 試樣有限元模型Fig. 14 Finite element model of NRB10, GPS2 and S0

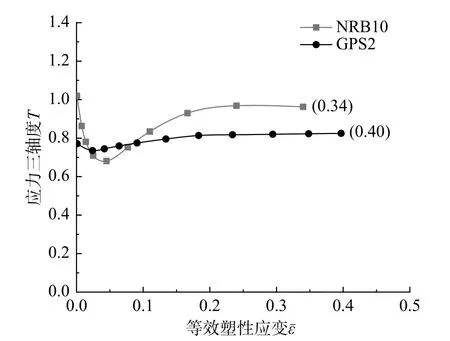
圖 15 NRB10、GPS2 試驗斷裂起始位置應力狀態Fig. 15 Stress state of NRB10 and GPS2 fracture start position

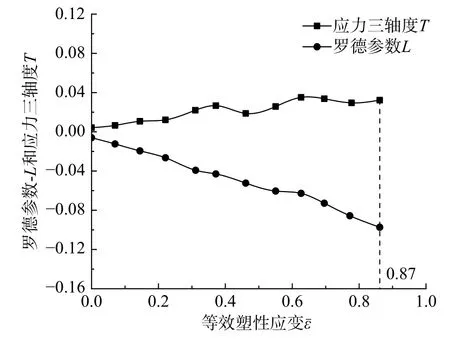
圖 16 S0 試樣斷裂起始位置的應力狀態Fig. 16 Stress state of S0 fracture start position

圖15 顯示了NRB10 試件和GPS2 試件斷裂起始位置(槽口截面中心)的應力三軸度，圖16 顯示了S0 試樣斷裂起始位置(芯部外表面中心)的應力三軸度T和羅德參數L。如圖15、圖16 所示，斷裂起始位置的應力狀態在加載過程中不恒定，因此本文取平均應力三軸度Tav和平均羅德參數Lav表征斷裂起始位置的等效應力狀態[5-6]。平均應力三軸度Tav和平均羅德參數Lav分別根據式(20)和式(21)計算。

高應力三軸度下的NRB10 試樣和GPS2 試樣的平均應力三軸度Tav分別為0.85 和0.79，斷裂應變分別為0.34 和0.40。低應力三軸度下的S0 試樣平均應力三軸度Tav和平均羅德參數Lav分別為0.02 和-0.05，斷裂應變為0.87。

將高應力三軸度下的兩組Tav-εf對應關系{Tav=0.85，εf=0.34}和{Tav=0.79，εf=0.40}代 入 式(17c)，求解一組非線性代數方程，校核得到c=2.97、d=2.55。因此，斷裂模型拉伸分支寫成式(22)。

斷裂模型剪切分支(式(17b))中含有2 個未知參數a、b，不能只由一組等效應力狀態{T=0.02，L=-0.05，εf=0.87}直接校核。研究表明[22]，當應力三軸度高于1/3 時總會發生拉伸斷裂，因此假設剪切斷裂分支和拉伸斷裂分支由軸對稱拉伸應力狀態(T=1/3，L=-1)作為分界。將T=1/3 代入式(22)得到另一組等效應力狀態{T=1/3，L=-1，εf=1.265}。將這兩組Tav-Lav-εf對應關系分別代入剪切斷裂模型(式(17b))，其中冪強化系數n=0.22[8]，求解一組非線性代數方程，得到a=1.66、b=5.37。因此，斷裂模型剪切分支寫成式(23)。

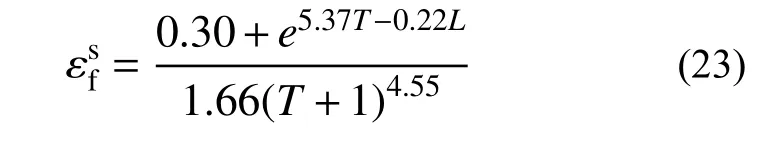
聯合斷裂模型拉伸分支和剪切分支參數校核結果，得到Q345 鋼材在復雜應力狀態下的斷裂模型如式(24)。

4 斷裂模型的應用與驗證

本文提出的韌性斷裂模型同時考慮了斷裂中拉伸與剪切組合貢獻，適用于拉-剪復雜應力狀態下的鋼節點斷裂問題分析，為評估節點的安全性提供強有力工具。

4.1 試驗介紹

本文采用十字型鋼節點試件研究拉-剪復雜應力狀態[25]，對模擬鋼結構梁柱節點的斷裂破壞行為具有一定的參考價值。本文設計了如圖17 所示的Q345B 十字型鋼節點試件(C12 試件)，其由16 mm厚的Q345B 鋼板雙面打磨至12 mm 后經線切割加工而成。

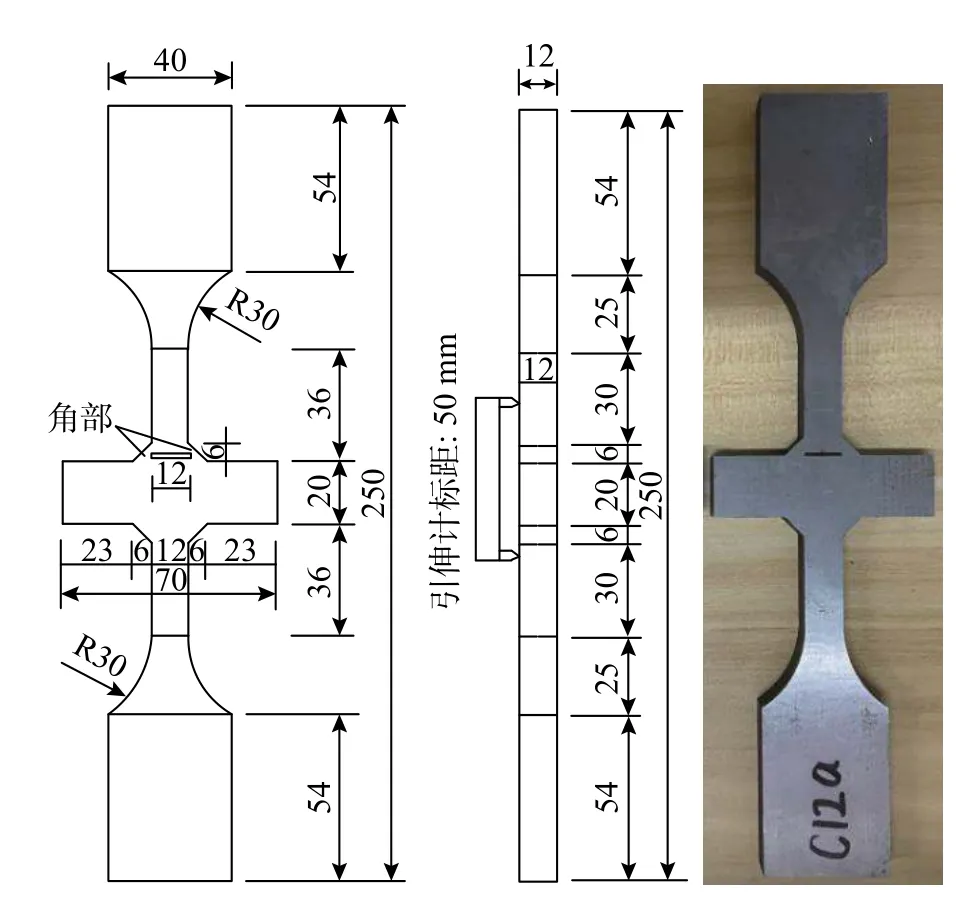
圖 17 C12 試件尺寸 /mmFig. 17 Specimen size of C12 specimen

C12 試樣中加工了一條初始間隙，該間隙用于模擬梁柱節點角焊縫焊接時未焊透而留下的間隙。間隙寬度為1 mm，長度為12 mm，間隙貫穿試件，共加工3 個相同試件。試驗采用MTS Landmark 測試系統進行拉伸試驗，通過引伸計測量50 mm 標距范圍內的變形。

圖18 顯示了C12 試件的斷裂破壞試驗現象。如圖18(a)，隨著位移加載，試件初始間隙開始變寬，同時試件角部材料發生頸縮，在初始間隙上表面兩角處開始產生裂紋；如圖18(b)，裂紋產生后向兩側角部傾斜擴展，形成大約45°的傾角直至試樣完全斷裂。

圖 18 C12 試件斷裂破壞試驗現象Fig. 18 Test phenomenon of C12 fracture and failure

4.2 斷裂過程模擬及分析

采用ABAQUS 軟件建立引伸計標距內的有限元模型，對初始縫隙兩側局部單元網格進行加密，縫隙附近加密區網格尺寸取0.25 mm，如圖19 所示。

采用Fortran 語言編寫斷裂損傷模型(式(18)和式(19))的子程序，借助用戶子程序USDFLD，將校核的斷裂模型植入到ABAQUS 中。當單元的累積損傷D達到1 時，判斷該單元失效，然后根據新的應力狀態繼續進行有限元計算，直到試樣完全破壞。同時可根據單元的失效順序預測裂紋的擴展方向。

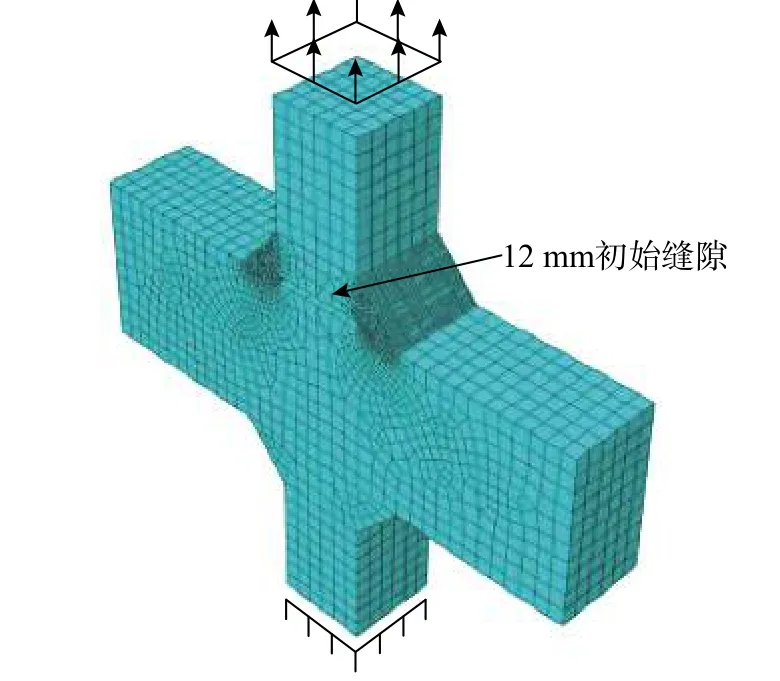
圖 19 C12 試件有限元模型Fig. 19 Finite element model of C12

將式(24)所示的斷裂模型校核結果代入子程序對C12 試件在單調加載下的斷裂破壞進行有限元計算分析，計算得到試樣的荷載-位移曲線如圖20 所示，可見有限元計算曲線與試驗曲線吻合良好，同時還發現，C12 試件的試驗曲線與模擬曲線的最后下降段曲線基本呈線性，因此將最后下降段的起點定義為斷裂點[13,16]。

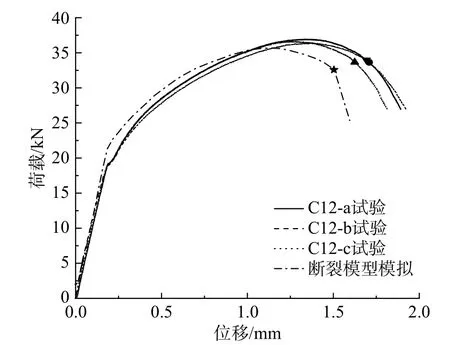
圖 20 C12 試件的荷載-位移曲線Fig. 20 Load-displacement curve of C12

基于圖20 得到的試樣斷裂荷載及斷裂位移列于表1，表1 給出了試樣斷裂荷載及斷裂位移模擬結果與試驗結果的對比情況，可見預測誤差均在15%之內，滿足工程應用精度要求。因此，本文提出的韌性斷裂模型具備良好的預測精度。

圖21 顯示了C12 試件數值模擬預測的裂縫擴展歷程，C12 試件的斷裂起始位置位于初始縫隙上表面兩角，裂紋擴展路徑與試驗觀測結果一致。因此，本文提出的韌性斷裂模型能夠準確捕捉十字型鋼節點試件的斷裂起始位置及裂縫擴展路徑，并具有良好精度。

表 1 試驗結果與斷裂模型計算結果對比Table 1 Comparison of test results with fracture model calculation results

圖 21 C12 試件模擬裂縫擴展歷程Fig. 21 Crack propagation process of C12 specimen fracture simulation

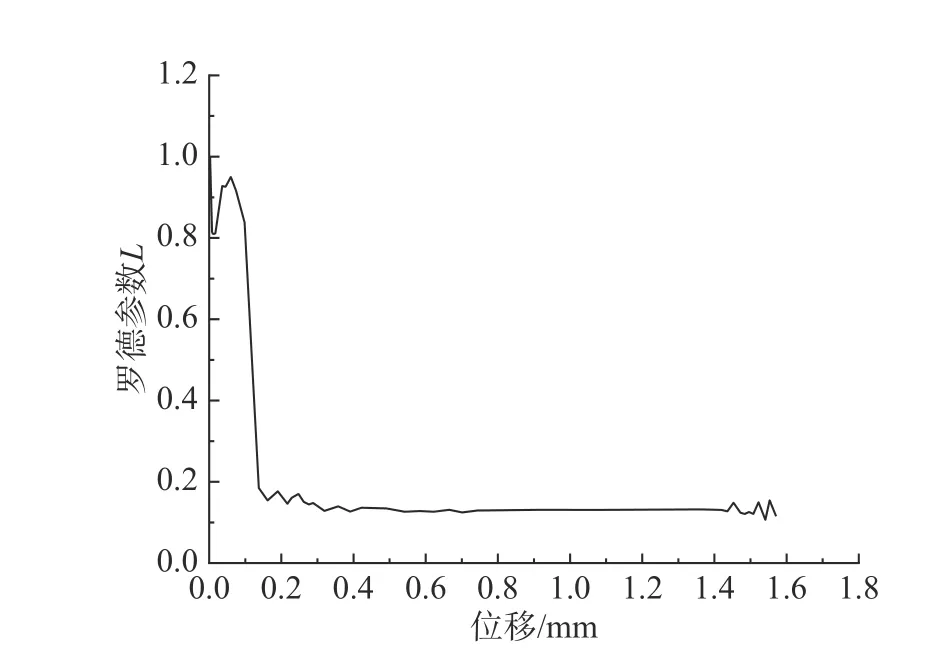
圖 23 C12 試件斷裂起始位置羅德參數變化歷程Fig. 23 Rod parameter at the fracture start position of C12

圖22 和圖23 分別顯示了C12 試件斷裂起始位置在加載過程中應力三軸度T和羅德參數L的變化歷程。從圖中可以看出，C12 試件斷裂起始位置的應力三軸度T在加載過程中處于0.5～0.8 附近波動；羅德參數L在加載過程中處于0.1～0.9 附近波動，表明C12 試件在加載過程中縫隙兩側角部處于拉-剪復雜應力狀態。因此，本文提出的同時考慮應力三軸度T和羅德參數L影響的韌性斷裂模型，對預測結構鋼材在復雜應力狀態下的斷裂行為具有良好工程應用前景。

5 結論

本文基于體胞模型空穴演化機理改進了現有的鋼材韌性斷裂模型，并校核了Q345 鋼材斷裂模型參數。以一組十字型鋼節點試件為例，驗證了改進后的韌性斷裂模型用于預測鋼節點斷裂行為的適用性和準確性。主要結論如下：

(1) 本文采用體胞分析方法研究了鋼材微觀斷裂機理，量化了空穴演化隨應力三軸度及羅德參數的變化規律。體胞分析表明：① 應力狀態對鋼材韌性斷裂性能的影響需要由應力三軸度T和羅德參數L這兩個應力參數共同表征；② 在高應力三軸度區，空穴長大至失穩的臨界應變值與應力三軸度T呈負相關，羅德參數L對臨界應變值的影響很小，可近似忽略；在低應力三軸度區，空穴閉合形成塑性剪切帶的臨界應變值與應力三軸度T呈正相關，與羅德參數L呈負相關。

(2) 本文將體胞模型隨應力三軸度T及羅德參數L的演化規律轉化為宏觀尺度上材料的整體材性，分別推導了高應力三軸度和低應力三軸度下斷裂應變關于應力三軸度T和羅德參數L的表達式。與已有鋼材韌性斷裂模型相比，簡化了斷裂模型形式和參數校核過程。

(3) 對其他學者完成的3 組不同類型的Q345鋼材材性試驗進行有限元模擬分析，根據模擬得到的斷裂起始位置的應力狀態校核了Q345 鋼材韌性斷裂模型參數。

(4) 完成了一組Q345 鋼十字型節點試件單軸拉伸試驗，并用校準的斷裂模型對其進行斷裂預測分析，模擬預測誤差小于15%且能準確捕捉鋼材斷裂起始位置及裂縫擴展路徑，在拉-剪復合型應力狀態下驗證了本文的鋼材韌性斷裂模型的適用性和準確性。