黃河源區潛在蒸散量估算方法適用性分析

李云鳳，王文科，王國慶，劉翠善，鄭昊昌，馬稚桐

（1.長安大學水利與環境學院，陜西 西安 710054；2.長安大學旱區地下水文與生態效應教育部重點實驗室，陜西 西安 710054；3.南京水利科學研究院，江蘇 南京 210029）

黃河源區是我國重要的水資源補給源頭和生態安全屏障。近年來黃河源區氣候朝著暖濕化方向發展，導致區內水熱平衡發生變化[1]。如何科學評價氣候變化對水量平衡的影響，是當前國內外研究的熱點問題，其中潛在蒸散量估算的準確性對于氣候變化下水量平衡分析和陸面水文過程模擬至關重要。

潛在蒸散發受緯度、氣候條件（水氣壓、相對濕度、溫度、風速、日照時數等）、海拔高度和地表立地條件等因素影響，其動力學過程極為復雜。迄今對于如何準確估算潛在蒸散量的問題仍然沒有得到很好的解決，對此學者提出了包括綜合法Penman-Monteith法、基于輻射的Priestly-Taylor法、Makkink法、Jensen-Haise法和Doorenbos-Pruitt法、基于溫度的Hargreaves-Samani法、Thornthwaite法、Hamon法和Blaney-Criddle法，以及基于風速的Rohwer法等在內的50余種估算方法[2]。其中Penman-Monteith法（PM法）物理意義強，綜合考慮了能量平衡和水汽擴散，計算精度高且與蒸發皿蒸發量及水面蒸發量有較高的相關性[2-3]，被聯合國糧農組織（FAO）列為計算潛在蒸散量的首選方法。但是PM法需要十分詳盡的氣象資料[4]，在氣象站點稀少的地區存在模型參數獲取困難的問題，而其他方法需要的輸入參數較少，如TH法和BC法僅需要溫度資料，在氣象資料短缺的區域，此類簡易算法的應用難度更低，可以代替PM法估算潛在蒸散量。然而不同的潛在蒸散量估算方法表現出很強的地區差異性[5]，各研究區適宜的替代模型并不相同，需要對其適用性進行評估。李晨等[6]以PM法為參考，對比了48Penman法、Hargreaves-Samani法、Pristley-Taylor法、Irmark-Allen法、Makkink法和Penman-Van Bavel法等6種簡易算法在四川省不同區域的計算精度，發現四川東部盆地區表現最好的是Hargreaves-Samani法，其他區域均為Pristley-Taylor法，48Penman法和Makkink法的偏差較大，推薦在東部盆地區使用Hargreaves-Samani法，在盆周山地區、川西南地區與川西高原區使用Pristley-Taylor法代替PM法進行潛在蒸散量的估算。劉曉英等[7]選取了華北地區6個氣象站點，探討了Priestly-Taylor法在干旱氣候條件下的適用性問題，其研究發現輻射項占比越高，Priestly-Taylor法與PM法吻合程度越高，并指出應對Piestley-Taylor法進行適當修正。隨后研究人員引入不同方法，根據區域特性校準了簡易模型的原始參數。如Bormann[8]發現不同估算方法之間存在顯著的線性關系，采用線性修正方法能夠提高替代方法與PM法的擬合程度。范文波等[9]和賈悅等[10]基于貝葉斯原理，分別在瑪納斯河流域及川中丘陵區，對Hargreaves-Samani法（即HS法）原始系數進行修正，校準后的模型平均誤差顯著降低，優化了HS法在干旱和濕潤2 種氣象條件下的應用效果。黃河源區地域遼闊，氣象站點密度相對較低，在本區及類似區域（如西藏北部高原湖盆區）應用PM法受到限制，但目前針對黃河源區潛在蒸散量簡化計算的研究尚不多見。

在此背景下，本文利用黃河源區11個站點1970—2018年逐日氣象數據，以PM法為參考，根據黃河源區氣候及下墊面特性選取6 種簡易方法（PT法、HS法、DP法、RO法、BC法和TH法）估算潛在蒸散量，對比評價各方法在黃河源區的適用性，篩選出本區適用性最強的簡易方法并根據氣象要素敏感性進行修正，以期進一步提高其在黃河源區的計算精度和適用性。研究成果對黃河源區或相同氣候條件下資料短缺的區域，選用精度高且計算簡便的潛在蒸散量估算方法有著重要的借鑒意義。

1 研究區概況

黃河源區一般指河源至唐乃亥水文站的區間[11]，位于青藏高原東緣，面積約12.2 ×104km2，源區涵蓋青海、四川和甘肅三省的16個縣級行政單元，其中設有氣象站點的縣自西向東依次為青海曲麻萊、瑪多、達日、興海、瑪沁、貴南、久治，河南蒙古自治縣，甘肅瑪曲，四川紅原和若爾蓋（圖1）。

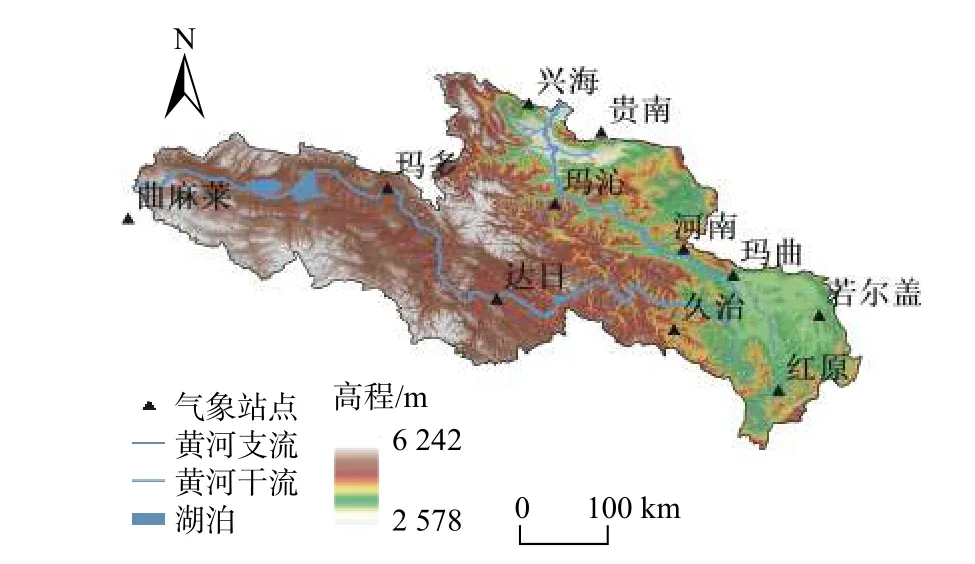
圖1 黃河源區氣象站點分布Fig.1 Spatial distribution of the meteorological stations in the headwater area of the Yellow River

黃河源區地勢較高，人類活動相對較少，區域內地貌眾多，水系發育，地下水豐富，水源涵養功能極佳。本區地勢西北高、東南低，黃河自西向東經瑪曲縣折向北方奔流，黑河、白河是其兩大主要支流及重要的水源地或產流區[1]。黃河源區80 %以上植被為高原草地、林地和沼澤[12]。氣候區劃上屬于青藏高原亞寒帶半濕潤區，平均氣溫?0.9～3.8℃。年降水量250～800 mm，自西北向東南遞增，年內變化大，降水為本區徑流的主要補給源。

2 數據來源與研究方法

2.1 數據來源

2.1.1 氣象資料

氣象數據來自中國國家氣象科學數據中心（http://data.cma.cn/），依據研究區范圍（圖1）選定11個氣象站點1970—2018年的逐日數據，數據集主要包括降水量、最低最高及平均溫度、相對濕度、風速、日照時數等。根據實測值的趨勢對數據集進行異常值修正及缺測值插補、計算潛在蒸散量并進行空間插值處理。

2.1.2 地形數據

地形數據來自中國科學院地理空間數據云（http://www.gscloud.cn/）。數據產品為SRTM3 V4.1版本，分辨率為90 m。對數據進行預處理后，重采樣為0.1°×0.1°經緯網格高程數據。

2.2 研究方法

表1列出了PM法和對比方法（DP法、PT法、BC法、TH法、HS法和RO法）的計算公式、參數物理意義、各方法優點和不足。輻射參數a=0.183，b=0.681[13]，各方法具體計算過程參見文獻[2,14]。按照Allen[15]等的研究，日尺度的土壤熱通量G相對于Rn較小，故忽略不計。對比方法選取的主要依據為黃河源區氣候條件及估算方法考慮的氣象要素。首先，針對本區輻射強烈的特性，選取了基于輻射的DP法和PT法。其次，根據本區寒冷干旱的氣候條件選取了基于溫度的BC法、TH法和HS法。最后，以考慮了風速和水汽壓的RO法作為補充。

2.3 精度評價標準

本文以PM法為參考，采用一致性系數（d）、平均偏差（MBE）、決定系數（R2）、均方根誤差（RSME）4個指標從年和月尺度上比較六種方法估算值與PM法計算結果之間的吻合程度。其中，一致性系數d及決定系數R2能夠反映被評價方法與PM法二者估計值的相關程度，指示兩者是否具有相同的變化趨勢及分布規律。平均偏差和均方根誤差能夠反映二者的偏離程度，平均偏差為正時代表正偏差，即評價方法較PM法高估了Ep，反之則為負偏差，表現為相對低估。d和R2越接近1，MBE和RSME越接近0，則該方法與PM法一致性越好，計算精度越高。各指標計算公式如下：

表1 潛在蒸發量估算公式Table 1 Estimation formula of potential evapotranspiration

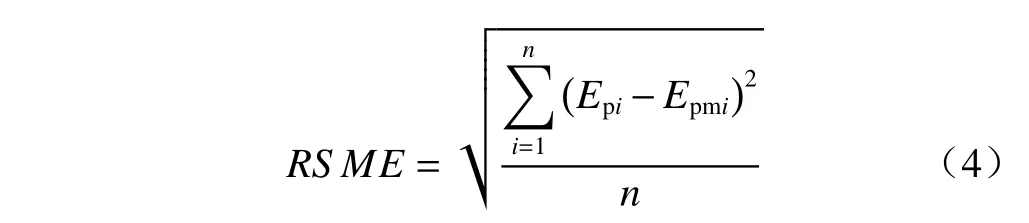
式中：n——樣本總數；

Epmi、——PM法計算值及平均值；

Epi、——六種方法計算值及平均值。

同時，為進一步分析黃河源區各簡便估算方法在空間尺度的適用性，本文對各方法計算的潛在蒸散量多年平均值進行反距離權重插值，并以PM法為標準，對比6種簡易算法與PM法二者估計值的空間分布之間的差異。

3 結果與分析

3.1 未經修正時各方法估算效果分析

3.1.1 黃河源區潛在蒸發量年值估算效果

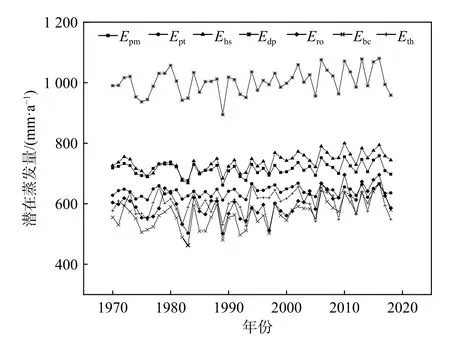
圖2 未經修正時各估算方法年潛在蒸散量時間序列Fig.2 Time series of potential evapotranspiration for each method without correction

圖2是各原始公式估算的潛在蒸散量年值序列。從圖2可以發現，7 種公式估算結果在50年間呈現微弱的上升趨勢，這是因為受局部地形的影響，各地區潛在蒸散發或表現為上升趨勢，或表現為下降趨勢[22]，導致黃河源區整體潛在蒸散發的上升趨勢并不明顯，這與劉昌明等[23]指出的1960—2007年黃河源區潛在蒸散發呈現微弱上升趨勢的結論基本一致。雖然6種方法與PM法二者估算值的年代際變化趨勢大致相同，均于80年代達到最低值，然而各方法與PM法的擬合度存在較大的差異，PM法與HS法計算的黃河源區年潛在蒸散量變化范圍為700～800 mm/a，DP法估算值在900～1100 mm/a，其余方法的計算結果在500～700 mm/a之間。HS法的年值序列與PM法最為接近，且年際波動趨勢與標準PM法基本一致，表明HS法可以較好地反映出黃河源區潛在蒸散發的年代際和年際變化，這與HS法最早在美國西部干旱地區提出[24]因而在干旱氣候下應用效果較好有關。DP法存在顯著高估的現象，這或許是原始經驗系數過大的緣故，表明未經系數修正的DP法不宜直接應用于黃河源區。RO法、BC法和TH法則存在顯著低估的現象，這是由于近年來黃河源區氣候趨于暖濕化[1]，使得僅考慮溫度的BC法和TH法變化幅度較大，同時由于黃河源區大風天數減少、風速降低，導致RO法計算的潛在蒸散量偏低。

3.1.2 黃河源區潛在蒸散量月值估算效果

從圖3可以看出，各方法估算值均在7月達到蒸發峰值，呈現出中間高兩邊低的特征。月潛在蒸散量的取值范圍在?10～150 mm/mon之間，只有BC法在1月的估算值為負值，其余方法各月的取值均為正值。從走勢上看，HS法、PT法及DP法與PM法的走勢大致相同，RO法和BC法的走勢較PM法平緩，TH法的走勢較PM法陡峭。

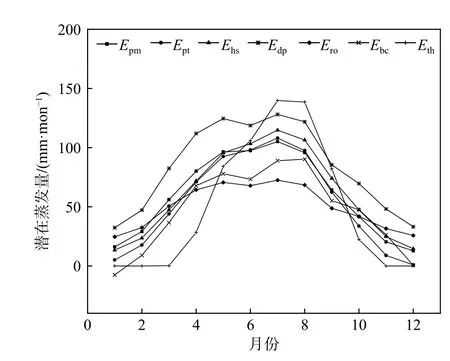
圖3 未經修正時7 種方法多年平均（1970—2018年）逐月潛在蒸散量估算值Fig.3 Uncorrected multi-year average monthly potential evapotranspiration estimation of the seven methods

各方法估算值與PM法的計算結果之間的一致性系數（d）均在0.85以上，HS法和PT法最高，達到了0.98（表2）。各方法決定系數R2在0.71～0.97之間，其中HS法、PT法和DP法3種方法的決定系數均在0.9以上，表明各方法估算值與PM法的計算結果之間的線性相關程度較高，尤其是HS法、PT法和DP法表現最優。再按平均偏差絕對值的大小對各估算方法與PM法二者的估計值之間的偏離程度進行排序，可得：HS法＜PT法＜TH法＜RO法＜BC法＜DP法。雖然HS法及PT法的均方根誤差均約為10 mm/mon，但HS法平均偏差僅為3.49 mm/mon，而PT法為?6.04 mm/mon，即HS法與PM法的吻合程度比PT法更高。未經修正時，HS法與PM法二者的估計值最為接近，在本區精度最高。結合圖3和表2可以發現，HS法僅6—9月計算的潛在蒸散量略高，且誤差較小，這是由于HS法的估算效果受區域干旱程度影響[5,24-25]，在干旱條件下精度更高。其次為PT法，月潛在蒸散量的平均偏差為?6.04 mm/mon。PT法的計算結果在輻射最強的5—9月與PM法估計值較接近，其余月份因太陽輻射較弱而遠低于PM法估計值，故整體平均偏差為負值。DP法計算的潛在蒸散量全年顯著偏高，而BC法和RO法計算的潛在蒸散量5—9月顯著偏低，這或許是由于黃河源區5—9月潛在蒸散量對相對濕度和風速的敏感性偏小，且其敏感性分別于6月和7月達到最低值[26]，使得DP法和RO法夏季誤差較大。TH法僅需要月均溫一個參數，其估算效果受氣溫影響而變化幅度較大，溫度較低時TH法計算的潛在蒸散量顯著偏低，而溫度較高時則顯著偏高。Xu等[27]研究表明TH法的應用效果亦受水分含量影響，在有充足水分供于蒸發的山谷地區最為適用。綜合圖2、圖3和表2可以看出，利用原始系數估算潛在蒸散量時，時間尺度上HS法與PM法誤差最小，適用性最強。

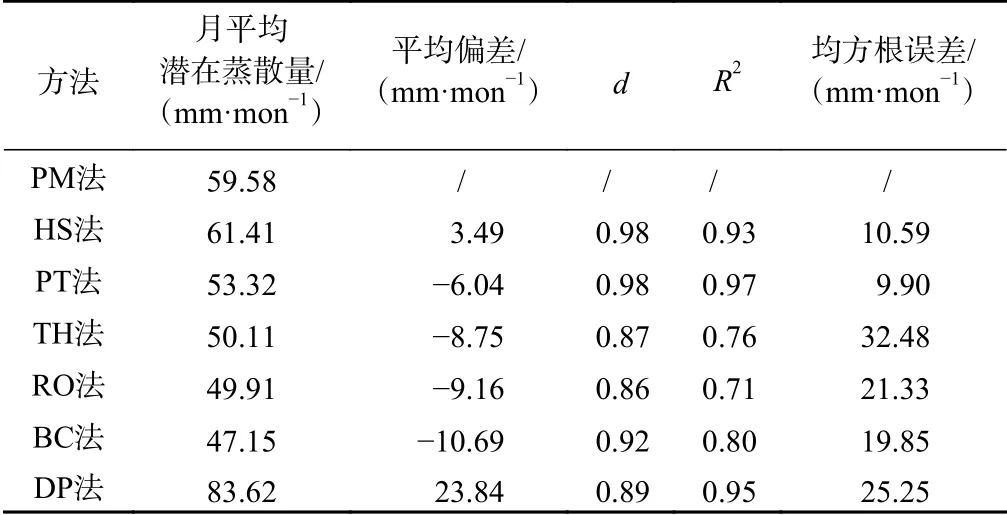
表2 未經修正時各估算方法月潛在蒸散量估算效果Table 2 Monthly potential evapotranspiration estimation effect of each estimation method without correction

3.1.3 各估算方法計算的多年平均值空間分布

為進一步分析各簡易估算方法在黃河源區空間尺度上的適用性，本文對7 種方法估算的多年平均潛在蒸散量進行空間插值，插值結果見圖4。從圖4可以看出，PM法估算的潛在蒸散量空間分布呈現由南向北遞增的趨勢，變化范圍為676.40～785 mm/a，多年平均潛在蒸散量為714.96 mm/a。其中，興海和貴南兩縣是潛在蒸散量空間分布的高值中心，為778～787 mm/a；瑪沁、達日、久治和河南等4縣為低值中心，為672 ～696 mm/a。西北部及東南部的曲麻萊和紅原等縣潛在蒸散量為708 ～735 mm/a 。

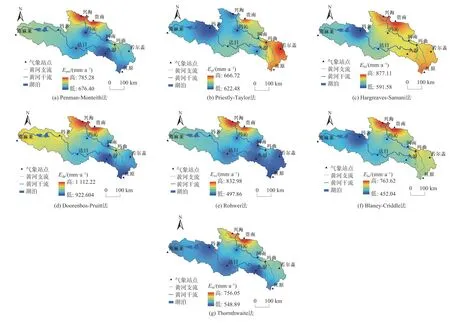
圖4 各估算方法潛在蒸散量空間分布Fig.4 Spatial distribution of potential evapotranspiration of each estimation method

對比分析6種簡易算法與PM法二者計算值的空間分布，可以發現，各簡便方法在黃河源區空間尺度上的應用效果不盡相同。除PT法外，其余方法均在空間上體現出了北部興海及貴南縣的高值中心。PT法估算的潛在蒸散量高值中心為東南部若爾蓋縣，年潛在蒸散量空間分布上呈現由東向西遞減的趨勢，在中部地區誤差較大，達98.19 mm/a。HS法估算值整體與PM法的計算結果相近，僅在東南部紅原縣、久治縣、河南縣和若爾蓋縣計算結果偏高，誤差約84.4 mm/a。DP法在整個區域計算結果偏高現象明顯，平均誤差達288 mm/a。RO法、TH法和BC法計算值明顯偏低，誤差分別為116.04，113.64，149.16 mm/a。結合各方法空間特征和黃河源區已有的潛在蒸散量與氣象因子的敏感性分析[12,28]，黃河源區各簡易估算方法計算結果的空間分布與其所含氣象因子的敏感性的空間變化基本一致，表明各簡易估算方法的適用區域與氣象因子敏感性的空間分布密切相關。綜合評價各簡易方法時間與空間尺度上的估算效果可知，HS法在本區精度最高，適用性最強，這與焦丹丹等[2]在氣候干旱的甘肅臨澤地區的研究類似。

3.2 黃河源區HS法改進后的估算效果分析

3.2.1 HS公式修正方法

為進一步提高HS法在黃河源區估算潛在蒸散量的適用性，以PM法為參考，對HS法進行改進。利用主成分分析篩選出影響潛在蒸散量估算效果的主要氣象因子，根據各氣象因子載荷值判定改進HS法需要引入的氣象因子。

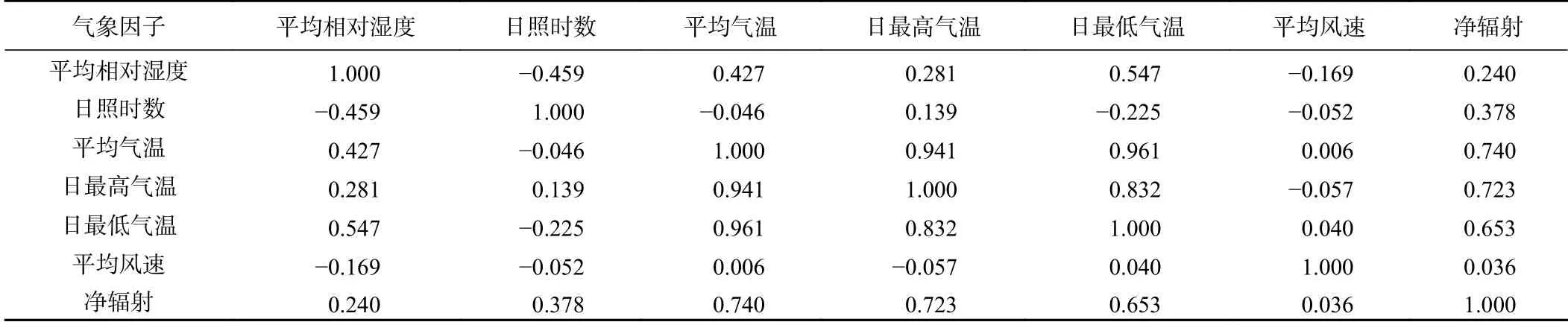
表3 相關系數矩陣Table 3 Correlation matrix

表3為HS法中所含的各氣象因子之間的相關系數，從表中可以得知：HS法所含的平均氣溫、日最高氣溫、日最低氣溫和凈輻射之間具有較高的相關系數，達到了極顯著水平。依據特征值大于1的原則，提取了前3 個主成分（表4），累積方差貢獻率達到89.505 %，表明前3 個主成分能夠解釋7 個氣象因子對潛在蒸散發的影響。表5列出了各成分的載荷值

，可以發現：第一主成分與平均相對濕度、平均氣溫、日最高氣溫、日最低氣溫和凈輻射具有較強的相關性；第二主成分與平均相對濕度和日照時數2 個氣象因子相關性較好；第三主成分只與平均風速具有顯著相關性。

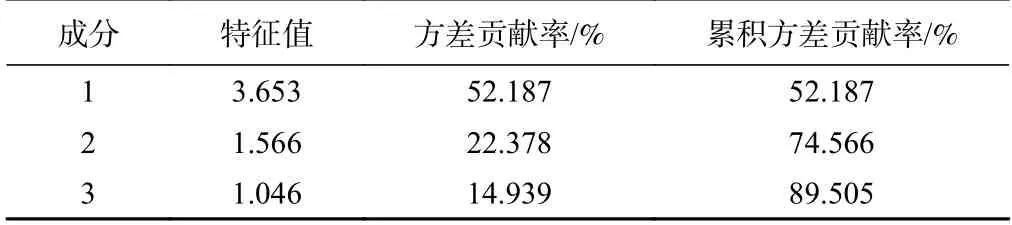
表4 總方差解釋Table 4 Explanation of total variance

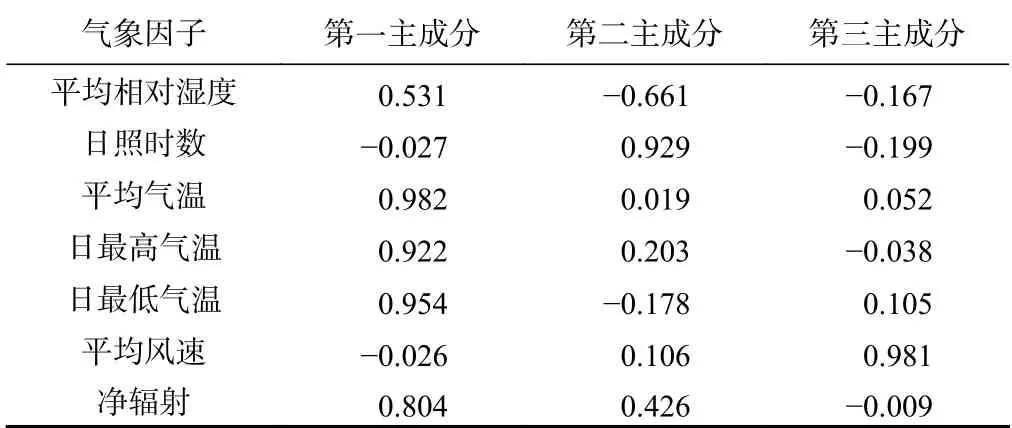
表5 初始因子載荷陣得分Table 5 Component matrix

由以上分析可知：第一、第二主成分均與平均相對濕度相關性較高，且第一第二主成分的累積方差貢獻率達74.566 %，表明平均相對濕度對于潛在蒸散發影響較大，在本區應用時應當將平均相對濕度引入HS的修正公式：

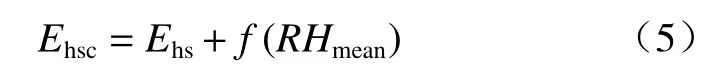
式中：Ehs——原HS公式計算的潛在蒸散量；

Ehsc——HS公式引入平均相對濕度因子后的逐日潛在蒸散量；

f(RHmean)——平均相對濕度函數。

以PM法和改進前的HS法計算所得的潛在蒸散量之差（Epm?Ehs）為因變量y，RHmean為自變量x，進行回歸分析，得到非線性回歸趨勢方程為：

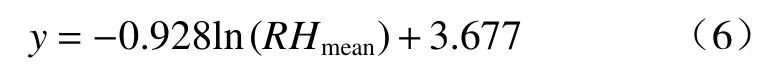
即非線性回歸方程系數a=0.928，b=3.677。通過引入平均相對濕度因子建立的HS修正公式為：

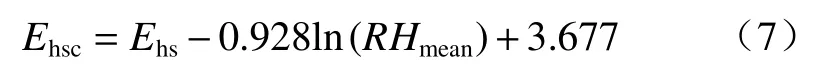
3.2.2 改進后的HS法時空尺度的修正結果分析

為分析改進后的HS法在黃河源區的應用效果，分別對改進后的HS法時間（年、月）及空間尺度上的適用性進行評估（表6）。PM法計算的多年潛在蒸散量平均值為714.96 mm/a，原HS法為736.97 mm/a，誤差為22.01 mm/a，改進后的HS法多年平均值為708.79 mm/a，誤差為?6.17 mm/a，多年月平均值與PM法的誤差也從1.83 mm/mon降到0.51 mm/mon，意味著改進后的HS法的計算精度優于未經修正的HS法。

表6 改進后的HS法計算潛在蒸散量在時間尺度的估算效果Table 6 Estimation effect of the potential evapotranspiration calculated by the improved HS method on the time scale

圖5為改進HS法與PM法的月潛在蒸散量擬合效果，改進后的HS法月潛在蒸散量與PM法擬合良好。一年中有7個月份計算值大致相等，其余月份也較為接近潛在蒸散量，最大的差值出現在4月，僅為7.39 mm/mon。

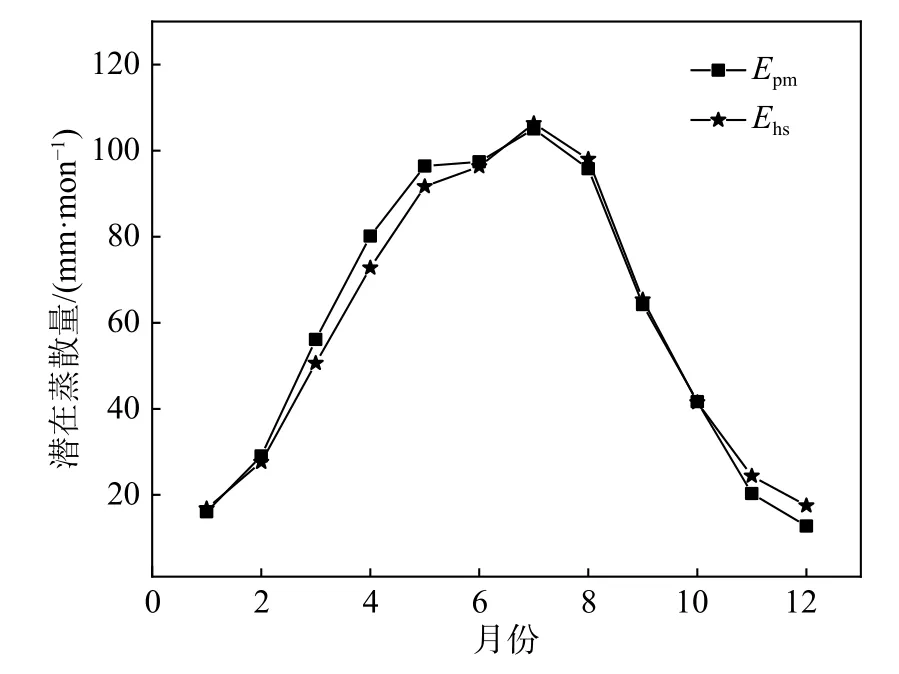
圖5 改進HS法與PM法的月潛在蒸散量擬合效果Fig.5 The fitting effect of monthly potential evapotranspiration between the improved of HS method and PM method

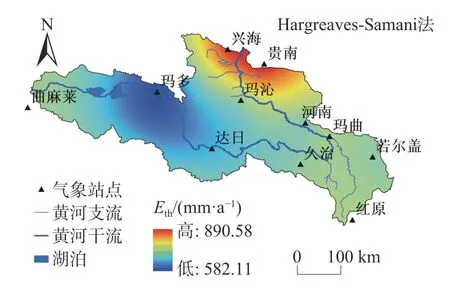
圖6 改進后的HS法多年平均潛在蒸散量空間分布Fig.6 The spatial distribution of the multi-year average potential evapotranspiration of the improved HS method

圖6為改進后的HS法潛在蒸散量多年平均值的空間分布，對比圖4與圖6，可以發現，改進后的HS法的估算值與PM法的空間分布更為接近。潛在蒸散量高值中心貴南縣為890.58 mm/a，低值中心瑪多縣為582.11 mm/a，空間分布上呈現由北向南逐漸降低的趨勢，與PM法空間分布趨勢相同。東南部紅原縣、河南縣、久治縣和若爾蓋縣，平均誤差由84.4 mm/a 降至20.42 mm/a。表明引入平均相對濕度因子后，HS法描述氣候相對濕潤的黃河源區東南部潛在蒸散量的能力得以提升。

表7為HS法改進前后的平均偏差變化情況。HS法改進后，其平均偏差有著顯著的降低，黃河源區整體的平均偏差由3.49 mm/mon降至1.03 mm/mon，與PM法偏離程度變小。在相對濕度大的河南、紅原、久治、若爾蓋和瑪曲等5縣，改進后的HS公式平均偏差顯著降低，平均降幅為5.33 mm/mon,尤以氣候最為濕潤的紅原縣修正效果為優，平均偏差降輻最大，達7.38 mm/mon。相對濕度較小的中部和西北部，除瑪沁縣和曲麻萊縣的平均偏差降低之外，其余地區的MBE表現出1～3 mm/mon的上升，意味著HS法的修正效果與相對濕度有一定聯系。

表7 HS法改進前后月潛在蒸散量平均偏差空間分布Table 7 The spatial distribution of the average error of monthly potential evapotranspiration before and after HS method improvement

綜合分析HS法改進前后在黃河源區時間及空間尺度上的應用效果，可以看出，引入平均相對濕度因子改進HS法，能夠有效解決HS法在黃河源區東南部紅原縣、河南縣、瑪曲縣、久治縣和若爾蓋縣精度不高的問題。而且，隨著近年來黃河源區日趨暖濕化，在未來氣候條件下改進后的HS法將極大地提升潛在蒸散量的估算精度，在本區有著較好的應用前景。

4 結論

（1）通過計算，黃河源區多年平均潛在蒸散量為714.96 mm/a，年內蒸散能力最大的月份出現在7月，為105.03 mm/mon。空間分布呈現由北向南逐漸降低的趨勢，蒸散能力的高值中心為北部的貴南縣，年潛在蒸散量達785.28 mm/a。

（2）6 種估算方法中，HS法無論是時間還是空間尺度，均與PM法的差值最小。其年、月值的時間序列最為接近PM法，在黃河源區的適用性最強。但仍存在紅原縣、河南縣、若爾蓋縣、瑪曲縣及久治縣精度不高的問題，需要根據區域特性進行修正。

（3）通過主成分分析，發現由于黃河源區東南部氣候濕潤，原HS公式未考慮平均相對濕度對潛在蒸散量估算效果的影響，導致HS法在東南部紅原等縣誤差較大。針對此問題，本文在HS公式中引入平均相對濕度因子，將HS公式修正為Ehsc=Ehs?0.928ln(RHmean)+3.677。HS法改進之后，黃河源區整體的年潛在蒸散量的平均偏差由?22.008 mm/a降至6.174 mm/a；月潛在蒸散量的平均偏差由3.487 mm/mon降至1.031 mm/mon；空間尺度上，黃河源區東南部的紅原縣、河南縣、若爾蓋縣、瑪曲縣及久治縣的潛在蒸散量的平均偏差明顯降低。表明HS法改進后，在黃河源區的計算精度和適用性得到進一步提升。