基于數值計算的測斜儀監測誤差分析

趙振宇

（貴州省交通規劃勘察設計研究院股份有限公司，貴州 貴陽 550038）

邊坡位移監測是判斷邊坡穩定性的重要方法。近年來，測斜儀在邊坡深部位移監測中得到廣泛應用[1-5]。馬水山等[1]通過對國內幾個典型滑坡體深部變形監測實例的分析，認為鉆孔測斜儀具有精度高、量程較大、性能可靠等特點；陳開圣等[3]將測斜儀應用到滑坡變形監測中，并與鉆探結果進行對比，對滑動面的分布情況、滑動機制作出判斷，說明測斜儀在滑坡監測中的應用是可行的；彭紀超等[4]利用RQBF-698B型鉆孔測斜儀對貴州省化樂煤礦三井區的滑坡帶進行監測，總結出一種提高鉆孔測斜儀監測效率的方法；黃飛瀾等[5]的研究表明測斜儀可檢測地基不同深度處的側向水平位移，較好地反映了地基土體內可能存在的滑裂面的位置和滑動方向。

測斜儀在邊坡變形監測中會存在一定誤差，使得監測結果偏離真實值，當誤差過大則會使技術人員對邊坡的變形做出誤判。針對測斜儀誤差的研究已有很多[6-12]，如：方大勇[6]針對邊坡長期監測中出現的部分測斜數據離散性較大、位移方向不合理的問題，提出探頭角度定位旋轉誤差是造成現場測量結果誤差的主要原因；李國維等[7]基于測斜儀工作原理，分析了滑動式測斜儀在使用過程中的誤差成因，針對測斜儀零點數據漂移問題，分別從零點漂移量恒定和零點漂移量變化兩種情況導出了對應的修正公式，基于統一基準線修正法（UBM），專門針對深孔測斜情況，應用標量和代替矢量和（以曲代直）簡化思想解決了零點漂移問題；喬美英等[10]基于遞推最小二乘的誤差補償數學模型，采用橢球擬合法、點積不變法和旋轉平面擬合法的聯合校正方法對隨鉆測斜儀進行誤差補償校正，并對隨鉆測斜儀進行數值仿真和雙軸轉臺實驗，用聯合校正方法對實驗數據進行誤差補償校正，校正后測量精度滿足隨鉆測斜儀要求；徐想[11]在三維正交傳感器基礎上推導傾斜角及方位角數學模型和計算公式，然后從理論上構建重力加速度計靜態的數學模型以及加速度計存在安裝誤差時的數學模型，利用ADAMS動力學仿真軟件構建了重力加速度傳感器精確安裝和存在安裝誤差時測量系統的物理模型。

以上針對測斜儀誤差所作的研究大多是針對監測儀器本身的誤差、環境引起的誤差和人為誤差進行的，也有學者研究了監測曲線所產生的誤差問題。就測量原理來說，測斜儀對深部水平位移的測量是根據一些有限的監測點的角度變化來計算變形曲線的水平位移值，這種以點代線的測量方法本身就存在誤差。因此本文嘗試從測斜儀測量原理和數值分析角度分析測斜儀測量誤差產生的原因。

1 深部測斜儀原理

深部位移測斜儀監測原理為：根據儀器中鉛錘受重力影響，其方向為垂直狀，測量出測試管軸線與垂直方向的夾角，計算出鉆孔內各個測點的水平位移。其基本原理如圖1所示。

圖1 測斜儀監測原理示意圖Fig.1 Schematic diagram of the inclinometer monitoring principle

在實際監測中，一般先要在邊坡鉆孔埋設測斜管，利用測斜管中內徑兩組互成90°的導向槽，將測斜儀順導向槽放入測斜管內，逐段（人工監測時標準長度為50 cm，也可自行確定）測量。當邊坡由于滑動產生傾斜變形時，通過安裝在測斜儀內的傳感器測出該段的角度變化量，利用該段長度和角度變化量計算出該段的水平變形值。對每段水平變形值進行計算并累加，即可獲得鉆孔內全長范圍的水平位移值。其計算方法為：

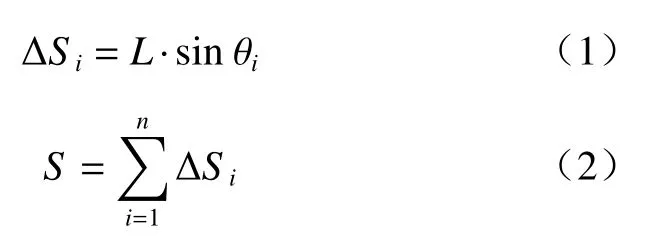
式中：L——測量段標準長度/m；

ΔSi——第i段水平位移變形值/m；

θi——第i測量段傾角/(?)；

S——水平變形總位移值/m。

2 深部測斜儀測量原理數值分析

深部位移測斜原理是利用測量孔內各段測點夾角的變化，從而計算水平位移，其數學計算方法等同于常微分方程數值解中的Euler法。Euler法解常微分方程的解法為：

有一常微分方程：

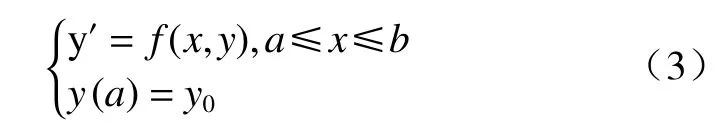
當f(x,y)對y滿足Lipschitz條件，求解式（3）一種最簡單的方法為將節點xn的導數y′(xn)用差商代替，由此式（3）可近似寫為：

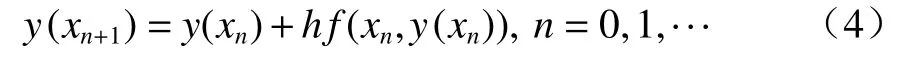
從x0開始計算y(a)=y(x0)=y0，由式(4)可得y(x1)≈y0+hf(x0,y0)=y1，再將y1≈y(x1)代入式（4）右端，得到y(x2)近似為y2=y1+hf(x1,y1)，一般寫成：

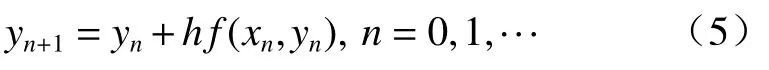
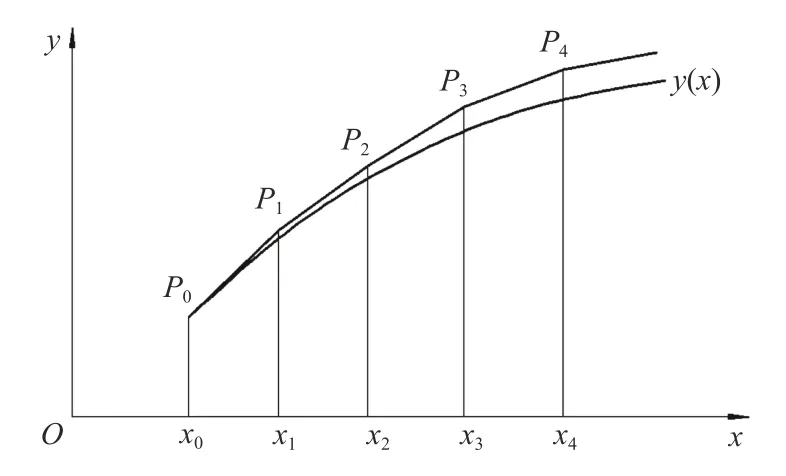
圖2 Euler法的幾何意義示意圖Fig.2 Schematic diagram of the geometric meaning of the Euler method

Euler法的幾何意義如圖2所示。式（3）的解曲線y=y（x）是從點P0（x0,y0）出發，以f(x0,y0)為斜率作一段直線，與直線x=x1交點于P1（x1,y1），顯然有y1=y0+hf(x0,y0)，再從P1出發，以f(x1,y1)為斜率作直線推進到x=x2上的一點P2，其余類推，這樣得到解曲線的一條近似曲線，它就是折線。由Euler法解法和幾何意義可知，若將圖2的坐標軸原點O移到P0點，得到圖3。可以認為函數曲線y（x）是鉆孔水平變形曲線，其中原點O為深部位移內滑面，通過深部位移測斜儀，可以測出P1、P2、······各點的變化夾角，從而得出該點的斜率值，通過計算，折線為測量的位移變形曲線。由于鉆孔水平位移的變形量和孔深相比，其值要小很多，其夾角變化的值也非常小，因此，可認為深部位移測量中各段的標準長度L和Euler法中的步長h相等。深部測斜結果中斜率值與Euler法中f（xn,y（xn））相對應，數值計算結果中y（xn）與對應。由此可知，由深部位移監測計算的變形值，就是常微分方程的Euler法數值解。

3 深部測斜儀測量誤差與分析

3.1 深部測斜儀測量誤差

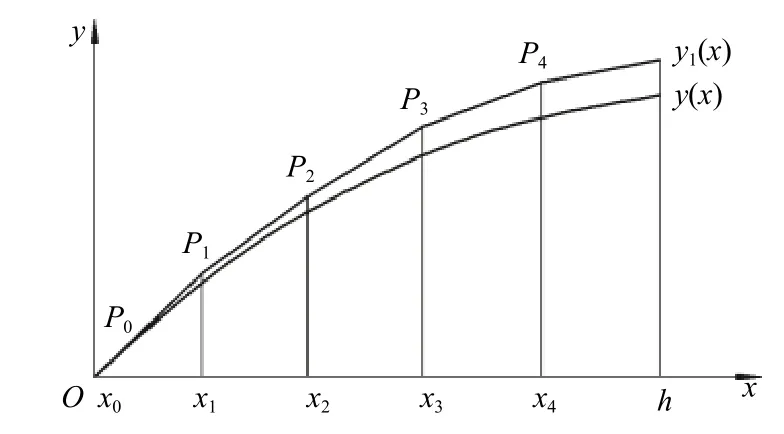
圖3 Euler法的幾何意義示意圖（原點偏移）Fig.3 Schematic diagram of the geometric meaning of the Euler method（Origin Offset）

由第2節的討論結果可知，可用常微分方程的Euler法數值解分析深部測斜儀測量結果誤差。

Euler法也可利用y（xn+1）的Taylor展開式得到：

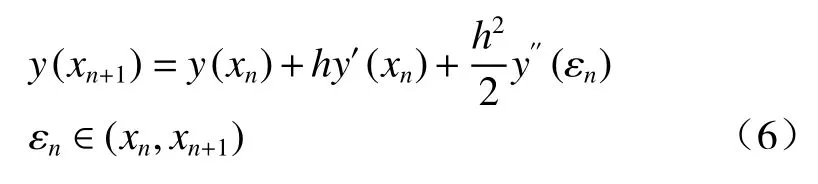
其中，由于y′(xn)=f(xn,yn)，與式（5）相比，Euler法與準確解相差，那么就是Euler法的局部截斷誤差，也即深部位移測量值的各段誤差，整體誤差就是各段誤差的累計總和（T），具體見式（7）：

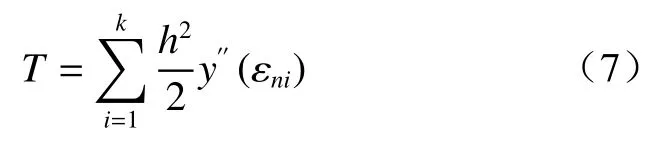
3.2 深部測斜儀測量誤差分析

（1）測量初值對誤差的影響分析

由圖3和式（6）可知，深部位移測量值的計算在初始值y0的基礎上進行，y0值的準確性決定了測量值的合理性，因此需要保證初值為0或為固定值，即要求深部位移監測孔要深入滑面以下。

（2）測量分段長度對誤差的影響分析

由式（7）可得，深部位移測量值的誤差大小與k、h和y′′(εni)有關。其中k為深部位移測量孔的分段個數，h為每個分段的長度。在總深度確定的情況下，k和h關系如下：

式中：H——測量孔總深度/m。

把式（8）代入式（7）中，得

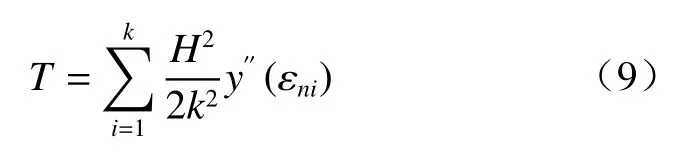
由式（9）可見，在監測孔深為定值的情況下，監測誤差與k和ni) 有關。由于在每個測量段內是在一個區間范圍內變化的值，不便于分析，因此暫定取所測量區段內的最大值，設這個最大值為y′′(εn)，那么式（9）就變為：

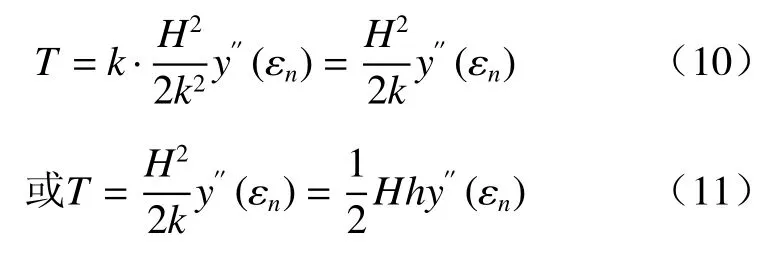
由式（10）或式（11）可知，在總深度一定的情況下，總誤差隨著測量分段個數的增加或測量分段長度的減小而減少，呈一次線性關系。當測量分段個數k→∞（或分段長度h→0）時，總誤差趨近于0。

所以，如果需要提高測量精度，就應增加測量分段個數或減少測量分段長度。

（3）變形曲線形狀對測量誤差的影響分析

為了便于分析測量分段長度對測量結果的誤差，假定y′′(εni) 為固定值，而在實際中，y′′(εni)是隨變形曲線的形狀而變化的。由于實際中變形曲線的形狀比較復雜，y′′(εni)的值無法確定，因此本節僅對簡單的曲線進行誤差分析，并假定測量孔深和監測分段個數（或分段長度）為定值。

①y′′(εni)=0

當y′′(εni)=0，y′(εni)=c(c為常數)，表明變形曲線的斜率為常數，即曲線為一直線，此時式（10）或式（11）等于0，表明監測數據誤差為0。

②y′′(εni)≠0

當y′′(εni)≠0，y′′(εni)的大小取決于深部位移變形曲線的斜率變化，當y′′(εni)同號時，同號時一般y′′(εni)＞0，由于位移變形曲線誤差是累計誤差，隨著測量次數的增加，測量誤差也累積增大。從孔底開始測量誤差向孔頂依次增大，孔內頂部最后一次測量計算的數據誤差最大。

另外，當y′′(εni)＞0，表明曲線是凹形。由式（9）知，y′′(εni)越大，計算誤差越大。說明監測變形曲線的凹形程度越大，監測計算誤差越大，孔口的變形值也越大。這表明孔口變形越大時，監測數值的誤差也越大。

4 監測曲線形狀對誤差的影響分析

在第3節分析結果可知，曲線形狀對監測數值誤差的影響較為復雜。以孔深為定值（假設為50 m），監測曲線分別為二次曲線和三次曲線條件下孔口變形和測量段數的不同進行誤差分析。

4.1 二次曲線

設位移變形曲線為y=Ax2，x為孔深（50 m），y為孔口變形值，分別以不同孔口變形量和測量段長分析誤差。

（1）孔口變形值

以孔口變形為0.5 m計算，把y=0.5、x=50代入曲線方程得A=2×10?4。假設測量段長h=0.5 m，則測量總段數k=100，得y′′=2A=4×10?4。

把上述結果代入式（10），得孔口誤差為5×10?3m，即5 mm。由此可見，測斜儀測量的誤差是較小的。依據上述方法，計算孔口水平位移在0.4，0.3，0.2，0.1 m時的誤差，結算結果見表1，可知孔口水平誤差隨孔口變形值的減少而減少，誤差約為1%。

表1 不同孔口水平位移下的計算誤差Table 1 Errors under different orifice displacement

（2）測量分段長度

以孔口變形值為0.5 m，孔深為50 m，代入式（10）計算測量分段長度不同時的誤差計算，結果見表2，可見誤差隨測量段長的增大線性增大。

表2 不同測量分段長度下的計算誤差Table 2 Errors under different length of the measuring section with conic curve

4.2 三次曲線

y=Ax3

設位移變形曲線為，x和y意義和取值、測量段長（h=0.5 m）和總段數（k=100）均同4.1節。（1）孔口變形值

把y=0.5、x=50代入y=Ax3，得A=4×10?6。

因y′′=6Ax，則y′′(εn)=6Aεn，此時，εn是一個不定的數值，以最大值來考慮計算出來的誤差偏大，趨于保守。取εn=50，y′′=1.2×10?3，

把上述結果代入式（10）得孔口誤差為15 mm。依據上述方法，計算孔口水平位移在0.4，0.3，0.2，0.1 m時的誤差，結果見表1。

（2）測量分段長度

用式（10）計算孔口變形值為0.5 m、孔深為50 m，不同測量分段長度時的誤差，結果見表2。

由表1和表2可知，在相同條件下，三次曲線的誤差大于二次曲線的誤差，原因在于數值分析中三次曲線的y′′(εni)的值比二次曲線的大，所以造成監測誤差增大。說明在深部位移監測中，曲線變形彎曲程度越大，其監測誤差越大。

5 結論

（1）深部位移監測初始值須為0或固定值。

（2）監測變形誤差與監測曲線的形狀有關。監測位移曲線為直線時，誤差等于0；監測位移曲線為曲線時，誤差的大小根據位移曲線的形狀來確定：當監測曲線為凸曲線（或凹曲線）時，其變形程度越大，誤差越大；當變形曲線為單一的凸曲線（或凹曲線），監測測量誤差為累計誤差，從孔底向孔口誤差依次增大。

（3）監測變形誤差與測量分段長度有關，測量分段長度越小，測量誤差越小，當測量段長趨近于無窮小時，誤差為0。

（4）對于相同形狀的監測曲線，孔口變形值越大，監測測量誤差越大。