基于廣義Snell 定律的聲超表面折射
楚琦琦胡 宇林 瑋
(南京航空航天大學應用物理系,江蘇南京 211100)
材料是人類社會存在的重要物質基礎,與社會生產力的發展息息相關。但傳統材料受其本身物理、化學性質的限制,無法滿足人們對其在某些場合的特殊需求。而超材料的出現沖破了傳統材料固有性質的束縛,解決了這一難題[1]。超材料[2]是一類不同于傳統材料、由亞波長人工微結構單元組成、具有特殊功能的材料,人們可以通過改變微結構的構型實現所需要的不同功能[3]。其中,屬于超材料的超表面[4-6]由于體積小,因此由其制作出相應的器件具有尺寸較小、結構簡單、低損耗等優點,得到了越來越廣泛的應用[7-9]。
2013 年,李勇等人[10]設計了類似于叉指換能器形狀折疊空間結構聲超表面,這是第1 次在亞波長尺度下利用聲超表面實現對聲波相位的有效調控,該結構各單元相位覆蓋范圍為0~2π 且規律變化,很好地模擬了聲學異常反射現象;2015 年Tian 等人[11]通過設計梯度單元聲超表面也實現了聲波的異常折射、貝塞爾波束、聲聚焦等一系列奇異現象;南京大學朱一凡等人[12]設計了一種梯度型超表面,實現了寬頻帶范圍內聲波的異常反射現象。基于前輩們的工作,可總結出由于聲波在聲超表面單元內傳播路徑的長短不同實現對其相位的調制,從而實現對聲波靈活操控的經驗。因此,文章利用一種深淺窄阱型聲超表面,較好地仿真了聲波的異常折射現象。
1 理論基礎
已知作為幾何光學的基本實驗定律之一的折射定律滿足關系式:

式中:n1、n2分別為分界面兩側介質的折射率,θi為入射波相應的入射角、θt為折射波相應的折射角,如圖1(a)所示。以上也被稱為傳統Snell 定律。
由于光波、聲波具有相似性,即滿足相似的波動方程,具有相同的波矢等波參數,故聲波也遵循上述Snell 定律。但當在兩介質分界面上引入相位突變時,入射波、折射波不再滿足普通的折射定律,如圖1(b)所示。
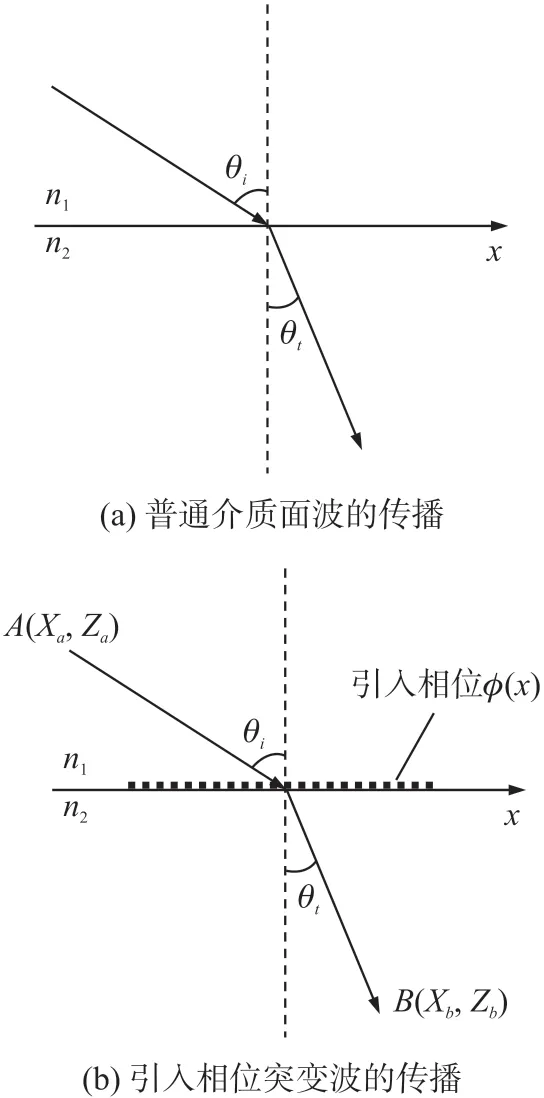
圖1 兩種折射定律示意圖
聲波從A(Xa,Za)點出發,經附帶相位φ(x)的聲超表面傳播到B(Xb,Zb)點。由費馬原理,即光沿實際光程取極小值的路徑傳播,將其應用在上述聲波傳播的路徑中,即聲波沿聲程取極小值的路徑傳播,換一種說法,聲波沿相位取極小值的路徑傳播。設分界點坐標為(X,0),聲波由A點傳播到B點的相位變化為:
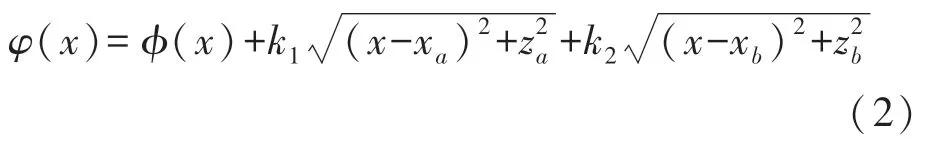
式中:k1、k2分別是入射介質面、折射介質面的波矢,且有k=2π/λ。
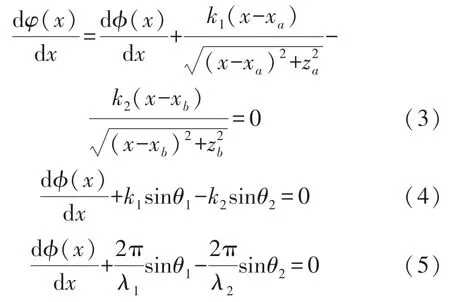
式中:λ1、λ2為入射波、折射波的波長。上式可化簡為:
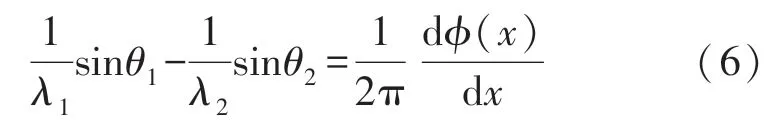
此為廣義Snell 折射定律的表達式。由式(5)可看出,當=0 時,表達式滿足普通廣義Snell定律;當≠0 時,我們可以通過適當設計的值,給定不同的入射角,獲得想要的不同折射角,達到任意控制聲波的目的。
2 構建模型
2.1 設計結構
為實現對聲波的相位調制,利用一種窄阱結構,基于聲波在聲超表面各單元傳播時路徑長短不同而使得相位不同的原理,在相鄰高矮井之間實現0 到2π 范圍的相位調制,部分結構如圖2 所示。
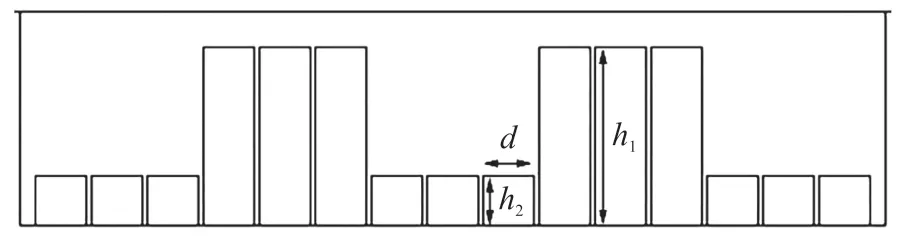
圖2 聲超表面結構圖
此結構由一排周期性的深淺凹槽構成,且每組深淺凹槽有3 個窄阱單元,其尺度設計在亞波長級別,設計參數如下:h1=35 cm,h2=9.75 cm,d=10 cm,故Δh=25.25 cm。窄阱內部填充介質1 材料鉛,窄阱外部以及上表面填充介質2 材料鐵,二者相關參數如表1 所示。

表1 介質材料參數表
聲波在深淺凹槽中傳播至分界面處的相位差為Δφ=(k1-k2)*Δh,由公式k=2π/λ,λ=c/f,其中f為入射聲波的頻率,在此我們設定8 500 Hz,可求得聲波通過相鄰凹槽后的相位差為π,則將結構排列成偶數周期型凹槽結構,可實現0 到2π 范圍的相位變化。
2.2 模擬仿真
研究方法采用有限元分析法,構建一半徑為720 cm 的圓域,將其一分為二,并將上述聲超表面結構導入到二者分界面處,然后在上下表面分別填充不同的介質,結構模型如圖3 所示。
在下表面我們給定y軸方向平面波輻射的背景壓力場,使得聲波以0°入射,且聲超表面結構左右兩側的分界面處設置硬聲壁,使入射波不透過,從而明顯地看出聲超表面對入射波產生的影響。

圖3 構建幾何模型圖
2.3 結果分析
由上述理論,當聲波以0°入射,聲波通過相鄰高矮窄井的相位差為π,而一組窄井寬度Δx為30 cm,將該數據代入廣義Snell 折射定律表達式可得折射角約為53°,仿真結果如圖4 所示。
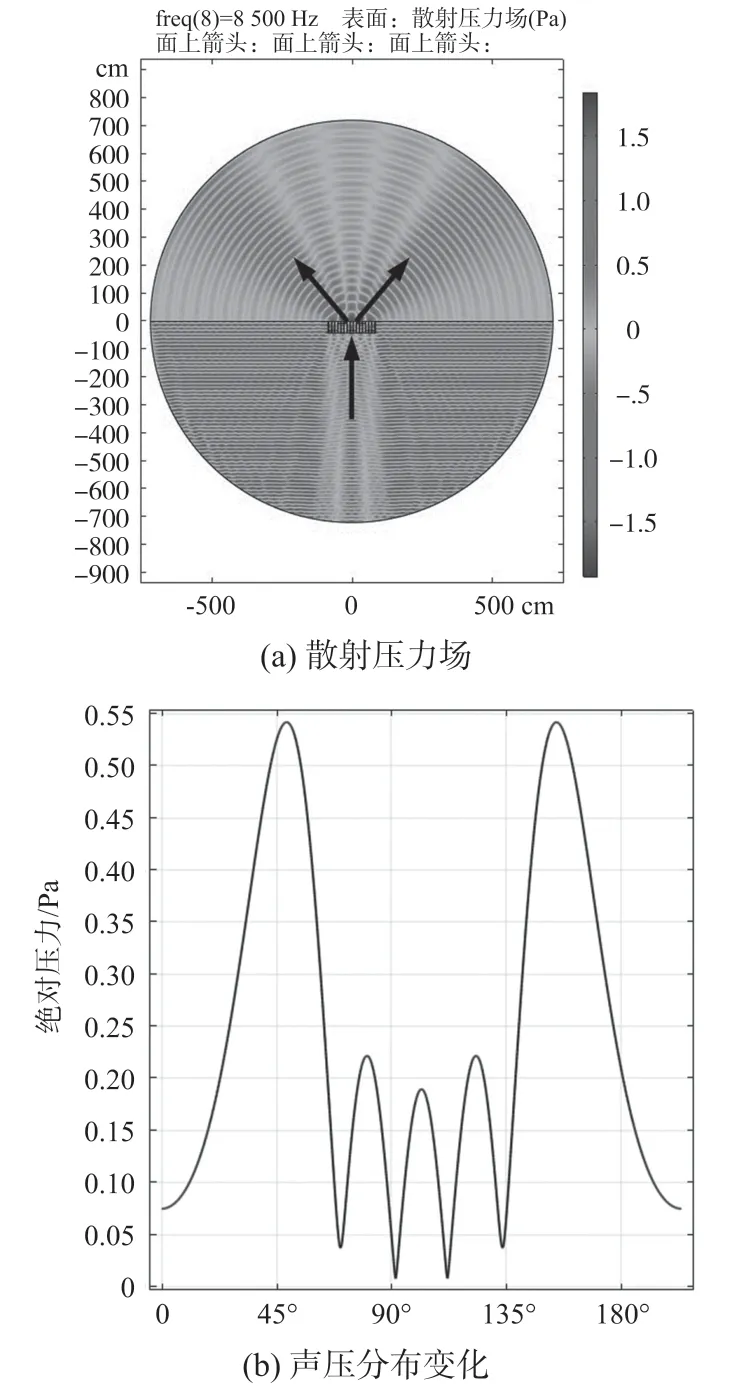
圖4 仿真結果圖
由圖4(a)、圖4(b)可以看出,實際出射聲波角度在誤差范圍內符合理論計算角度,且由于聲波通過相鄰高矮窄阱后的相位差為π,使得聲波出射有2 個方向,從而有對稱的兩束出射波,且聲壓幅值分別在約為48°、137°處表現明顯,較好地驗證了廣義Snell 折射定律。
將上述聲超表面結構進行周期性地拓展,各單元尺度大小不變,使其鋪滿兩介質分界面,如圖5所示。
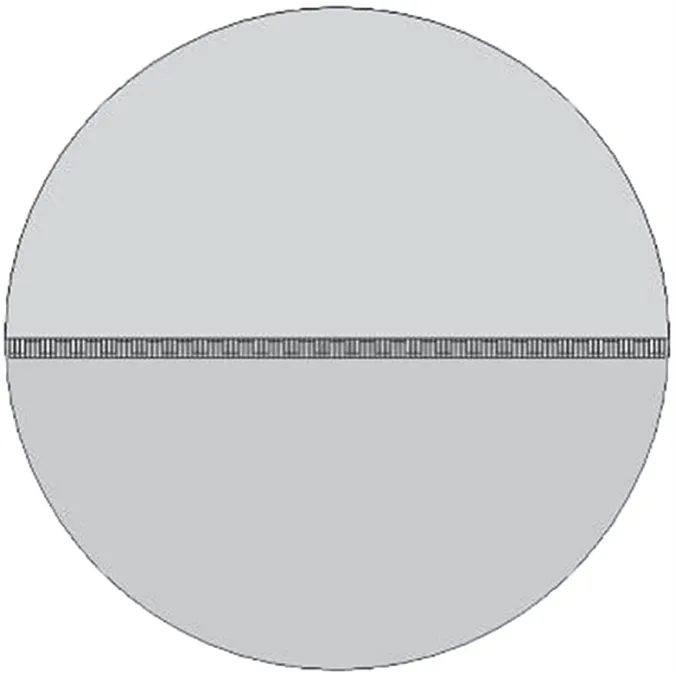
圖5 拓展周期結構模型圖
同樣在下表面給定平面波輻射的背景壓力場,且壓力幅值設為1,計算后散射壓力場如圖6 所示。
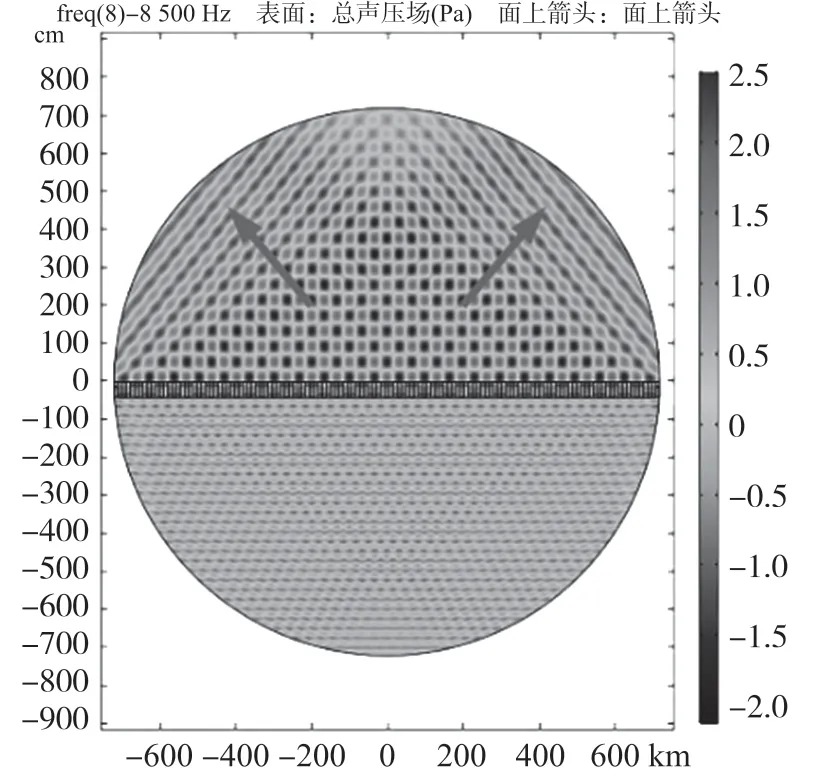
圖6 拓展周期結構散射壓力場
由圖6 可知,透過聲超表面的聲波依然遵循廣義Snell 定律,折射角符合理論計算,但與部分周期結構透過聲波不同的是,往左右方向折射的聲波交疊部分較大,若過濾一個方向的聲波,折射現象就顯得較為明顯了。
3 總結
文中利用的聲超表面結構很好地驗證了廣義Snell 折射定律,實現了聲波的異常折射。通過改變結構的參數,即窄阱的高矮比例,得到任意的波方向。此結構在設置好匹配材料的前提下,不需考慮透射率的大小,但不足之處在于頻帶范圍較窄,后期需進一步改善,實現寬頻帶折射。人們可以以上述結構為啟發,進一步地實現聲聚焦功能。

