基于改進MOPSO算法的區域偵察彈性星座重構方法
王浩,張占月,張海濤,姜平
1. 航天工程大學,北京 101400 2. 中國人民解放軍63601部隊,酒泉 732750
星座中部分衛星因故失效后重新調整星座構型的措施稱為星座重構[1],按重構方式不同可分為在軌衛星重構和發射重構。在軌衛星重構是利用星座中現有衛星重新部署;發射重構是通過發射新的衛星提升受損星座性能。對區域偵察彈性星座的重構方法進行研究,可為偵察星座的建設提供參考。
文獻[2-3]對在軌衛星重構方法進行了研究,提出了一種基于Lambert理論的星座重構方法,該方法采用Lambert轉移對衛星進行軌道機動,對機動過程中的速度增量進行了優化。文獻[4]對COMPASS導航星座的重構方法進行了研究,分別提出了利用低、中、高軌衛星和臨近飛行器對失效星座進行重構的方法。文獻[5]對以電推進方式進行軌道機動的星座重構方法進行了研究,運用組合算法解決了在星座重構過程中多星耦合機動的優化問題。文獻[6]對全球導航星座的重構方法進行了研究,對受損星座中剩余衛星采用軌道機動的方式,通過遺傳算法對調整衛星的選取及調整后衛星的相位進行了優化。文獻[7]對區域覆蓋星座的重構方案進行了研究,提出了保持軌道基本屬性和星座構型的預置量軌道機動重構方法。文獻[8]對導航星座的重構方法進行了研究,采取單顆鄰位衛星機動、兩顆鄰位衛星機動和全部衛星機動的重構策略,考慮重構能量、重構時間、能量消耗均衡度、星座的可恢復性、性能提升程度,建立了星座重構優化模型。文獻[9]對偵察星座的在軌重構方法進行了研究,考慮平均重訪時間、最大覆蓋時間,以及基于任務調度的覆蓋總時長指標,建立了重構優化模型,并提出了一種變量維數可變的多目標差分進化算法,可有效求解重構過程中機動衛星和機動目標位置耦合優化問題。文獻[10]提出發射新衛星和在軌衛星機動相結合的重構方法,通過發射衛星和在軌衛星機動形成一個新軌道面,對每顆衛星的位置及重構策略進行了優化,但并未考慮發射過程對重構的影響。文獻[11]針對通信星座的重構方法進行了研究,采取在軌衛星相位重置的方式進行,以網絡傳輸速率和延遲作為優化目標,建立了重構優化模型。
目前對星座重構方法的研究大多以在軌機動的方式對星座進行重構,該方法具有成本低、重構時間短的特點,在不考慮備份衛星機動的情況下只能減少星座性能下降程度,難以徹底恢復原有星座性能,而發射衛星重構的成本較高,重構時間與快速發射能力有關,將兩者結合進行重構的方法研究較少。本文針對區域偵察星座重構問題進行研究,提出一種一箭多星發射和在軌衛星相位機動相結合的星座重構方法。首先對重構評估指標進行分析,提出彈性指數作為星座彈性的評估指標,其次對一箭多星發射過程和在軌衛星相位機動過程進行分析,建立基于重構時間和重構成本最優的重構優化模型。針對重構優化模型中的混合變量優化問題,對傳統MOPSO算法進行改進,通過變量轉化將離散優化變量轉化為連續優化變量,提出基于學習機制的種群更新策略,并將改進的MOPSO算法應用于重構優化模型求解過程。
1 重構性能評估指標
覆蓋指標眾多,常用的覆蓋指標有覆蓋率、最大重訪時間及空間分辨率,分別衡量星座對目標空間維、時間維和質量維的覆蓋能力[12]。最大重訪時間定義為目標區域內的點連續兩次探測最大時間間隔的最大值,可通過網格點法計算[13]。本文選取最大重訪時間作為偵察星座覆蓋能力的度量指標。
重構成本按重構過程可分為發射的新衛星成本和在軌衛星機動成本,發射新衛星的成本由衛星載荷、總裝集成測試、運行控制、地面支持設備以及發射成本構成,可利用小衛星成本估計模型(small satellite cost model, SSCM)計算單顆衛星的成本Csat[14]。衛星在軌機動成本可通過衛星機動所消耗的推進劑質量來衡量,對需機動的衛星進行編號,i為編號值,由火箭方程[15]可計算出衛星i所消耗的推進劑質量mi,如下式所示。
mi=m0(eΔvi/g0Isp-1)
(1)
式中:e為自然常數;m0為衛星質量;Δvi為衛星i機動所需速度增量;Isp=300 s為火箭發動機比沖;g0=9.8 m/s2為重力加速度。
假設在軌衛星機動消耗單位千克推進劑的成本為Cm,則可計算出重構總成本C。
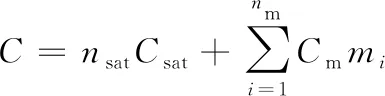
(2)
式中:nsat為新發射的衛星數量;nm為需進行軌道機動的衛星數量。
重構時間按重構過程可分為發射過程時間和在軌衛星機動時間。發射過程時間指新衛星通過一箭多星發射進入目標軌道所需要的時間,不考慮新衛星均勻部署到目標相位的時間。在軌機動時間指在軌衛星軌道機動到達目標位置所需時間。兩個過程分步進行,先發射衛星形成新的軌道面,再對在軌剩余衛星機動,保證即使衛星發射失敗,原星座構型保持不變,避免性能再度下降。重構總時間T可表示為:
T=tL+tphase
(3)
式中:tL為發射過程時間;tphase為在軌衛星機動時間。
彈性是衡量星座抗毀能力大小的指標,可通過星座受損后覆蓋能力下降程度來衡量[14]。本文更關注于覆蓋指標中最大重訪時間的下降程度,將星座受損狀態定義為星座中單顆衛星失效后最大重訪時間下降幅度最大所對應的狀態,定義彈性指數為星座從滿站位狀態到受損狀態的最大重訪時間下降幅度相對于滿站位狀態下最大重訪時間的比例,彈性指數E如下式所示。
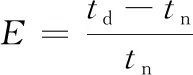
(4)
式中:tn為星座滿站位狀態下的最大重訪時間;td為星座受損狀態下的最大重訪時間。
2 基于一箭多星發射和在軌衛星相位機動的星座重構方法
采用一箭多星發射和在軌衛星相位機動相結合的方式對星座進行重構,需要考慮兩個方面,一是如何確定重構后星座的構型;二是在軌衛星如何通過相位機動到達目標位置。兩者相互耦合,需要對問題解耦,首先對一箭多星發射過程和在軌衛星相位機動過程進行分析。
2.1 一箭多星發射過程分析
通過一箭多星快速發射形成新的軌道面是恢復星座性能的一種有效手段,發射任務流程如下:1)發射準備階段:從發射任務下達開始到發射準備工作完成。2)發射等待階段:發射準備工作完成后等待發射窗口的過程。3)發射階段:從衛星發射到進入目標軌道的過程。4)調相入軌階段:衛星在目標軌道上通過調相至目標軌道相位。
對發射過程分析之前,做如下假設:
1)采用機動發射方式。
2)為節省發射成本和入軌成本,采用共面發射方式,單共切入軌方式。
3)發射衛星型號、載荷與在軌衛星相同。
為保證星座構型的相對穩定,發射新軌道面的半長軸和傾角與原星座一致,軌面內衛星均勻分布。發射過程如圖1所示,發射場經緯度(λ0,φ0),機動發射車速度為Vvehicle,機動發射區域為以發射場為圓心的球面圓形區域,其半徑由機動發射車速度和發射準備時間決定,由幾何關系可計算出機動發射區域的經度范圍[λLmin,λLmax]和緯度范圍[φLmin,φLmax]。機動發射點L的經緯度為(λL,φL),B點為L點天頂方向與目標軌道的相交點,C點為入軌點,發射新軌道面升交點赤經為Ωtar。以降軌發射為例,則從L點發射的等待時間tw為:
?(t)-λL,2π)-tp
(5)
式中:mod 表示對兩個數相除取余;Itar為發射新軌道面的傾角;?(t)為初始時刻t的格林尼治恒星時角;w′為J2項攝動下目標軌道相對于地球的旋轉角速度;tp為發射準備時間。
同理,采用升軌發射,發射等待時間tw為:
?(t)-λL,2π)-tp
(6)
經過tw+tp時后,火箭從機動發射點L發射,經發射段飛行tf后到達入軌點C。已知發射地心角為αL,將火箭發射過程近似看做兩沖量的開普勒軌道,則發射軌道上發射點L的真近點角fL=π-αL,發射軌道上入軌點C真近點角fC=π,根據軌道力學知識可得L點和C點滿足下式[16]。
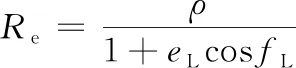
(7)
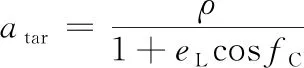
(8)
式中:Re為地球半長軸,取6 378.14 km;eL為發射軌道偏心率;ρ為發射軌道半通徑;atar為目標軌道半長軸。
式(7)和式(8)聯立解得ρ、eL,進一步求得發射軌道的半長軸aL:
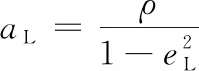
(9)
根據真近點角與平近點角的關系,可求得發射點L的平近點角μL,則可計算出發射段的飛行時間tf:
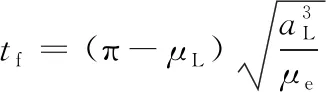
(10)
式中:μe為地球引力常數。
進入目標軌道后,新衛星按重構后的構型均勻部署于軌道面內。
2.2 在軌衛星相位機動過程分析
假設原星座各軌道面內衛星均勻分布,對存在失效衛星的軌道面內剩余正常衛星采取均勻相位的操作。如圖2所示,該軌道面內衛星6、7、8失效,剩余正常衛星通過相位機動重新形成相位均勻的相對構型。已知存在失效衛星的軌道面數為I,按升交點赤經大小進行編號,i=1,2,…,I為編號值,軌道面內的衛星按緯度幅角大小進行編號,j為編號值。第i個軌道面內第1顆衛星的緯度幅角為Mi,1,則該軌道面內第j顆衛星的緯度幅角為Mi,j,如下式所示。

(11)
式中:Qi為第i個失效軌道面內原衛星總數。
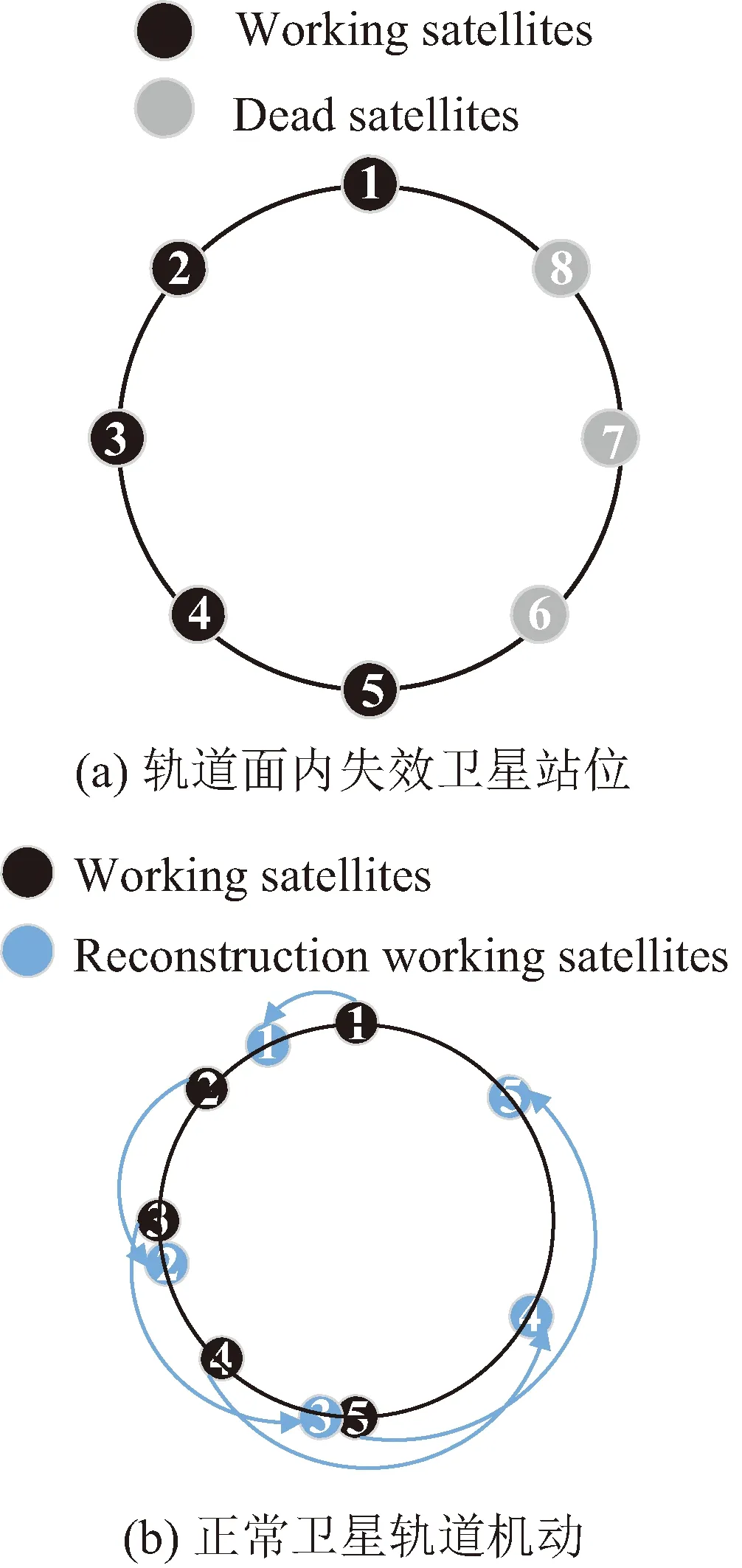
圖2 在軌衛星均勻相位Fig.2 On-orbit satellites uniform phase
除去失效衛星后,重新按緯度幅角大小進行編號,k為編號值,則該軌道面上第k顆正常衛星的緯度幅角為Mi,k。
均勻相位可采用高軌調相和低軌調相方法進行。高軌調相過程如圖3所示,衛星1從當前相位移動到目標位置,調相方式為衛星進入比目標軌道半長軸大的調相軌道,利用兩個軌道的周期不同,逐漸減小衛星1和目標位置的相位差。具體實施方式為:衛星1首先沿速度方向加速進入調相軌道,在調相軌道運行一定圈數后到達目標位置時,再施加一個沿速度反方向的沖量進入目標軌道。低軌調相過程與此相反。當調相時間固定時,調相所需速度增量與衛星相位調整量成正比,當相位調相量ΔM∈(0,180]時,采用低軌調相所需速度增量更小,當ΔM∈(180,360)時,采用高軌調相所需速度增量更小。
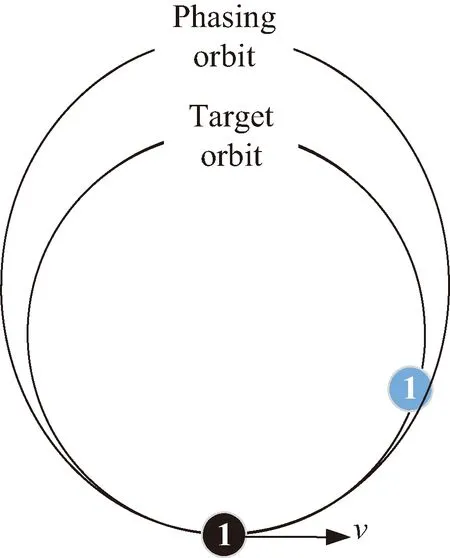
圖3 高軌調相Fig.3 High orbit phase adjustment
均勻相位后第i個軌道面第1顆衛星的緯度幅角為Ki,1,則該軌道面第k顆衛星的緯度幅角為Ki,k,如下式所示。
k=1,2,…,Qi-Si
(12)
式中:Si為第i個軌道面內失效衛星數量。
第i個軌道面第k顆衛星相位調整量為ΔMi,k=Ki,k-Mi,k。當ΔMi,k∈(0,180]時,采用低軌調相,當ΔMi,k∈(180,360)時,采用高軌調相。
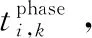
(13)
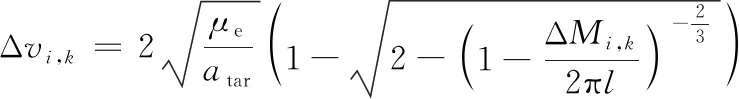
(14)
式中:Torbit為失效軌道周期。
若采用高軌調相,同理可得調相時間和調相所需速度。
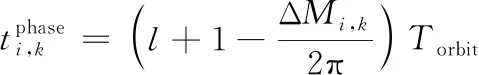
(15)
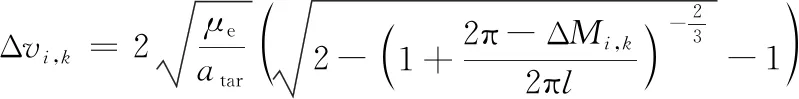
(16)
由式(1)和式(2)可計算出所有失效軌道面上正常衛星機動所需成本Cn為:
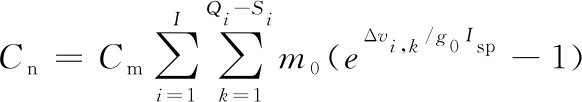
(17)
調相階段所需總時間tphase為:
i=1,2,…,I;k=1,2,…,Qi-Si
(18)
2.3 基于重構時間最優的重構優化模型
以恢復原有星座性能為目的,要求重構時間最短,建立重構優化模型,該模型主要應用于應急狀態下的重構任務。共存在5+I個優化變量:發射形成的新軌道面內衛星數S,機動發射點經度λL,發射點緯度φL,新軌道面的升交點赤經Ω以及軌道面內第1顆衛星的緯度幅角M0,第i個失效軌道面相位均勻后第1顆衛星的緯度幅角Ki,0(i=1,2,…,I)。
優化目標:
min (F,T,E)
(19)
式中:F為星座對目標區域的最大重訪時間。
優化變量:
x=(S,λL,φL,Ω,M0,Ki,0)
(20)
約束條件:
1)為保證機動發射點能夠發射目標軌道的衛星,機動發射點的緯度φL需滿足:
φL≤itar
(21)
2)由于機動發射區域為球面圓區域,機動發射車速率為Vvehicle,發射準備時間為tp,機動發射點的經緯度除滿足邊界約束外,還需滿足:
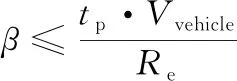
(22)
式中:β為機動發射點與發射場的地心夾角。
3)在軌衛星機動過程中,當ΔMi,k∈(0,180]時,優先選擇低軌調相機動,調相軌道半長軸ai,k需高于低軌調相所允許的最小軌道半長軸。若不滿足,則選擇高軌調相。
ai,k≥Rx
(23)
式中:Rx為低軌調相所允許的最小軌道半長軸,一般取6 678 km;ai,k為第i個失效軌道面第k顆正常衛星的調相軌道半長軸。
2.4 基于重構成本最優的重構優化模型
重構目的為最小重構成本恢復原有星座性能,適用于常規場景下的重構任務,建立星座重構優化模型。模型中的優化變量、約束條件及優化步驟與基于時間最優的重構優化模型類似,不再敘述。
優化目標:
min(F,C,E)
(24)
添加約束條件:
1)發射過程優先選用降軌發射,當發射時機不滿足降軌發射時,即降軌發射等待時間tw<0,表明無降軌發射時機,則選擇升軌發射。
2)規定重構最大時長為Tmax,則重構總時間小于重構最大時長。
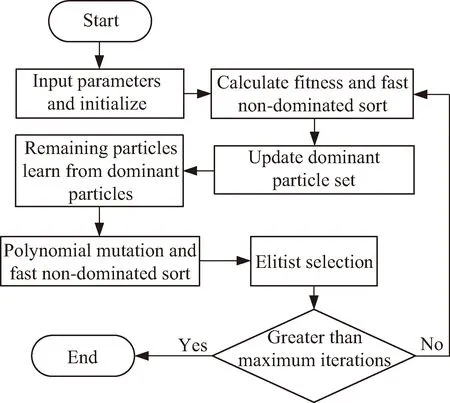
T (25) 傳統的多目標算法對離散變量優化時多采取圓整和轉化為約束條件的操作方法,而星座構型問題的離散變量一般為衛星數量和軌道面數,與軌道參數一同確定星座構型,共同影響星座的性能。若采取去圓整的方法將導致初期進化階段衛星數量和軌道面數變化太快,無法對變量空間進行充分搜索,遺漏最優解。星座問題的強非線性導致約束條件越復雜越難得到最優解,將整數變量轉化為約束條件加大了算法的收斂難度。針對這些問題,本文提出一種改進的MOPSO算法,首先通過變量轉化法將離散變量轉化為連續變量進行處理,其次利用約束支配關系將約束融入優化過程中,之后對種群進行Pereto支配排序,依據排序等級及擁擠度構建優勢子種群集合,種群中其余粒子向優勢粒子學習,算法流程如圖4所示。 圖4 MOPSO算法流程Fig.4 MOPSO algorithm flow chart 建立多目標優化模型,如下式所示。 min(f1(x),f2(x),…,fn(x)) (26) (27) 式中:f(x)為優化目標;x為優化變量;g(x)為不等式約束條件;h(x)為等式約束條件;n,m,p分別為編號值;M為不等式約束個數;P為等式約束個數。 優化算法常采用約束違反度cv來衡量解違反約束的程度,如下式所示,約束違反度越大,表明該解的適應度越差。 (28) 式中:ε為等式約束容忍值。 針對基于Pareto支配的多目標優化算法,通過約束支配關系可處理算法中目標與約束之間的關系。加入約束后支配關系如下[17],對于任意兩個解xa、xb,當xaPareto支配xb時,需滿足以下條件之一: 1)xa是可行解,xb是不可行解。 2)xa、xb都是不可行解,但cv(xa) 3)xa、xb都是可行解,xaPareto支配xb。 變量轉換是一種利用映射關系將多種不同變量轉換為同一類型變量的方法,從而有利于優化過程中對變量進行操作,常見的兩種變量為離散變量和連續變量。將轉化后的變量稱為名義變量,連續變量的轉化關系如下[18]: xr=a+bxk (29) 式中:xr為連續變量;a、b為實數;xk為名義變量,xk∈(0,1)。例如xr∈[2,7],則可通過名義變量表示為xr=2+5xk。 離散變量的轉化關系如下[18]: xI=c+d·floor(xk) (30) 式中:xI為離散變量;c、d為整數。例如xI∈[1,5],則可通過名義變量表示為xI=1+floor(4xk)。 傳統MOPSO算法需要建立外部檔案,保存粒子的歷史信息,操作復雜。本文提出基于學習機制的種群更新策略,只對當代粒子進行操作,增強了算法的收斂性。策略分為兩步,第一步構建優勢子種群。根據Pareto等級和擁擠距離選擇優勢粒子構建子種群方法如下:假設優勢子種群的粒子個數為N1(N1 第二步對種群中其余N-N1粒子進行學習操作,粒子i學習過程如下:1)隨機選擇優勢子種群中的一個優勢粒子。2)粒子i向該優勢粒子進行學習,使得種群逐漸靠近真實的最優解集。參考PSO算法中粒子速度和位置更新策略對種群進行更新,用該優勢粒子替代歷史最優粒子,用所有優勢粒子的平均值代替全局最優粒子。速度更新公式為: (31) 位置更新公式為: xi+1=xi+vi+1 (32) 對更新后的種群粒子進行變異操作,以保證種群探索新粒子的能力,一般采用多項式變異。合并原種群和更新后的種群,進行精英選擇,構成新種群參與下一代進化。 仿真時間為2021-01-01 00:00:00—2021-01-02 00:00:00,通過STK和MATLAB聯合進行仿真。原星座參數:軌道高度為500 km,軌道傾角為86°,3個軌道面升交點赤經分別為50°、108°、228°,每個軌道內8顆衛星均勻分布,3個軌道面第1顆衛星的緯度幅角分別為34°、40°、20°。每個軌道面存在2顆失效衛星,軌道參數如表1所示。 表1 失效衛星軌道參數 經STK計算,可得星座滿站位狀態下對某一區域的最大重訪時間為2.797 4×104s,彈性指數為0.48。在受損狀態下,星座對區域的最大重訪時間為3.97×104s,彈性指數為0.09。 設置初始參數如下:發射場經緯度值(100.5,41.1),機動發射車速度88 km/h,發射準備時間tp=2 h,則機動發射點經度值范圍[98.4,102.5],緯度值范圍[39.50,42.68]。衛星總質量m0=120 kg,在軌衛星機動消耗單位千克推進劑的成本Cm=200美元,火箭最大搭載量1 t,發射地心角αL=10°。在軌衛星機動階段原失效衛星運行圈數l=5。 建立基于重構時間最優的重構優化模型,并通過改進的MOPSO算法求解,得到的Pareto解集如圖5所示,圖6為Pareto解集的最大重訪時間與彈性指數的關系。 圖5 Pareto解集(時間最優)Fig.5 Pareto solution set(time optimal) 圖6 Pareto解集的最大重訪時間與彈性指數的關系(時間最優)Fig.6 The maximum revisiting time and the elastic index of the pareto solution(time optimal) 如圖6所示,陰影部分為重構后星座大于原有星座性能的重構方案,箭頭所指的重構方案的重構時間最短,為51 711 s,為重構時間最優方案。具體發射方案為需要發射6顆衛星,機動發射點經緯度值為(100.53,40.68),發射的新軌道面升交點赤經為112.32°,面內第1顆衛星的緯度幅角為49.54°。在軌衛星相位機動方案為:均勻相位后3個失效軌道面內第1顆衛星的相位分別為32.75°、11.18°、29.03°。重構后星座對該區域的最大重訪時間為2.772 2×104s,彈性指數為0.047,均優于原星座滿站位狀態下的指標值,滿足重構要求。 以重構成本作為優化目標,建立基于重構成本最優的重構優化模型。規定最大重構時長為1天,得到的Pareto解集如圖7所示,圖8為Pareto解集的最大重訪時間與彈性指數的關系。 圖7 Pareto解集(成本最優)Fig.7 Pareto solution set(cost optimal) 圖8 Pareto解集的最大重訪時間與彈性指數的關系(成本最優)Fig.8 The maximum revisiting time and the elastic index of the pareto solution(cost optimal) 如圖8所示,陰影部分為重構后星座大于原有星座性能的重構方案,箭頭所指的重構方案重構成本最少,為1.09×105美元。具體發射方案為需發射4顆衛星,機動發射點經緯度值為(101.85,40.82),形成的新軌道面升交點赤經為177.46°,面內第1顆衛星的緯度幅角為154.57°。在軌衛星相位機動方案為:均勻相位后3個失效軌道面內第1顆衛星的相位分別為32.06°、49.57°、35.77°,重構后星座對區域的最大重訪時間為2.723 6×104s,彈性指數為0.13,均優于原星座滿站位狀態下的指標值,滿足重構要求。 本文對區域偵察彈性星座的重構問題進行了研究,提出了基于MOPSO的區域偵察彈性星座重構方法,并應用于某一受損星座的重構優化中。結果表明提出的方法及算法可有效解決重構時間最優和重構成本最優兩類區域偵察彈性星座的重構問題。同時該方法也可拓展應用于通信、導航等星座的重構任務,只需將性能指標替換為通信、導航任務所關注的指標即可。本文僅分析了在軌衛星相位機動情況,除此機動方式之外,結合軌面間機動和發射考慮的重構方法可進一步進行研究。3 改進的MOPSO算法
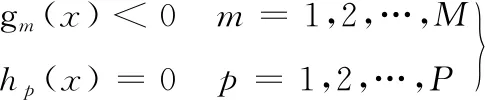
3.1 約束處理
3.2 變量轉換
3.3 基于學習機制的種群更新策略
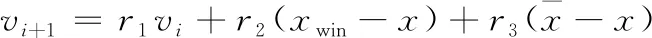
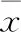
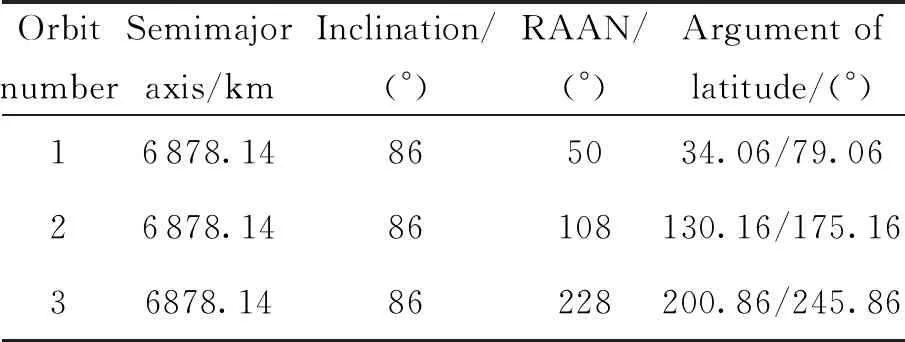
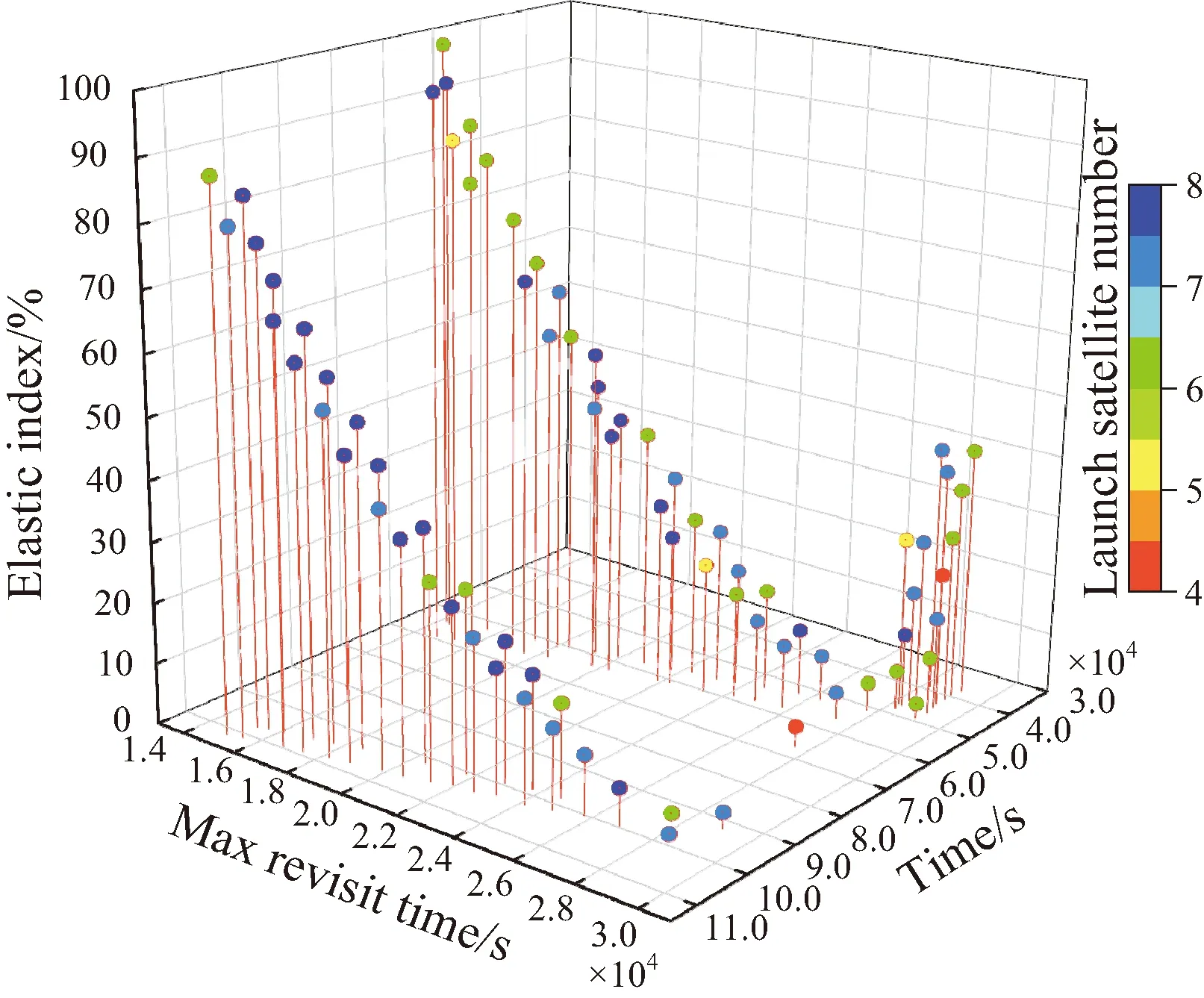
4 仿真校驗
5 結束語

