行波超聲電機振動模態非線性滑模觀測器與協調控制
荊鍇, 林夏萍, 王婕, 董硯
(1.河北工業大學 人工智能與數據科學學院,天津 300401;2. 河北省控制工程技術研究中心,天津 300130)
0 引 言
行波超聲電機(travelling-wave ultrasonic motor,TWUSM)利用壓電材料逆壓電效應激發超聲振動行波,進而使定子表面質點以橢圓軌跡運動,從而通過與轉子接觸摩擦驅動轉子旋轉。這類電機具有轉矩密度大、位置分辨率高、動態響應快、無電磁干擾等優點,在醫療衛生、航空航天等領域的精密驅動系統中得到廣泛的應用[1-4]。
由于壓電振動以及接觸摩擦的非線性,使得電機本體具有很強的非線性特征,并且電機參數也會隨著溫度變化、接觸磨損等發生明顯改變,這些因素都將影響電機的精密控制性能。針對TWUSM的非線性、時變性,現有研究多從控制算法上對電機外特性進行優化控制來提高電機運行性能。文獻[5]給出了一種非線性補償PID算法。文獻[6]則研究了帶有積分分離PID的恒定前饋和基于模型參考自適應控制的自適應反饋和前饋算法,來提高軌跡跟蹤精度。史敬灼團隊研究了采用簡單專家PID控制方法[7-8]以及非線性調節PID參數的模糊控制器[9]來改善電機速度控制。潘松、牛子杰等人則設計了模式推理控制與PID控制相融合的控制算法[10-11],實現超低速寬工作速度范圍的高精度的速度跟蹤控制。此外,H∞控制算法也被用于提高TWUSM位置控制精度[12-13]。
然而從TWUSM的驅動機理來看,定子的振動以及接觸摩擦是產生驅動轉矩的關鍵,然而,目前對TWUSM振動的研究也基于價格昂貴、不易安裝的傳感器進行電機的性能分析和模型補償[14-16],而直接用于控制的研究較少。為直接從電機振動特性上對電機運行性能給予控制優化,電機的兩相振動模態應當被重點關注。然而由于振動模態不宜直接測量,本文將采用滑模變結構觀測方法實現其重構[17-18]。滑模觀測器(sliding mode observer,SMO)具有很強的魯棒性、自適應性,適用于非線性、不確定性的系統狀態觀測,目前研究多集中在電磁電機位置觀測、飛行器狀態觀測[19-21]等。
本文將在分析合成行波與電機運行特性關聯基礎上,建立TWUSM兩相振動模態的非線性SMO,分析系統穩定性和參數魯棒性;并根據觀測的振動模態,設計協同控制算法,調節兩相電壓,進而改善電機運行特性。最后通過實驗驗證該方法的有效性。
1 TWUSM基本方程及轉矩特性分析
TWUSM的工作原理:通過給空間正交的兩相壓電振子施加兩相互差π/2的高頻正弦電壓激發兩相振動模態,進而在定子中合成行波并驅使定子表面質點的橢圓運動,從而對以一定預壓力壓在定子表面的轉子產生驅動摩擦。
TWUSM兩相電壓u=[uA,uB]T、電流i=[iA,iB]T與激發的振動模態w=[wA,wB]T間滿足以下機電耦合方程:
(1)
(2)
其中:Ms=diag{msA,msB}、Ds=diag{dsA,dsB}以及Cs=diag{csA,csB}分別代表兩相模態質量、模態阻尼和模態剛度;Rd=diag{RdA,RdB}、Cd=diag{CdA,CdB}分別為兩相壓電振子的介電損耗電阻和靜態電容;FC=[fCA,fCB]T為由于接觸作用產生的兩相界面接觸模態力;Θ為機電耦合系數。
定子中合成的行波可以表示為
(3)

近似地,定子通過接觸摩擦產生的轉矩可表示為理想轉速vid與實際轉速v之差的非線性函數[10],即
Te=fT(vid-v)=fT(φθωWsinkθT-v)。
(4)

實際中,由于電機材料、裝配等帶來的電機兩相參數非對稱性以及受運行溫度、磨損引起參數時變,即使施加的兩相電壓等幅正交,所產生的行波也將存在幅值和相位的波動,進而導致驅動轉矩的波動以及摩擦損耗的增加,影響控制性能。所以,針對兩相振動模態的觀測和協調控制是十分必要的。
2 振動模態非線性滑模觀測器設計
2.1 振動模態滑模觀測器
根據TWUSM機電耦合方程(1),由于A、B兩相表達式一致,不失一般性,將其一相方程重新寫為
(5)
其中,界面接觸模態力fC由于受電機實際運行中作用力影響,為系統不可測的非線性部分。


(6)

(7)
根據TWUSM的運行特性可知,該未知函數有界,且滿足
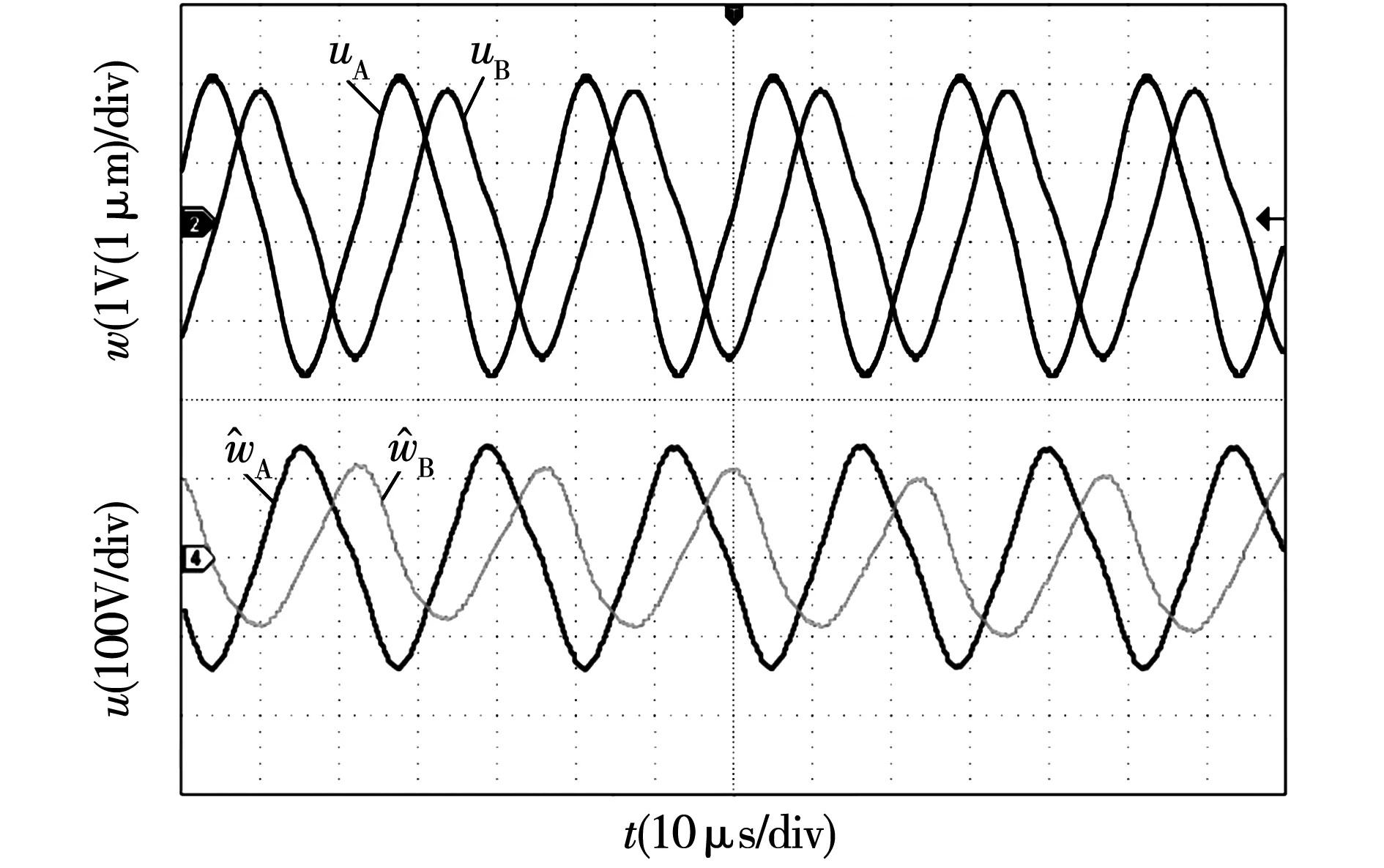
h(t,x,u)=Bξ(t,x,u),|ξ(t,x,u)| (8) 由于系統中存在非線性的未知項,根據Walcott-Zak魯棒滑模觀測器的設計方法,設計振動模態的非線性觀測器為 (9) (10) 觀測器的控制輸入為 (11) 根據系統特征及觀測器穩定性條件,對TWUSM非線性SMO的參數進行設計,得到 設Lyapunov函數 V(e)=eTPe, (12) 則有 -eTQe-ρ|fCe|-ξfCe≤ -eTQe-|fCe|(ρ-|ξ|)≤ -eTQe-|fCe|(ρ-D)。 (13) 其中第一項,Q雖然為半正定矩陣,但滿足該項沿任一軌跡不恒為零,故其平衡點為原點。第二項由于ρ≥D+η,η為正實數,也必然小于等于0,所以 (14) 等號僅在e=0時成立,于是可以證明,觀測器穩定收斂,并且對參數的擾動具有魯棒性。 根據電流方程(2),亦將其一相方程按狀態變量電壓u重新寫為 (15) (16) 其中,k1>0,0 (17) 則其一階導數 (18) (19) 結合Lyapunov函數,可以得到 (20) 則系統不僅是全局范圍內漸進穩定,而且是有限時間穩定,穩定時間依賴于s的初值s0,即 (21) (22) 對于上述觀測器中,均可采用sigmoid函數或者雙曲正切函數代換符號函數sgn(·),以降低觀測過程中的抖振。 針對TWUSM全橋驅動器,提出了一種適用于FPGA的兩相振動模態協調控制的實現方法,控制結構如圖1所示。 圖1 基于非線性SMO的振動模態協調控制圖Fig.1 Nonlinear SMO based vibration mode coordination control block (23) 這樣,通過計算獲得每相每次存儲的N個點中的峰值wAm和wBm及其對應的位置idxA、idxB分別對幅值和相位進行協調控制。 對于幅值,比較觀測得到的兩相振動模態的峰值wAm和wBm,利用PI控制下一定范圍內協同調節兩相方波電壓占空比dA、dB。兩相的占空比的初值選取方波能量利用率最大時對應的占空比37.1%[22],調節范圍按能量利用率設置為25%~50%。 對于相位的調節,則以A相為參考,調節B相相位。根據峰值所對應的位置idxA和idxB,可計算出振動模態的相位差 (24) 通過PI調節器調節B相電壓相位,使φ滿足±π/2(符號“±”表明電機正反轉需求的相位關系)。 依據上述兩相振動模態的幅值和相位的協同調節,則可實現兩相振動模態的等幅正交,降低合成行波的波動,從而減小轉矩脈動及多余的摩擦損耗。 進一步地,為實現TWUSM的精密伺服控制,在以上述振動模態的協調控制作為內環控制的基礎上,可結合以頻率調節和直流母線電壓補償的控制形式來完成外環速度/位置精密伺服控制。 仿真和實驗中所用參數均取自一臺GTUSM-60-R型TWUSM及自制電機全橋驅動控制器,電機部分參數見表1。 表1 行波型超聲電機參數 在MATLAB/Simulink中建立TWUSM及其全橋驅動器仿真模型。對照實際電機驅動狀態,設置全橋電路輸出的方波電壓頻率為42.08 kHz,占空比37.1%,幅值70 V,A相電壓滯后B相π/2,空載運行。按本文方法建立非線性SMO觀測振動模態。 圖2 起動初期兩相振動模態觀測曲線Fig.2 Observation curves of two-phase vibration modes at the beginning 圖3 穩態兩相振動模態觀測曲線Fig.3 Observation curves of two-phase vibration modes at steady state 為驗證該非線性SMO系統的魯棒性,當參數存在20%的擾動時,重新進行上述仿真。為了快速檢驗,設置A相參數增加20%,B相減少20%,得到的仿真結果如圖3所示。圖中,兩相實際振動模態曲線為實線,觀測曲線為虛線,為便于觀察,觀測曲線同樣向上平移0.5 μm。圖中可以看出,兩組曲線與未改變參數前,幾乎沒有變化,其觀測值的相對誤差依然不超過2%。 圖4 觀測器參數擾動下兩相振動模態觀測曲線Fig.4 Observation curves of two-phase vibration modes under disturbance of parameters 通過上所述仿真結果說明,本文所提出的TWUSM振動模態非線性SMO能夠快速、準確地觀測振動模態,并具有參數魯棒性,從而為優化電機控制奠定基礎。 建立協調控制仿真模型,對所提出的SMO兩相振動模態協調控制方法進行仿真驗證。 首先,未加入協調控制,仿真參數設置與上一小節相同,得到穩態時的兩相電壓、兩相振動模態以及轉速、轉矩的曲線,如圖5所示。 圖5(a)最上部分給出了兩相電壓曲線,由于全橋驅動電路兩相諧振電感以及電機兩相靜態電容參數并不完全相同,即使方波電壓的幅值、占空比設置相同,通過LC諧振得到的機端兩相電壓也不盡相同。其中A相電壓幅值為185.58 V,B相電壓峰峰值為171.19 V。下邊兩幅圖分別給出了兩相電壓幅值的偏差及兩相電壓的相位差(依算法按周期統計),其中,平均幅值偏差為14.1748 V,平均相位差為-0.493 8π。可見兩相電壓幅值接近,相位差基本為-π/2。 圖5 未加入協調控制TWUSM運行特性曲線Fig.5 TWUSM running characteristic curves without coordination control 在圖5(a)電壓作用下,仿真得到兩相振動模態曲線如圖5(b)最上部分所示,其中,兩相振動模態的幅值分別為:wA=1.251 4 μm,wB=1.593 9 μm。其幅值存在較大偏差,平均幅值偏差為-0.342 3 μm;A相相對于B相的相位差平均值為-0.507 2π rad,接近-π/2。引起振動模態幅值不相等的主要原因即電機兩相結構參數不對等。 由于兩相振動模態幅值存在偏差,將引起轉矩脈動和轉速波動,如圖5(c)所示。空載運行下,電機輸出轉矩平均值為0,但是其轉矩脈動ΔT達到0.84 N·m,相對于該型號電機最大輸出轉矩1.6 N·m,其脈動大。由此也帶來了轉速的波動:轉速均值約85 r/min,轉速的波動Δn約在1.03 r/min左右,雖然傳統意義上該轉速波動不大,但對于超聲電機低速、精密運動控制,還是將導致控制精度下降等問題。 采用本文所提出的振動模態協調控制策略,構建振動模態的幅值和相位閉環協調控制。在與上文相同的頻率和方波電壓幅值的條件下,兩相方波電壓的占空比分別經控制調節為A相46.2%、B相28.0%,相位差為-0.49π。穩態下,兩相電壓、兩相振動模態以及轉速、轉矩的仿真曲線分別如圖6所示。 調節后,機端兩相電壓發生了較大變化,如圖6(a)所示,兩相電壓的幅值分別為:A相201.25 V,B相138.09 V,幅值偏差64.42 V,相位差則變化為-0.485 8π。而兩相振動模態,如圖6(b)所示,呈現出等幅正交的狀態,兩相振動模態的幅值分別為1.359 8 μm和1.361 7 μm,平均幅值偏差僅3.730 1 nm,相對于幅值不到0.28%。兩相振動模態的平均相位差則-0.493 4π,更接近于-π/2。 通過兩相振動模態的調節,電機輸出的轉速轉矩特性得到改善。如圖6(c)所示,由于電機空載,穩態轉矩的平均值為0,轉矩脈動ΔT降至0.064 0 N·m,為未調節時的轉矩脈動的7.6%,可見轉矩脈動得到顯著降低。與此同時,速度開環轉速均值約83 r/min,轉速波動Δn降為0.268 2 r/min,性能亦得到了顯著改善。 綜上,由協調控制仿真結果可知,基于所提出的非線性SMO觀測振動模態,協調控制兩相振動模態使之等幅正交,可有效改善電機輸出轉矩和轉速的性能,進一步提升TWUSM在精密運動系統中的精密性和穩定性。 采用如圖7所示的基于FPGA的TWUSM全橋驅動控制實驗平臺進行實驗驗證,其中,TWUSM同軸連接扭矩傳感器和編碼器用于轉矩和轉速的測量,末端連接磁粉制動器用于加載。另外,實驗中將FPGA控制器中所觀測到的振動模態通過DAC輸出,從而便于直接觀測。 圖6 加入協調控制TWUSM運行特性曲線Fig.6 TWUSM running characteristic curves with coordination control 未加協調控制時,全橋驅動器輸出方波電壓占空比37.1%,頻率42 kHz,磁粉制動器未加載(空載)。穩定運行,通過編碼器獲得電機轉速約為89 r/min,電機電壓和觀測振動模態波形如圖8所示。其中,A、B兩相電壓幅值分別為190 V和172 V,觀測到的振動模態幅值分別為1.43 μm及1.10 μm,相位差0.538 9π。兩相振動模態幅值存在有0.33 μm偏差。 圖7 基于FPGA的TWUSM全橋驅動控制實驗平臺Fig.7 FPGA-based full-bridge drive control platform of TWUSM 圖8 未加入協調控制電壓、振動模態曲線Fig.8 Voltage and vibration modes curves without coordination control 加入協調控制后,兩相占空比經控制調整為A相30%、B相46%,空載下轉速約為87 r/min,電壓及觀測振動模態波形如圖9所示。其中,兩相電壓幅值分別調節為130 V和203 V,獲得觀測的振動模態幅值分別為1.35 μm和1.34 μm,相位差為0.494 4π,實現了模態的等幅正交。 上述兩組實驗所對應的軸上輸出轉矩曲線通過波形記憶功同時顯示,如圖10所示,T1為未加協調控制的轉矩,T2為加入協調控制后的轉矩,由于均在空載下,其轉矩平均值近似為0。在圖中可以看出,T2轉矩脈動約為0.4 N·m,而T1的轉矩脈動達到1.4 N·m,明顯大于T2的轉矩脈動。 圖9 加入協調控制電壓、振動模態曲線Fig.9 Voltage and vibration modes curves with coordination control 圖10 輸出轉矩對比曲線Fig.10 Output torque comparison 對比上述實驗結果,如圖11所示,未引入協調控制而按等占空比進行控制,電機兩相電壓接近,但是受電機參數不對稱的影響,激發出的兩相振動模態存在較大偏差,其輸出轉矩亦存在較大脈動;而利用非線性SMO針對電機的兩相振動模態實施協調控制,使其振動模態近乎等幅正交,可有效減小電機輸出的轉矩脈動。上述實驗也間接證明了所觀測得到的振動模態的正確性。 圖11 實驗結果對比Fig.11 Comparison of experiment results 本文著眼于TWUSM產生驅動的振動本質,在分析了振動模態對輸出轉矩的影響上,研究了TWUSM振動模態非線性SMO及其協調控制策略。首先,針對不易直接測量的振動模態,在對振動模態一階導數估計的基礎上構建了一種非線性SMO設計方法,利用Lyapunov法對其穩定性以和參數魯棒性給予證明。其次,在非線性SMO的基礎上,提出了一種面向全橋驅動器的兩相模態協調控制的優化策略。最后,對所提出的非線性SMO的準確性和魯棒性進行了仿真驗證,并針對電機兩相振動模態的協調優化控制行了對比仿真和實驗。結果表明,基于所提出的非線性SMO準確獲得電機振動模態,并協調控制使其等幅正交,能有效減小電機輸轉矩脈動,提高電機運行性能。
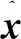




2.2 振動模態一階導數的估計



3 基于SMO的振動模態協調控制


4 仿真及實驗
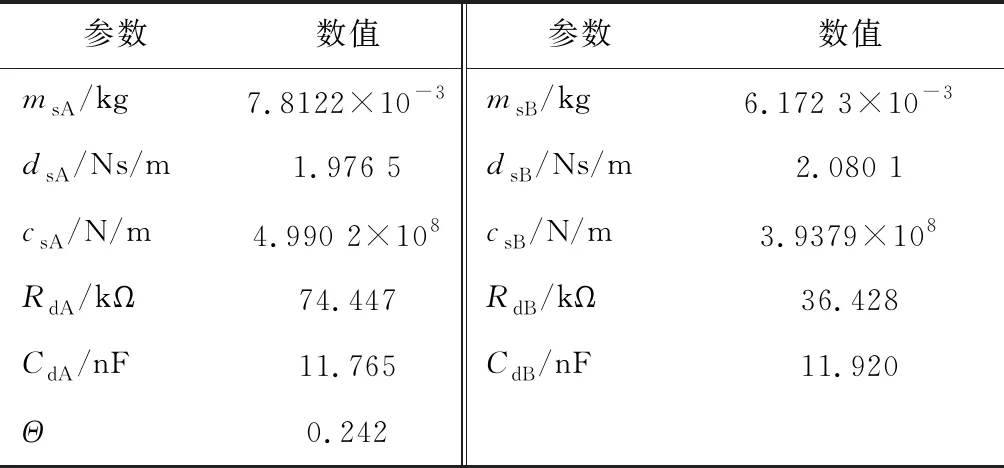
4.1 電機參數
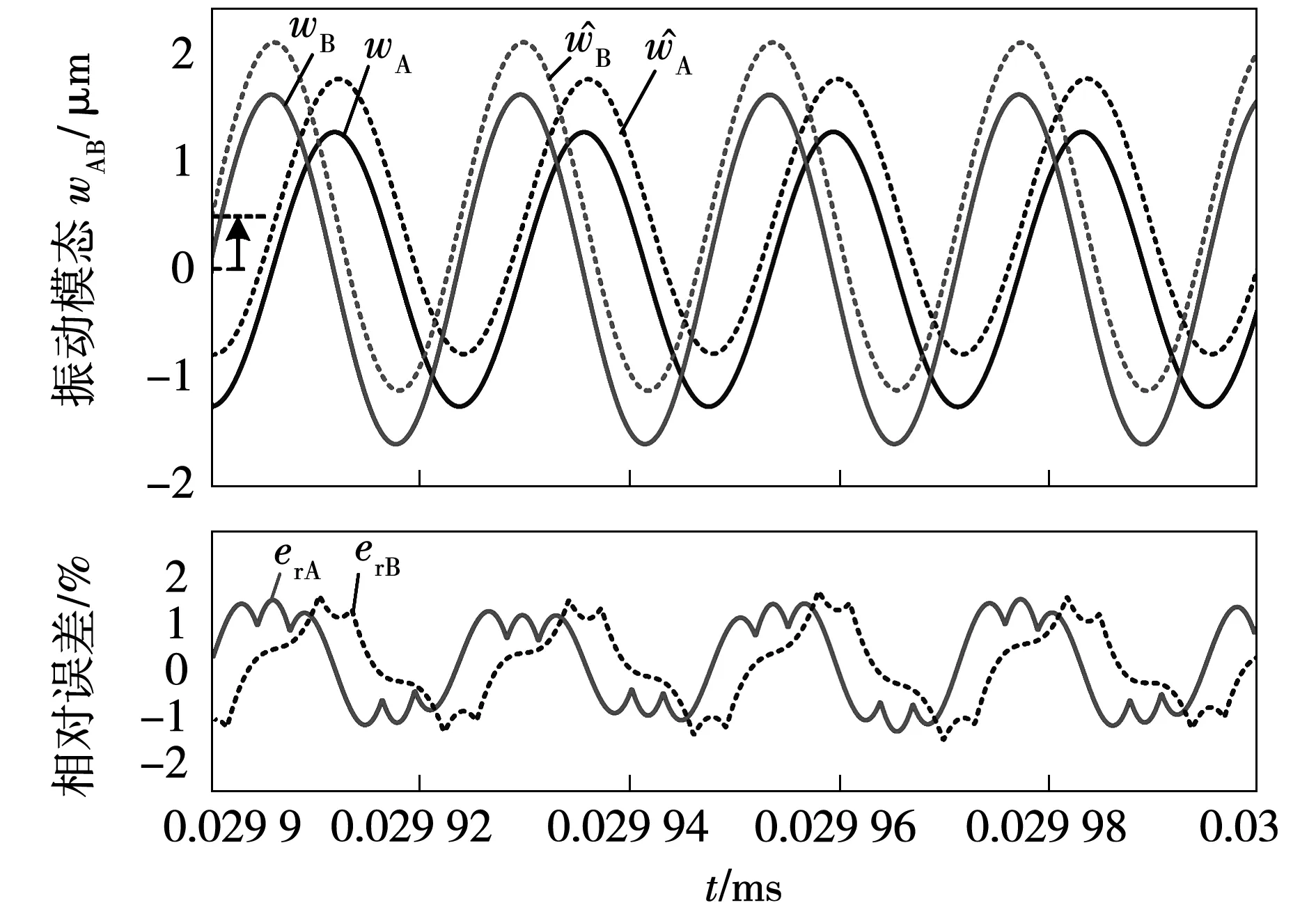
4.2 振動模態觀測器仿真




4.3 基于SMO的兩相振動模態協同控制仿真

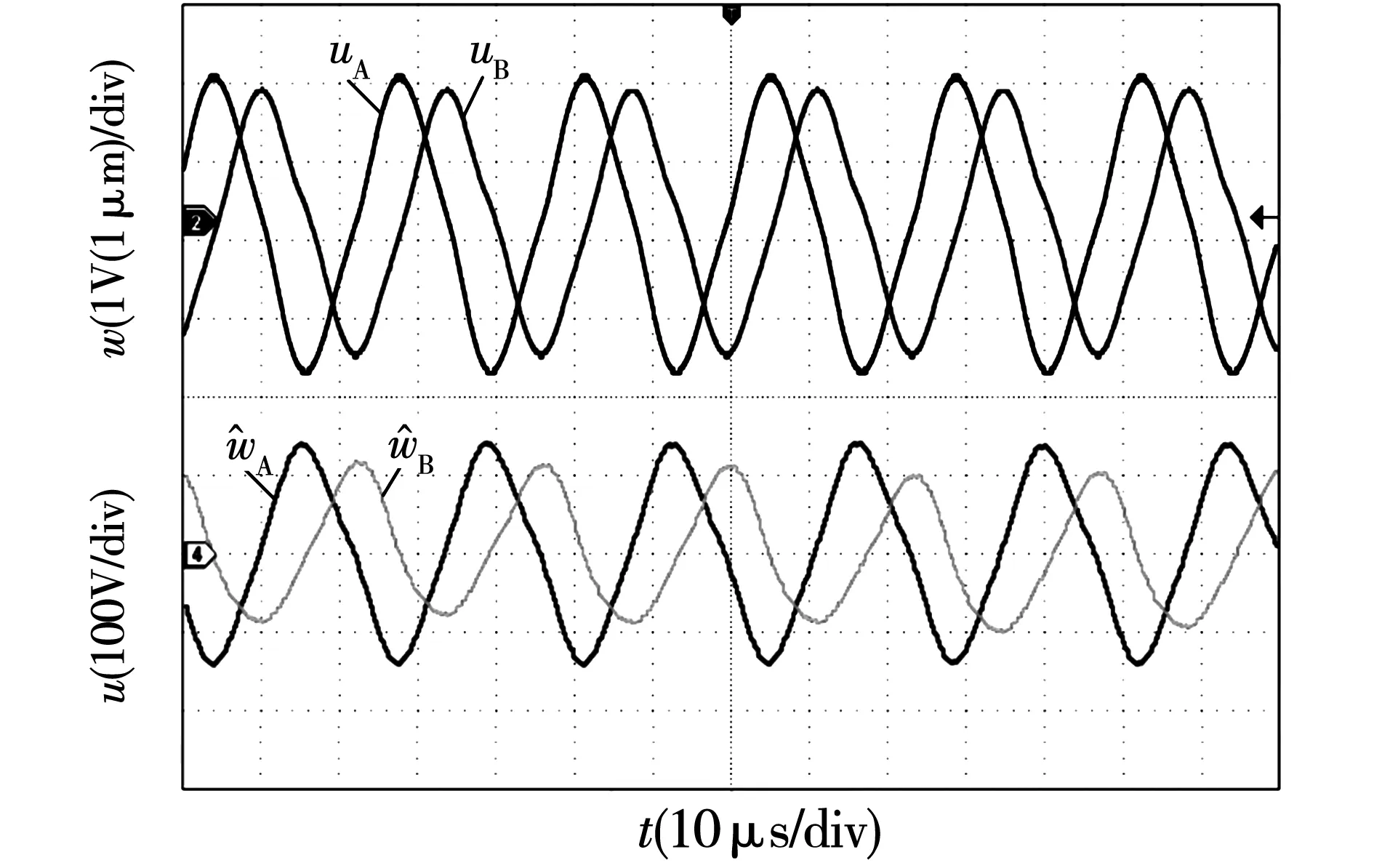
4.4 振動模態非線性SMO及協調控制實驗驗證




5 結 論

