后建構課堂的章尾復習課設計

鐘鳴　張泉

摘要

近年來，對課堂教學的研究，逐漸從章中課拓展到章首課和章尾課，分別對應“前建構”“中建構”和“后建構”，進而形成了完整的整章教學系統(tǒng)。現(xiàn)以“中心對稱圖形——平行四邊形”章尾復習課為例，具體闡述“后建構課堂”的內(nèi)容和方法：建構基礎知識結構、建構思想方法結構、聚焦能力素養(yǎng)立意。

關鍵詞

后建構課堂 章尾復習課 中心對稱圖形 平行四邊形

一、比賽之后的思考

2017年11月，江蘇省青年教師優(yōu)秀課（初中數(shù)學）從“前建構”視角確定賽題;2018年11月，江蘇省青年教師教學基本功大賽（初中數(shù)學）從“后建構”視角確定賽題。賽后總結會上，董林偉先生介紹：學習的一般規(guī)律是，先進行“前建構”，再局部深入，最后通過反思進行“后建構”，形成整體認識。

他認為，“前建構”要解決三個問題：為什么學（知識的重要性與必要性），學什么（知識技能、思想方法），怎么學（提供學習基本線索、基本支架）。相應地，筆者認為，“后建構”也要解決三個問題：知識之間有何實質(zhì)性聯(lián)系（基礎知識結構），這些知識如何運用（思想方法結構），知識運用的智慧在哪里（能力素養(yǎng)立意）。

事實上，章尾課通常包括數(shù)學活動、數(shù)學實驗、綜合實踐、章復習課等課型。本文以“中心對稱圖形——平行四邊形”的復習為例，具體闡述后建構課堂的章尾復習課的設計方法。

二、后建構課堂的設計

從“后建構課堂”的視角來看章尾復習課，首先要“建構基礎知識結構”，其次要“建構思想方法結構”，最后要“聚焦能力素養(yǎng)立意”。

1.建構基礎知識結構。

在此之前，學生已學習了“圖形的平移”“軸對稱和軸對稱圖形”，積累了一定的圖形運動變化的學習經(jīng)驗，在此基礎上，本章繼續(xù)發(fā)展了學生的空間觀念、幾何直觀、分析推理等數(shù)學素養(yǎng)。

在本章的章首課和章中課中，教師從生動的現(xiàn)實情境出發(fā)，通過操作、實驗、觀察、思考、交流等數(shù)學活動，引導學生經(jīng)歷合情推理和演繹推理的探索過程，學生初步具備了探尋知識之間內(nèi)在聯(lián)系的基本能力、運用單個知識的能力以及對一些簡單問題進行抽象、推理、探究的活動經(jīng)驗。但是，知識體系在學生頭腦中還未形成，存在模糊不清的地方（如四種特殊四邊形之間的關系）、似是而非的地方（如判定和性質(zhì)的混淆）、記憶不深的地方（如中點四邊形的形狀等），有些方法（如中點的聯(lián)想、模型的遷移等）還不夠熟練，有些能力（如運用運動變換解決問題）比較薄弱。復習前，孤立、分離的知識和模糊的認識，有必要整理，串線，連片，結網(wǎng)，縱橫聯(lián)系形成系統(tǒng)，分析并建立整章的系統(tǒng)知識結構。

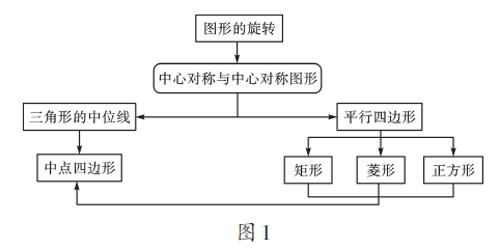
例如，本章內(nèi)容由三塊組成：探索圖形的旋轉(zhuǎn)、中心對稱與中心對稱圖形的性質(zhì);平行四邊形、矩形、菱形及正方形的性質(zhì)與判定;利用圖形的旋轉(zhuǎn)研究三角形的中位線。教材以中心對稱為主線，展開對平行四邊形和三角形中位線這兩個方面的研究，其中將平行四邊形特殊化，分別研究了矩形、菱形、正方形的性質(zhì)與判定，還將三角形的中位線進行拓展，研究了特殊四邊形的中點四邊形的形狀。教師分析并建立整章的系統(tǒng)知識結構（如圖1），有助于全面考慮教學內(nèi)容，有針對性地設計復習環(huán)節(jié)，促進學生把握知識之間的內(nèi)在聯(lián)系，對一章內(nèi)容形成整體而系統(tǒng)的認知。如此，就把握了本章的整體知識結構。

2.建構思想方法結構。

加強數(shù)學思想方法的培養(yǎng)，是全面提高學生數(shù)學素質(zhì)的重要途徑。在關注知識整體建構的同時，更要關注知識結構賴以形成的思想方法。

數(shù)學學習不僅包括知識結果，更包括結果形成過程中的思想方法。在一章學習中，學生既經(jīng)歷了知識的形成過程，也經(jīng)歷了知識的運用過程，體會一章的主導思想方法在“獲取數(shù)學知識、運用數(shù)學知識、解決問題”中的作用，是“溫故知新”的“新”之所在。在章尾課中建構思想方法結構，更能引導學生“用數(shù)學的方式理解世界”，感受數(shù)學學習的內(nèi)在魅力。

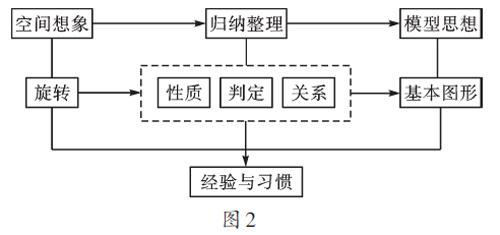
本章中，借助旋轉(zhuǎn)探究圖形的性質(zhì)，理解旋轉(zhuǎn)運動，需要空間想象;探索特殊四邊形的判定、理清特殊四邊形之間的關系，需要觀察操作、歸納猜想和推理;分析復雜的圖形，往往需要從中剝離基本圖形，需要模型思想;運用性質(zhì)判定進行問題的解決，往往需要借助圖形的運動、條件的轉(zhuǎn)化、模型的遷移等方法。對這些思想方法的揭示（如圖2），有利于知識與能力的鞏固和提升，使其內(nèi)化為學生的解題經(jīng)驗與思維習慣。

3.聚焦能力素養(yǎng)。

2011年版《義務教育數(shù)學課程標準》（以下簡稱“課標”）指出：“數(shù)學是人類文化的重要組成部分，數(shù)學素養(yǎng)是現(xiàn)代社會每一個公民應該具備的基本素養(yǎng)。”后建構課堂強調(diào)對學習過程的反思和對應用過程的體悟，重視對知識的綜合貫通、靈活組合和創(chuàng)新應用，教學立意更關注知識的應用價值以及知識運用中蘊含的思想方法，訓練高階思維，增強創(chuàng)新能力和實踐能力。

本章突出了圖形的旋轉(zhuǎn)運動。一方面作為知識的起點，串聯(lián)了中心對稱的性質(zhì)、特殊四邊形的性質(zhì)、中位線的性質(zhì);另一方面作為解題思路的起點，利用旋轉(zhuǎn)，轉(zhuǎn)移邊或角的位置，體現(xiàn)了轉(zhuǎn)化的思想。這兩方面對落實“幾何直觀”“推理能力”“模型思想”等數(shù)學核心素養(yǎng)有重要價值。

4.課堂教學環(huán)節(jié)設計。

基于上述分析，本章章尾復習課的教學目標確定如下：（1）回顧本章所學內(nèi)容，能從旋轉(zhuǎn)的角度梳理幾種平行四邊形之間的關系，對本章知識有全面、系統(tǒng)的認識;（2）以旋轉(zhuǎn)運動為突破口，進一步掌握分析、推理的思考方法，熟練掌握綜合法的書寫格式;（3）經(jīng)歷圖形運動變換的過程，積累解決問題的經(jīng)驗，進一步發(fā)展空間觀念。其中，目標（1）為重點，目標（2）為難點。設計簡案如下。

環(huán)節(jié)1 建構系統(tǒng)知識結構

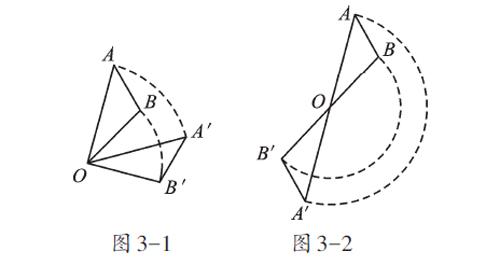
問題1 觀察圖3-1中△AOB的運動，你能找到哪些等量關系？

問題2 若將旋轉(zhuǎn)角度定為180°，如圖3-2，你能找到哪些其他的關系？

問題3 你能以文字的形式歸納旋轉(zhuǎn)、中心對稱的性質(zhì)嗎？

【說明】通過幾何直觀，在觀察的基礎上喚起記憶，回顧并梳理旋轉(zhuǎn)及中心對稱的定義、性質(zhì)，培養(yǎng)學生的歸納概括能力。

問題4 利用中心對稱的性質(zhì)，我們是如何研究特殊四邊形的性質(zhì)的呢？閱讀教材八年級下冊第64—65頁，以探究平行四邊形的性質(zhì)為例，用你自己的話說說研究的思路。

【說明】重讀教材，既體會數(shù)學研究方法，建構中心對稱與平行四邊形的聯(lián)系，又引導學生重視教材學習的基礎作用。

問題5 填表——梳理平行四邊形與矩形、菱形、正方形的性質(zhì)。

【說明】表格能更直觀地做對比。通過四個方面的比較，梳理四類特殊四邊形的性質(zhì)的異同點，幫助學生理清模糊點和混淆點。

問題6 如圖4，利用中心對稱的性質(zhì)，我們還研究了三角形的什么問題？

問題7 畫一些不同形狀的四邊形，分別連接它們四邊的中點構成四邊形（叫作中點四邊形），說說中點四邊形分別是什么形狀，并說明理由。

【說明】通過中心對稱回顧中位線的性質(zhì)，并運用中位線的性質(zhì)拓展中點四邊形的知識，完善整章知識結構。

環(huán)節(jié)2 建構思想方法結構

例1 如圖5，將△ABC繞點B逆時針旋轉(zhuǎn)60°得到△DBE，再將△ABC繞點C順時針旋轉(zhuǎn)60°得到△FEC，連接DA、EF。求證：四邊形ADEF是平行四邊形。

變式1 如果AB=AC，四邊形ADEF是何特殊四邊形？

變式2 如果∠BAC=150°，四邊形ADEF是何特殊四邊形？

變式3 △ABC滿足什么條件，四邊形ADEF會是正方形？

問題：平行四邊形與矩形、菱形、正方形有何關系？

【說明】在問題解決過程中領悟四類特殊四邊形之間的聯(lián)系，挖掘解決問題的基本方法，積累旋轉(zhuǎn)問題的解決經(jīng)驗，滲透從特殊到一般的數(shù)學歸納思想，達成學習目標（1）。

例2 如圖6，在正方形ABCD中，點P、Q分別在邊AB、AD上，且CQ平分∠DCP。求證：CP=BP+DQ。

問題：有其他方法解決問題嗎？

【說明】指向目標（2），鼓勵學生大膽想象、大膽嘗試，從旋轉(zhuǎn)運動的角度尋找解決問題的突破口，積累解題經(jīng)驗，感悟圖形運動中的不變量，體悟“圖形運動是演繹推理思路的源”，同時與等腰三角形知識相關聯(lián)，打通數(shù)學內(nèi)部不同章節(jié)知識之間的內(nèi)在聯(lián)系，培養(yǎng)綜合運用的能力。

例3 如圖7，四邊形ABCD為正方形，△CEF為等腰直角三角形，連接AE、AF，M是AE的中點，DM的延長線交AF于點N，求證：DN⊥AF。

問題1 你能用思維導圖的形式表達你對“中點”的聯(lián)想思路嗎？

問題2 對于“中點”，你還能聯(lián)想到什么？有其他方法解決此題嗎？

【說明】例3是本節(jié)課的難點——題目條件、結論看似零散，它們之間如何建立聯(lián)系？引導學生經(jīng)歷聯(lián)想與轉(zhuǎn)化的有序思維串是突破問題的關鍵，例如中點→中位線→平行線→角關系→互余→垂直。引導學生在交流中碰撞思維，加深對運用旋轉(zhuǎn)理解圖形、解決問題的認識。教師還可以提煉△BFC與△DCE構成的“手拉手模型”，培養(yǎng)模型思想，為以后解題積累經(jīng)驗。

環(huán)節(jié)3 建構能力素養(yǎng)結構

經(jīng)過本節(jié)課的復習，你對旋轉(zhuǎn)或本章知識有了哪些新的認識？對于今天的解題，你有何感受？

【說明】知識再認識、方法再提煉、思想再升華、能力再提高是復習課中最重要的方面。引導學生對課堂學習進行小結，反思數(shù)學學習過程，體悟應用過程，幫助學生積累基本活動經(jīng)驗，感悟基本數(shù)學思想，提升數(shù)學情感，豐富和完善能力素養(yǎng)結構。

三、課例設計說明

“后建構課堂”的章尾復習課強調(diào)在整體把握整章知識的基礎上，遵循學生的認知規(guī)律，將點狀知識縱橫聯(lián)系，形成結構。深入挖掘知識形成和應用過程中所蘊含的思想方法，建立思想方法結構，發(fā)展能力素養(yǎng)，提高單元復習效益。

本節(jié)課以旋轉(zhuǎn)為切入點，利用現(xiàn)代信息技術手段，呈現(xiàn)出生動活潑的動態(tài)畫面，豐富了學生的幾何直觀，為梳理幾類特殊四邊形的性質(zhì)，建構系統(tǒng)知識結構提供了有利條件;以旋轉(zhuǎn)為演繹推理之源對典型例題進行剖析，并通過追問和變式的方式，引領學生再發(fā)現(xiàn)、再創(chuàng)造，體悟知識的本質(zhì)，延伸思維和方法，自然建構思想方法結構;通過小結交流，引導學生表達自己的學習感受，深化方法內(nèi)涵，豐富情感體驗，發(fā)展能力素養(yǎng)，體現(xiàn)教學立意。

四、后繼研究展望

從李庾南老師“學材再建構”開始，“單元教學”逐漸進入了研究者的視野。筆者認為章、單元、節(jié)都是用于“分段敘事”的“敘事”段群，它們共同構成了教材編寫的三級結構。一章可以劃分為若干單元，一個單元由若干節(jié)組成，有必要分別從“前建構”“中建構”“后建構”的視角研究章首課、章中課和章尾課的設計。

專題復習作為一類復習課，旨在構建同類異形問題的解決通法，是一種“后建構”;“綜合與實踐”注重數(shù)學與生活實際、數(shù)學與其他學科、數(shù)學內(nèi)部知識之間的聯(lián)系和綜合應用，也是一種“后建構”。綜合三類課型的特征，筆者認為：后建構課堂是指在后建構主義理論指導下，在新知識教學結束后，幫助學生建構系統(tǒng)知識結構、思想方法結構、能力素養(yǎng)結構的課堂。其內(nèi)涵的發(fā)展也是需要繼續(xù)深入研究的重要方面。

章建躍先生為前建構的章首教學指明了方向：構建“先行組織者”，明確一章主線;突出課時重點，掌握關鍵內(nèi)容;落實知識發(fā)生發(fā)展的過程教學，強化研究方法指導，潛移默化地引導學生學會“數(shù)學地認識問題和解決問題的方法”。本文則為章尾教學提供了一個拋磚引玉的樣例。但是，本課直接進入知識梳理，開始全章復習，沒有設計教學情境。實踐中，沒有情境的復習課，極易成為知識的簡單羅列、題目的盲目堆砌，“悟”的過程太短甚至沒有，“知識”量大但缺乏聯(lián)系性、靈活性、變通性，雜亂的知識堆砌成為解決問題的包袱，后果是學生為了考試不得不學，缺乏獨自面對問題的勇氣和能力。有專家提出后建構課也需要設計教學情境。如果需要，那么什么樣的情境既能凸現(xiàn)全章價值、統(tǒng)領回顧全章，又能自然過渡到知識梳理？這也是需要研究者繼續(xù)深入思考的地方。

本文系2020年江蘇省中小學課程基地與學校文化建設項目“基于融合思維的初中數(shù)學課程基地建設”、江蘇省教育科學“十三五”規(guī)劃重點自籌課題“初中數(shù)學深度學習資源建設的理論與實踐研究”（編號：B—b/2016/02/155）、無錫市教育科學規(guī)劃課題“促進學生思維深度參與的中學數(shù)學課堂教學實踐研究”（課題批準號D/D/2018/002）階段性研究成果。

【參考文獻】

[1]卓斌.善用類比方法 構建整體框架——“分式”單元教學課的特色與亮點[J].初中生世界，2018（12）.

[2]鐘鳴.草根教師對復習課的探索——以有理數(shù)復習為例[J].基礎教育論壇，2015（9）.

[3]周建勛.發(fā)展學生的思維能力是數(shù)學教學的核心任務[J].中學數(shù)學教學參考（中旬），2018（9）.

[4]章建躍.從數(shù)學整體觀看“同底數(shù)冪的乘法”的教學[J].中國數(shù)學教育，2013（7—8）.