注重科學思維 提升核心素養
———2020年7月浙江省物理選考壓軸題鑒賞與拓展

俞國富

(浙江省杭州師范大學附屬中學,浙江 杭州 310030)

2020年7月浙江省物理選考第22題取材于離子診斷測量儀,將物理與生產實踐和科技應用緊密聯系起來,充分體現了物理在生產和科技應用中的重要作用．它考查了牛頓第二定律、圓周運動規律、動量定理等考點,覆蓋面廣,綜合性強,是一個傳統的帶電粒子在電磁場中的運動問題．試題陳題新出,頗有創新意識．筆者通過詳細研究發現本題的設問還可拓展延伸,似乎意猶未盡．現略加以拓展,旨在拋磚引玉,引起各位同行作深入的討論．

1 原題呈現

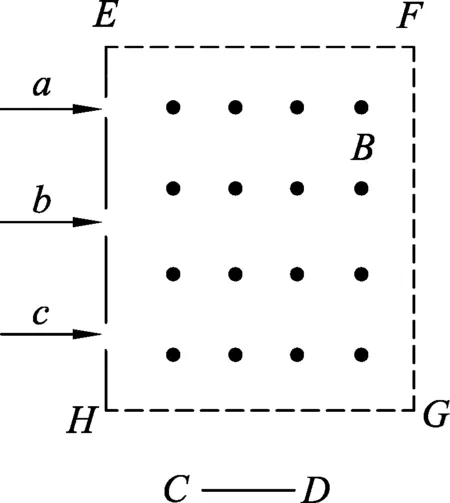
圖1

(1) 求離子速度v的大小及c束中的離子射出磁場邊界HG時與H點的距離s;

(2) 求探測到3束離子時探測板與邊界HG的最大距離Lmax;

(3) 若打到探測板上的離子被全部吸收,求離子束對探測板的平均作用力的豎直分量F與板到HG距離L的關系．

本題是一個傳統的帶電粒子在磁場中的運動問題．本題的一大亮點是磁場中平移圓知識的應用．這一知識考查了學生思維的深刻性,對物理教學中培養學生良好的思維提出了更高的要求,彰顯物理學科核心素養的命題導向,對教師的教學和學生的復習具有引領和指導作用．

2 試題拓展

原題中,左側3束離子束之間的距離為恒定0.6R．筆者認為可以通過調整3束離子束之間的距離,研究能探測到3束離子時探測板與邊界OG的最大距離Lmax,以及對應探測板的最小寬度等方面加以拓展．

假如3束離子束之間寬度d可變,探測板CD的寬度不固定,如圖2所示,L為探測板與磁場下邊界OG之間的距離,d為a、c離子束與中間離子束b之間的距離,α為a、c離子束從OG出射時與豎直方向的夾角,d1為a、c粒子束從磁場下邊界射出時與b粒子束出射點之間的距離．

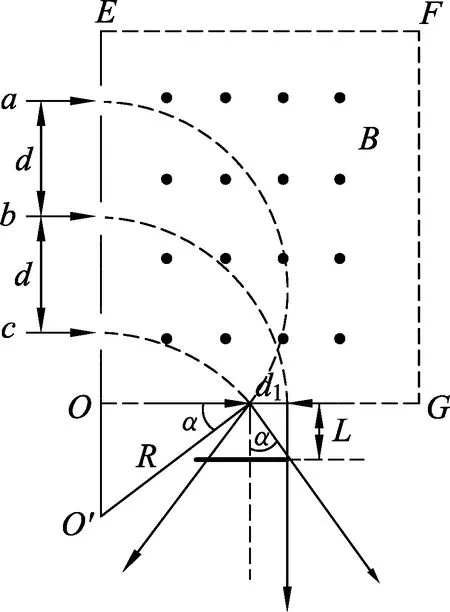
圖2

拓展1: 求探測到3束離子時探測板與邊界OG的最大距離Lmax．

解析： 根據幾何關系可得

(1)

d1=R(1-cosα).

(2)

(3)

由(1)和(2)式得

L=R(1-cosα)cotα.

cosα·(1-cos2α)=1-cosα.

cosα·(1+cosα)=1，

cosα2+cosα-1=0.

(4)

(4)式的根為黃金分割,即當

L取到極大值Lmax．因為cosα2+cosα=1，所以

cosα2=1-cosα.

(5)

(6)

將(5)和(6)式代入(3)式,可得

結論:當d變化,cosα=0.618時,探測板接收到全部離子時,其與磁場下邊界的最大距離為Lmax≈0.300R.

拓展2:當d可調,0

(7)

即d=0.786R時,Lmax=0.300R．

根據(7)式畫圖的結果如圖3所示,對應拓展1,d取0.786R,此時Lmax=0.300R.

圖3

拓展3:當0

(8)

拓展4: 當d可調,0

由幾何關系可得

Dmin=2Lmaxtanα=2(d1cotα)tanα=2d1=

(9)

3 試題啟示

(1) 注重數學知識在物理中的運用．

從本題的分析和拓展可以看出,教學中要重視能夠根據具體問題列出物理量之間的關系式,進行數學推導和求解,并且根據結果得出物理結論;必要時能夠運用幾何圖形、函數圖像進行分析求解．[1]

(2) 注重遷移,強化建模.

高考壓軸題強調理論聯系實際,要求考生把實際情景轉化為物理模型．在平時講解帶電粒子在磁場中運動的臨界問題教學中,我們經常會講解平移圓這種模型方法,本題的求解過程中就要用到這個模型．因此物理教學中要注重知識的聯系,善于注重遷移,運用學過的模型解決新問題.

(3) 注重物理核心素養的滲透與落實.

高考物理壓軸題非常注重科學推理方面的考查．因此在教學中要經常設置一些來源于生活實際,科技應用的問題情境,讓學生運用科學思維探索解決問題,從而讓學生深刻體驗科學思維的愉悅過程,進而提升學生的核心素養．[2]