大學普通力學實驗中驅動頻率對聲速測量結果的影響*

朱旭鵬 廖 峻 薛書文 李佳楠

(嶺南師范學院物理科學與技術學院 廣東 湛江 524048)

聲波是一種能夠傳輸能量的縱波，不同于橫波傳播方向與傳播介質振蕩方向垂直的關系，聲波在傳播過程中，傳播方向與傳播介質的振蕩方向一致，是一種傳播介質的密度疏密波[1]．聲速是用來表征聲波在傳播介質中行進快慢的物理量．理想氣體在熱力學溫度273.15 K時的聲速為331.45 m/s[2]．聲速測量是大學普通物理實驗力學部分中的重要組成部分，是學生綜合理解縱波振蕩、駐波形成和振動合成等物理過程的重要實驗行為．

根據聲波的頻率值可以將聲波分為次聲波(<20 Hz)、可聞聲(20～20 kHz)和超聲波(>20 kHz)．超聲波的傳播速度是理解傳播介質特性或狀態變化的重要物理量[2]．超聲波常見的測量方法有兩種，共振干涉法(駐波法)和相位法(李薩如圖形法)．在大學物理聲速實驗中，通常所采用的聲波頻率為20～60 kHz，這一范圍內壓電陶瓷換能器是超聲波產生和接收的最佳元件[3]．一般地，在聲速測量過程之前需要測定壓電陶瓷換能器的最佳工作頻率點(最強諧振頻率)，以便在后續的測量中獲得高精度的測量值．每對壓電陶瓷換能器都只有一個最強諧振頻率，其測定方法是固定換能器之間的距離，通過調節驅動頻率，找出極大值點對應的頻率即為壓電換能器最強諧振頻率，也是最佳的工作頻率點．但是，我們發現在調節驅動頻率的過程中，不僅僅有一個極大值點，假如每一個極大值點對應一個諧振頻率，那么如果不用最強諧振頻率，而選擇用次強或者次次強諧振頻率，甚至用非諧振的驅動頻率，對聲速測量結果的影響如何，實驗教師和實驗員需要更進一步的把控．

1 儀器 測量原理及頻率選擇

本次實驗探究中所使用的實驗儀器為SV-DH系列聲速測定儀(杭州大華儀器制造有限公司)[3]．其主要構成部分包括綜合聲速測定儀信號源(頻率范圍25～45 kHz)、聲速測定儀測試架(圖1)和示波器3個重要部件．其儀器連接方式如下：

(1)信號源面板上的發射端換能器接口直接與測試架上的發射壓電陶瓷換能器相接；

(2)接收換能器與信號源面板上的接收換能器接口相連；

(3)信號源發射換能器接口和接收換能器接口旁邊的波形接口分別與示波器的信道1和信道2相接．

這樣驅動頻率驅動發射端換能器將電信號轉換成聲波，聲波在接收端接收后被接收端換能器轉換成電信號，再通過示波器呈現出來．信道1接收的發射端換能器的驅動電信號作為參考信號，在相位法測量中扮演重要角色．

如圖1所示，S1作為超聲波發生源，在驅動頻率的作用下發射出水平傳播的平面聲波，S2作為超聲波接收探測器，將部分聲波信號轉換成電信號在示波器中顯示，同時將另一部分反射回S1，所以可以用不同的方式測量S2輸出的信號，從而得到超聲波的聲速[4]．

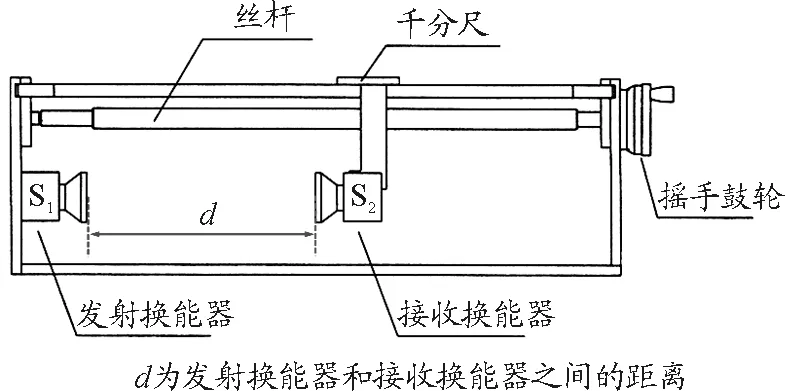
圖1 測試架示意圖

(1)S1發射的和S2反射的兩列聲波在壓電陶瓷換能器之間發生相互干涉，當距離d正好是超聲波半波長的整數倍時，超聲波在換能器之間形成駐波，此時S2接收到的振蕩幅度最大，測出示波器信號極大值對應的位置Li，則相鄰兩個極大值之間的距離d正好為超聲波的半個波長，這一方法記作共振干涉法(駐波法)，也稱為振幅極值法．

(2)將S1和S2對應的波形信號分別輸入示波器的1信道和2信道，并使用X-Y模式比較其相位時，不同的相位差在示波器上呈現不同的形狀．當改變距離d來改變相位差時，示波器上的圖形將經歷橢圓-斜線-橢圓-斜線-橢圓的過程，進一步增大距離時，重復圖形之前的行為．相鄰出現兩次同斜率直線對應的距離差正好是超聲波的一個波長，這一方法記作相位比較法(相位法)，也作李薩如圖形法．

測出超聲波波長λ，再結合信號頻率f，即可通過公式v=fλ獲得超聲波聲速v[5]．

為了更具代表性地選擇驅動頻率點，我們固定壓電陶瓷換能器的距離d=80 mm，對S2對應的示波器信號進行驅動頻率掃描尋找，掃描范圍為29.5 kHz到42 kHz．在掃描過程中，一共發現5個諧振位置，分別位于31.2，33.5，35.5，38.5和40.5 kHz附近，如圖2(a)黑色球體所示．圖2(a)同時定性地給出了S2信號強度隨著頻率的變化趨勢，如黑色虛線所示，整個頻率范圍內存在5個極大值點和4個極小值點．需要注意的是，圖中的強度并不是歸一化的強度趨勢圖，由于諧振強度量級的不同，我們對不同的諧振位置選擇了不同的示波器標度，具體值如表1所示．

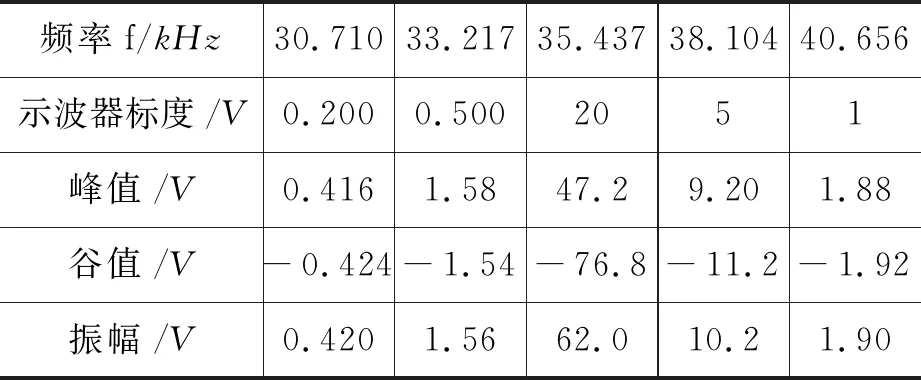
表1 d=80.000 mm時不同諧振峰對應的諧振強度

根據超聲波在空氣中的理論速度計算公式

可以算得在室溫25 ℃的條件下，超聲波的理論速度vs=346.256 m/s．基于此可算得用駐波法和相位法測試過程中，間距的變化范圍在50 mm左右．所以為了能夠在整個距離變化過程中獲得較為精確的測量值，我們以80 mm作為測試起點，分別測試了d=80，100和120 mm時5個諧振峰對應的共振頻率值，如圖2(b)所示，具體數據如表2所示．5個諧振位置分別對應于頻率點1～5，其中3是諧振最強頻率點．如圖2(c)給出了不同頻率點對應的共振率平均值和標準差，這一結果表明只有諧振極強的頻率值對應的標準差最小，而其他諧振頻率點，諧振頻率都會由于距離的變化而發生較大的偏移，這主要是因為接收換能器接收到的聲波強度變弱導致的．需要說明的是，本研究中所有在示波器中讀取的數據都是通過示波器標度和位置旋鈕將圖形優化至最佳讀取的．

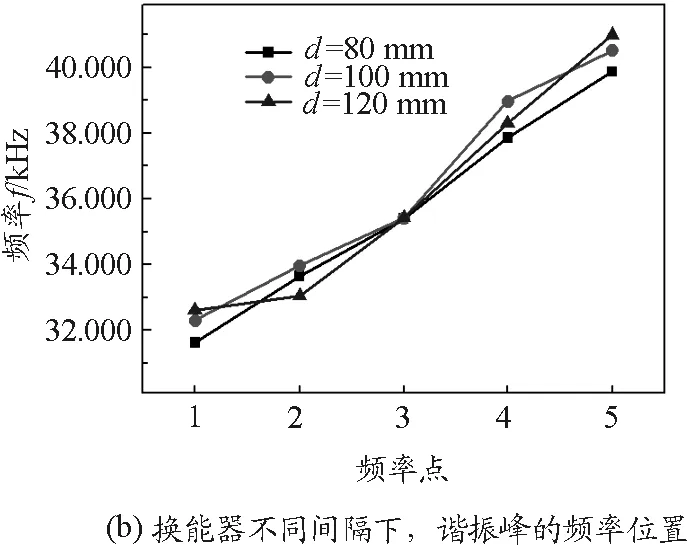
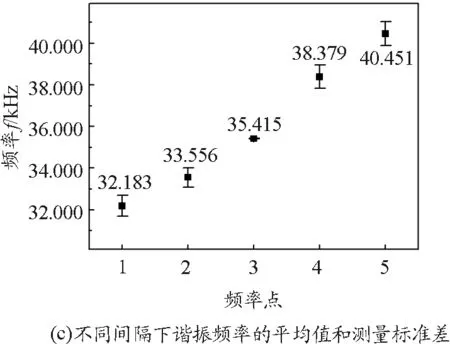
圖2 頻率選擇

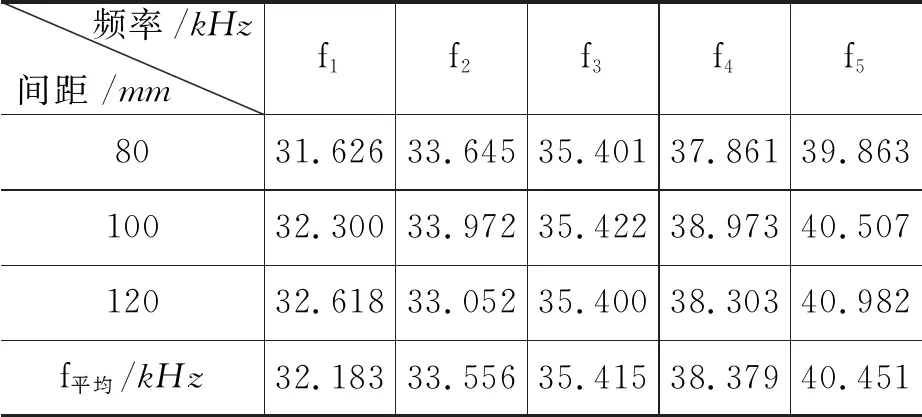
表2 在不同換能器距離下，不同諧振峰

2 結果與討論

依據本文的研究主旨:驅動頻率對超聲波聲速測量的影響，選擇諧振頻率平均值為駐波法和相位法測量超聲波聲速的驅動頻率，其中35.415 kHz為換能器的最強諧振頻率，32.183，33.556，38.378和40.451 kHz為其他次強級諧振頻率．為了系統地研究驅動頻率對聲速測量的影響，我們將33.556 kHz的次強級諧振頻率置換成33.890 kHz的非諧振頻率．具體測量數據如表3所示．

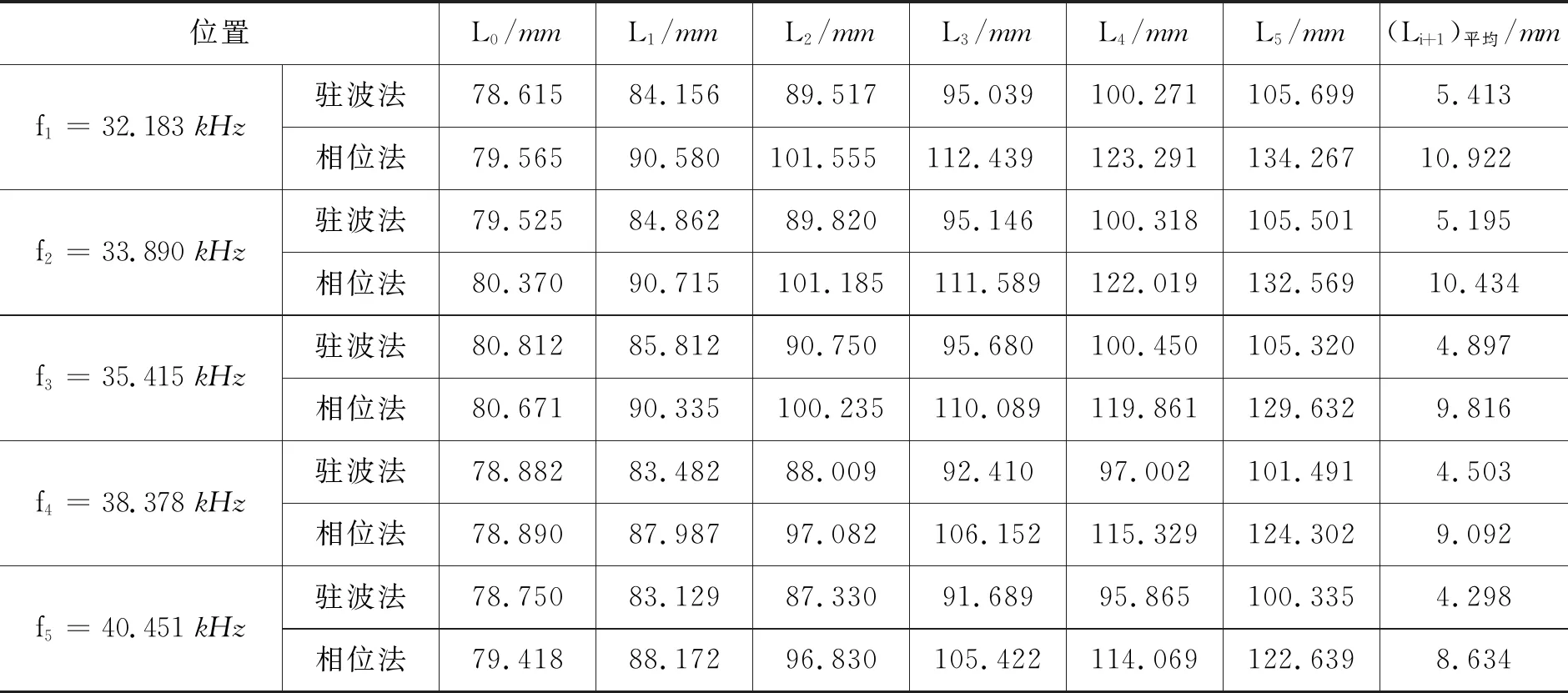
表3 不同頻率點下用不同方法測得接收換能器位置信息

圖3(a)給出了用駐波法測量、用逐差法處理得到的半波長度及其相應的不確定度．結果表明，隨著驅動頻率的增大，所測得半波長的長度近似線性降低，而不確定度呈現起伏變化的趨勢．最強共振頻率處及離其最遠的諧振頻率處測得的不確定度基本持平，而諧振頻率38.378 kHz和非諧振頻率下的測量不確定度相對較低．圖3(b)給出了用相位法測量、用逐差法處理得到的波長長度及其相應的不確定度．數據顯示，隨著驅動頻率的增大，所測得波長也近似線性減小，不確定度先降低，再增大．在諧振最強頻率35.415 kHz和次強級頻率38.378 kHz處的測量不確定度相對較低．綜合來看，除去38.378 kHz處的測量不確定度，相位法測得的波長不確定比相對駐波法更小，也就是相位法具有更高的精度，非諧振頻率處的測量并未展現出更差的精度．

根據波速計算公式v=fλ和誤差傳遞公式，我們分別在圖3(c)和圖3(d)中計算了駐波法和相位法測得的聲速和聲速不確定度．

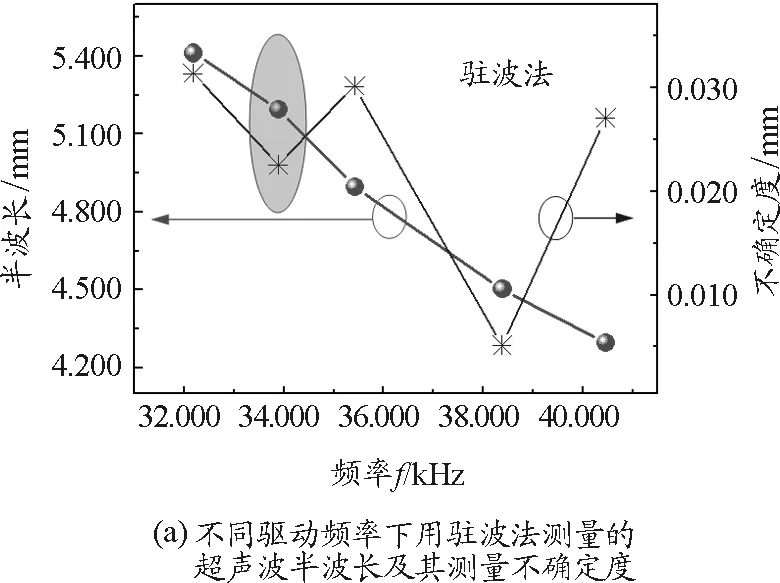
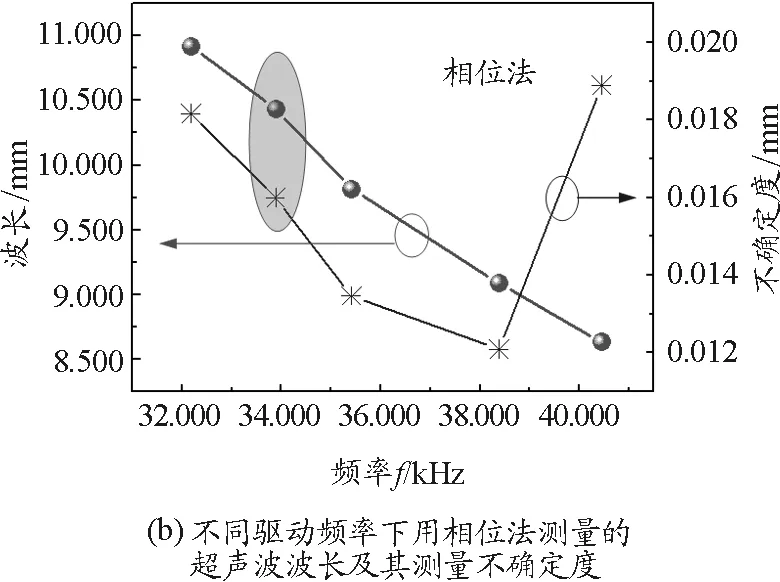
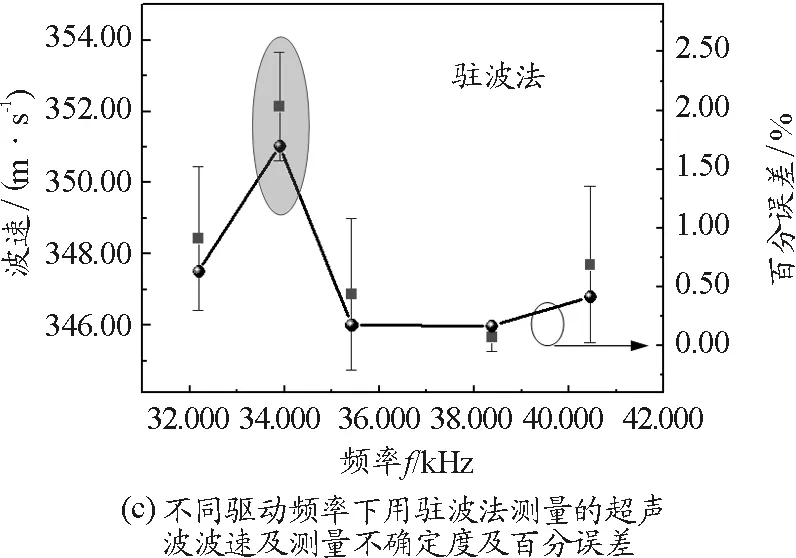
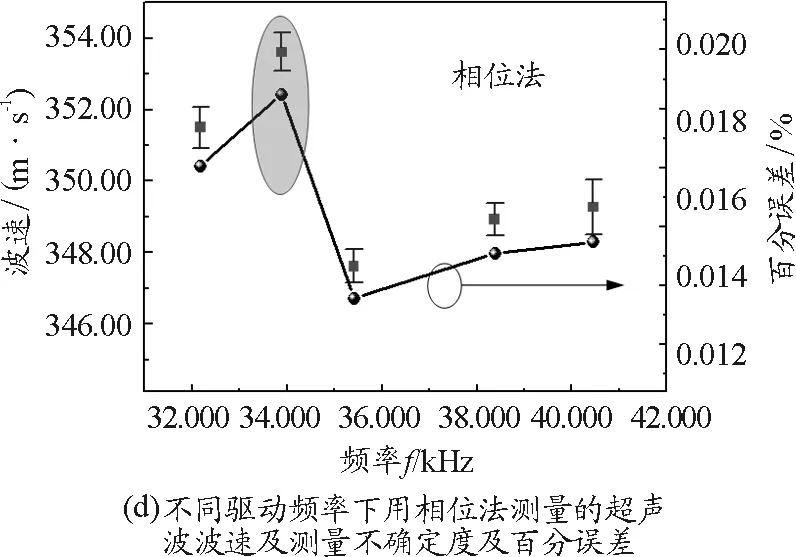
圖3 聲速測量結果

從圖中可以明顯看到，相位法具有更小的不確定度，也就是更高的測量精度．此外在非諧振頻率下測得的聲速相對其他頻率來說稍微偏大，如灰色橢圓位置所示．根據超聲波在空氣中的理論速度346.256 m/s，我們在圖3(c)和圖3(d)中分別添加了不同驅動頻率下測得的聲速百分誤差．

由圖可知在非諧振頻率處測得的聲速百分誤差最大，駐波法和相位法分別可高達1.68%和2.12%．在所有的測試序列中，駐波法和相位法在諧振最強頻率點測得的聲速百分誤差最小．對于駐波法所有諧振頻率下測得的聲速百分誤差都小于0.65%．相位法在所有諧振頻率下測得的聲速百分誤差都小于1.51%，而且當諧振頻率大于等于35.415 kHz，聲速百分誤差都小于0.88%．所以相對而言，駐波法具有更高的準確度．

綜上，壓電換能器在最大諧振頻率下測得的聲速準確度最高，在非諧振頻率下測得的聲速準確度最差，其他次強級諧振頻率離最強諧振頻率越遠，對應的準確度越低．縱覽我們選取的驅動頻率，最大的聲速測量值百分誤差來自于非諧振區，誤差值也僅有2.12%，所有諧振頻率下測得的聲速百分誤差不超過1.51%．而且根據我們的測量數據，相位法具有更高的精度，而駐波法具有更高的準確度．

3 結論

本文對比了在諧振最強頻率、次強級頻率及非諧振頻率下，使用駐波法和相位法對超聲波聲速測量結果的影響．在最大諧振頻率下，聲速的測量結果最為準確；在非諧振頻率下，測量結果準確度最差；離最強諧振頻率越遠，其他次強級諧振頻率下測得的結果準確度越低．相位法的精度更高，駐波法的準確度更高．研究結果表明最大的聲速測量百分誤差來自于非諧振頻率，但誤差值也僅有2.12%，因此在本實驗中，示波器的調節與使用是本實驗的主要誤差來源之一．對于沒有接觸過示波器的學生來說，

實驗教師應該有條理地仔細講解示波器的用法． 我們的研究結果在提高實驗教師把控學生實驗數據、加深測量過程理解和解惑學生問題方面具有一定的指導意義．