基于核心素養建構圓模型圓滿解決力學問題
陳紅林
(曲靖市第二中學 云南 曲靖 655000)
1 建構圓模型解決力學動態平衡問題
1.1 問題概述
三力動態平衡是高中物理中一類重要的平衡問題,對于已知一個力的大小和方向,其他兩個力的夾角,要求其他兩個力的大小變化情況這類問題,我們在畫動態矢量三角形解決時無法保證這兩個力的夾角在動態變化過程中保持恒定,此時我們可以借助圓中同一條弦對應的圓周角相等這一性質在圓中來畫動態矢量三角形.即用已知的一個力為圓的一條弦,對應的圓周角(或者補角)為所求兩個力的夾角,然后在圓中畫動態矢量三角形就可以保證所求兩個力的夾角恒定,這樣此類平衡問題以圓來建模問題就迎刃而解.
1.2 實例應用
【例1】(2017年高考新課標全國卷Ⅰ第21題)如圖1所示,柔軟輕繩ON的一端O固定,其中間某點M拴一重物,用手拉住繩的另一端N,初始時,OM豎直且MN被拉直,OM與MN之間的夾角為α.現將重物向右上方緩慢拉起,并保持夾角α不變.在OM由豎直被拉到水平的過程中( )

圖1 例1題圖
A.MN上的張力逐漸增大
B.MN上的張力先增大后減小
C.OM上的張力逐漸增大
D.OM上的張力先增大后減小
解析:以重物為研究對象,受重力mg,OM繩上拉力F2,MN上拉力F1,由題意知3個力矢量和為零.如圖2建立圓模型,在圓模型中以重力mg為圓的一條固定弦而對應圓周角π-α,F1和F2為其他兩條任意弦在圓中畫矢量三角形,這樣無論F1和F2如何變化都能保證其夾角α不變,通過圓中的動態矢量三角形就可以簡單直觀地得出在F2轉至水平的過程中,MN上的張力F1逐漸增大,OM上的張力F2先增大后減小,所以選項A,D正確;選項B,C錯誤.

圖2 建立圓模型
【擴展應用】如圖3所示,a和b兩細繩一端系著質量為m的小球,另一端系在豎直放置的圓環上,開始時繩b水平.設細繩a和b對小球作用力的大小分別為Fa和Fb.現將圓環在豎直平面內逆時針緩慢地向左滾動90°,則求在此過程中Fa,Fb的大小變化情況.

圖3 擴展應用題圖
通過上述建立圓模型畫矢量三角形不難得出Fa減小;Fb先增大后減小.那如果a和b兩細繩互相垂直其結果又如何呢?這樣一題多變可以幫助學生對建構圓模型解決力學動態平衡問題有更深入的探究和理解.
2 建構圓模型解決動力學問題
2.1 “等時圓”模型概述


圖4 等時圓模型
2.2 “等時球面”模型概述


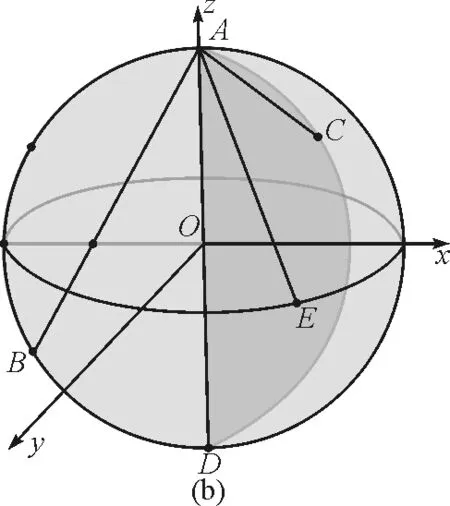
圖5 等時球面模型
2.3 實例應用
【例2】如圖6所示,AB是一傾角為θ的輸送帶,P處為原料輸入口,為避免粉塵飛揚,在P與AB輸送帶間建立一管道(假設光滑),使原料從P處以最短的時間到達輸送帶上,則管道與豎直方向的夾角應為多大?

圖6 例2題圖


圖7 對例2建立等時圓模型
【例3】如圖8所示,圓柱體的倉庫內有3塊長度不同的滑板aO,bO,cO,其下端都固定于底部圓心O,而上端則擱在倉庫側壁,3塊滑板與水平面的夾角依次為30°,45°,60°.若有3個小孩同時從a,b,c處由靜止開始下滑(忽略阻力),則( )

圖8 例3題圖
A.a處小孩最先到O點
B.b處小孩最先到O點
C.c處小孩最先到O點
D.a,c處小孩同時到O點
解析:如圖9所示,我們可以過O點的豎直線為半徑作球面建立“等時球面”模型,可以發現a,c兩點都在半徑為RⅡ的圓周上,故a,c處下滑的小孩同時到O點.而b點在半徑為RⅠ的圓周上并恰好與圓柱體內切,球面半徑RⅠ最小,故從b處下滑的小孩最先到達O點(也是所有圓柱體上下滑到O點的最短時間).綜上所述選項B,D正確.
以上兩個圓模型的建構實例巧妙直觀地解決了動態平衡問題和動力學問題,既突出了高考對學生應用數學處理物理問題能力的考查又培養了學生的科學思維.
因此,在物理實際教學中培養學生的核心素養,是體現物理課程價值的必由之路,教師應該轉變教學觀念,以提升學生核心素養為目標,改善教學的方法和手段,關注學生個體知識的建構和應用.利用典型的物理問題進行科學的分類建模,然后創設問題情境啟發學生去思考與探索,確實以身作則地去培養學生的物理科學思維,以達到提高學生核心素養的目的,意義重大.

