解線性方程組的VRP-GMRES（m）迭代法

白雪婷，楊琴樂

應用科學、物理和工程領域許多問題可建立偏微分方程的數學模型，這些微分方程經過離散后一般都可歸結為求解大型稀疏線性方程組Au=b，A∈Rn×n，u，b∈Rn，其中A為非奇異矩陣.這類方程組的求解通常采用迭代法.目前，以Galerkin 原理為基礎建立的廣義極小殘余GMRES（m）迭代法是求解此類方程組最有效的方法之一.因此，近年來GMRES（m）算法及其在其他領域的應用一直是人們研究的熱點［1-4］.實際計算表明，當系數矩陣A是良態矩陣時，GMRES（m）算法及一些簡單改進后的GMRES（m）算法便可有效地求解這些線性系統［5-6］，但如果系數矩陣A具有很強的病態性，則必須結合一些特定的預處理技術［7-10］.

不管是GMRES（m）算法還是預處理GMRES（m）算法，在實際執行這些算法時，參數m一旦選定，在之后整個迭代過程當中將始終固定不變.所以參數m的選擇也是影響算法有效執行的關鍵因素之一.研究表明，m取值較小時，有可能出現收斂慢甚至不收斂等現象，m選擇過大會造成存儲空間過多的需求.因此，如何選擇一個合適的參數m一直困擾著眾多學者，最近有不少學者試圖通過變化GMRES（m）算法中的重啟動參數m來克服這些困難.BAKE A H 最初通過選擇隨機的參數m來改善GMRES（m）算法的收斂性，后來又根據兩次迭代所得殘余向量的范數之比來確定參數m的大小，但這也并不能保證算法的收斂性［11-12］，PEAIRS L 等則通過強化學習方法來決定參數m的取值，該方法進一步表明適當的參數m可以提高GMRES（m）算法的計算效率，但由于強化學習只是一種機器學習方法，因此存在一定局限性［13］.

1 GMRES（m）算法基本理論

1.1 Galerkin 原理

任意給定向量u0∈Rn，令u=u0+z，則方程組Au=b等價于

其中：r0=b-Au0是初始殘余向量.給定一個參數m＞0，設Rn中兩個m維子空間Km和Lm分別為：

且v1,v2,…,vm和w1,w2,…,wm分別為子空間Km和Lm的基.令求解式（1）的Galerkin 原理為：給定一個m＞0，尋找近似解zm=Vmym∈Km，使(r0-Azm)⊥Lm，即(r0-AVmym)⊥Lm，該 式 也 可 表 示 為(r0-AVmym,ωi)= 0,ym∈Rm.

1.2 Arnoldi 過程及其性質

Arnoldi 過程具體如下（文中若不作特殊說明，‖ · ‖均表示向量的二范數）：

①對m＞0 和初始向量v0∈Rn.計算v1=r0‖r0‖，其中r0=b-Au0；

②對于k= 1,2,…,m，計算hi,k= (Avk,vi)，要 求

③如果hk+1,k= 0，停止；否則vk+1=

Arnoldi 過程有如下重要性質.

定 理1［14］在Arnoldi 過 程 中，令Vm+1=則如下關系成立.

其中：Hm= (hij)m是上海森伯格矩陣，=(0,0,…,1) ∈Rm且I是一個m+ 1 階單位矩陣.

1.3 GMRES 算法

定理2［15］令A為n×n方陣并假定L=AK，u=u0+z=u0+Vmy，則由Galerkin 原理得到的近似解Zm將使殘余向量‖r0-Az‖在Krylov子空間Km中達到最小，反之亦然，并且有

其中：β= ‖r0‖，e1= ( 1,0,…,0)T∈ Rm+1.‖r0-Az‖2等價于在Rm中極小化

這個定理表明，在Km中極小化殘余向量GMRES（m）算法基本思想就是固定重啟動參數m，通過求解最小二乘問題迭代計算求得zm，使得‖rm‖= ‖r0-Azm‖＜τ，GMRES（m）算法詳細步驟如下：

①給定誤差上界τ＞0，給定一個合適的m(m＜n)，取u0∈Rn，計 算r0=b-Au0以及β= ‖r0‖；

④計 算zm=Vmym.若‖rm‖= ‖r0-Azm‖＜τ，迭代終止；否則，令um=u0+zm，u0=um，轉向步驟②.

在GMRES（m）算法中，并非任意選取m都能使其收斂.事實上，適當地變化m可以有效地改善GMRES（m）的收斂性，且在一定程度上可以避免收斂慢甚至不收斂等現象.

2 VRP-GMRES（m）算法

2.1 VRP-GMRES（m）算法

適當變化重啟動參數m，通過迭代使得殘余向量‖rm‖= ‖r0-Azm‖＜τ，具體過程為：

Step1：選擇一個較小的初始正整數m(m?n)，給定誤差上界τ＞0；

Step3：求解如下最小二乘問題

可得ym，計算近似解zm=Vmym，且令um=u0+zm；

Step4：如 果‖rm‖= ‖r0-Azm‖＜τ，迭 代停止，輸出u=um.否則，轉向Step5；

Step5：令u0=um，m=m+ 1(m≤n)轉至Step2.

實際執行VRP-GMRES（m）算法時，可能出現收斂慢甚至不收斂等現象（雖然這種情況較少發生）.所以，為防止參數m過大而造成存儲空間過多的需求，可以先執行若干次VRP-GMRES（m）算法，待m增加到一定程度且殘量范數減小到某一適當值時，再固定m循環迭代，即執行GMRES（m）算法.

2.2 收斂分析

定義1［15］設

其中：實數c和s滿足，稱Gi為平面旋轉矩陣，也稱為Givens（吉文斯）變換矩陣.

定 理3 在VRP-GMRES（m）算 法 中，令

證明 在VRP-GMRES（m）算法中，令式（5）中Gi∈R(m+1)×(m+1)，

其中：i= 1,2,…,m，經i-1 次Givens 正交變換后對角線及次對角線元素.

令Qm=GmGm-1…G1，對 式（4）中和βe1作正交變換，則可得

其中：Rm是m階可逆上三角方陣.

解Rmy=gm，得ym.此時

當參數m變為m+ 1 時，由Arnoldi 過 程，有

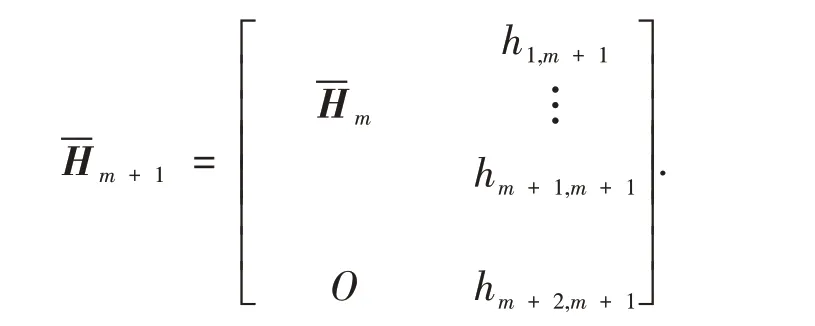
令式（5）中Gi∈R(m+2)×(m+2)，且

其中：i= 1,2,…,m+ 1，取Qm+1=Gm+1Gm…G1，對式（4）中和βe1作正交變換，則

其中：Rm+1是m+ 1 階可逆上三角方陣，

其中：e1= ( 1,0,…,0)T∈ Rm+2,gm+1∈ Rm+1.

于是

解Rm+1y=gm+1，得ym+1.此時

由定理3 知，VRP-GMRES（m）算法不僅收斂，而且比GMRES（m）算法計算精度更高.

3 數值實驗

本節通過兩個不同類型的數值算例說明VRP-GMRES（m）算法的有效性和可行性，分析比較GMRES（m）和VRP-GMRES（m）兩種算法的數值結果.在以下算例中均選取u0=作 為 初 始 向 量，‖rm‖=‖r0-Azm‖＜τ= 1e- 8 作為停止迭代標準.算例1 考慮如下一維波動方程

該方程精確解為：u(x,t)= sin( πx)cos( 2πt)+ sin( 2πx)cos( 4πt)，其中：u(x,t)表示振弦，是對特定位置x和特定時間t的波強度的一個測量，如圖1（a）所示.用中心差分格式離散后可得

其中：n表示x方向和t方向網格數.用VRPGMRES（m）算法求解式（8），計算結果如圖1（b）所示.由圖1 知，式（7）的數值解和精確解是一致的，這也說明VRP-GMRES（m）算法的正確性.

分別用GMRES（m）算法和VRP-GMRES（m）算法求解式（8），當n= 10，m= 7時，cond(A)=56.507 9.GMRES（m）算法循環迭代9 次后出現迭代停滯，此時殘量范數為1.409 9，但對于VRP-GMRES（m）算法，迭代3 次后殘量范數已達到1.423 0e-014.迭代過程各節點絕對誤差大小的比較如圖2 所示.

圖2 迭代過程中各節點絕對誤差大小的比較

由圖2 可知，當迭代次數相同時，用VRPGMRES（m）算法比用GMRES（m）算法得到的計算結果的絕對誤差要小得多，而且隨著迭代次數的增加，用VRP-GMRES（m）算法計算產生的絕對誤差減少得更快.這說明本文算法不僅具有更高的計算精度，而且能快速收斂.

當參數m分別取不同值時，對兩種算法的計算結果進行比較如表1～表4 所示.表1～表4 分別給出兩種算法的迭代次數、運行時間、計算精度和收斂速度比較.從表1～表4 可知，文中提出的算法收斂快，穩定性好，計算精度高，運行時間短.參數m的選擇對GMRES（m）算法至關重要，參數m選擇不當會導致算法失敗，而參數m的選擇對VRP-GMRES（m）算法的執行基本無任何影響.這表明，GMRES（m）算法對參數m的選擇相當敏感，m的微小變化可能會導致GMRES（m）算法出現迭代停滯等現象，而本文提出的VRP-GMRES（m）算法中參數m是變化的，在一定程度上降低了GMRES（m）算法對參數m的敏感度，這也是VRP-GMRES（m）算法的優點之一.

表1 兩種算法迭代次數比較

表2 兩種算法運行時間比較

表3 兩種算法計算精度比較

表4 兩種算法收斂性比較

事實上，當網格數n增大時，系數矩陣A的條件數也不斷增大，當n=59時，A的條件數已達到2.109 8e+003，方程組（8）呈現嚴重的病態性.由表1 知，此時即使參數m取值很大，GMRES（m）算法的收斂速度也不是很快，而且在達到給定誤差時，GMRES（m）算法的迭代次數是VRP-GMRES（m）算法的11.7 倍，運行時間是其10.7 倍.這表明，隨著計算規模地增大，VRP-GMRES（m）算法比GMRES（m）算法更有效，有更廣闊的前景.

算例2 考慮如下二維泊松方程

該方程精確解為u(x,y)=x2(x+y2)+ 2，其中：u(x,y)是溫度分布函數，溫度分布如圖3（a）所示.將式（9）所示的求解區域分別沿x方向和y方向n等分，可得

取n=40，m=10，用VRP-GMRES（m）求解式（10）時，各節點處的溫度分布如圖3（b）所示.由圖3 可知，數值解和精確解是一致的.

圖3 溫度分布（n=40，m=10）

當m=10 時，隨著計算規模不斷增大，VRP-GMRES（m）算法所需迭代次數變化較小且所需的迭代次數要比GMRES（m）少很多，如圖4（a）所示，說明VRP-GMRES（m）算法有更高的計算效率，同時，VRP-GMRES（m）算法還有更高的精度，如圖4（b）所示.另外，實際執行VRP-GMRES（m）算法時，雖然每次迭代所耗時可能比GMRES（m）算法長，但是由于VRP-GMRES（m）算法收斂速度很快，所以當殘量范數達到給定誤差時，如表5 所示，本文提出的VRP-GMRES（m）算法總的運行時間要比GMRES（m）算法少很多.

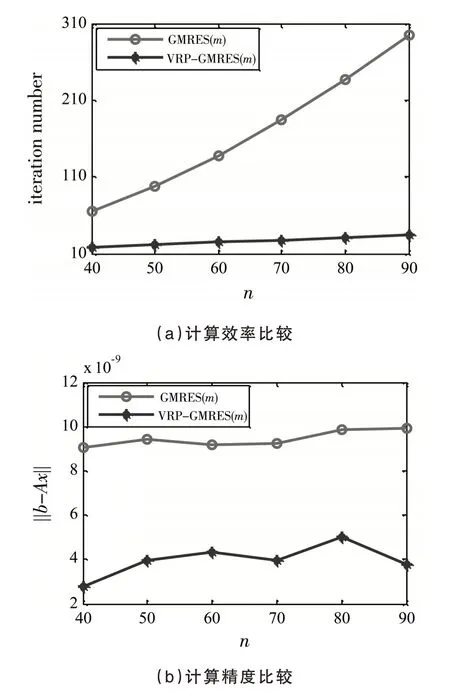
圖4 不同網格下兩種算法計算效率和計算精度比較（m=10）

表5 不同網格下兩種算法運行時間比較

4 結語

文中提出一種求解線性方程組的VRPGMRES（m）算法，理論證明新算法收斂且計算精度更高.數值試驗結果表明本文提出的VRP-GMRES（m）算法不僅有更高的計算效率和計算精度，而且有更好的穩定性.新算法適合用來求解由科學研究和工程問題得到的大型線性方程組.