計及永磁體漏磁效應的磁飽和型高壓直流限流器設計方法

周 航 袁佳歆 陳 凡 張朝陽 胡紅嬌

（1. 武漢大學電氣與自動化學院 武漢 430072 2. 國網湖北省電力有限公司恩施供電公司 恩施 445000）

0 引言

隨著新能源的不斷接入、大功率遠距離電能輸送的迫切需求及現代電力電子技術與全控型功率器件的迅猛發展，直流輸電系統的傳輸容量、電壓等級、跨越距離都有了顯著的提升，高壓直流輸電也成為大容量遠距離輸電的首選方式[1-2]。然而，直流系統阻尼小，導致直流故障電流上升速度快，過電流峰值高，對于保護的快速性要求很高，進而成為威脅系統安全穩定運行的一個巨大隱患。因此，亟需可靠經濟的短路電流限制手段及設備，降低系統運行風險，保障其安全穩定運行[3-7]。

可變電感型限流器利用快速變化的電感值限制故障電流上升速度，是近些年來的熱門研究方向，主要有開關投切[8-11]和磁飽和變化[12-15]兩大類別。磁飽和型直流限流器利用鐵磁材料磁化非線性特性，正常工作時鐵心處于飽和狀態，限流器對直流系統呈現小電感值，不影響系統穩定運行；故障時刻鐵心退出飽和態，限流器對直流系統呈現大電感值，有效增大故障阻尼，大大降低了直流故障電流的上升速度。該方法采用鐵磁材料作為能量傳遞媒介，設備耐受高壓大電流能力強，整體性能及經濟性佳，十分適合高壓直流系統裝設，是直流限流器相關研究的重要分支之一。

為了獲得磁飽和型限流器的主要尺寸及電氣參數，限流器設計計算是必不可少的一個步驟。目前磁飽和型限流器的設計計算方法主要分為如下幾大類別：

（1）經驗公式法：利用傳統變壓器設計公式，通過短路容量確定鐵心邊柱尺寸，電壓確定繞組匝數，進而初步得到基本參數[15-16]。該方法設計速度快，但是精度不高，難以得到準確的尺寸與電氣參數值。

（2）數值迭代法：基于有限元剖分解析[15]或磁鏈-電流公式[18-20]進行循環迭代計算，首先通過經驗公式得到基本幾何參數，然后設置約束條件迭代求解，獲得精確尺寸及電氣參數值。該方法精度高，但是比較耗費計算資源及時間，需要進一步優化算法求解過程。

（3）磁阻網絡法：獲得磁路不同部分的等效磁阻值，建立等效磁阻網絡，求解磁路與電路方程，得到限流器電感及尺寸參數[14,20-21]。該方法研究較為廣泛，精度較高，計算速度快，其難點在于如何確定磁路不同區域的磁阻值，并且現有方法尚未考慮永磁偏磁型直流限流器的漏磁效應，對整體設計影響較大，需要進一步深入研究。

針對上述問題，本文結合上述設計計算方案的優缺點，提出一種基于高階麥克勞林展開的磁通管區段擬合方法，充分考慮永磁體漏磁效應對磁飽和型直流限流器性能產生的影響，計算等效磁路的磁阻網絡，得到計及永磁體漏磁效應的磁飽和型高壓直流限流器設計計算方法，最后利用多組有限元仿真及等效實驗驗證了所述方案的有效性。

1 原理分析

圖1 所示為典型永磁偏磁型高壓直流限流器拓撲及等效電磁路[12]。

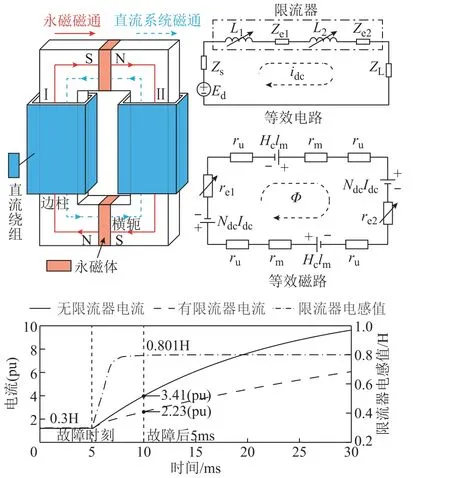
圖1 永磁偏磁型直流限流器拓撲及等效電磁路圖Fig.1 Topology and equivalent circuits of PM biased saturated core FCL in HVDC system

該限流器由鐵心、釹鐵硼永磁體及直流繞組構成，直流繞組串聯進入系統，產生的磁動勢方向與永磁體相反。系統正常工作時電流較小，永磁體產生的磁動勢遠大于直流繞組產生的磁動勢，使得雙柱鐵心飽和，直流繞組對外呈現小電感值，有效替代系統直流側的平波電抗器；故障發生時刻，直流電流陡增，繞組產生的磁動勢抵消大部分永磁體磁動勢，此時雙柱鐵心退飽和，限流器電感值由初始臨界飽和態的低電感值躍變為退飽和態的高電感值，變化時間約為2ms。在到達退飽和態高電感值后，鐵心磁阻re較永磁體磁阻rm而言小很多，因此鐵心持續退飽和時電感值維持不變，對外會持續呈現大電感的限流效果，如圖1 所示。故障電流上升速度會顯著降低，故障電流瞬時峰值也會較沒有限流器時降低，此時故障電流產生的反向磁通增加速度也會降低。此外，鐵心硅鋼片臨界飽和磁感應強度約為1.9T，達到反向飽和所需故障電流反向磁動勢較大，鐵心不會在短時間內進入反向飽和階段。

考慮到目前直流系統配備的直流斷路器動作時間在10ms 以內，由圖1 所示的限流器故障態大電感持續時間大于20ms，鐵心在此階段始終未進入反向飽和狀態。所述限流器與斷路器配合工作，故障電流上升速度將顯著放緩，斷路器可以在故障初期5～10ms 內有效切斷故障電流。因此，所述限流器在工作過程中不會因反向飽和而失去限流能力。

求解限流器等效電磁路，得到方程為

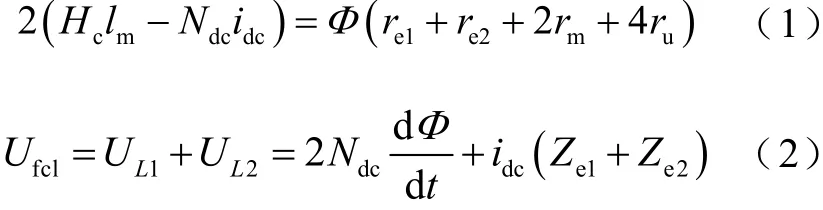
式中，Ndc為直流繞組的匝數；Φ為鐵心磁通；re、ru和rm分別為邊柱、鐵軛和永磁體的磁阻，可以通過r=l/(μS)描述，其中l為磁體長度、μ為磁體磁導率、S是磁體截面積；Ufcl為限流器電壓；UL1、UL2為左、右繞組電壓。

由圖10 可得，永磁體中心附近空氣漏磁效應較左右兩側邊軛附近空氣而言明顯許多，且隨著故障的發生，漏磁效應較正常工作時更為明顯，空氣處最大漏磁場強度增長了近2 倍。由此可見，在限流器工作過程中，漏磁效應是一個不可忽視的因素，需要在設計計算過程中加以考慮。

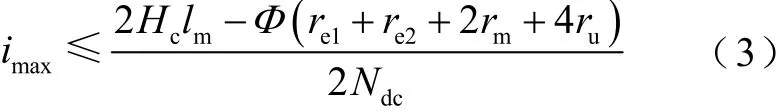
計算機網絡的安全問題關系到企業的隱私，一直以來是企業經營管理者所困擾的問題，其主要包括：電腦病毒、網絡黑客、網站漏洞等。不法分子利用企業的漏洞進行攻擊，盜竊機密文件，嚴重威脅到企業信息的安全，給企業帶來巨大損失。此外，技術人員技能和電腦軟硬件設施的不足也會導致一系列安全問題，給了不法分子可乘之機，影響企業網站的正常運營。

根據法拉第電磁感應定律及磁通連續性定律方程可得

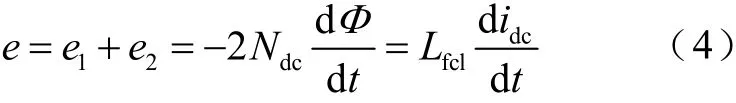
將式（1）對時間t求導可得

將式（5）代入式（4），可以求得限流器等效電感值為

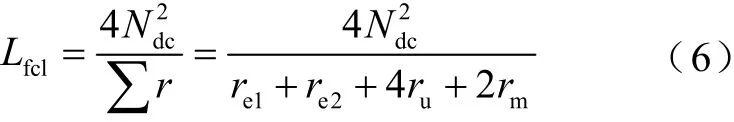
不同于鐵心深度飽和的磁飽和型交流限流器，永磁偏磁型高壓直流限流器為了在正常工作時有一定電感值，雙柱往往為臨界飽和（非深度飽和），鐵心存在一定磁導率。此時式（6）中兩柱磁阻re1+re2不會很大，而磁回路中永磁體磁阻2rm將占總磁阻∑r的較大部分，導致限流器工作電感值將在極大程度上取決于永磁體磁阻。現有計算方式往往將永磁體當作空氣氣隙計算其磁阻，未考慮其邊緣漏磁效應，導致計算磁阻值偏高，與實際情況不符，因此需要進一步分析其漏磁特性，得到精確的設計計算方案。

2 磁通管區段擬合方法

為了解決上述設計計算不準確的問題，本文提出了一種基于漏磁磁通管區段擬合的方式，有效計及永磁體漏磁效應，重構磁阻網絡，獲得準確設計的計算值。限流器磁通管區段擬合方法如圖2 所示。

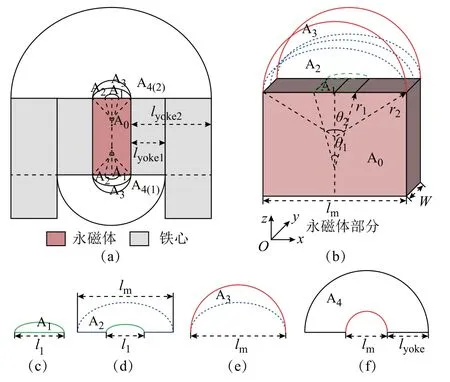
圖2 磁通管區段擬合方式Fig.2 Configuration of the segment fitting strategy of the magnetic flux tube

根據磁通管計算原理，不同部分的磁導G計算公式為

對供試品溶液穩定性進行了考察，結果表明，供試品溶液在24 h內穩定。對不同薄層板（青島鼎盛高效硅膠G薄層板、青島海洋硅膠G薄層板）比較，結果表明，試驗用的薄層色譜條件重現性好，層析的結果穩定。

式中，0μ為空氣磁導率，0μ=4π×10?7H/m；V為所計算磁通管的體積；Lp為該磁通管的等效長度。式（7）是磁導計算的通用公式，將不同磁通管部分的尺寸參數代入此式，即可得到所需部分的磁導值，進一步得到磁阻網絡，計算結果準確可靠。

圖2 中，l1、lm、lyoke1和lyoke2是不同磁通管部分的邊界長度，θ1和θ2是A2磁通管部分的邊界圓心角度，r1和r2是其半徑大小，W是模型的厚度。利用磁通管分段方式，將永磁體漏磁區域分為A1～A4共4 個不同部分計算，分別如圖2c～圖2f 所示。根據這4 個部分的不同幾何特征，采用上述磁通管計算式（7），確定其磁導計算方式，得到準確的限流器磁導矩陣。具體求解方案如下。

2.1 拱形磁通管A1

圖3 所示為典型新月形磁通管計算模型圖。由于圖2 所示拱形磁通管A1與新月形磁通管A3部分的計算模型均可以此為基礎，計算出此新月形磁通管通用模型后，改變不同的邊界條件，代入通用模型公式即可得到A1與A3的磁導值。

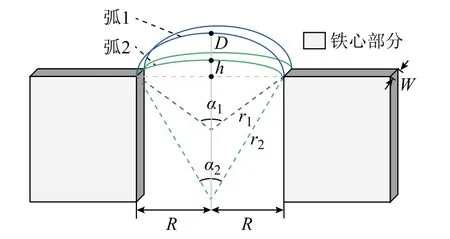
圖3 典型新月形磁通管計算模型Fig. 3 Typical flux distribution of crescent moon shape magnetic flux tube

圖3 中，弧1、弧2 分別為新月形磁通管的上、下邊界，其圓心在共同中軸線上。兩弧共一弦，弦長為2R，半徑分別為r1、r2，圓心角分別為α1、α2。由圖3 可以看出，式（7）中的Lp是弧1 與弧2 間的任意一條弧長，因此Lp可以計算為

式（7）中的體積微元dV可以由式（9）計算得到。

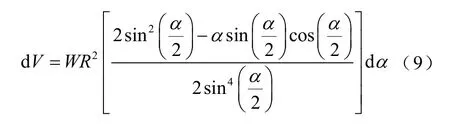
因此，將式（8）與式（9）代入式（7），可得該類磁通管磁導的計算式

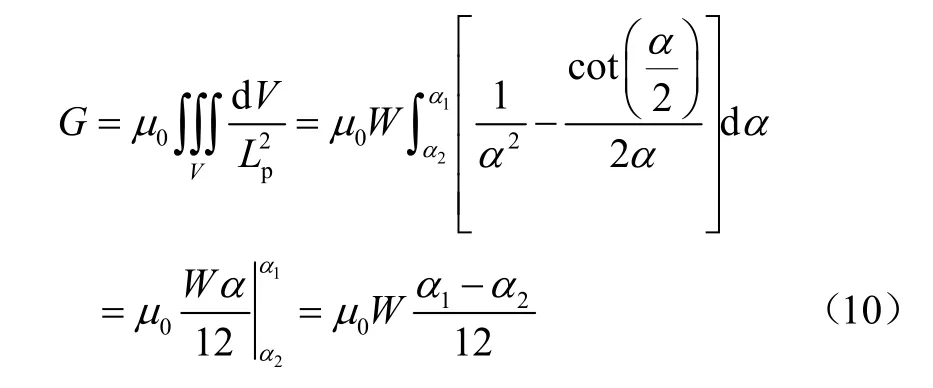
對于拱形磁通管A1，將其邊界條件α1=θ1，α2=0代入，可得其磁導為

2.2 半環形磁通管A2

磁通管A2形狀類似于半環形，如圖2b 所示。按弦長方向進行磁通管積分，可以得到A2部分的磁導值GA2為

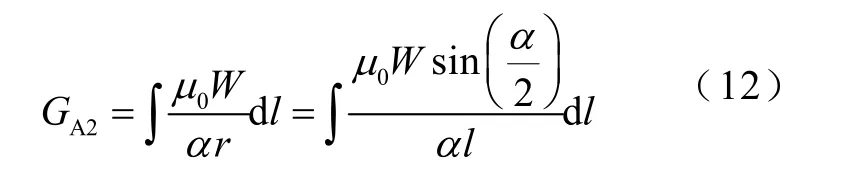
式中，l為邊界弧的半徑r在x軸上的投影長度，即弦長的一半，其范圍在0.5l1～0.5lm之間，如圖2d 和圖2e 所示。由于式（12）中的項無法用α的初等函數簡化表示，因此采用高階麥克勞林展開方式，將展開可得

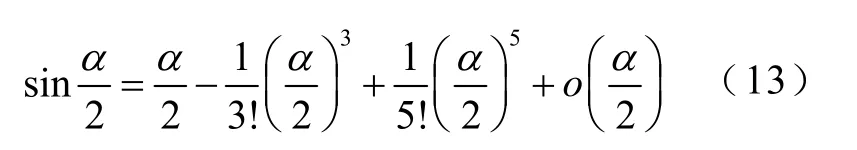
式中，o(α/2)為高階無窮小項。

此外，由于圖2 中α與l的關系較為復雜，無法通過數學模型計算得到。因此本文采用Maxwell 仿真與Simulink 擬合結合的方式，首先搭建圖2b 所示典型永磁體漏磁模型，有限元仿真得到A2區域的漏磁磁力線分布云圖，確定磁力線對應圓弧的半徑、圓心角及半弦長，結合Simulink 曲線擬合工具箱，得到α與l的關系。A2部分參數Simulink 擬合結果如圖4 所示。

圖4 A2 部分參數Simulink 曲線擬合結果Fig.4 Curve fitting results of the A2 part

由圖4 可知，A2部分漏磁磁力線等效圓心角α與對應半弦長l近似為線性關系，因此用式（14）描述其函數關系。

式中，m=531、n=0.093 5。將式（13）、式（14）代入式（12），可得GA2磁導值為

2.3 新月形磁通管A3

如圖3 所示，新月型磁通管A3也是其計算模型的一種特殊情況。因此，將此新月形的邊界條件，即α1=π、α2=θ2代入式（11），可以得到此新月形磁通管A3的磁導值GA3為

2.4 拱橋形磁通管A4

因此，最終可得準確限流電感計算值為

4）制定嚴密有效的合同條款。在簽訂施工合同時，建設單位應做好事前把關，主動監控，通過合同管理形式強化對工程質量的管理，要求施工企業在開工前制定質量保證體系，并將相關責任人進行備案。凡工程中出現質量問題，除按規定整改外，對產生后果和影響的責任方給予一定的經濟處罰。對質量問題的發現者給予物質獎勵。

首先，在機械設備購置之前，需要做好相關的調查工作，按照地質勘察施工的實際情況以及工程項目的整體內容做好核算，保證選擇的設備型號能夠符合工程實際。

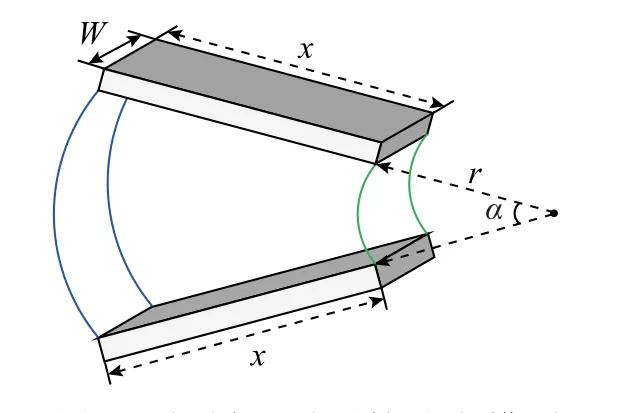
圖5 拱橋形磁通管分布模型Fig.5 Typical flux distribution of arch bridge shape magnetic flux tube

由圖5 可知，式（7）中的磁通管等效長度pL以及體積微元dV均可以由r、x、α表示為

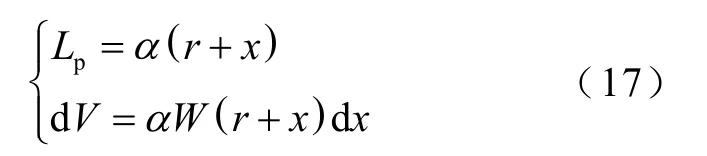
因此，將式（17）代入式（7），可得到圖5 所示拱橋形磁通管的通用磁導值計算公式為

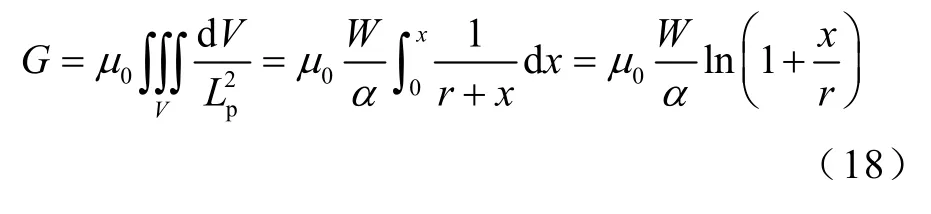
由圖2f 可知，拱橋形磁通管A4的邊界條件為x=lyoke、r=lm/2、α=π，將其代入（18）中可得拱橋形磁通管A4的磁導GA4為

好幾次，蔣春豬想跳下來，可馬跑得太快，他跳下來，不死也得重傷，他又是呼喝又是扯韁繩，藍晶馬終于停了下來。蔣春豬撥轉馬頭就往回跑。

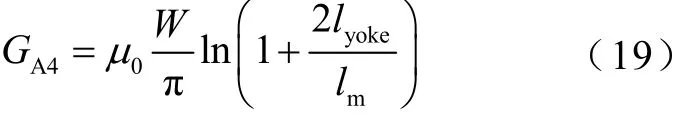
由于鐵心結構原因，永磁體上下漏磁范圍不同，此拱橋形磁通管也存在兩個不同上界，即圖2a 所示lyoke1和lyoke2。將二者代入式（19），可得上下漏磁磁導GA4(1)和GA4(2)。

2.5 重構限流器磁阻網絡

通過對上述不同部分磁導值GA1～GA4的模型建構及計算，可以得到計及永磁體漏磁效應的限流器準確磁導值，將其代入圖1 所示等效磁路中，可以得到考慮漏磁磁導的限流器等效磁路網絡，如圖6所示。其中磁導G與磁阻r的關系為

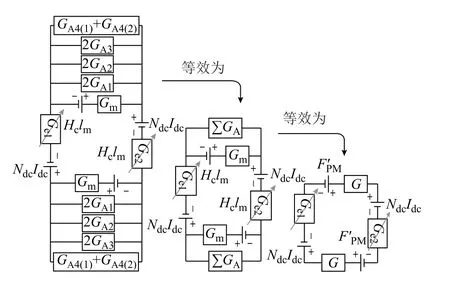
圖6 等效磁導網絡及簡化流程Fig.6 Equivalent magnetic circuit with leakage effect and simplification steps

相較圖1 所示原始磁路，考慮漏磁效應的磁導網絡將GA1～GA4并聯進永磁體磁導Gm支路上，化簡可得最終等效磁導G以及等效磁動勢FPM′ 為

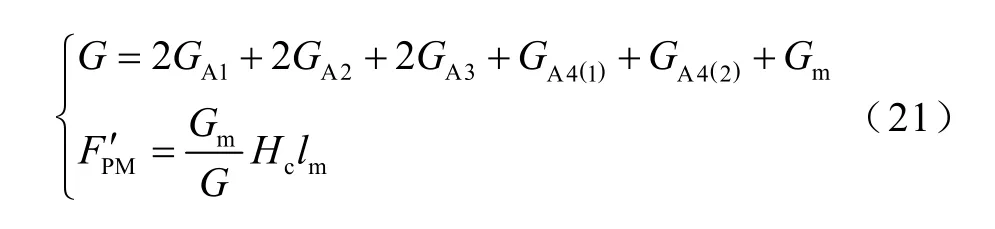
作為最外層磁通管，拱橋形A4的內外邊界均為共圓心的半圓環，其計算模型如圖5 所示。圖中α為兩邊界磁力線的圓心角，r為內部邊界的半徑，r+x為外部邊界的半徑。

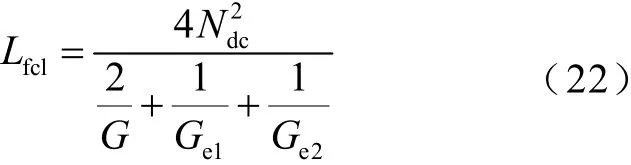
通過上述計算公式，可以得知這些磁導值僅取決于不同部分的尺寸參數與計算公式，與半徑、圓心、匝數等間接計算參數解耦，因此計算精度及可靠性可以保證。

3 設計計算方案

依據上述計算方法，可以構建永磁偏磁型直流限流器以及相關電力設備（包括永磁預偏磁型功率電感、永磁型特種變壓器等）的設計理論依據。設計流程如圖7 所示。

為了簡化設計流程，采取如下兩個假設[22]：①所用磁性材料的磁化曲線為小斜面模型，如圖8a 所示；②鐵心的邊柱截面積為正方形，厚度寬度均為W，其余尺寸如圖8b 所示。

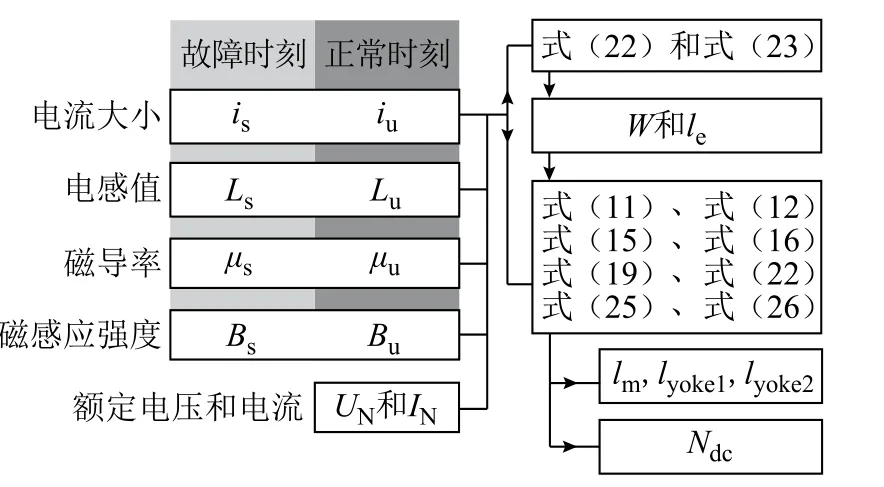
圖7 永磁偏置型設備的設計流程Fig.7 Design flow chart of the PM biased facilities

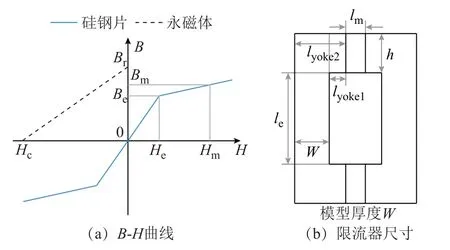
圖8 模型設計參數Fig.8 Parameters of the design model

由圖 8a 可知，μm=Br/Hc、μu=Be/He、μs=(Bm-Be)/(Hm-He)，其中μm、μu、μs是永磁體、非飽和態鐵心及飽和態鐵心的磁導率。由圖8b 可知，鐵軛尺寸存在等式關系，即

③山洪溝治理工程與中小河流治理和水土保持工程既有區別又有聯系。山洪溝治理工程除了采用中小河流治理的工程措施之外，還應重視消能與防沖，重視河床固定與平穩水流，有目的地攔擋從上游向下游流動的巨石和林木。山洪溝治理與水土保持工程緊密聯系，水土保持工程中常用的工程措施在山洪溝治理工程中有所應用，但山洪溝治理工程重在重要河段防洪標準和防沖能力的提高，重點不在整個小流域水土保持的綜合治理。

根據變壓器設計原則，得到鐵心柱截面積計算式為

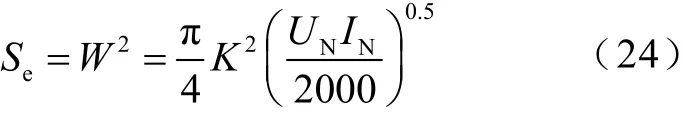
式中，K為硅鋼片系數，一般取5～6。將限流器飽和態電感值Ls與非飽和態電感值Lu代入式（22），可得磁阻間的等式關系，并依此求得鐵心柱長度le的值。

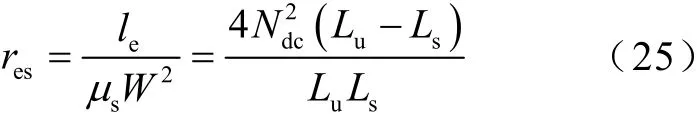
此外，根據限流器磁路電路耦合方程，可以得到磁通、磁導、磁感應強度、電流、匝數、尺寸間的關系式為

因此,緊急制動曲線可以通過上述原則進行計算。ATP系統在列車運行過程中將實時對列車的能量進行檢測，確保在最壞的情況下后車也不會越過前車的干擾點。

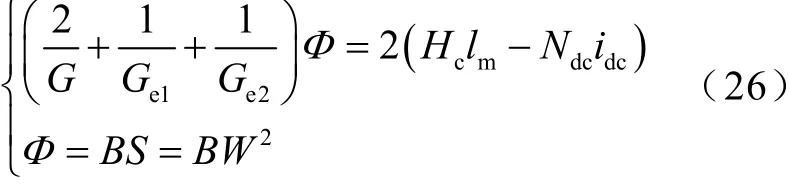
綜上所述，首先根據式（23）～式（25）求得尺寸W、le值，然后將正常及故障態的電流、磁感應強度等已知量代入式（11）、式（15）、式（16）、式（19）～式（22）、式（26），可以求得未知的lyoke1、lyoke2、lm、Ndc值，進一步得到限流器全尺寸參數。對于永磁偏磁型電感設備，改變設備電壓、電流、電感值、磁感應強度、磁導率、鐵心參數等條件，可計算得到相應尺寸參數。

若設備磁結構發生變化，不再是兩柱型永磁體中央鑲嵌式結構，則本文方法需要進一步完善以適應結構變化。此時可將永磁及鄰近鐵心部分單獨分塊，各個分塊形成一個類似圖8b 鐵軛部分的獨立對稱結構，再對各個模塊進行磁導計算，最后通過對本體磁阻網絡的分析，代入相應部分磁導值便可以計算得到裝備的電感值。在已知電氣及結構框架的前提下，也可以利用已知條件反推計算得到設備的具體尺寸參數。

4 仿真分析

為了驗證上述方案的有效性，搭建了多組Ansoft 仿真模型，采用不同尺寸參數值及電壓電流等級驗證所述方案的有效性。仿真模型采用渦流場自適應剖分方法得到精密的剖分網格，導入瞬態場模型開展仿真分析，并采取0.1ms 計算步長，盡可能精細化求解有限元模型，使得其求解結果近似為實際準確值，盡可能減小有限元建模及計算帶來的誤差。同時，后續第5 節也開展了所述兩柱式限流器的樣機實驗，將仿真、實驗、計算所得結果均進行了對照，驗證本文所述方法的正確性。

仿真平臺為裝備i7-8700k CPU、16GB RAM 的計算機，模型參數見表1。其中案例1～3 為小功率模型，改變不同永磁體及鐵心尺寸驗證所述方案有效性；案例4 為高壓大功率模型，驗證所述方案在HVDC 系統中的適用性；案例5 為三柱式鐵心結構模型[14]，驗證本方案在不同磁結構下的有效性。對照分析將Ansoft 仿真作為準確解，以式（6）為代表的不考慮永磁漏磁效應的磁阻網絡法作為傳統方法對照組，驗證本文新計算方法的有效性。

對于上述研究模型，存在如下給定的工作狀態：圓心角θ1=32°=0.558 5(arc)、θ2=83°=1.448 6(arc)，磁感應強度Bs=1.87T、Bu=1.3T，剩磁Br=1.425T，磁導率μs=30μ0、μu=7 000μ0、μm=1.163μ0，矯頑力Hc=975 000A/m，基礎電感值L0=300mH。

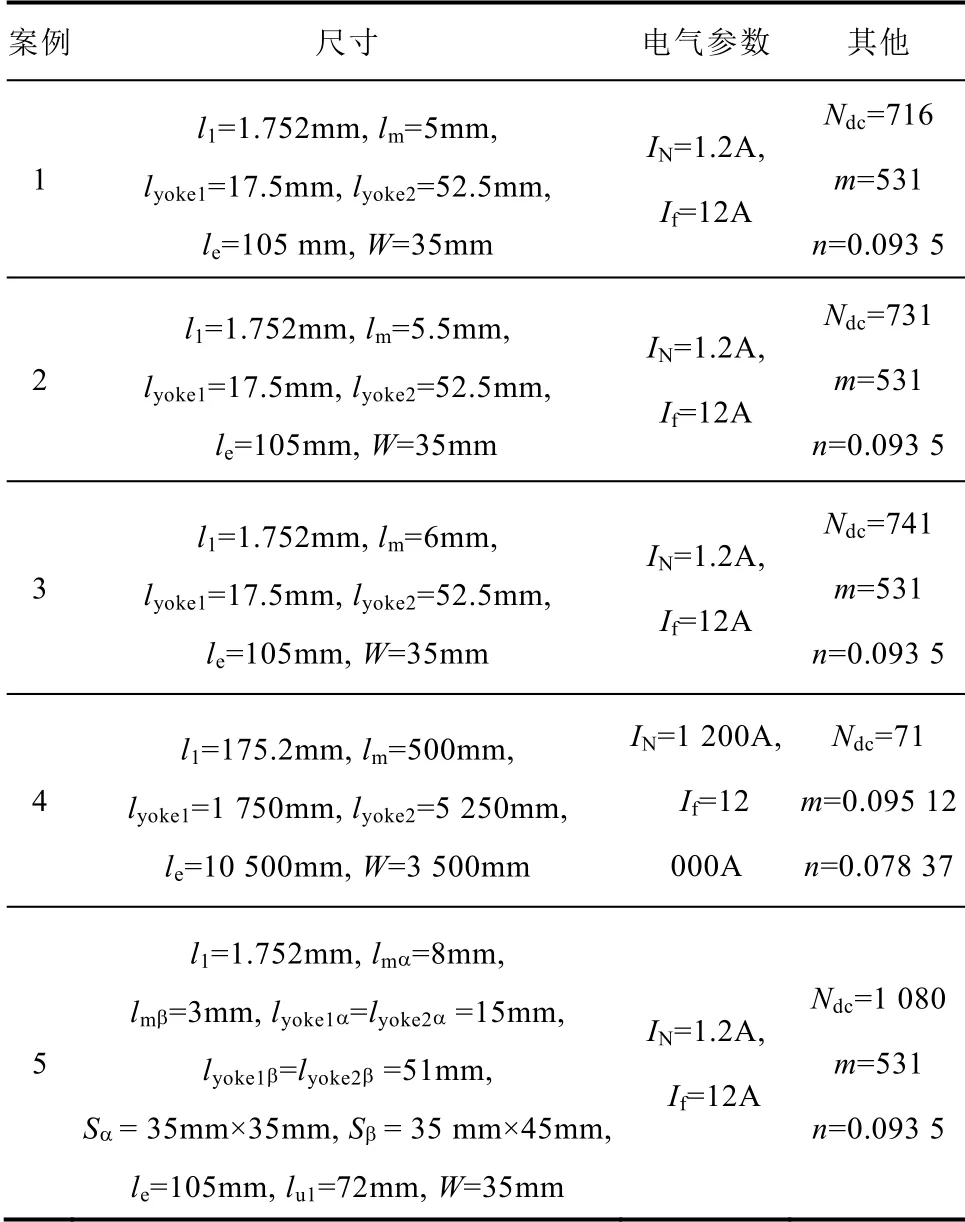
表1 仿真模型參數Tab.1 Parameters of the simulation models

圖12 所示為實驗平臺及等效電路。實驗利用三相電壓源配合三相不可控整流橋輸出直流電流，通過投切電阻的方式模擬系統末端故障，正常工作時R1與R2均串入系統，故障發生時切掉大負載R1，模擬電流陡增效果。

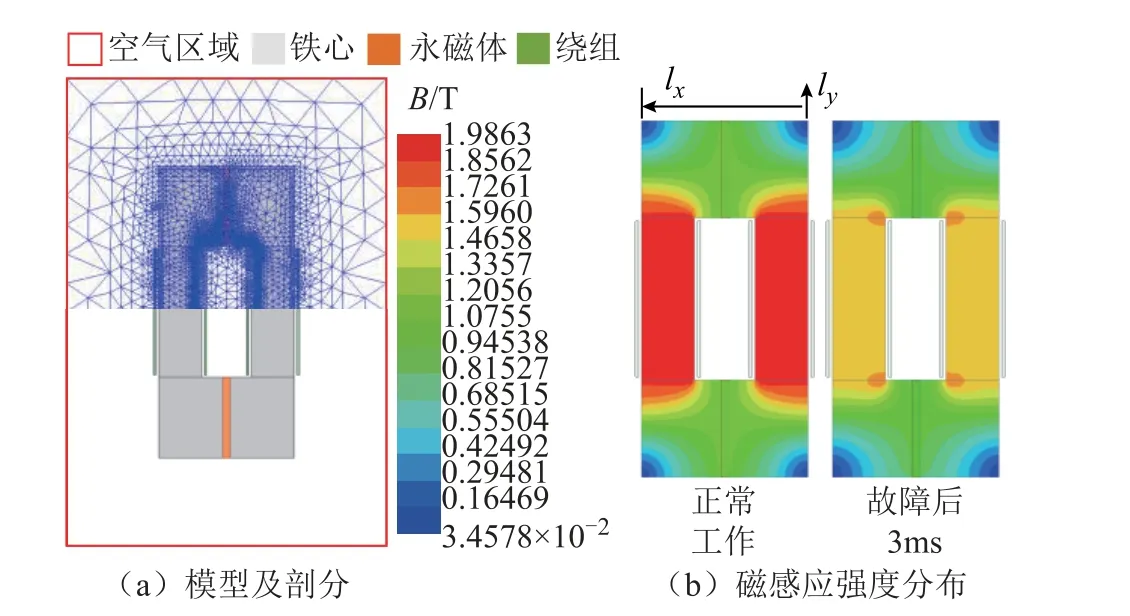
圖9 模型及剖分仿真結果（案例）Fig.9 Simulation results (Case 1 for example)

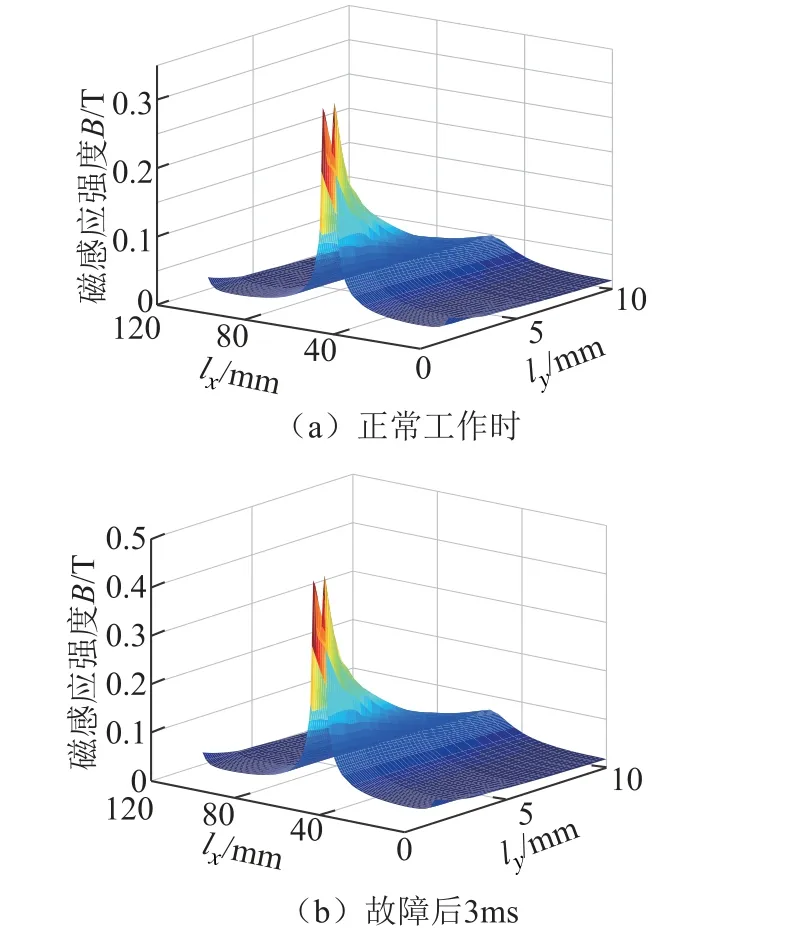
圖10 永磁體附近漏磁分布Fig.10 Flux density distribution of the vicinity of the magnet in the air

確定系統故障電流的變化范圍，采用最大故障情況設計限流器尺寸參數并滿足式（3），確定邊柱鐵心截面積等尺寸防止磁通過快反向。

表2 所示為計算及仿真的對比情況。采用精確剖分的有限元仿真作為準確解，對比所述方法與不考慮漏磁效應傳統方法的計算電感值，驗證所述方法的準確性。傳統方法由于不考慮永磁體上方漏磁效應，導致總磁阻偏高，因此計算電感值相較實際值偏低，存在20%左右的計算誤差。相較傳統方法而言，所述新方法考慮漏磁磁阻并重構磁阻網絡，得到較為精確的計算電感值，不同模型的計算結果與有限元仿真的誤差均在1.3%以內，驗證了所述方法在不同場合下均有較好的精度與計算可靠性。

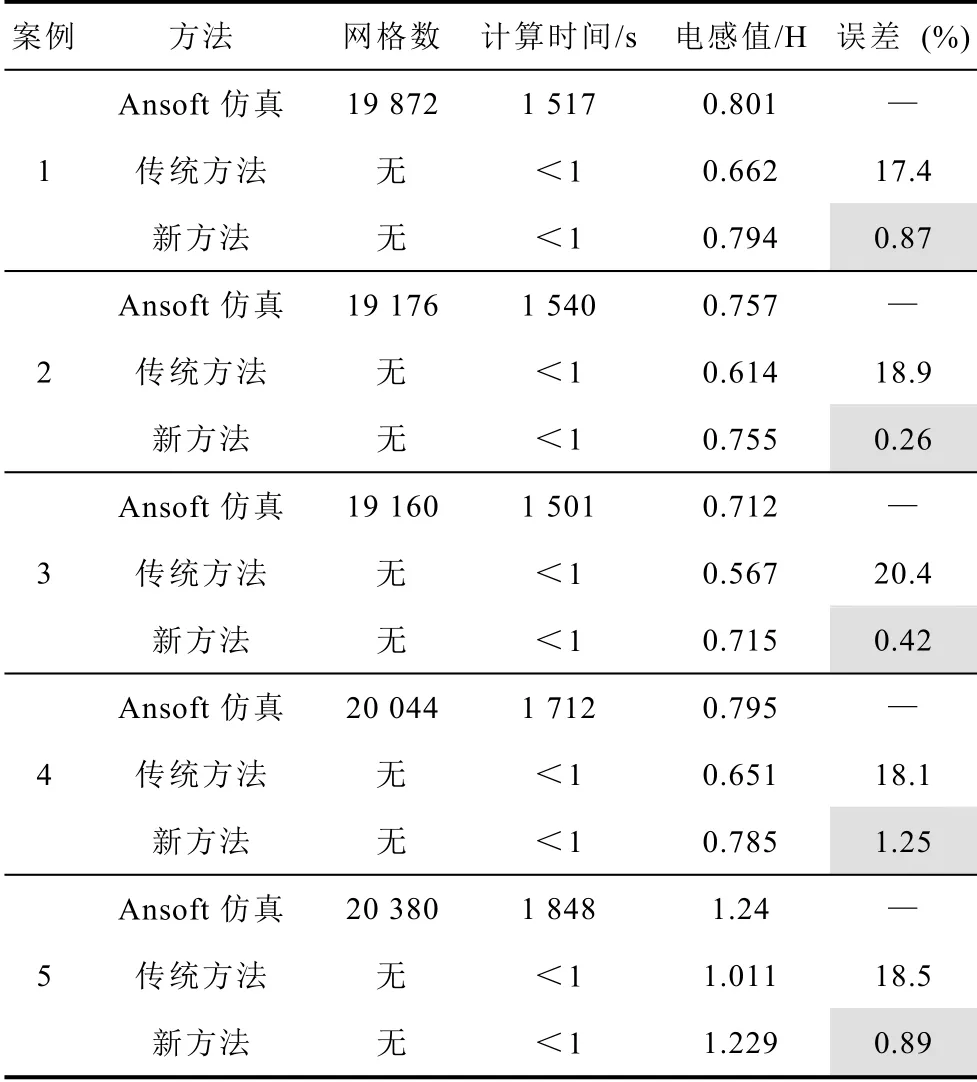
表2 仿真計算對比Tab.2 Comparison between simulation and calculation

為了驗證本文所述方案在不同磁結構下的計算可行性，本文同時搭建了文獻[14]所述的三柱式限流器結構并計算其電感值，其結構尺寸參數見表1 中案例5 所示，拓撲結構如圖11 所示。永磁體分為上下三塊，結構不對稱，共同對左柱Ⅰ及上下兩軛產生勵磁磁動勢。此時可將永磁體部分分割為三個區域，如圖11 虛線框所示上下永磁體α 部分及中柱永磁體β部分，并利用前述公式分別計算這三部分各自的永磁體磁導及空氣漏磁導。考慮永磁體漏磁效應，并根據磁路網絡分析，得到其電感值計算公式為

實踐證明，材料費用占施工費用的60%-70%，而材料費用是有材料用量和材料價格兩個方面組成。材料驗收環節能夠保證工程施工現場材料使用合格，減少材料使用過程中因規格不一致、質量達不到要求等原有造成的浪費，使得施工項目實現經濟效益最大化。

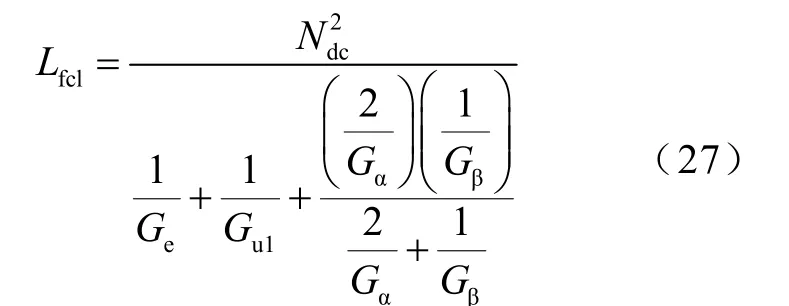
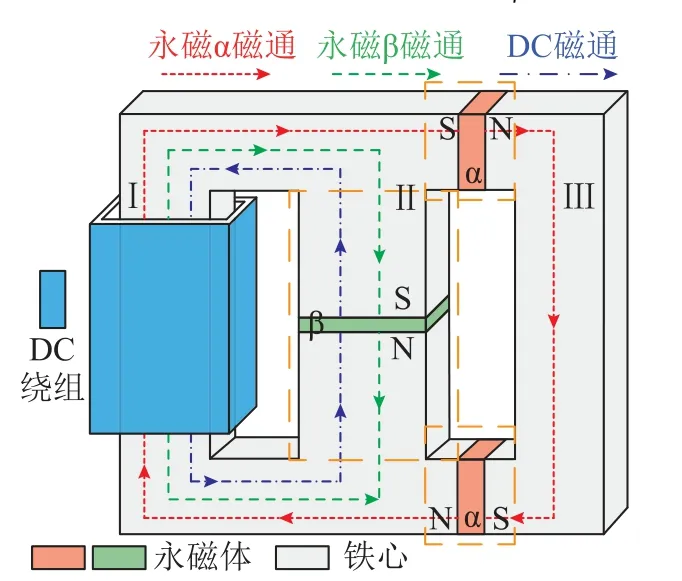
圖11 三柱式限流器結構[14]Fig.11 Three limb FCL topology in Ref[14]

式中，Ge、Gu1、Gα、Gβ分別為左柱、上下軛、考慮漏磁的永磁體α及永磁體β各自部分的總磁導。最終可得到考慮永磁體漏磁效應的限流器電感計算值為1.229H，有限元仿真解為1.24H，二者誤差為0.89%，驗證了本方法在不同磁結構中的有效性。

此外，由于本方法基于數學解析原理，相較需要迭代計算的有限元方法而言節省了大量計算資源。得到限流器尺寸參數后，電感值的計算時間小于1s，較有限元法的數千秒而言速度快了多倍。此外，由于數值解析法得到的是限流器的理論公式解，可以依此進行限流器尺寸參數反演及參數優化工作，設計流程所需時間較前述數值迭代及有限元法而言耗時短，比較適合實際工程使用。

5 實驗驗證

基于上述工作原理，設計并搭建了小容量樣機平臺，驗證所述方法的有效性，樣機采用圖1 所示兩柱式結構拓撲。平臺參數見表3。

表3 實驗模型參數Tab.3 Parameters of the experiment FCL model

以案例1 為例，圖9 所示為模型的網格剖分及磁感應強度分布云圖。由圖9a 所示，有限元模型剖分網格細密，尤其是本文重點關注的永磁體及其鄰近空氣部分剖分精細，解析更為準確，因此可以將該有限元分析結果近似作為準確值進行參照對比，驗證所述方案的有效性。正常工作時兩柱呈現飽和態，故障發生后極短時間內雙柱鐵心退出飽和，與預期工作狀態相吻合。圖10 所示為永磁體附近的漏磁分布云圖，其中lx為鐵心橫軛由右到左的長度，ly為鐵心橫軛自頂端朝空氣方向的長度，其定義圖示詳見圖9b。

式中，imax為系統最大故障電流。

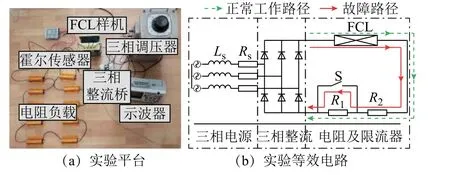
圖12 實驗平臺及等效等效電路Fig.12 Experimental diagram and equivalent circuit

實際直流系統中，直流側往往會串入一個固定電抗實現濾除紋波、限制故障電流上升等作用。為了驗證效果，本實驗首先在直流側輸出端串入20mH 固定電抗，利用示波器錄下正常及故障波形數據，然后將限流器替換固定電抗，進行對比仿真分析。實驗等效電路如圖12b 所示。

通過測量限流器上的電壓電流及系統電流，并采用式（28）計算電感值。

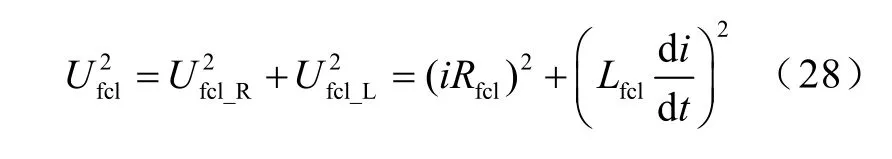
式中，Ufcl、Rfcl、Lfcl、i分別為限流器兩端測量電壓值、限流器本體電阻值、限流器電感值和系統電流值。由式（28）計算可得限流器電感值為

(1) 政府投資。主要包括國家預算內資金和地方政府投資兩種形式。國家預算內資金主要包括中央財政直接投資、國債和國家轉貸資金。其中，國債重點投資西部鐵路建設；地方政府投資以省級政府投資為主，一方面用于股權投資，另一方面用于省級預算內資金支持。

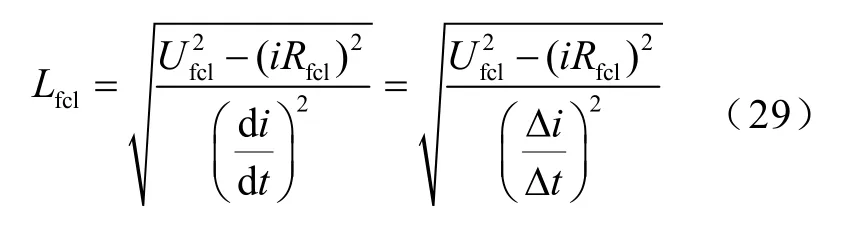
5.1 正常工作狀態

圖13 所示為正常工作時限流器兩端的電壓及電流實驗波形。由于實驗采用三相不可控整流橋產生直流源，因此波形存在六脈頻波動。系統電流波形實際是以單個電阻負載上的電壓表示，由于負載為純阻性，將電壓除以單個負載阻值2? 即可得到實際系統電流。由于示波器同時測得限流器電壓與負載電壓，負極探頭接在同一側，兩個探頭測量電壓方向相反，因此波形存在一正一負的情況。實際波形均為正值，圖13 中實際系統電流值為1A。

在整個市場經濟體系中，資本市場扮演著關鍵角色，處于軸心與中介地位，其是否穩定，會對一國的整體經濟造成直接影響。在1929～1933年間，資本市場所出現的崩潰局面，造成了世界范圍內的大危機。事實表明，資本市場與會計信息間存在著緊密的關系。美國學者在其所編寫的研究報告中指出，會計收益的變化正相關于證券價格的運動方向，且通過全面分析證券價格的運動，能夠對收益結果進行預計，在收益發布一段時間后，價格運動不會出現不正常情況；后經諸多研究得知，將原先的先進先出法更改為后進后出法，會對證券價格造成比較大的影響。

圖13 正常工作下限流器波形Fig.13 Normal waveforms of FCL

因此，由式（29）及圖13 數據可以算得，實驗測量穩態時段內的限流器電感值為18.7mH。有限元仿真值為19.7mH，本文所述計算值為20.0mH。

（2）屬性選擇和屬性值量化。根據臨床經驗或要求從大量病理屬性指標中選擇若干屬性作為決策屬性集，然后對連續型屬性值進行離散化。依據 C4.5 算法構造決策樹，選取燒傷病理屬性項“救治方案”為類別標識屬性。屬性項“燒傷程度”“血壓”“脈搏”“呼吸”“尿量”“意識狀態”“末梢循環”“血常規”“血生物化學”和“凝血酶原時間”作為決策屬性集。

（26）長刺帶葉苔 Pallavicinia subciliata（Austin）Steph.李粉霞等（2011）

5.2 故障限流狀態

圖14 所示為故障發生后時限流器兩端的電壓及電流實驗波形。同樣，由于示波器同時測得限流器電壓與負載電壓，負極探頭接在同一側，兩個探頭測量電壓方向相反，因此波形存在一正一負的情況。實際系統電流應該是以x軸鏡像翻轉波形，故障時刻由1A 上升至穩態7.5A。由于系統發生故障后系統工作狀態發生劇變，導致紋波與擾動更加明顯。由式（29）及圖14 數據可以算得，實驗測量穩態時段內的限流器電感值為55.3mH，有限元仿真值為53.8mH，本文所述計算值為53.3mH。

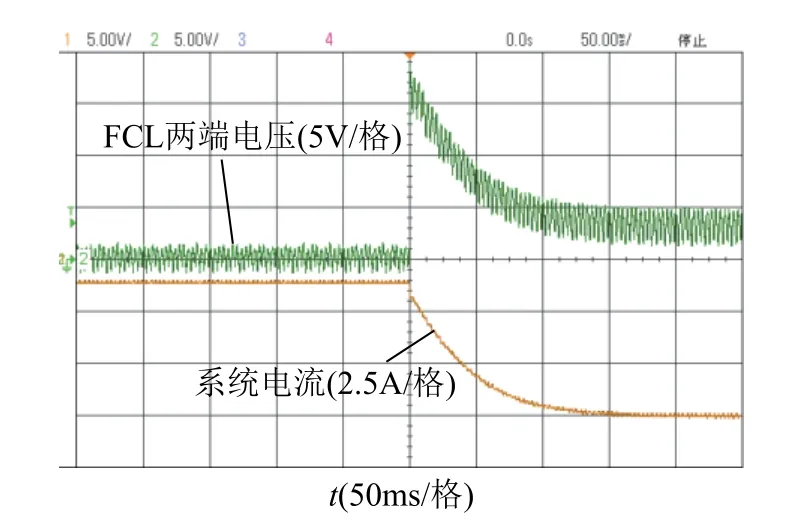
圖14 故障發生后限流器波形Fig.14 Fault waveforms of FCL

5.3 對比分析

限流器電感值結果對比見表4。正常工作時，計算值與仿真值、實驗值間的誤差分別為1.5%、6.9%，總體誤差低于7%；故障發生后，計算值與仿真值、實驗值間的誤差分別為0.9%、3.6%，總體誤差低于4%。在正常態與故障態，仿真、實驗、計算三者吻合度均較好，驗證了本文所述計算方法的有效性。

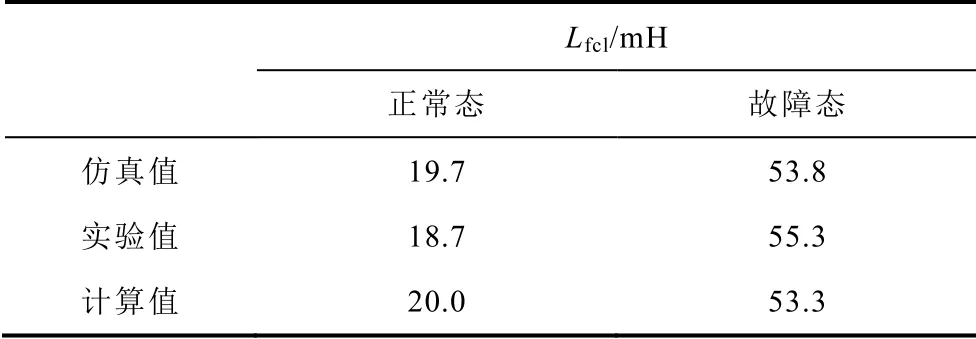
表4 限流器電感值結果對比Tab.4 Results comparison of Lfcl

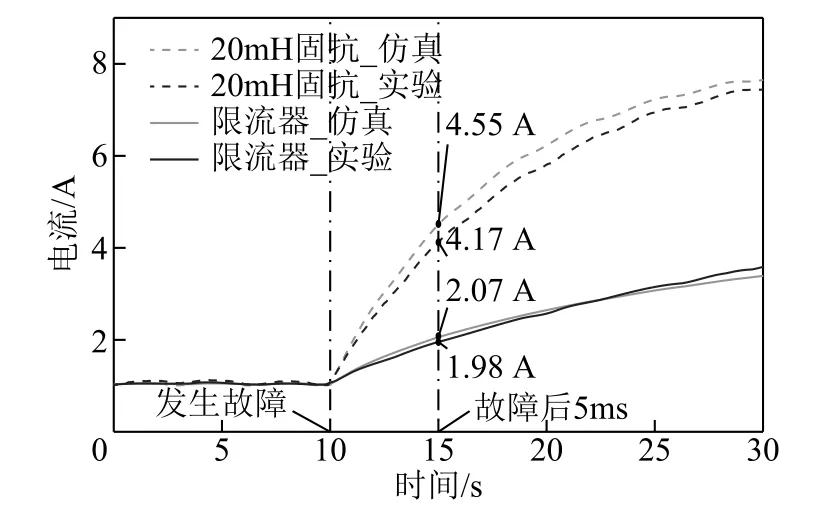
圖15 限流效果對照Fig.15 Fault limiting performance comparison

為了驗證限流器的限流效果，將裝設限流器前后的故障電流進行對比分析，由圖15 可知，當系統僅有20mH 固定電抗時，電流在20ms 內上升至額定電流的近8 倍，需要限流手段限制故障電流上升速率。而將限流器替換固定電抗后，由于限流器正常電感值與20mH 電感接近，正常工作電流與串聯固定電抗時基本吻合，對系統無影響；短路故障發生后，故障電流上升速度顯著降低，5ms 內的故障電流由4.17A 降低至1.98A，限制率達52.5%。由此可知，所述限流器在故障發生時刻有效進入限流狀態，可以顯著降低故障電流上升速度，減少直流側斷路器所需開斷能力。

閑置的電動汽車接入光儲電站需滿足一定的條件后才能參與調制[17]。本文研究離網狀態下不接電動汽車與接入電動汽車后的供電電能質量問題,故電動汽車參與微電網調制的控制目標對象為光儲電站的母線電壓Udc。設置的參考電壓為400 V,超過波動值Ur(5 V)后進行調制。其控制策略如圖4所示。

由仿真與實驗對比可知，20mH 固抗與限流器的仿真與實驗波形基本吻合，限流器的仿真與實驗波形的誤差為4.3%，整體誤差低于5%，驗證了本文所述方案的有效性與準確性。

6 結論

針對現有永磁偏磁型直流限流器設計計算方法缺乏漏磁分析與計算，計算結果不準確，耗費計算資源多的問題，本文提出了一種計及永磁體漏磁效應的磁飽和型高壓直流限流器設計計算方案，通過磁通管區段擬合方法，重構限流器等效磁路的磁阻網絡，得到設計計算方案，最后利用多組有限元仿真及樣機實驗驗證了所述方案的有效性。結論如下：

1）傳統磁阻分析法未計及永磁體漏磁效應，導致永磁部分總磁阻偏低，最終設計計算結果不準確。本方法將永磁鄰近部分空氣漏磁進行分區段擬合，得到準確的磁阻網絡。

2）多組有限元仿真與樣機實驗驗證了所述方法的有效性，相較傳統方法而言，本方法計算誤差由20%左右降至1.3%以內，實驗誤差總體低于7%，驗證了所述方案的有效性。本方案適用于不同設備容量等級及拓撲結構，設計計算效率高，可以廣泛應用于永磁偏磁型鐵心電感設備。