基于長短期記憶網(wǎng)絡(luò)的電力系統(tǒng)量測缺失數(shù)據(jù)恢復(fù)方法

王子馨，胡俊杰，劉寶柱

(華北電力大學(xué)電氣與電子工程學(xué)院，北京市 102206)

0 引 言

隨著電網(wǎng)的快速發(fā)展，我國基本形成了送、受端結(jié)構(gòu)清晰，交、直流協(xié)調(diào)發(fā)展的骨干網(wǎng)架[1-2]。電網(wǎng)規(guī)模的不斷擴大以及電力電子設(shè)備的不斷投入使電網(wǎng)的時空特性日益復(fù)雜[3-4]。傳統(tǒng)的監(jiān)視控制與數(shù)據(jù)采集系統(tǒng)(supervisory control and data acquisition，SCADA)由于數(shù)據(jù)采集密度低以及傳輸過程間隔較長，無法滿足復(fù)雜系統(tǒng)狀態(tài)估計和動態(tài)實時監(jiān)測的要求[5]，而廣域測量系統(tǒng)(wide-area measurement system，WAMS)因其高精度、同步測量等優(yōu)點，在系統(tǒng)動態(tài)分析控制等方面發(fā)揮著越來越重要的作用。

與此同時，隨著電力系統(tǒng)量測技術(shù)的快速發(fā)展及量測成本的不斷下降，量測數(shù)據(jù)呈現(xiàn)快速增長趨勢，逐步具備了大數(shù)據(jù)特征[6]。海量多類型的量測數(shù)據(jù)對電力系統(tǒng)狀態(tài)估計、設(shè)備評估、優(yōu)化運行、事故分析等具有重要意義[7-8]。隨著數(shù)據(jù)挖掘技術(shù)的發(fā)展，海量量測數(shù)據(jù)的傳輸、存儲和分析也成為電力系統(tǒng)領(lǐng)域重要的研究方向。

在此背景下，獲取更為真實可靠的電力系統(tǒng)量測數(shù)據(jù)變得越來越重要。然而由于氣候變化、噪聲干擾、通信延遲等多種復(fù)雜因素影響，數(shù)據(jù)采集、量測、傳輸和存儲過程中往往存在數(shù)據(jù)缺失等問題，導(dǎo)致無法獲取真實可靠的量測數(shù)據(jù)。2009年，美國高德納信息咨詢公司(Gartner)針對140家公司做過一次調(diào)查，其中22%的公司估計其每年因數(shù)據(jù)質(zhì)量問題造成的經(jīng)濟損失高達2 000萬美元。2011年，美國California ISO發(fā)布的“五年計劃”指出北美約有10%至17%的量測數(shù)據(jù)存在質(zhì)量問題。2017年，全球能源互聯(lián)網(wǎng)研究院在《大數(shù)據(jù)背景下電網(wǎng)數(shù)據(jù)質(zhì)量研究與實踐》報告中指出目前我國電力系統(tǒng)量測數(shù)據(jù)存在較為嚴重的質(zhì)量問題。缺失數(shù)據(jù)嚴重影響電力系統(tǒng)狀態(tài)估計、參數(shù)辨識等，導(dǎo)致電網(wǎng)運行狀態(tài)無法及時準確獲取，甚至威脅電網(wǎng)安全穩(wěn)定運行[9-10]。

目前，國內(nèi)外學(xué)者針對缺失數(shù)據(jù)問題提出了眾多處理方法，主要可分為后評估和預(yù)處理兩大分支。后評估是基于狀態(tài)估計的相關(guān)方法。該類方法利用冗余量測和系統(tǒng)拓撲結(jié)構(gòu)，構(gòu)造狀態(tài)方程恢復(fù)缺失數(shù)據(jù)。文獻[11]提出了一種基于擴展卡爾曼濾波的動態(tài)狀態(tài)估計方法，用于估計系統(tǒng)缺失的量測數(shù)據(jù)。文獻[12]利用時間相關(guān)性和測量一致性，提出了一種廣義魯棒估計器，實現(xiàn)缺失量測數(shù)據(jù)的恢復(fù)。后評估的方法雖然可實現(xiàn)缺失數(shù)據(jù)的準確恢復(fù)，但其估計時間較長，需要系統(tǒng)拓撲參數(shù)。預(yù)處理則為數(shù)據(jù)驅(qū)動，通過研究已知數(shù)據(jù)，獲取數(shù)據(jù)規(guī)律實現(xiàn)對缺失數(shù)據(jù)的補充。文獻[13]提出了一種線性插值的方法，恢復(fù)系統(tǒng)中缺失的相量數(shù)據(jù)。在此基礎(chǔ)上，文獻[14]將改進三次樣條插值與優(yōu)先級分配策略相結(jié)合，提高了系統(tǒng)動態(tài)下缺失數(shù)據(jù)的恢復(fù)精度。文獻[15]提出基于低秩矩陣填充理論的電能質(zhì)量感知數(shù)據(jù)補全方法。文獻[16]計及數(shù)據(jù)缺失曲線相似度，同樣將低秩矩陣填充理論用于恢復(fù)缺失的電量數(shù)據(jù)。文獻[17]則提出了一種基于張量分解的數(shù)據(jù)恢復(fù)方法，將數(shù)據(jù)分解為時間、位置和變量三個維度。同時，隨著深度學(xué)習(xí)技術(shù)在電力系統(tǒng)中的應(yīng)用，電力系統(tǒng)量測數(shù)據(jù)的時序性、相關(guān)性、規(guī)律性都可以作為缺失數(shù)據(jù)恢復(fù)的重要依據(jù)。文獻[18]采用淺層自動編碼器神經(jīng)網(wǎng)絡(luò)對數(shù)據(jù)間特性進行學(xué)習(xí)實現(xiàn)數(shù)據(jù)恢復(fù)。文獻[19]提出了改進生成式對抗網(wǎng)絡(luò)學(xué)習(xí)量測數(shù)據(jù)間復(fù)雜的時空特性，利用真實性約束及上下文相似性約束優(yōu)化隱變量，從而實現(xiàn)數(shù)據(jù)準確恢復(fù)。但上述網(wǎng)絡(luò)模型較為復(fù)雜，不易于應(yīng)用。此外，文獻[20]利用電力系統(tǒng)量測數(shù)據(jù)的時序特性，提出了一種基于長短期記憶(long short-term memory，LSTM)網(wǎng)絡(luò)的數(shù)據(jù)生成方法。文獻[21]同樣基于長短期記憶網(wǎng)絡(luò)提出了負荷短期預(yù)測的方法。LSTM網(wǎng)絡(luò)可有選擇記憶序列信息，對量測數(shù)據(jù)有著良好的適用性，且易于實現(xiàn)。

基于上述背景，本文計及電力系統(tǒng)量測數(shù)據(jù)的時序特性，提出一種基于長短期記憶網(wǎng)絡(luò)的電力系統(tǒng)量測缺失數(shù)據(jù)恢復(fù)方法。該方法可構(gòu)造已有數(shù)據(jù)對缺失數(shù)據(jù)的映射，并可有選擇地記憶對缺失數(shù)據(jù)影響較大的信息。同時為進一步提高系統(tǒng)不同狀態(tài)和不同缺失位置下的恢復(fù)精度，提出基于隨機森林的狀態(tài)辨識方法和缺失數(shù)據(jù)恢復(fù)策略。最終通過仿真數(shù)據(jù)和實測數(shù)據(jù)進行驗證，結(jié)果表明該方法依靠數(shù)據(jù)驅(qū)動，在不同數(shù)量的缺失情況下恢復(fù)的數(shù)據(jù)均能保持較高的準確率。

1 基于LSTM網(wǎng)絡(luò)的缺失數(shù)據(jù)恢復(fù)

本節(jié)將重點介紹LSTM網(wǎng)絡(luò)單元結(jié)構(gòu)，建立雙層全連接的LSTM網(wǎng)絡(luò)結(jié)構(gòu)模型，并分析所提LSTM網(wǎng)絡(luò)應(yīng)用于電力系統(tǒng)缺失數(shù)據(jù)恢復(fù)的適用性。

1.1 LSTM網(wǎng)絡(luò)單元結(jié)構(gòu)

電力系統(tǒng)量測數(shù)據(jù)呈現(xiàn)時序特性，本文以廣域測量系統(tǒng)中同步相量測量單元(phasor measurement units，PMUs)量測數(shù)據(jù)為例進行分析。系統(tǒng)某動態(tài)條件下量測的結(jié)果如圖1所示。幅值X可看作時間t的函數(shù)，X=f(t)。假設(shè)在t3—t4時段幅值數(shù)據(jù)缺失。

圖1 動態(tài)數(shù)據(jù)示意圖

LSTM網(wǎng)絡(luò)是一種特殊的循環(huán)神經(jīng)網(wǎng)絡(luò)(recurrent neural network，RNN)，由于其獨特的門結(jié)構(gòu)，使梯度沿時間反向傳播時可經(jīng)過較長的距離，從而降低梯度消失的可能。同時，作為一種用于序列學(xué)習(xí)的體系結(jié)構(gòu)，LSTM網(wǎng)絡(luò)可有選擇地篩選并遺忘之前序列中的某些信息以減少對后續(xù)序列的影響[22-23]。因此，LSTM網(wǎng)絡(luò)可用于如圖1所示的電力系統(tǒng)量測數(shù)據(jù)的處理，其單元結(jié)構(gòu)如圖2所示。

圖2 LSTM網(wǎng)絡(luò)單元結(jié)構(gòu)

LSTM網(wǎng)絡(luò)在傳統(tǒng)RNN的隱含層中增加了一個細胞狀態(tài)Ct，并利用遺忘門ft、輸入門it和輸出門ot實現(xiàn)對信息傳遞的控制。在t時刻，該網(wǎng)絡(luò)單元有3個輸入和2個輸出。輸入分別為當(dāng)前時刻的輸入xt，上一時刻的輸出ht-1以及上一時刻的細胞狀態(tài)Ct-1。輸出為當(dāng)前時刻的輸出ht和當(dāng)前時刻的細胞狀態(tài)Ct。其中，ht負責(zé)記憶序列短期特征，Ct負責(zé)記憶序列長期特征。

遺忘門ft決定細胞狀態(tài)中保存或丟棄前序信息長期特征的程度，可表示為：

ft=σ(Wf·[ht-1,xt]+bf)

(1)

式中：ft為t-1時刻輸出ht-1、t時刻輸入xt和偏置項bf的激活值，激活函數(shù)為sigmoid，激活函數(shù)將ft縮放至0(完全遺忘)和1(完全記憶)之間；Wf為權(quán)重項，包括Wfx和Wfh。

輸入門it確定如何更新細胞狀態(tài)，即將新的信息選擇性地記憶到細胞狀態(tài)Ct，公式如下：

(2)

輸出門ot決定當(dāng)前時刻的輸入，與輸入門類似，ht由ot和Ct確定攜帶的信息，公式如下：

(3)

式中：Wo為權(quán)重項，包括Wox和Who；bo為偏置項。

基于以上分析，將LSTM網(wǎng)絡(luò)應(yīng)用于如圖1所示的幅值數(shù)據(jù)恢復(fù)，針對t3—t4時段的缺失數(shù)據(jù)，遺忘門會有選擇地增加前序信息中類似時段的數(shù)據(jù)(如t1—t2時段)，遺忘其余部分時段的數(shù)據(jù)。同時由于幅值在t3時刻前正逐漸減小，輸入門會記憶序列短期的變化規(guī)律，將幅值逐漸減小的信息增加到細胞Ct中，最后通過輸出門決定輸出。通過上述若干非線性變化，可實現(xiàn)高維函數(shù)的逼近，挖掘幅值數(shù)據(jù)中的隱藏信息以實現(xiàn)t3—t4時段缺失數(shù)據(jù)的恢復(fù)。

1.2 雙層全連接LSTM網(wǎng)絡(luò)缺失數(shù)據(jù)恢復(fù)

為了更好耦合電力系統(tǒng)量測數(shù)據(jù)的時序特性，本文組合多個LSTM網(wǎng)絡(luò)單元，提出一種雙層全連接的LSTM網(wǎng)絡(luò)結(jié)構(gòu)，可實現(xiàn)已知數(shù)據(jù)到缺失數(shù)據(jù)的映射，如圖3所示。

圖3 雙層LSTM網(wǎng)絡(luò)模型

設(shè)時間t內(nèi)，幅值數(shù)據(jù)為D=X1,X2, …,Xmn。對幅值數(shù)據(jù)標準化處理，令m個數(shù)據(jù)為1組，共n組，首先建立模型的輸入層。每組數(shù)據(jù)對應(yīng)一個輸入xi，其中x1={X1,X2, …,Xm},x2={X2,X3, … ,Xm+1}, …,xn={X(n-1)m+1, X(n-1)m+2, … ,Xnm}。然后將多個LSTM單元組合為一層，通過兩層LSTM網(wǎng)絡(luò)與Dense全連接組成形成隱藏層。第一層LSTM網(wǎng)絡(luò)將輸入的xi通過特定結(jié)構(gòu)隱投影到高維空間，其中包含了幅值數(shù)據(jù)Xi,Xi+1, … ,Xi+m間的相互關(guān)系。同時根據(jù)獨特的門結(jié)構(gòu)進行判斷，決定記憶或遺忘某些特征。第二層LSTM網(wǎng)絡(luò)將hi提煉為與恢復(fù)數(shù)據(jù)X′m+k+i具有線性關(guān)系的多變量。Dense全連接層可視為回歸層(regression layer)，將LSTM網(wǎng)絡(luò)提取的特征hi(狀態(tài)變量)轉(zhuǎn)化為恢復(fù)的缺失數(shù)據(jù)X′m+k+i。輸出層最后通過迭代和反標準化實現(xiàn)對缺失數(shù)據(jù)的恢復(fù)。

本文對于上述網(wǎng)絡(luò)采用反向傳播算法(backpropagation through time algorithm, BPTT)[24]，計算網(wǎng)絡(luò)中各參數(shù)值。通過反向計算每個神經(jīng)元的誤差項δ，誤差項將沿著時間反向并向上一層傳播。根據(jù)誤差項可得各時刻權(quán)重梯度，即可完成所提LSTM網(wǎng)絡(luò)訓(xùn)練，同時也避免了梯度爆炸和梯度消失的問題。

2 基于隨機森林的量測數(shù)據(jù)狀態(tài)辨識

由于量測數(shù)據(jù)可能處于系統(tǒng)不同運行狀態(tài)下，而不同狀態(tài)下的數(shù)據(jù)時序特性不同，所需LSTM網(wǎng)絡(luò)模型參數(shù)不同，因此需提出一種數(shù)據(jù)狀態(tài)的辨識方法。隨機森林方法綜合Bagging集成學(xué)習(xí)算法和隨機子空間方法的思想，算法構(gòu)建簡單，準確性高，比傳統(tǒng)決策樹方法具有更強的泛化能力[25]，因此，本文提出基于隨機森林的數(shù)據(jù)狀態(tài)辨識方法。電力系統(tǒng)穩(wěn)態(tài)量測數(shù)據(jù)和動態(tài)量測數(shù)據(jù)如圖4所示。

圖4 穩(wěn)態(tài)數(shù)據(jù)和動態(tài)數(shù)據(jù)

圖4中，方框表示量測數(shù)據(jù)D=X1,X2, … ,Xkj，藍色方框表示穩(wěn)態(tài)數(shù)據(jù)，紅色方框表示動態(tài)數(shù)據(jù)，其中穩(wěn)態(tài)數(shù)據(jù)和動態(tài)數(shù)據(jù)各占50%。令j個數(shù)據(jù)為一組，共k組，數(shù)據(jù)量Q=k×j。設(shè)穩(wěn)態(tài)數(shù)據(jù)組的狀態(tài)標簽s1=0，動態(tài)數(shù)據(jù)組的狀態(tài)標簽s2=1。由于穩(wěn)態(tài)數(shù)據(jù)較為平穩(wěn)，離散程度較低，動態(tài)數(shù)據(jù)波動性強，離散程度高，且變化規(guī)律明顯，所以將各數(shù)據(jù)組的均值a、標準差b、極值差c、斜率均值d和斜率極值e作為特征屬性，通過學(xué)習(xí)上述特征屬性實現(xiàn)對兩類數(shù)據(jù)的辨識。

首先通過Bootstrap重采樣方法對樣本數(shù)據(jù)D進行有放回的m次抽樣，生成m個訓(xùn)練子集S，其中訓(xùn)練子集樣本數(shù)應(yīng)小于Q。然后從上述5個特征屬性中隨機選取w個，對各訓(xùn)練子集構(gòu)造分類回歸樹(classification and regression tree，CART)。分類回歸樹基于基尼系數(shù)選擇特征，構(gòu)造過程如下。

1)設(shè)訓(xùn)練子集S中存在穩(wěn)態(tài)數(shù)據(jù)和動態(tài)數(shù)據(jù)，則訓(xùn)練子集的基尼系數(shù)為：

(4)

式中：p1表示子集中穩(wěn)態(tài)數(shù)據(jù)的概率；p2表示動態(tài)數(shù)據(jù)的概率。

2)假設(shè)根據(jù)特征a中某屬性值ai劃分訓(xùn)練子集，訓(xùn)練子集分為S1和S2，則在特征a下的基尼系數(shù)為：

(5)

式中：|·|表示訓(xùn)練子集中的樣本數(shù)。

上述各特征均為連續(xù)特征，需離散化處理。設(shè)連續(xù)特征均值a有z個不同取值，將這些值從小到大排列，得到特征值集合{a1,a2,… ,az}，取各區(qū)間[ai,ai+1)中點作為候選劃分點，可得集合Pa：

(6)

3)根據(jù)式(5)，計算各候選劃分點的基尼系數(shù)，將基尼系數(shù)最小的候選劃分點作為分支節(jié)點對訓(xùn)練集中數(shù)據(jù)進行分類，不斷遞歸計算，直至形成分類回歸樹。

最后，重復(fù)進行M次重采樣和特征選取，可得M個決策樹，形成隨機森林。將測試樣本輸入隨機森林，對各決策樹的辨識結(jié)果采用基于集成投票的思想，選出票數(shù)最多的數(shù)據(jù)狀態(tài)，得到隨機森林方法的辨識結(jié)果。

3 量測缺失數(shù)據(jù)恢復(fù)策略及流程

考慮到電力系統(tǒng)缺失數(shù)據(jù)的隨機性，本文提出了一種考慮不同缺失位置的量測數(shù)據(jù)恢復(fù)策略，如表1所示。在固定時間窗的前提下，對時間窗內(nèi)的量測缺失數(shù)據(jù)進行恢復(fù)。

表1 不同位置下恢復(fù)策略

綜上所述，結(jié)合雙層全連接的LSTM網(wǎng)絡(luò)、隨機森林的數(shù)據(jù)狀態(tài)辨識以及不同缺失位置恢復(fù)策略，可得電力系統(tǒng)量測缺失數(shù)據(jù)恢復(fù)流程，如圖5所示。首先將包含缺失數(shù)據(jù)的樣本輸入訓(xùn)練好的隨機森林中進行數(shù)據(jù)狀態(tài)辨識。若為穩(wěn)態(tài)數(shù)據(jù)，則根據(jù)缺失數(shù)據(jù)在整體數(shù)據(jù)中的具體位置選擇對應(yīng)的恢復(fù)策略，并輸入LSTM-s網(wǎng)絡(luò)進行恢復(fù)；若為動態(tài)數(shù)據(jù)，則在判斷缺失數(shù)據(jù)所處位置后，根據(jù)其對應(yīng)的恢復(fù)策略，輸入LSTM-d網(wǎng)絡(luò)進行恢復(fù)。其中LSTM-s網(wǎng)絡(luò)參數(shù)利用穩(wěn)態(tài)數(shù)據(jù)訓(xùn)練，LSTM-d網(wǎng)絡(luò)參數(shù)利用動態(tài)數(shù)據(jù)訓(xùn)練。

圖5 缺失數(shù)據(jù)恢復(fù)流程

4 算例分析

本文方法計算環(huán)境：CPU為Core i7-9700k，主頻為3.6 GHz，內(nèi)存為16 GB，GPU為NVIDIA GTX 2070，編程平臺為Python 3.7。

經(jīng)大量仿真測試，LSTM網(wǎng)絡(luò)及隨機森林的最優(yōu)參數(shù)按下列方法進行設(shè)置。LSTM網(wǎng)絡(luò)參數(shù)設(shè)置如下：輸入層維度為1；隱藏層層數(shù)為3，第一層LSTM神經(jīng)元個數(shù)為64，第二層LSTM神經(jīng)元個數(shù)為64，Dense層神經(jīng)元個數(shù)為32；輸出層維度為1，采用Adam優(yōu)化算法更新LSTM網(wǎng)絡(luò)權(quán)重。隨機森林方法的參數(shù)設(shè)置如下：決策樹個數(shù)M為81，隨機特征數(shù)w為3。若采用其他參數(shù)，缺失數(shù)據(jù)恢復(fù)精度將存在不同程度的降低。

為驗證本文所提方法的有效性，利用如圖6所示的IEEE 10機39節(jié)點系統(tǒng)仿真數(shù)據(jù)與西北地區(qū)某750 kV變電站實測母線電壓幅值數(shù)據(jù)進行驗證并與現(xiàn)有方法進行對比。

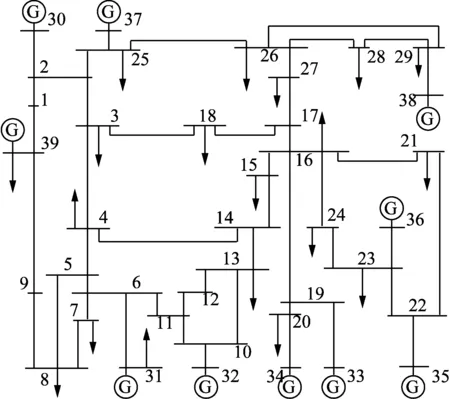
圖6 IEEE 10機39節(jié)點拓撲

4.1 仿真數(shù)據(jù)測試

在仿真系統(tǒng)穩(wěn)態(tài)下，設(shè)置0.2 Hz的低頻振蕩，記錄母線1電壓幅值數(shù)據(jù)，上送頻率100 Hz，仿真數(shù)據(jù)如圖7所示。由圖7可知，系統(tǒng)運行約1.6 s后發(fā)生低頻振蕩。藍色表示穩(wěn)態(tài)數(shù)據(jù)為160個，紅色表示動態(tài)數(shù)據(jù)為240個。

圖7 穩(wěn)態(tài)和動態(tài)仿真數(shù)據(jù)

首先設(shè)置不同的缺失數(shù)據(jù)占比，仿真次數(shù)為100次。采用本文所提隨機森林方法測試數(shù)據(jù)狀態(tài)辨識精度(對應(yīng)圖5中隨機森林部分)，并與文獻[25]的決策樹法進行對比，結(jié)果如圖8所示。

圖8 仿真數(shù)據(jù)狀態(tài)辨識結(jié)果

由圖8可知，隨著缺失數(shù)據(jù)占比的增加，兩種方法的辨識精度均不同程度降低，當(dāng)缺失數(shù)據(jù)占比為10%至60%時，本文所提隨機森林的數(shù)據(jù)狀態(tài)辨識方法的平均準確率約為98.5%，并且均高于決策樹法。

然后針對圖7的仿真數(shù)據(jù)，在缺失數(shù)據(jù)數(shù)占比為10%時，改變?nèi)笔?shù)據(jù)位置，結(jié)合所提隨機森林狀態(tài)辨識與LSTM網(wǎng)絡(luò)恢復(fù)方法對缺失數(shù)據(jù)進行恢復(fù)(對應(yīng)圖5中LSTM網(wǎng)絡(luò)部分)，并與僅采用LSTM網(wǎng)絡(luò)的恢復(fù)方法、文獻[13]的插值法和文獻[16]的低秩法對比，恢復(fù)數(shù)據(jù)的均方根誤差見表2。

表2 不同缺失位置對數(shù)據(jù)恢復(fù)精度的影響

由表2可知，本文所提結(jié)合隨機森林狀態(tài)辨識與LSTM網(wǎng)絡(luò)恢復(fù)方法受缺失數(shù)據(jù)位置的影響較小；由于不同缺失位置下數(shù)據(jù)狀態(tài)不同，因此僅采用LSTM網(wǎng)絡(luò)的恢復(fù)方法受其影響較大，無法準確恢復(fù)缺失數(shù)據(jù)，須結(jié)合基于隨機森林的數(shù)據(jù)狀態(tài)辨識方法；插值法無法較好地恢復(fù)動態(tài)下的數(shù)據(jù)；低秩法在過渡階段的恢復(fù)誤差較大。中部數(shù)據(jù)為穩(wěn)態(tài)到動態(tài)的過渡階段，因此4種方法在該情況下的恢復(fù)精度均有不同程度的降低。

接下來將缺失數(shù)據(jù)設(shè)置位于序列中部，改變?nèi)笔д急龋瑢Ρ?種方法的恢復(fù)結(jié)果，如表3所示。

表3 不同缺失占比對數(shù)據(jù)恢復(fù)精度的影響

由表3可知，插值法在缺失數(shù)據(jù)較多時，無法準確恢復(fù)缺失數(shù)據(jù)。在缺失占比為30%時，僅本文所提方法可有效恢復(fù)缺失數(shù)據(jù)，可見本文所提方法受缺失占比的影響較小。

在此基礎(chǔ)上，設(shè)置圖7中的動態(tài)數(shù)據(jù)存在20%的缺失數(shù)據(jù)，采用所提雙層全連接的LSTM網(wǎng)絡(luò)對缺失數(shù)據(jù)進行恢復(fù)，并與插值法、低秩法進行對比。由于該過程未涉及數(shù)據(jù)狀態(tài)辨識，因此無須使用基于隨機森林的狀態(tài)辨識方法，恢復(fù)結(jié)果如圖9所示。

圖9 動態(tài)缺失數(shù)據(jù)恢復(fù)結(jié)果

通過計算可知，本文所提量測缺失數(shù)據(jù)恢復(fù)方法的均方根誤差為0.18%，插值法的均方根誤差為4.61%，低秩方法的均方根誤差為1.17%。可見本文所提方法恢復(fù)精度較高，可有效恢復(fù)動態(tài)下的缺失數(shù)據(jù)。

4.2 現(xiàn)場數(shù)據(jù)驗證

選用西北地區(qū)某750 kV變電站實測母線電壓幅值數(shù)據(jù)驗證所提方法的有效性。實測數(shù)據(jù)均為穩(wěn)態(tài)數(shù)據(jù)，如圖10所示。在不同母線實測數(shù)據(jù)中設(shè)置多種動態(tài)數(shù)據(jù)，首先驗證所提數(shù)據(jù)狀態(tài)辨識方法的有效性，結(jié)果如表4所示。

圖10 現(xiàn)場實測母線電壓幅值數(shù)據(jù)

表4 不同方法對現(xiàn)場數(shù)據(jù)狀態(tài)辨識結(jié)果對比

由表4可知，對于不同母線實測數(shù)據(jù)，隨機森林方法的辨識準確率均高于決策樹法，即隨機森林方法具有較好的泛化性，不受現(xiàn)場噪聲等的影響。

在如圖10所示的位置設(shè)置缺失數(shù)據(jù)，采用時間窗為0.5 s的量測數(shù)據(jù)進行恢復(fù)，保證缺失數(shù)據(jù)的位置位于中部，并與插值法、低秩法進行對比，結(jié)果如圖11所示。

圖11 現(xiàn)場實測數(shù)據(jù)恢復(fù)結(jié)果

由圖11可知，本文所提恢復(fù)方法的均方根誤差為0.94%，插值法的均方根誤差為3.1%，低秩法的均方根誤差為2.6%。可見本文所提的LSTM網(wǎng)絡(luò)的缺失數(shù)據(jù)恢復(fù)方法對實測缺失數(shù)據(jù)的恢復(fù)精度最高，可適用于現(xiàn)場量測數(shù)據(jù)。

5 結(jié) 論

本文提出了一種基于長短期記憶網(wǎng)絡(luò)的電力系統(tǒng)量測缺失數(shù)據(jù)恢復(fù)方法。該方法可有效辨識系統(tǒng)量測數(shù)據(jù)的不同狀態(tài)，進而實現(xiàn)對量測缺失數(shù)據(jù)的準確恢復(fù)，有效提高數(shù)據(jù)的可用性。本文研究主要結(jié)論如下：

1)基于長短期記憶網(wǎng)絡(luò)對電力系統(tǒng)量測數(shù)據(jù)規(guī)律選擇記憶的特性，提出了一種雙層全連接的LSTM網(wǎng)絡(luò)模型，實現(xiàn)從已知數(shù)據(jù)到缺失數(shù)據(jù)的映射。

2)提出一種基于隨機森林的數(shù)據(jù)狀態(tài)辨識方法，有效區(qū)別系統(tǒng)穩(wěn)態(tài)、動態(tài)數(shù)據(jù)，為后續(xù)缺失數(shù)據(jù)恢復(fù)提供基礎(chǔ)。

3)提出一種考慮缺失數(shù)據(jù)位置的恢復(fù)策略，根據(jù)數(shù)據(jù)的缺失位置匹配相應(yīng)的恢復(fù)策略提高恢復(fù)精度。

4)通過仿真和實測數(shù)據(jù)測試表明所提方法可有效恢復(fù)系統(tǒng)穩(wěn)態(tài)、動態(tài)下的缺失數(shù)據(jù)，亦可提高現(xiàn)有方法的恢復(fù)精度。

本文暫未計及不良數(shù)據(jù)對量測缺失數(shù)據(jù)恢復(fù)的影響，后續(xù)將進一步針對不良數(shù)據(jù)檢測辨識展開研究。