IFM系統(tǒng)的雙交疊信號(hào)分析及改進(jìn)*
王洪迅,王連河,王建,王士巖,王洪雷
(1.空軍工程大學(xué) 航空工程學(xué)院,陜西 西安 710038;2.中國(guó)人民解放軍93286部隊(duì),遼寧 沈陽(yáng) 110141;3.中國(guó)人民解放軍93149部隊(duì),甘肅 酒泉 735018)
0 引言
RWR(radar-warning receiver)/ESM(electronic warfare support measure)系統(tǒng)通過(guò)探測(cè)雷達(dá)信號(hào),來(lái)識(shí)別載機(jī)所面臨的威脅并進(jìn)行告警,其中多以瞬時(shí)測(cè)頻(instantaneous frequency measure,IFM)技術(shù)進(jìn)行頻率測(cè)試[1-3]。IFM瞬時(shí)帶寬寬,動(dòng)態(tài)范圍大,分辨力高,測(cè)試速度快,可精測(cè)單個(gè)信號(hào),但傳統(tǒng)上認(rèn)為對(duì)同時(shí)到達(dá)信號(hào)測(cè)頻不正確。工程實(shí)踐中一般設(shè)置同時(shí)到達(dá)信號(hào)檢測(cè)電路,以標(biāo)記測(cè)頻錯(cuò)誤[1-2]。文獻(xiàn)[4]表明,若信號(hào)流超過(guò)500萬(wàn)脈沖數(shù)/s,IFM面臨同時(shí)到達(dá)信號(hào)的概率超過(guò)10%(2個(gè))和2%(3個(gè))。由文獻(xiàn)[4]可知,信號(hào)同時(shí)到達(dá)只是信號(hào)交疊的特例,IFM的信號(hào)交疊概率要遠(yuǎn)大于信號(hào)同時(shí)到達(dá)的概率。傳統(tǒng)的IFM把交疊信號(hào)當(dāng)作一個(gè)信號(hào)進(jìn)行測(cè)頻,這樣的處理方式只能得到一個(gè)信號(hào)的頻率,且存在一定的測(cè)頻誤差,誤差的大小由2個(gè)信號(hào)的幅度、頻率差等多種因素決定,因此傳統(tǒng)上對(duì)交疊信號(hào)的處理方式極大地影響了IFM效能[4]。
諸多文獻(xiàn)對(duì)IFM系統(tǒng)的交疊信號(hào)處理能力有深入分析。文獻(xiàn)[5]提出一種對(duì)IFM交疊信號(hào)的處理方法,該方法在一定信噪比和兩信號(hào)功率比的情況下,能夠估計(jì)一個(gè)信號(hào)的頻率,但無(wú)法估計(jì)交疊信號(hào)中另一個(gè)信號(hào)的頻率。文獻(xiàn)[6]雖然對(duì)瞬時(shí)測(cè)頻的多值問(wèn)題進(jìn)行了分析,但提出的改進(jìn)方案不能測(cè)量交疊信號(hào)頻率。文獻(xiàn)[7-9]基于傅里葉變換原理,對(duì)傳統(tǒng)的IFM加以改進(jìn)。其中文獻(xiàn)[7-8]應(yīng)用對(duì)短時(shí)傅里葉變換結(jié)果進(jìn)行插值的方法,提高測(cè)頻精度,可以準(zhǔn)確地估計(jì)多個(gè)交疊信號(hào)的頻率;文獻(xiàn)[9]采用多結(jié)構(gòu)的短時(shí)測(cè)頻算法和基于線性調(diào)頻Z變換(chirp Z transform,CZT)算法,縮短了測(cè)頻時(shí)間,提高了測(cè)頻精度。但這幾種方法的瞬時(shí)帶寬不夠?qū)挕N墨I(xiàn)[10]利用奇異譜分析(singular spectrum analysis,SSA)構(gòu)建偽陣列信號(hào),采用盲源分離算法(blind source separation,BSS)實(shí)現(xiàn)信號(hào)分離,但對(duì)頻譜相近或重疊的交疊信號(hào),此方法失效。文獻(xiàn)[11]基于單比特接收算法,滑動(dòng)快速傅里葉變換(fast Fourier transform,FFT)算法,提出了寬帶單比特IFM接收技術(shù),可估計(jì)交疊信號(hào)頻率,具備大帶寬、實(shí)時(shí)處理、高頻率分辨率等優(yōu)點(diǎn),但這種算法的動(dòng)態(tài)范圍不夠大,測(cè)頻精度沒(méi)有傳統(tǒng)IFM測(cè)頻精度高。
那么能否在保持IFM接收機(jī)原有優(yōu)點(diǎn)的基礎(chǔ)上,使其具備處理交疊信號(hào)的能力呢?本文通過(guò)分析交疊信號(hào)作用于IFM系統(tǒng)的工作機(jī)理,發(fā)現(xiàn)其具備這一能力。
1 IFM系統(tǒng)概述
典型IFM單元如圖1所示[1],其基本組成為:功分器、延遲線、90°電橋、平方率檢波器和差分放大器。
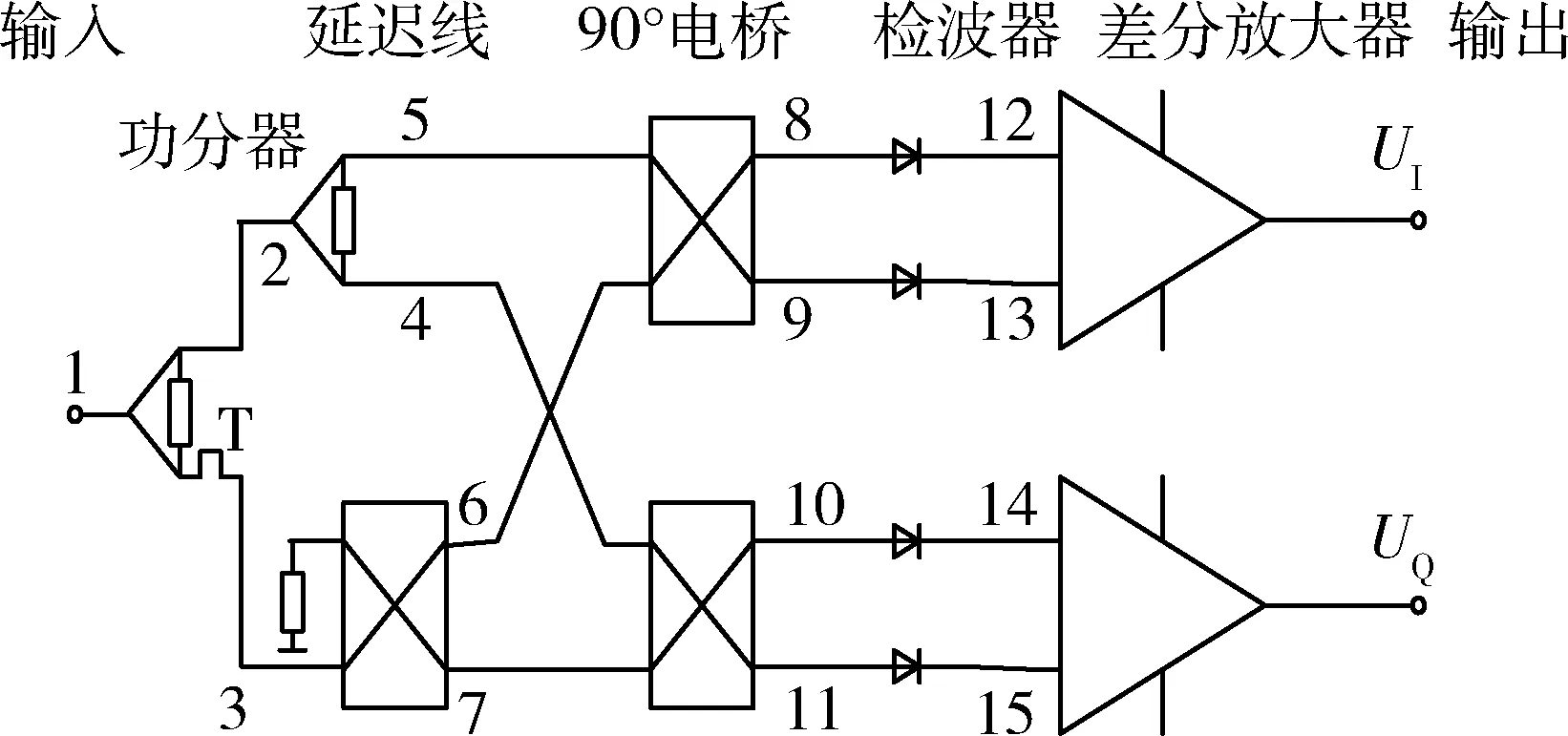
圖1 實(shí)用微波鑒相器結(jié)構(gòu)示意圖
(1)
式中:K為檢波器系數(shù);A為信號(hào)幅度;φ為相角。
φ=2πfT,
(2)
式中:T為延遲線的時(shí)間延遲;f為輸入信號(hào)的載頻。
由式(1),(2)得,信號(hào)頻率為
(3)
為了解決頻段覆蓋和分辨力的矛盾,工程上采用圖2所示IFM并聯(lián)結(jié)構(gòu)[12],其主要有2種典型特征:
(1) 極性量化器+編碼矯正結(jié)構(gòu)。為了快速獲取測(cè)量結(jié)果,通常采用極性量化器,由于各個(gè)支路測(cè)量結(jié)果有模糊,通過(guò)編碼矯正邏輯,以獲取正確的測(cè)量結(jié)果。
(2) 視頻檢波信號(hào)經(jīng)整形,再經(jīng)一定時(shí)間的延遲,形成鎖存脈沖,從而獲得信號(hào)的測(cè)量結(jié)果。
由于以上2個(gè)特征,使IFM對(duì)某一個(gè)具體的未知雷達(dá)脈沖信號(hào)只進(jìn)行一次量化采樣,輸出為當(dāng)前時(shí)刻的頻率二進(jìn)制碼[1],因此這種傳統(tǒng)的IFM系統(tǒng)對(duì)交疊信號(hào)測(cè)頻時(shí)僅輸出一個(gè)結(jié)果。大量實(shí)驗(yàn)證明,在雙交疊信號(hào)的情況下,IFM系統(tǒng)可能輸出信號(hào)1的頻率碼或信號(hào)2的頻率碼,也可能輸出與信號(hào)1和信號(hào)2都無(wú)關(guān)的頻率碼[1]。下面從理論上分析IFM對(duì)交疊信號(hào)的處理情況。
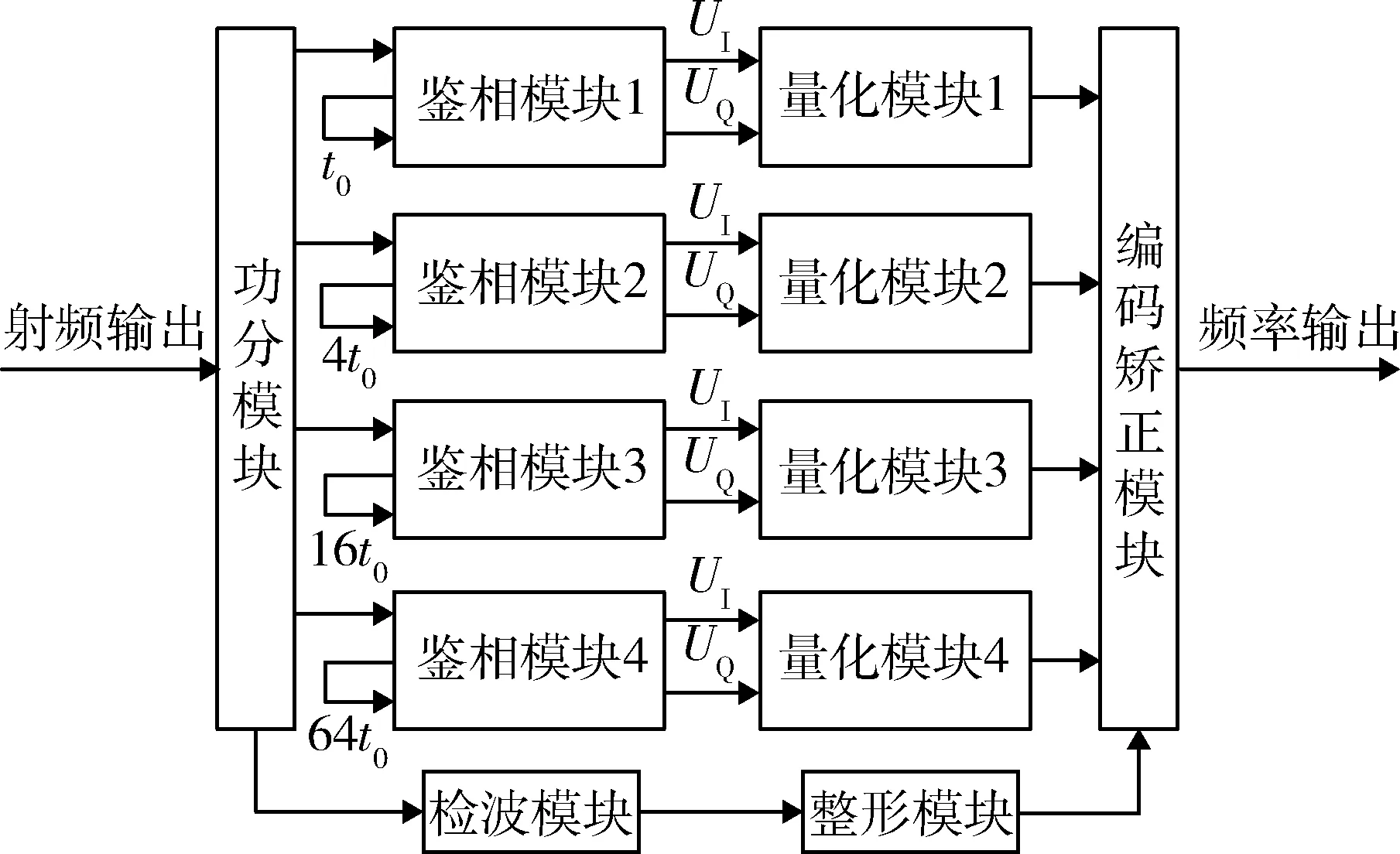
圖2 傳統(tǒng)IFM系統(tǒng)
2 交疊信號(hào)的IFM機(jī)理分析
2.1 脈沖交疊簡(jiǎn)介
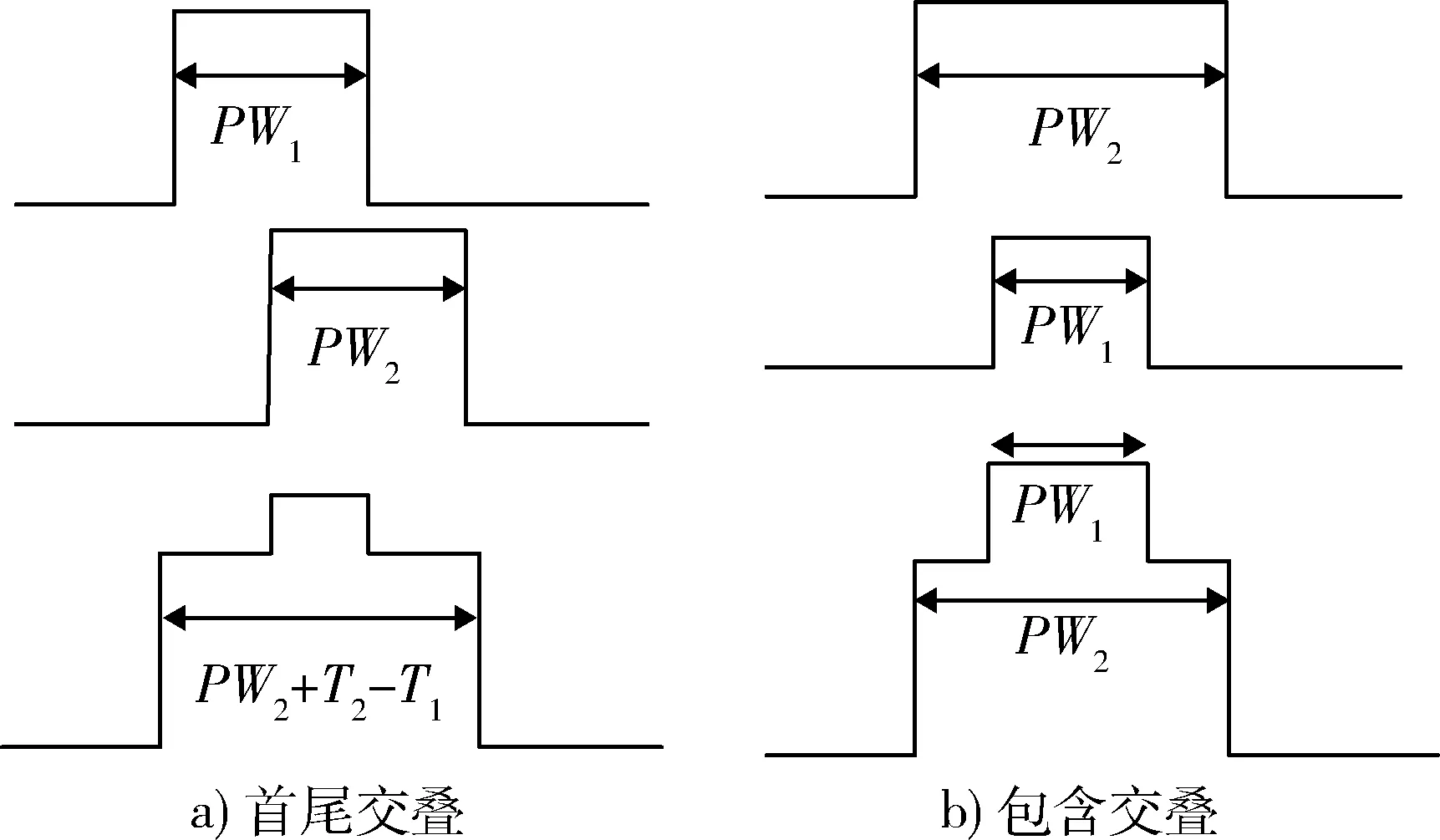
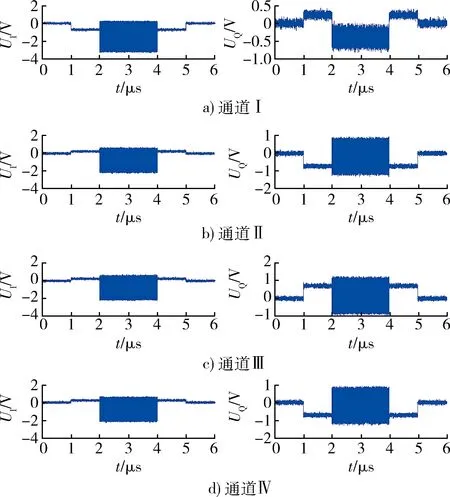
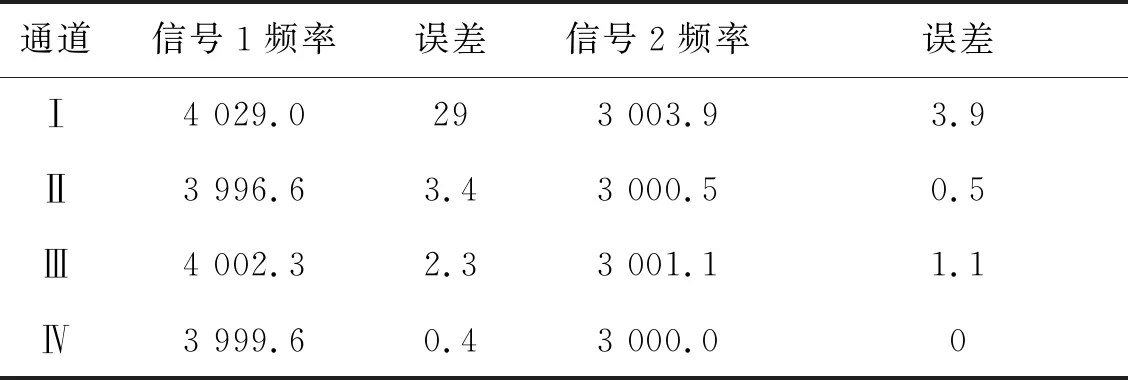
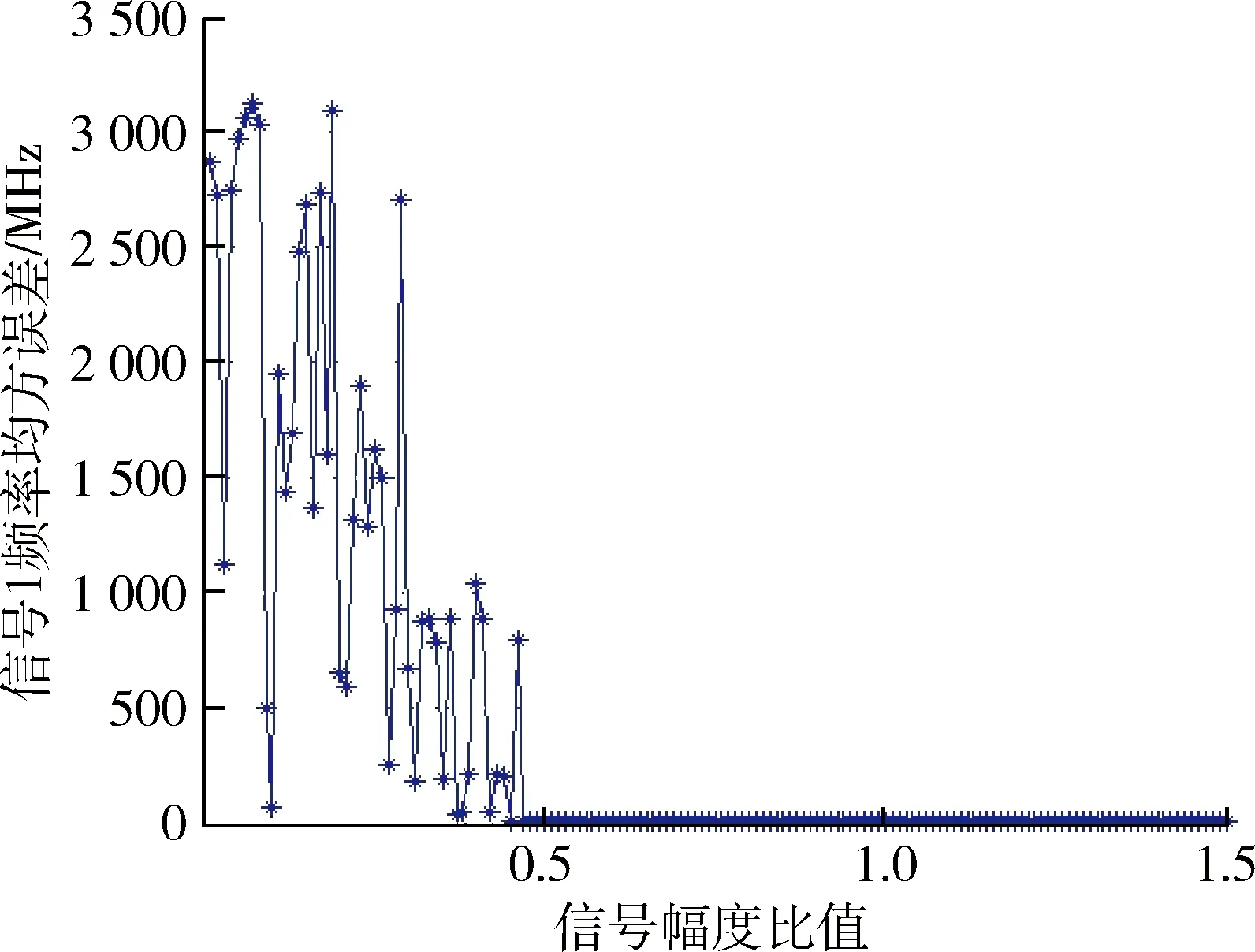
在復(fù)雜電磁環(huán)境下,由于IFM頻帶寬開,脈沖交疊不可避免。工程中2個(gè)脈沖完全交疊的概率是很小的[1],最基本的脈沖交疊是兩脈沖首尾交疊和包含交疊[13]。根據(jù)文獻(xiàn)[13],2個(gè)不同雷達(dá)脈沖到達(dá)時(shí)間分別為T1,T2,脈寬分別為PW1,PW2,當(dāng)滿足條件T1 出現(xiàn)多于2個(gè)脈沖交疊時(shí),雖然情況較復(fù)雜,但基本都可視為脈沖首尾交疊和包含交疊的組合。由于2個(gè)以上脈沖交疊的概率較小[3],故此后續(xù)內(nèi)容針對(duì)2個(gè)交疊信號(hào)作用于IFM系統(tǒng)進(jìn)行分析。 對(duì)于圖1所示微波鑒相器,若其輸入端同時(shí)存在2個(gè)信號(hào)如式(4)所示。 圖3 脈沖交疊圖 (4) 則根據(jù)微波鑒相器工作原理,端口1信號(hào)可表示為公式(5);端口2信號(hào)可表示為公式(6);端口3信號(hào)可表示為公式(7);端口4,5信號(hào)可表示為公式(8);端口6,7信號(hào)表示為公式(9);端口8,9,10,11信號(hào)可表示為公式(10);端口8,9,10,11經(jīng)過(guò)檢波器和差分放大器后,如2ω1,2ω2,ω1+ω2的高頻信號(hào)項(xiàng)被消掉,只剩直流和頻率為ω1-ω2的差頻信號(hào),則端口UI(t)可表示為公式(11);端口UQ(t)可表示為公式(12);公式(11),(12)不便于分析,對(duì)其做合理的公式代換,如公式(13)所示。 (5) U2(t)=A1cosω1t+A2cos(ω2t+φ), (6) U3(t)=A1cos(ω1t-φ1)+A2cos(ω2t+φ-φ2), (7) (8) (9) (10) UI(t)=K{[U9(t)]2-[U8(t)]2}= 4A1A2cos[(φ1+φ2)/2]cos[(ω1- ω2)t-(φ1-φ2+2φ)/2], (11) UQ(t)=K{[U11(t)]2-[U10(t)]2}= 4A1A2sin[(φ1-φ2+2φ)/2]· cos[(ω1-ω2)t-(φ1+φ2)/2], (12) (13) 式中:A1,A2分別為2個(gè)信號(hào)的幅度;ω1,ω2為2個(gè)信號(hào)的角頻率;φ為第2個(gè)信號(hào)的初始相位;φ1,φ2為2個(gè)信號(hào)經(jīng)過(guò)延遲線所產(chǎn)生的相移,φ1=ω1Δl/Cg1=2πf1T1,φ2=ω2Δl/Cg2=2πf2T2;Δl為延遲線長(zhǎng)度;Cg1,Cg2為延遲線中兩信號(hào)的傳播速度,工程中可近似相等。AI=4cos[(φ1+φ2)/2];AQ=4sin[(φ1-φ2+2φ)/2];φI=(φ1-φ2+2φ)/2,φQ=(φ1+φ2)/2。 需要指出的是公式(13)需要修正,這是由于差分放大器帶寬的限制。設(shè)差分放大器的帶寬為BWd,2個(gè)信號(hào)的頻差為ω1-ω2=Δω。當(dāng)Δω>>BWd時(shí),差頻分量全部被差分放大器濾除;當(dāng)Δω< (14) 工程實(shí)際中,BWd一般為幾十到幾百兆赫茲[14],而為了防止臨頻干擾,通常2個(gè)雷達(dá)信號(hào)的頻差Δω?BWd。在這種情況下,差頻分量被濾除,公式(14)修正為 (15) 對(duì)于圖3a)所示首尾交疊的情況,微波鑒相器的I,Q輸出值分為3個(gè)階段: 當(dāng)T1 (16) 當(dāng)T2 (17) 當(dāng)T1+PW1 (18) 對(duì)于圖3b)所示脈沖包含的情況,微波鑒相器的I,Q輸出值為:當(dāng)T2 由文獻(xiàn)[15]可知,可利用脈沖交疊部分的前后沿信息分離交疊信號(hào)。因此對(duì)于首尾交疊情況,根據(jù)T1 (19) 再由公式(3)估計(jì)信號(hào)1和信號(hào)2的頻率。 由以上分析可知,無(wú)論是脈沖首尾交疊,還是脈沖包含交疊,只要得到一個(gè)信號(hào)的UI,UQ,均可通過(guò)兩信號(hào)交疊區(qū)域的UI-12,UQ-12推算出另一個(gè)信號(hào)的UI,UQ,從而估計(jì)出2個(gè)交疊信號(hào)的頻率。但傳統(tǒng)的IFM接收機(jī)對(duì)一個(gè)脈沖信號(hào)只進(jìn)行一次采樣,無(wú)法進(jìn)行UI,UQ的推算,因此需作連續(xù)采樣。 綜上所述,UI,UQ推算法可歸結(jié)如下: (1) 用ADC(analog-to-digital converfer)模塊對(duì)4路微波鑒相器的輸出UI,UQ進(jìn)行連續(xù)采樣,得到離散電壓值。 (2) 根據(jù)檢波模塊、整形模塊輸出確定2個(gè)脈沖的交疊區(qū)和非交疊區(qū)。 (3) 計(jì)算模塊對(duì)交疊區(qū)和非交疊區(qū)的離散電壓取平均,應(yīng)用公式(3),(19)得2個(gè)信號(hào)的模糊頻率值。 (4) 計(jì)算模塊對(duì)4路輸出的頻率值作解模糊處理,得2個(gè)交疊信號(hào)的頻率估計(jì)值。 上述算法的第3和第4步在圖4框圖的數(shù)字解算中進(jìn)行。 圖4 UI,UQ推算法框圖 首尾交疊情況下,交疊前沿和后沿分別包含2個(gè)信號(hào)的頻率信息,可直接獲得,這里只仿真脈沖包含交疊的情況。 設(shè)IFM系統(tǒng)4路微波鑒相器延遲時(shí)間分別為0.15,0.6,2.4,9.6 ns,則頻率覆蓋范圍可達(dá)到2~6 GHz;差分放大器帶寬為10 MHz。對(duì)4路并行微波鑒相器的各個(gè)部件進(jìn)行仿真建模,為模擬實(shí)際情況,在仿真中對(duì)輸出加入信噪比為10 dB的噪聲。給輸入端饋入2個(gè)射頻脈沖信號(hào),這2個(gè)信號(hào)幅度分別為A1=1.2 V,A2=1 V;頻率f1=4 000 MHz,f2=3 000 MHz;脈沖寬度τ1=2 μs,τ2=4 μs。在其輸入端信號(hào)交疊情況如圖5所示。此信號(hào)經(jīng)過(guò)4路微波鑒相器后,若未考慮放大器帶寬BWd的情況下,可得如圖6所示4組UI,UQ值。 圖5 2個(gè)交疊信號(hào) 圖6 未考慮放大器帶寬的UI,UQ值 其中2~4 μs的交疊部分與公式(14)的分析比較吻合。考慮BWd之后,差分放大器將4組UI,UQ的差頻分量濾除,如圖7所示。再用ADC對(duì)其輸出的4組UI,UQ進(jìn)行連續(xù)量化采樣(設(shè)采樣頻率為16.7 MHz;量化間隔為0.187 5 V),所得100個(gè)離散電壓值如圖8所示。 圖7 濾波后的UI,UQ值 圖8 采樣量化后的UI,UQ值 由以上仿真可知,改進(jìn)后的IFM系統(tǒng)可以估計(jì)出2個(gè)交疊信號(hào)的頻率,但測(cè)頻精度受2個(gè)信號(hào)幅度的限制,為此作如下仿真: 表1 2個(gè)交疊信號(hào)的頻率值 設(shè)2個(gè)信號(hào)的幅度比K12=A1/A2,信號(hào)2的幅度不變A2=1 V,信號(hào)1的幅度從0 V變化至 1.5 V,每次增加0.01 V。根據(jù)蒙特卡羅定理進(jìn)行100次仿真,可得信號(hào)1的頻率均方誤差與2個(gè)信號(hào)幅度比的關(guān)系,如圖9所示。由圖9可知,2個(gè)信號(hào)的幅度比大于0.5時(shí),信號(hào)1的測(cè)頻誤差小于3 MHz;幅度比大于1時(shí),信號(hào)1的測(cè)頻誤差小于1 MHz。即信號(hào)幅度比大于0.5時(shí)可達(dá)到IFM精度要求。 圖9 誤差和幅度比的關(guān)系 由公式(14)可知,改進(jìn)后IFM系統(tǒng)的測(cè)頻精度受兩信號(hào)頻差和差分放大器的影響。設(shè)信號(hào)1的頻率f1由3 001 MHz增至3 020 MHz,每次增加0.1 MHz;信號(hào)2頻率f2=3 000 MHz,差分放大器帶寬BWd=10 MHz。仿真100次,可得信號(hào)1的頻率均方誤差與兩信號(hào)頻差的關(guān)系,如圖10所示。 圖10 誤差和頻差的關(guān)系 由圖10可知,當(dāng)兩信號(hào)的頻差遠(yuǎn)大于10 MHz時(shí),公式(14)中的差頻分量被差分放大器濾除,此時(shí)測(cè)頻精確,信號(hào)1的頻率誤差小于2 MHz;當(dāng)兩信號(hào)的頻差在10 MHz左右時(shí),公式(14)中的差頻分量部分通過(guò)差分放大器,此時(shí)交疊部分的差頻分量嚴(yán)重失真,信號(hào)1的測(cè)頻誤差很大;當(dāng)兩信號(hào)的頻差遠(yuǎn)小于10 MHz時(shí),公式(14)中的差頻分量全部通過(guò)差分放大器。由于對(duì)UI,UQ采樣值作時(shí)間平均處理,因此當(dāng)差頻分量是一個(gè)完整周期或一個(gè)完整周期倍數(shù)的信號(hào)時(shí),差頻分量被消除,此時(shí)測(cè)頻精確。其他情況下存在差頻分量,測(cè)頻誤差大。由此可知,當(dāng)兩信號(hào)頻差大于差放大器帶寬時(shí),新算法可精確地估計(jì)2個(gè)交疊信號(hào)的頻率。 由仿真驗(yàn)證和結(jié)果分析可得出如下結(jié)論: (1) 應(yīng)用UI,UQ推算法能夠估計(jì)雙交疊信號(hào)的頻率。 (2) 當(dāng)2個(gè)信號(hào)的幅度比相差不大時(shí),新算法具有較好的測(cè)頻精度。 (3) 由于差分放大器的帶寬不是很寬,所以新算法可處理在頻域上接近的交疊信號(hào)。 (4) 新算法沒(méi)有改變IFM的機(jī)理,因此依然具有瞬時(shí)帶寬寬、動(dòng)態(tài)范圍大的特點(diǎn)。 (5) 新算法在一個(gè)脈寬內(nèi)只采樣100個(gè)數(shù)據(jù),計(jì)算量小,運(yùn)算簡(jiǎn)單,因此具有較好的實(shí)時(shí)性。 本文推導(dǎo)了兩交疊信號(hào)經(jīng)過(guò)IFM系統(tǒng)后的理論輸出,建立了相應(yīng)的數(shù)學(xué)模型,并提出了一種估計(jì)交疊信號(hào)頻率的新算法—UI,UQ推算法,通過(guò)仿真驗(yàn)證了算法的有效性。本文的研究為今后IFM接收機(jī)的研制和改進(jìn)提供了一種新的思路,工程中便于實(shí)現(xiàn),有較好的實(shí)際應(yīng)用價(jià)值。若未來(lái)的IFM接收機(jī)能夠處理交疊信號(hào),將大大提升其在復(fù)雜電磁環(huán)境下的適應(yīng)能力。2.2 IFM脈沖交疊的理論分析
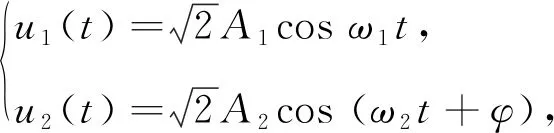
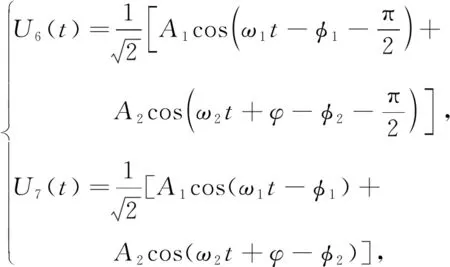
3 交疊信號(hào)頻率估計(jì)
3.1 交疊脈沖的I,Q通道輸出分析
3.2 UI,UQ推算法估計(jì)交疊信號(hào)的頻率

4 仿真校驗(yàn)及分析
4.1 微波鑒相器I,Q通道輸出仿真



4.2 修正模糊、估計(jì)交疊信號(hào)頻率
4.3 交疊信號(hào)幅度對(duì)測(cè)頻精度的影響
4.4 交疊信號(hào)頻率差對(duì)測(cè)頻精度的影響

4.5 仿真結(jié)論
5 結(jié)束語(yǔ)

