外涵氣流對內(nèi)涵氣流噪聲影響的數(shù)值研究

張正偉，劉亞楠，石飛云

(中國航發(fā)四川燃氣渦輪研究院，四川綿陽 621000)

1 引言

航空發(fā)動機噪聲中，噴流噪聲是最主要的噪聲源[1-2]，其對人體健康有重大危害，實際工程應用中需大幅降低。針對降低噴流噪聲這一難題，國內(nèi)外開展了大量的研究。研究認為，噴流噪聲功率與噴流速度的8次方成正比[3]，噴流噪聲抑制的關鍵是采取有效技術措施強化射流摻混[4]，降低射流和周圍大氣摻混的速度梯度[5]。速度梯度的大小反映了速度不一致的流體微團間剪切程度的強弱[6]，大的速度梯度的存在必然導致流體間的強剪切，使得噪聲源強度也隨之增加[7]。目前，主要的降噪措施有采用內(nèi)外涵波瓣混合器、鋸齒冠狀噴管混合器等。

本文提出一種降低噴流噪聲的方法，即在高速的內(nèi)涵射流外圍包裹一圈低速的外涵氣流，在降低內(nèi)涵氣流噪聲的同時，也增大了內(nèi)涵噪聲向外傳播的阻尼，從而使噪聲接收點的總聲壓級減小。研究中采用CFD/CAA方法，計算了外涵氣流參數(shù)對內(nèi)涵總聲壓級的影響規(guī)律，獲得了使內(nèi)涵總聲壓級最小的外涵氣流參數(shù)值。

2 計算方法與計算模型

在非穩(wěn)態(tài)CFD 流場的基礎上通過求解Ffowcs Williams-Hawhings(FW-H)方程，對聲源控制面或控制區(qū)域內(nèi)積分獲得某點的遠場噪聲是計算聲學的基本過程。本文的非穩(wěn)態(tài)流場采用大渦模擬方法對FW-H 方程進行數(shù)值模擬，其基本思想是對大尺度運動直接進行數(shù)值模擬，對小尺度運動做模型假設。大渦模擬的第一步是過濾掉小尺度脈動。濾波后的連續(xù)性方程和N-S方程可表示為[8]：

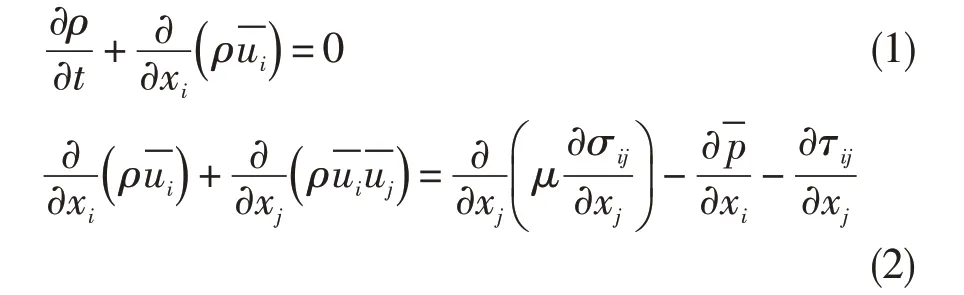
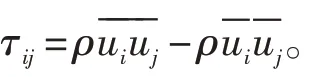
假定用各向同性濾波器過濾掉的小尺度脈動是局部平衡的，則可以采用渦黏形式的Smagorinsky亞格子雷諾應力模型求解亞格子應力[9]：

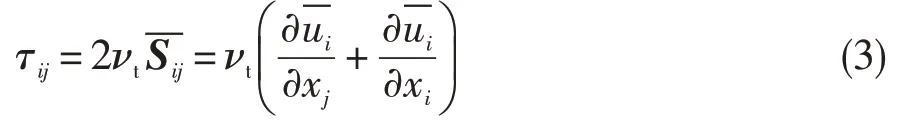
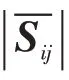
FW-H方程是利用廣義函數(shù)理論將連續(xù)性方程與N-S 方程重新整理為非均勻波動方程的形式[10]，可以寫成如下形式：

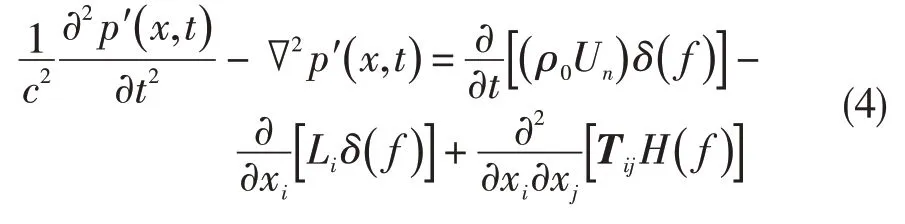
計算非穩(wěn)態(tài)流場的時間步長為0.000 005 s，每個時間步長內(nèi)迭代25 步，共計算10 000 個時間步長。計算模型如圖1所示，r為內(nèi)涵半徑，r+d為外涵半徑，d為外涵氣流層厚度。經(jīng)傅里葉變換，得到非穩(wěn)態(tài)湍流流場每個噪聲接收點的總聲壓級。噪聲接收點位于以氣流出口截面中心為圓心、半徑為5 m的圓周上，從-90°到90°，每間隔15°布1 個接收點，共13個接收點，如圖2所示。

圖1 計算模型示意圖Fig.1 Computational model

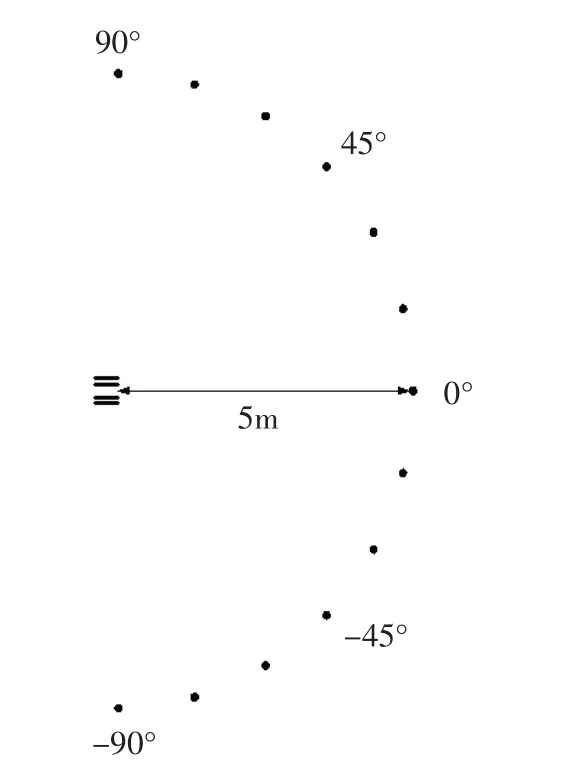
圖2 噪聲接收點位置示意圖Fig.2 The position of noise receiver

3 計算結果與討論

3.1 外涵氣流層厚度對噪聲屏蔽效果的影響

為了研究外涵氣流層厚度對噪聲屏蔽效果的影響，計算了相同內(nèi)涵半徑(50 mm)、不同外涵氣流層厚度(0，25，50，75 mm)的總聲壓級分布。表1給出了計算邊界條件。

表1 不同外涵氣流層厚度時的邊界條件Table 1 Boundary conditions of different bypass distances

圖3示出了不同外涵氣流層厚度時子午面的速度云圖。可看出，外涵氣流的存在增加了內(nèi)涵氣流射流核心區(qū)的范圍，且外涵氣流層厚度越大，內(nèi)涵氣流射流核心區(qū)的范圍就越大。

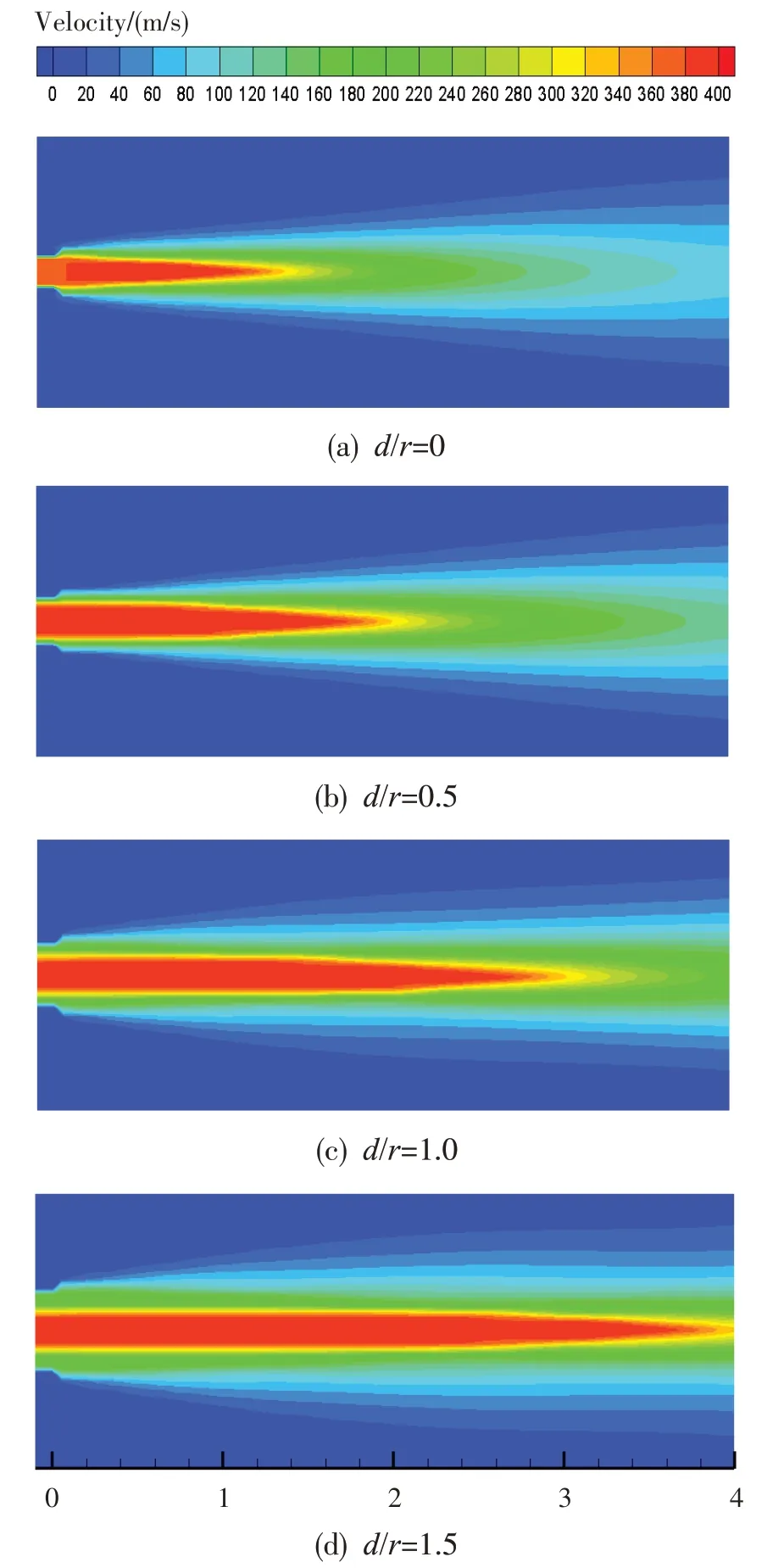
圖3 不同外涵氣流層厚度與內(nèi)涵半徑比時子午面速度云圖Fig.3 Velocity contour in symmetrical plane of different model

圖4示出了不同外涵氣流層厚度對總聲壓級的影響。可看出，無外涵氣流層(d/r=0)時，總聲壓級最大(0°位置)為145.1 dB；有外涵氣流層后，總聲壓級降低。d/r=0.5 時，總聲壓級最大(0°位置)為139.4 dB，減小了5.7dB；d/r=1.0 時，總聲壓級最大(0°位置)為135.9 dB，減小了9.2 dB；d/r=1.5 時，總聲壓級最大(0°位置)為145.6 dB，增大了0.5 dB。這表明并不是外涵氣流層厚度越厚總聲壓級的降低量就越大。就其原因，外涵氣流本身也是一個噪聲源，隨著外涵氣流層厚度增厚，射流核心區(qū)面積增大，與周圍大氣的摻混面積變大，產(chǎn)生的噪聲也越來越大，甚至超過了外涵氣流對內(nèi)涵氣流的屏蔽作用。此外，由圖還可知，其他條件相同時，不同角度位置的噪聲強度不同，0°位置總聲壓級最大，90°和-90°位置總聲壓級最小，相差18～24 dB。這可解釋為，無外涵氣流時，內(nèi)涵高馬赫數(shù)氣流直接與周圍大氣摻混，較高的速度梯度產(chǎn)生了強烈的噪聲。但在內(nèi)涵氣流與周圍大氣中加入外涵氣流后，內(nèi)涵氣流與外涵氣流較低的速度梯度產(chǎn)生低的摻混噪聲，速度梯度越小，噪聲越小；外涵氣流與周圍大氣較低的速度梯度產(chǎn)生了低的摻混噪聲。這兩部分的速度梯度小于內(nèi)涵氣流直接與周圍大氣混合的速度梯度。

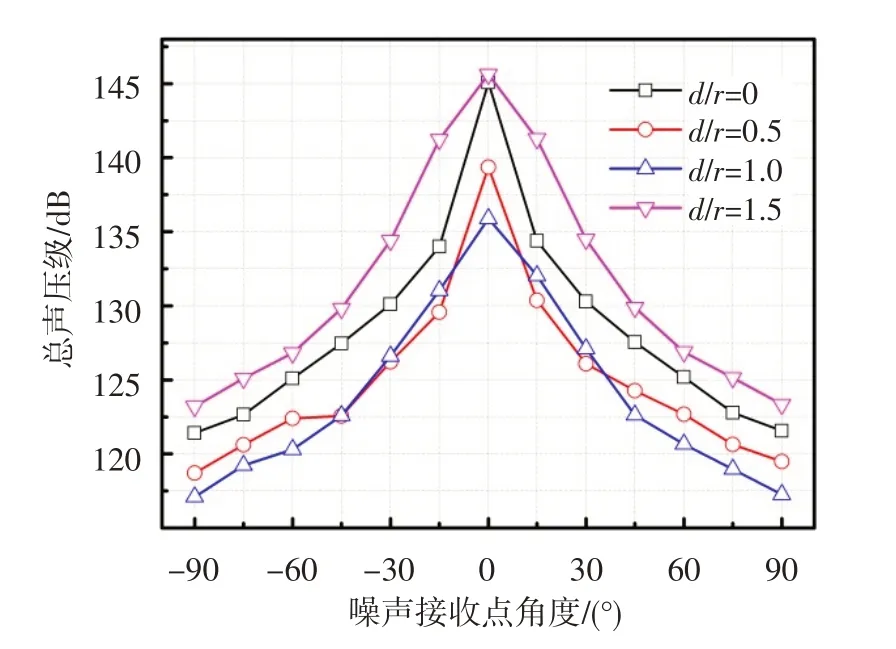
圖4 不同外涵氣流層厚度時的總聲壓級分布圖Fig.4 OASPL of different bypass distances

3.2 外涵氣流與內(nèi)涵氣流馬赫數(shù)之比對噪聲屏蔽效果的影響

內(nèi)涵氣流馬赫數(shù)Ma1為0.77、外涵氣流層厚度為100 mm(d/r=1.0)時，改變外涵氣流馬赫數(shù)Ma2，計算不同外涵氣流馬赫數(shù)對總聲壓級的影響。計算邊界條件如表2所示。

表2 不同內(nèi)外涵氣流馬赫數(shù)比時的邊界條件Table 2 Boundary conditions of different Mach number ratios

圖5給出了不同內(nèi)外涵氣流馬赫數(shù)比時各噪聲接收點的總聲壓級。由圖可知，當外涵氣流與內(nèi)涵氣流馬赫數(shù)之比為0.26，0.39，0.52，0.65時，總聲壓級最大值(0°位置)分別為136.0，133.5，132.7，135.9 dB，與無外涵氣流時的相比分別降低了9.1，11.6，12.4，9.2 dB。很顯然，本研究中，當外涵氣流馬赫數(shù)為內(nèi)涵氣流馬赫數(shù)的0.5倍時，能使內(nèi)涵氣流和外涵氣流的速度梯度以及外涵氣流與周圍大氣的速度梯度達到最小，噪聲源強度最小。

圖5 不同外涵氣流馬赫數(shù)時的總聲壓級分布圖Fig.5 OASPL of different bypass Mach numbers

3.3 外涵氣流與內(nèi)涵氣流總溫之比對噪聲屏蔽效果的影響

內(nèi)涵氣流馬赫數(shù)為0.77，外涵氣流馬赫數(shù)為0.50，外涵氣流層厚度為100 mm(d/r=1.0)時，改變外涵氣流總溫(T2)，計算不同氣流總溫比(T2/T1，T1為內(nèi)涵氣流總溫)對總聲壓級的影響。計算邊界條件如表3所示。

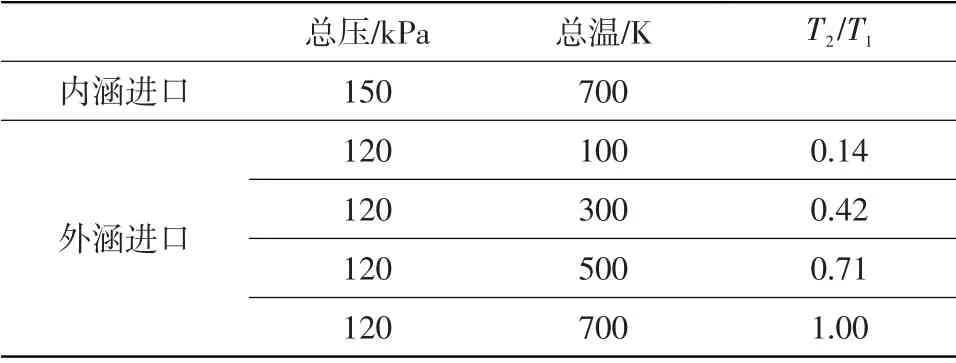
表3 不同內(nèi)外涵氣流總溫比時的邊界條件Table 3 Boundary conditions of different total temperature ratios

圖6給出了不同外涵氣流總溫時各噪聲接收點的總聲壓級。計算結果表明，外涵氣流總溫也是影響外涵氣流對內(nèi)涵噪聲源阻尼效果的關鍵因素。當外涵氣流與內(nèi)涵氣流總溫之比從0.14 增加到1.00時，0°位置總聲壓級先明顯減小再到略有減小，90°位置總聲壓級為略有減小到增大較多；0°位置總聲壓級分別為139.5，135.0，135.9，138.5 dB，90°位置總聲壓級分別為115.1，114.4，117.3，122.1 dB。外涵氣流與內(nèi)涵氣流總溫之比為0.42 時，噪聲接收點的總聲壓級最低，其中0°位置總聲壓級比無外涵氣流時的降低了10.1 dB。可解釋為，外涵氣流本身也是噪聲源，其總溫越高，噪聲強度越大。隨著外涵氣流總溫的升高，其對內(nèi)涵氣流噪聲的阻尼作用也增大。當外涵氣流總溫達到300 K(T2/T1=0.42)以上時，外涵氣流噪聲源的增大效果強于外涵氣流對內(nèi)涵氣流的阻尼效果，導致噪聲接收點的總聲壓級增大。當外涵氣流總溫為300 K(T2/T1=0.42)以下時，外涵氣流對內(nèi)涵氣流的阻尼效果大于外涵氣流噪聲源的增強效果，導致噪聲接收點的總聲壓級減小。外涵氣流總溫為300 K(T2/T1=0.42)時，噪聲接收點的總聲壓級最低。

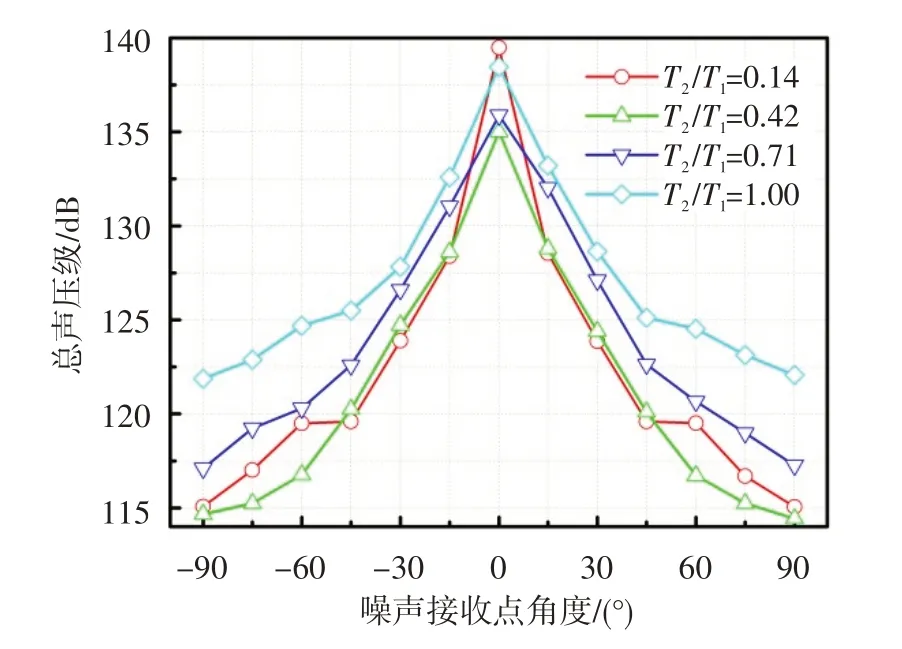
圖6 不同外涵氣流總溫時的總聲壓級分布圖Fig.6 OASPL of different bypass total temperatures

4 結論

利用CFD/CAA方法，研究了外涵氣流參數(shù)對內(nèi)涵氣流總聲壓級的影響，得出以下結論：

(1) 增大外涵氣流，內(nèi)涵氣流噪聲源強度減小，同時外涵氣流對內(nèi)涵氣流噪聲的阻尼作用增大，外涵氣流對內(nèi)涵氣流噪聲起到了屏蔽作用，噪聲接收點的總聲壓級降低。

(2) 隨外涵氣流層厚度增大，射流核心區(qū)范圍也增大。外涵氣流層厚度與內(nèi)涵氣流半徑之比為1.0 時，外涵氣流對內(nèi)涵氣流噪聲的屏蔽效果最好，噪聲接收點0°位置總聲壓級降低了9.2 dB。

(3) 外涵氣流與內(nèi)涵氣流馬赫數(shù)之比為0.52時，內(nèi)涵氣流與外涵氣流的速度梯度以及外涵氣流與周圍大氣的速度梯度達到最小，噪聲源強度最小，噪聲接收點0°位置總聲壓級降低了12.4 dB。

(4) 外涵氣流與內(nèi)涵氣流總溫之比為0.42且外涵氣流總溫為300 K 時噪聲接收點的總聲壓級最低，此時外涵氣流對內(nèi)涵氣流的阻尼效果大于外涵氣流噪聲源的增強效果。