概念構建 提升素養

摘 要：數學概念教學是數學思維培養、數學素養養成等教學目標實現的重要途徑;是學生扎實數學基礎知識和掌握基本技能的關鍵環節，是教學的核心之一，也是提升學生數學素養的第一要素，文章以指數函數概念和對數概念為例，深度展示概念課例的設計環節突破難點，由此提升數學素養。

關鍵詞：數學概念;指數函數;對數概念

新課程改革強調的數學教育的基本理念是學生發展為本、立德樹人、提升素養，特別指出在課堂教學過程中無情境不教學的理念。如何利用數學課堂教學既培養學生的數學基本知識和基本技能，又能提升學生的素養核心素養，在數學的概念教學時尤其要強調情境教學，教學思路為創設情境，提出問題，分析問題，解決問題。數學概念教學是數學思維培養、數學知識理解、數學素養養成等教學目標實現的重要途徑;數學概念教學是學生扎實數學基礎知識和掌握基本技能的關鍵環節，是教學的核心之一，也是提升學生數學素養的第一要素。縱觀數學發展史表明數學不只是邏輯推理，還有實驗;數學教育家波利亞認為：“數學有兩個側面，一方面數學是歐幾里得式的嚴謹科學，是一門系統的演繹科學，但另一方面，創造過程中的數學，看起來是一門試驗性的歸納科學。”隨著信息技術的發展，在課堂上可以融合信息技術進行數學實驗，培養學生的探究能力、數據分析和數學核心素養，以下以兩個數學概念教學案例具體說明。

課堂案例1 指數函數的概念

課程標準：能夠在熟悉的實際問題情境中，了解指數函數的實際背景，由具體到一般，抽象概括得出指數函數的概念。

活動1 設置問題情境、數據分析探路：

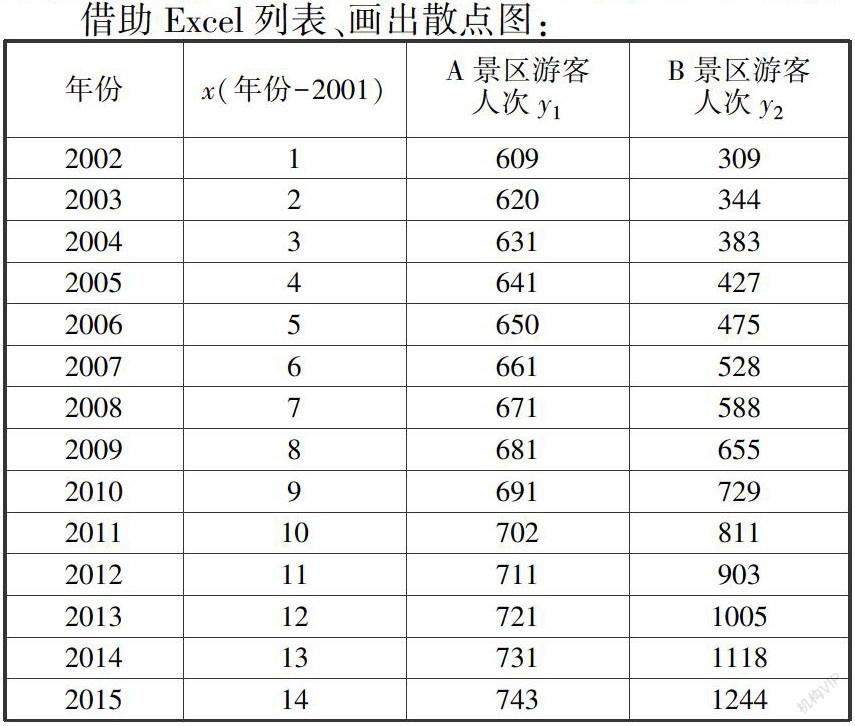
問題1 （2019人教A版必修第一冊P111）比較A、B兩地景區2002年-2015年的游客人次的變化情況，你發現了怎樣的變化規律？

研究問題的思路：通過實例創設情境，為指數函數的概念教學提供素材，回答了為什么要學習指數函數;接著提出如何研究實際問題的思路：提出問題、分析問題、解決問題;具體可以通過定性研究到定量研究，數據分析到圖像分析，研究變量之間的變化規律。

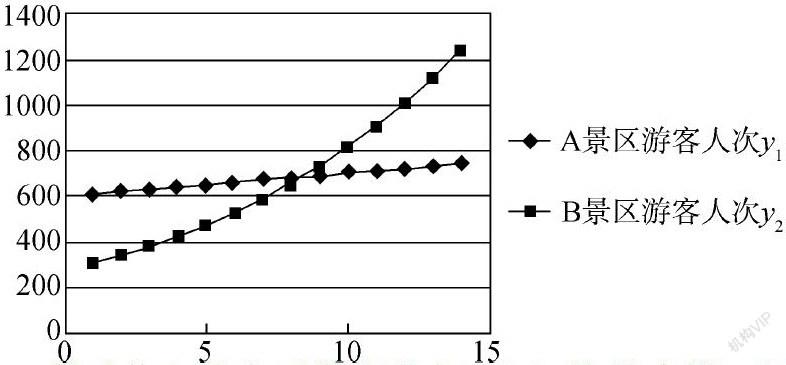
借助Excel列表、畫出散點圖：

借助信息技術對數據分析，進行數學建模，引導學生經歷圖表和圖像的形成過程，通過圖像概括變量間的變化情況，學會用自然語言描述：線性增長，非線性增長。B景區的游客人次近似于指數增長，增長率約為0.11。

活動2 從特殊到一般、數學抽象成型

分析從1年后，2年后，3年后的游客人次，從特殊到一般的思維過程，歸納出經過x年后的游客人次。

歸納得出經過x年后的游客人次函數關系式為：y=278×（1+0.11）x，其中指數x是自變量。

這個環節從問題情境中發現規律，提出猜想，進行探索，從特殊到一般的思維過程，且在運算過程進行詳細的分解，最后歸納得一般的結論，符合高一學生思維的最近發展區。布魯納指出：學生不是知識的接受者，而是積極的信息加工者。在這一環節中，教師通過引導，培養學生的數學運算能力和歸納推理能力，同時通過分解難點，建立分析問題的模板，提升學生學習數學應用題的信心。

活動3 構建指數函數、深化概念教學

問題2的函數關系研究思路類比問題1的活動2的過程可得生物死亡年數x與死亡生物體內碳14含量y的函數關系：

著名教育家夸美紐斯認為：如果不先教明概念，便是教的不好。根據認知心理學，概念辨析是獲得概念的必須步驟，通過具體實例進一步理解概念的內涵與外延。因此在這一環節中，對指數函數的概念進行以下幾個方面進行深化探究：

活動4 總結研究思路、提升數學素養

引導學生對研究指數函數的概念的學習過程進行自主小結，可以利用思維導圖;也可以問題串式小組進行討論總結。比如問題串式：通過這節課的學習，用哪些研究方法？研究指數函數的基本思路是什么？你感受到了什么數學思想或者心得體會？小結的目的是引導學生學會做中學數學，學會數學化的學習，學會合作學習與交流，提升數學素養。

課堂案例2 對數的概念

活動1 回歸初心、問題辨析

16世紀，天文學蓬勃發展，天文學家們每天要面對大量煩瑣的計算，如兩個較大數的連乘，比如：512×16384=？

問1：請同學們不借助計算器，能否快速得出結果？接著展示下列表格：

問2：借助表格數據，能否找到簡化上述式子求解過程的方法？

因為512=29，16384=214，因此512×16384=29×214=29+14=223=8388608，

問題化歸為把因數寫成同底的指數冪的形式，轉化為求指數數值的和即可。

問3：一般化，512×16384=2m×2n，求解m，n值。

問4：更一般化，512×16384=10m×10n，求解m，n值。

問5：方程512=10m是否有解？有幾個解？如何表示？

著名數學家丁石孫曾說：“沒有問題的學生不能算好學生。”問題是創新的基石。這個環節從數學發展史引入，問題設置接近學生的“最近發展區”，情境材料具有探究性和趣味性，有利于學生的觀察、實驗、猜想、推理與交流等，讓學生的心理激發認知的沖突，從而產生問題意識，促進探究學習，回答了為什么要學習新知識對數的概念。

活動2 數形結合、探究求解

借助《幾何畫板》軟件探究方程512=10m的解問題，讓學生有更直觀的認識。為了畫圖探究的方便設置先探究方程

如圖點A的橫坐標即方程2x=3的解，存在且唯一;同理方程512=10m的解存在且唯一。

本環節利用信息技術融合輔助教學，創設逼真的教學情境，直觀展示問題的解，化抽象為直觀，數形結合思想的滲透，提升學生的數學抽象與直觀想象素養，充分調動學生的學習積極性。

活動3 溫故知新、類比推廣

問1：方程2x=3解如何表示？

這個方程的解的表示超出已有的知識范圍，所以需要引入符號。教師引導回顧以前在學習解方程，當遇到解超出數表示范圍是的情況：

問2：將對數的概念一般化？

這個環節對于對數符號的引入以溫故知新的形式產生，自然又不失單調，有類比推理，又為后面的對數式與指數式的化簡運算作鋪墊，學生的認知也不會太突然，有符合學生認知的“最近發展區”。由對數的概念可知，對數與指數密切相關。這是數學家歐拉在1770年出版的一部著作中首先使用log符號并指出“對數源于指數”。然而對數的發明先于指數，對數是蘇格蘭數學家納皮爾于1614年出版《奇妙的對數定律說明書》標志著對數的誕生。

數學家哈爾斯曾指出：“問題是數學的心臟”，數學基本概念的教學需要教師進行深度的挖掘，設置層層問題情境，讓學生把數學概念轉化為自己的概念，教師在整個教學過程起引導作用，創設概念的產生和發展過程的問題鏈，讓學生自主或以主體作用體會數學概念的形成，教師的引是關鍵，數學的探是主體，二者相輔相成。數學核心素養的養成需要一個過程，平時教師在教學過程中需要不定時地引導滲透，根據不同數學概念內容，教師一定要靈活設計，潛移默化的滲透數學核心素養，通過數學概念課學習，讓學生構建數學概念、提升數學素養。

參考文獻：

[1]課程教材研究所，中學數學課程教材研究開發中心.普通高中教科書（A版）：數學（必修第一冊）[M].北京：人民教育出版社，2020.

[2]涂榮豹，寧連華.中學數學經典教學方法[M].福州：福建教育出版社，2011.

[3]杜美英.數學概念教學探析[J].數學之友，2020（1）.

作者簡介：劉英得，福建省廈門市，福建省廈門市杏南中學。