非對稱循環載荷下Q235鋼力學響應特性分析

張慶玲，金淼，李群，郭寶峰

(1.燕山大學 先進鍛壓成形技術與科學教育部重點實驗室，河北 秦皇島 066004；2.燕山大學 機械工程學院，河北 秦皇島 066004)

工程中的承載結構在工作中常由于載荷或幾何形狀不連續而產生應力集中，甚至會在局部出現塑性變形。此時，對于受循環載荷作用的結構件則可能出現棘輪效應、包申格效應、循環軟/硬化等變形行為，從而影響結構性能。因此，深入了解材料在循環載荷作用下的力學相應特性對于結構設計及安全評定具有十分重要的意義。棘輪應變會隨著循環次數的增加而增加，會嚴重惡化部件的性能[1]。棘輪應變的累積取決于載荷中平均應力和應力幅值的組合[2-3]。在恒平均應力時，無論應力速率如何變化，隨應力幅值的增加，棘輪壽命都會下降，棘輪應變累積率增加[4-6]。這些研究使人們對金屬材料棘輪效應的基本特性有了較為深入的了解。

包申格效應是指金屬材料在經歷了一定量的單向拉伸或壓縮塑性變形之后再反向加載，其屈服應力會低于連續正向變形的屈服應力，這是造成金屬材料力學方向性的重要原因之一[7-9]。盛光敏等[10]通過對AZ31進行拉壓和壓拉循環試驗，得出其包申格效應比反包申格效應明顯；文獻[11-12]分析了不同應變歷史、預應變量、應變速率和循環周次對鋁合金7A04和高強鋼10CrNi5MoV包申格效應的影響；文獻[13-14]對Q345、Q460和Q235進行循環加載試驗，指出3種鋼材均存在包申格效應。

當外加循環載荷使得材料進入塑性變形后，反復變形會令金屬的塑性流動特性發生變化，造成材料抵抗變形的能力增強或減弱，這種現象稱為循環硬化或循環軟化。文獻[15]探討了不同加載條件下不銹鋼316L的循環軟硬化行為；文獻[16-18]指出低碳鋼S355循環硬/化行為隨塑性應變范圍的增大而增大，循環軟化行為隨塑性應變范圍的減小而減小；文獻[19-21]研究發現Q235鋼在不同應變幅值和平均應變組合下表現為循環硬化，循環硬化指數隨平均應變水平的增加而增大。

學者們對不同材料在不同條件下的循環變形特性進行了深入探討，但對于焊接結構件最為常用的Q235鋼在非對稱應力控制下產生棘輪效應、包申格效應及循環軟硬化特性的系統研究卻鮮見報道。本文以Q235鋼為研究對象，進行了多種條件下的循環加載試驗，運用數據分析的方法，并結合唯象理論，對試驗結果進行系統分析，深入研究了此材料的力學響應特性。

1 應力循環加載試驗方案

試驗所用原材料為20 mm厚Q235鋼板，測得其彈性模量為210 GPa，上、下屈服極限分別為310 MPa和243 MPa。沿軋制方向取樣，按照GB/T 3075-2008《金屬材料疲勞試驗軸向力控制方法》加工成圓形截面循環加載試樣，其平行段直徑9 mm，平行段長度27 mm，過渡圓弧半徑25 mm。在精度為0.2 kN的Instron8801型電液伺服疲勞試驗機上進行循環加載試驗，并通過精度為0.1 μm，標距為25 mm的接觸式引伸計采集軸向應變。試驗加載波形如圖1所示，加載應力率為40 MPa/s，循環周次為30周，具體試驗方案如表1所示。

表1 應力循環試驗加載工況Table 1 Loading conditions of stress cycle test

圖1 應力循環加載曲線Fig.1 Single stage stress cyclic loading curves

2 棘輪效應分析

本文材料在非對稱應力循環載荷作用下產生的棘輪應變εr為：

(1)

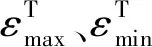
由于Q235鋼存在屈服平臺，使得第1周的應變值較大，棘輪應變的計算均從第2周開始。將相鄰2個循環周次內棘輪應變的變化量定義為棘輪應變率Δεr，其反映了循環加載過程中棘輪應變累積的快慢程度。

應力幅值為300 MPa，平均應力分別為-20 MPa和20 MPa時，循環加載過程中Q235鋼的應力應變曲線如圖2所示。可以看出，正、負平均應力時均產生了棘輪效應。當平均應力為負值時，隨循環周次的增加，滯回曲線向負應變方向移動；當平均應力為正值時，滯回曲線則向正應變方向移動。

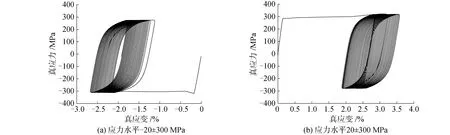
圖2 循環應力應變曲線Fig.2 Cyclic stress-strain curve

應力幅值為300 MPa，不同平均應力條件下棘輪應變隨循環周次的變化如圖3所示。由圖可知，平均應力為正值時棘輪應變為正值，平均應力為負值時棘輪應變為負值，棘輪應變的絕對值均隨循環周次增加而增大。不同正負平均應力條件下棘輪應變的變化趨勢不同，且棘輪應變率也不相同，但棘輪應變率均在第20周后趨于穩定。

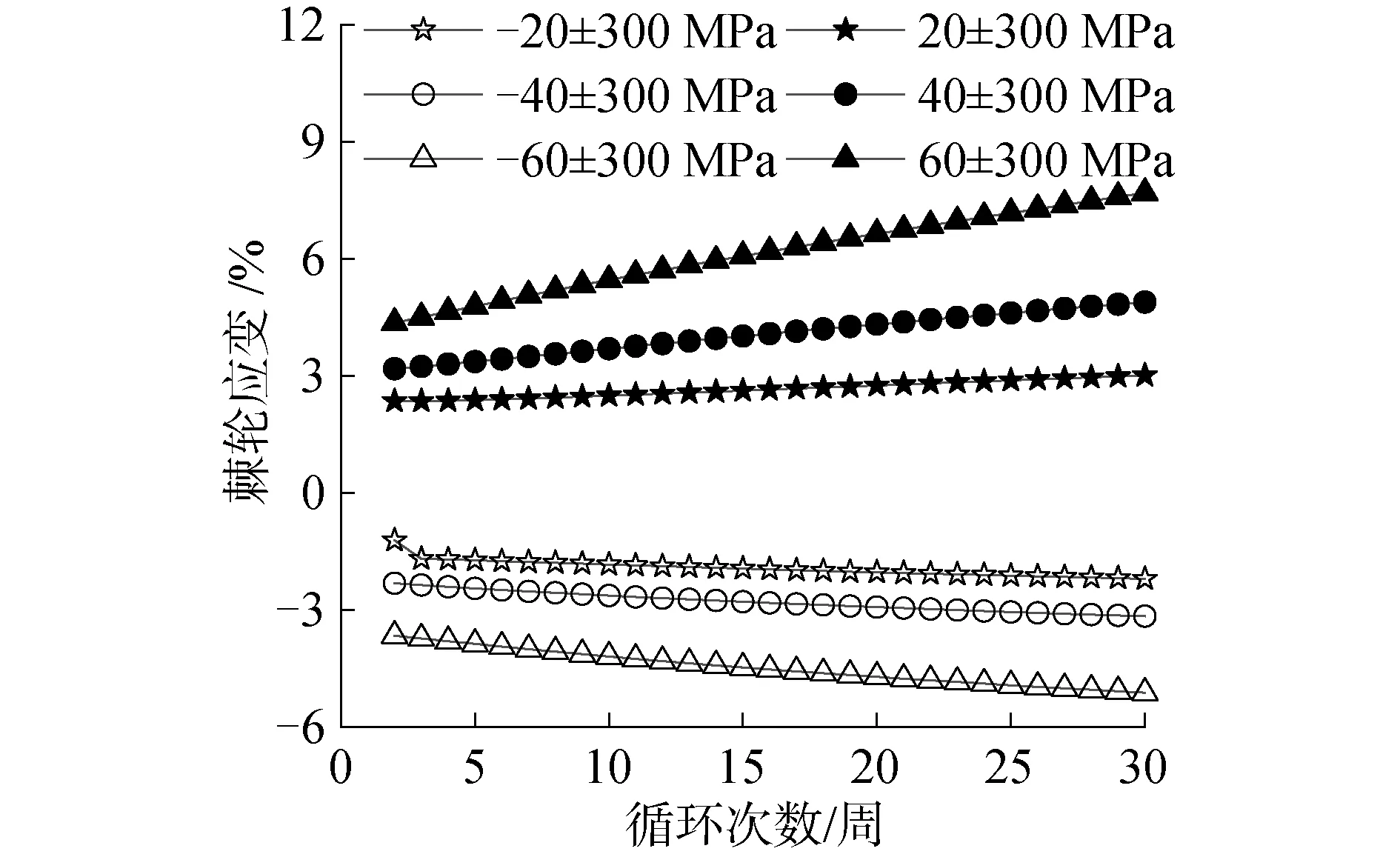
圖3 應力幅值為300 MPa時的棘輪應變Fig.3 Ratcheting strain at stress amplitude 300 MPa

平均應力為正值時，棘輪應變率為正值，平均應力越大，棘輪應變率越高；平均應力為負值時，棘輪應變率為負值，平均應力絕對值越大，棘輪應變率也越高。應力幅值為300 MPa時，棘輪應變率穩定值與平均應力之間的關系曲線如圖4所示，兩者之間呈指數函數關系。

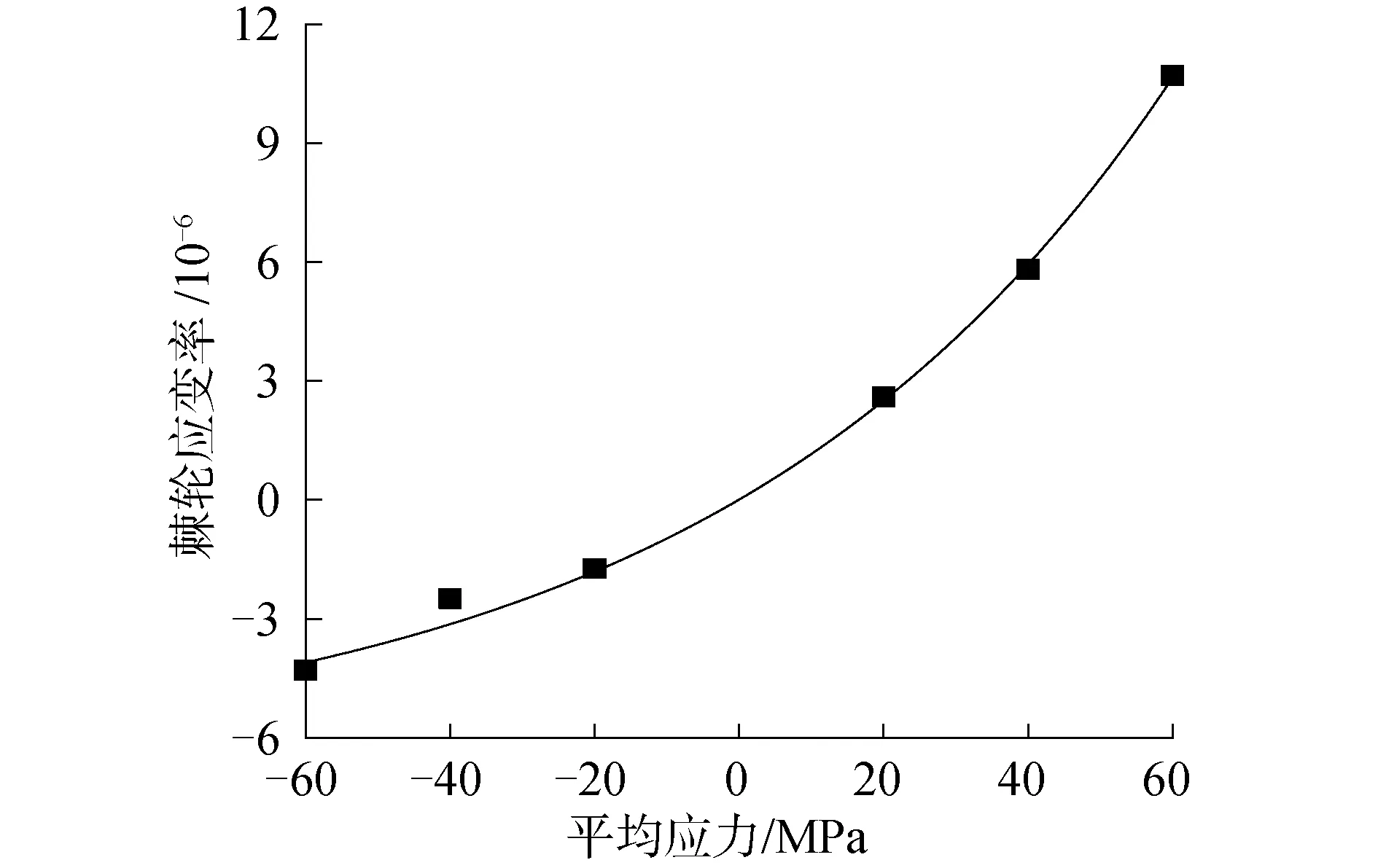
圖4 應力幅值為300 MPa時不同平均應力下的棘輪應變率Fig.4 Ratcheting strain rate under different mean stress at stress amplitude 300 MPa

圖5所示為不同應力幅值下Q235鋼的棘輪應變曲線。無論平均應力為正值還是負值，棘輪應變及棘輪應變速率均隨應力幅值的增加而增大。

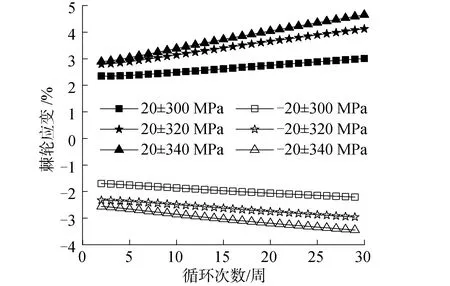
圖5 不同應力幅值條件下的棘輪應變Fig.5 Ratcheting strain at different stress amplitude

由上述分析可知，Q235鋼在循環過程中產生的棘輪應變與平均應力、應力幅值和循環周次有關，根據唯象理論得出棘輪應變的預測模型：

(2)

式中：λ為材料參數，可通過試驗數據獲取，此處取λ=3.5；N為循環周次；σm為平均應力；σa為應力幅值；σ′s0、σs0分別為單向拉伸時的上、下屈服極限；η=σa/σs；ε′為循環加載試驗時應力峰值在單向拉伸試驗曲線中所對應的應變值。

如圖6所示，將計算得到的棘輪應變與試驗數據進行對比，兩者吻合良好，說明該公式可以在非對稱應力控制的循環加載試驗中，較好的表征Q235鋼的棘輪效應。

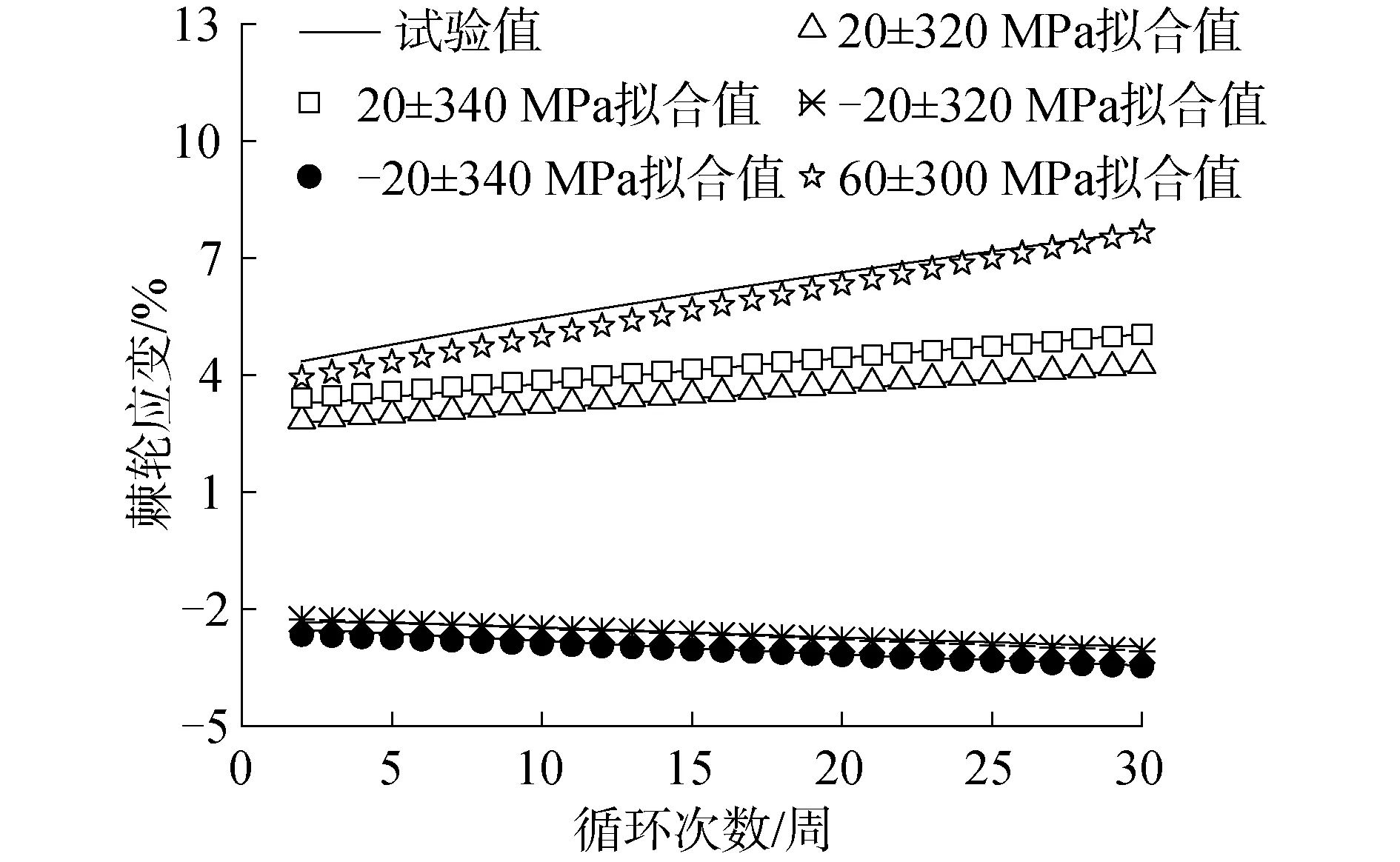
圖6 棘輪應變試驗值與擬合值比較Fig.6 Comparison of test and fitting data of ratcheting stress

3 包申格效應分析

包申格效應在金屬材料構件中一般扮演著負面的角色，會影響到材料的抗疲勞性能，造成工件不能滿足正常的服役條件。試驗發現，Q235鋼在循環加載過程中產生了明顯的包申格效應。為使計算結果更有可比性，在循環第1周取屈服平臺的值作為屈服應力，其他不產生屈服平臺且無明顯屈服點的循環周次，取相應周次發生0.2%相對塑性變形時對應的應力值，即取該周應力應變曲線起始部分的斜率，然后偏移0.2%應變量對應得到的應力值。

圖7給出了應力幅值為300 MPa，不同平均應力條件下的屈服應力隨循環周次的變化曲線。圖中顯示，當平均應力為負值時，壓縮屈服應力大于拉伸屈服應力，平均應力絕對值越大，拉伸屈服應力越小，壓縮屈服應力越大；而當平均應力為正值時，拉伸屈服應力大于壓縮屈服應力，平均應力越大，拉伸屈服應力越大，壓縮屈服應力越小。且隨循環周次的增加無論平均應力為正值還是負值，拉伸和壓縮方向的屈服應力均呈現下降趨勢。

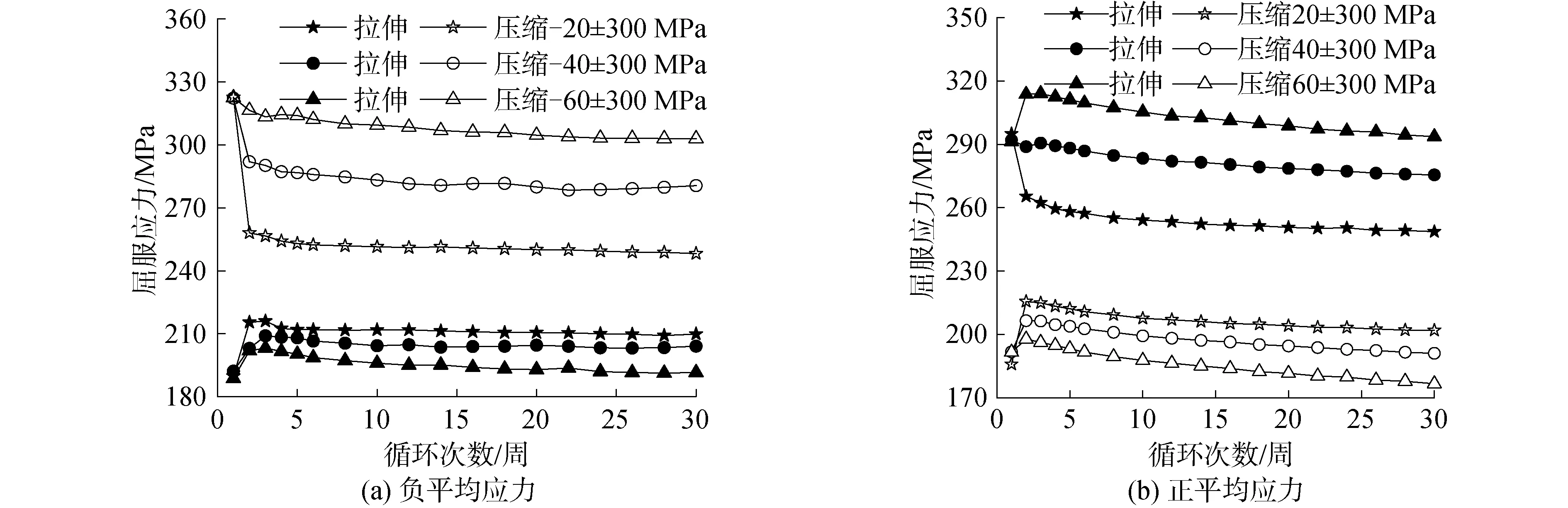
圖7 不同平均應力條件下屈服應力隨循環周次變化曲線Fig.7 Changing curves of yield stress with cycle numbers at different mean stresses

圖8為相同平均應力不同幅值條件下各循環周次的屈服應力。結合圖7的結論，可以得出，在應力載荷控制下，在拉伸和壓縮2個方向哪個方向載荷大，對應方向的屈服應力相對較高。平均應力一定時，隨應力幅值的增大，拉伸屈服應力和壓縮屈服應力均略有增大，在循環到第30周時相鄰載荷條件下的屈服應力相對變化量不超過2%。對比圖7和圖8，可以看出，平均應力和應力幅值分別增大所得到的屈服應力變化規律并不一致，相同峰值條件下，平均應力比應力幅值對屈服應力的影響更為明顯。這是因為，平均應力為負值時，平均應力增大，應力峰值減小，應力谷值絕對值增大；平均應力為正值時，平均應力增大，應力峰值增大，應力谷值絕對值減小；而應力幅值增大，正負平均應力下的應力峰值和應力谷值的絕對值均增大。

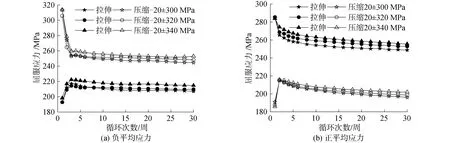
圖8 不同應力幅值下的屈服應力變化曲線Fig.8 Changing curve of yield stress at different stress amplitude and same mean stresses

從上述對屈服應力的數據分析可以得出，屈服應力是關于循環周次、平均應力和應力幅值的函數。當外加載荷大于上屈服極限時，屈服應力σs隨循環周次的演化規律為：

(3)

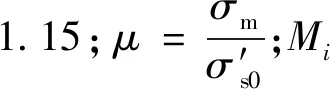
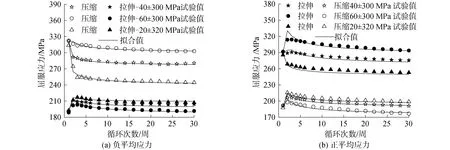
圖9 屈服應力試驗值與擬合值比較Fig.9 Comparison of test data and fitting data about yield stress

包申格系數B與循環載荷作用下預拉伸/壓縮變形后屈服應力的變化直接相關，可對包申格效應進行定量表征和描述，其表達式為：

(4)

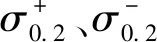
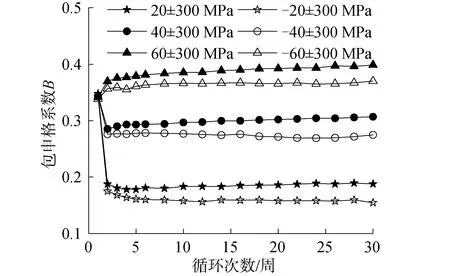
圖10 應力幅值為300 MPa時包申格系數隨循環周次的變化Fig.10 The variation of Bauschinger coefficient with cycle numbers at stress amplitude 300 MPa

可以看出，不同應力狀態第1周時的包申格系數基本相同，約為0.346，說明Q235在經歷一定的預拉伸/壓縮變形后再反向壓縮/拉伸時均表現出明顯的包申格效應。從第2周開始，包申格系數隨平均應力的變化表現出較大差異，但相同應力條件下則變化很小。因此，可以用第2周的包申格系數來描述材料的包申格效應。平均應力絕對值越大，包申格效應越顯著。平均應力絕對值相同時，Q235鋼在正平均應力條件下表現出的包申格效應更明顯。

4 循環軟/硬化特性分析

Q235鋼在不同應力組合條件下表現出不同的循環軟/硬化行為。不同平均應力和應力幅值條件下的響應應變幅值隨著循環周次的變化曲線如圖11所示。可以看出，當平均應力為負值時，表現出輕微的硬化特性；當平均應力為正值時，則表現出明顯的軟化特性，但2種工況下，應力幅值越大應變幅值越大，而平均應力絕對值越大應變幅值卻越小。隨循環周次的增加，Q235鋼循環軟/硬化速率在第20周之后趨于穩定。將不同應力條件下的循環軟/硬化速率穩定值列于表2，負值表示循環硬化，正值表示循環軟化。

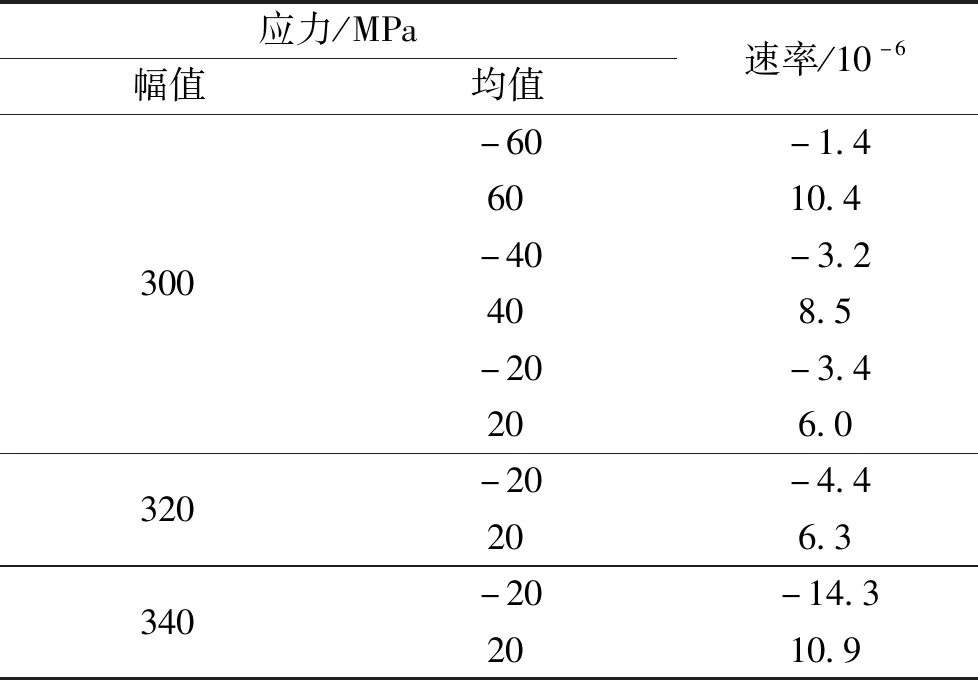
表2 不同條件下的循環軟/硬化速率Table 2 Cyclic softening/hardening rate at different conditions

圖11 不同條件下的應變幅值變化曲線Fig.11 Changing curve of strain amplitude at different conditions

比較發現，負平均應力時，循環硬化速率隨平均應力絕對值的增大逐漸減小，即硬化程度減弱；正平均應力時，循環軟化速率隨平均應力的增大呈增長趨勢，即軟化程度增強；應力幅值增大使循環軟硬化速率均增加，軟硬化程度更顯著。

5 結論

1) 在非對稱應力循環載荷作用下，負平均應力產生負棘輪應變，正平均應力產生正棘輪應變。

2) 外加載荷平均應力相同，應力幅值增大，或外加載荷應力幅值相同，平均應力絕對值增大，均會造成棘輪應變絕對值增大，棘輪應變率升高。

3) 在非對稱應力循環載荷作用下，Q235鋼表現出明顯的包申格效應。當平均應力為負值時，壓縮屈服應力大于拉伸屈服應力；當平均應力為正值時，拉伸屈服應力大于壓縮屈服應力。在循環的第1周屈服應力值基本相同，可以用第2周的包申格系數來表征材料的包申格效應。

4) 當外加載荷平均應力為負值時，Q235鋼表現出循環硬化特性，平均應力絕對值越小或應力幅值越大，循環硬化現象越明顯；當外加載荷平均應力為正值時，Q235鋼表現出循環軟化特性，平均應力或應力幅值越大，循環軟化現象越明顯。