水槽邊壁效應對四柱結構準陷波現象的影響

紀翀，杜一豪，姜勝超

(1.大連理工大學 船舶工程學院，遼寧 大連 116024;2.大連理工大學 海岸和近海工程國家重點實驗室，遼寧 大連 116024)

近些年，海上資源開采逐漸向深海發展，浮式海洋平臺逐漸受到了越來越廣泛的關注，這些平臺通常由多根大直徑立柱組成，在某些惡劣海況下，波浪上涌對平臺下甲板產生沖擊，產生較大的作用力與傾覆力矩。因此，充分考慮波浪作用下立柱作用力及附近自由水面變化是浮式海洋平臺設計的關鍵。目前在波浪干涉現象領域已經有了大量研究，Maniar等[1]對100根直線排列的圓柱的波浪力進行了研究，發現在某一頻率作用下，圓柱所受波浪力顯著增大，出現類似準陷波的現象。Evans等[2]研究了波浪作用下柱群內部產生的一階準陷波現象，并發現準陷波現象發生頻率與結構的尺寸和布置形式密切相關，且發現時的波面分布具有明顯的對稱與反對稱特征。OHL等[3-4]對規則波和不規則波作用下張力腿平臺附近的波浪場變化進行研究。通過數值結果與實驗資料的對比，發現通過線性繞射理論獲得的數值計算結果和實際情況較為擬合。然而，該工作并沒有對復雜的準陷波現象開展深入的研究。文獻[5-9]對多柱結構準陷波現象展開了更加深入的研究工作。在水槽中圓柱體繞射研究領域中，Ursell[9]和Masashi[10]分別提出了高效求解圓柱體的二維繞射問題和將水槽中的格林函數分解的方法。Bennet等[11]提出了基于波長遠小于水槽寬度的平面波近似方法，可以求解任意形狀的軸對稱體。寧德志[12]將快速多極子展開的方法用于水波問題的計算，基于非線性時域理論，對數值波浪水槽中圓柱周圍波面與波浪載荷計算結果與開敞海域進行對比。趙一帆[13]采用源匯分布法，以滿足水槽邊壁條件的格林函數建立了數值模型，以水槽中座底且穿透水面的等截面柱體為研究對象，并利用波能流守恒關系驗證了計算方法的正確性。

在對多柱結構周圍波面分布的研究中，通常會采用模型實驗的方法，而模型試驗往往在水槽中間進行。為了探究邊壁效應對準陷波現象的影響，本文基于理想流體假設的勢流理論，借助水動力計算軟件HydroStar對三維圓柱狀浮體的波浪繞射進行分析，研究勢流對波浪與四柱結構相互作用問題，分別對有無邊壁水槽時四柱結構周圍波面特征進行對比，并著重分析了圓柱半徑對準陷波現象的影響規律。

1 勢流理論與常數元方法

在理想不可壓縮流體且運動無旋假設下，流體運動存在速度勢Φ(x,t)，其滿足拉普拉斯方程為：

2Φ(x,t)=0

(1)

波陡ε為：

ε=kA

(2)

式中：k為波數；A為波幅。

對速度勢Φ(x,t)按ε進行攝動展開，取一階近似。當入射波頻率為ω時，將時間因子e-iωt分離，從而變為：

Φ(x,t)=Re[φ(x)e-iωt]

(3)

式中：φ為空間復速度勢，仍然滿足拉普拉斯方程。對于固定不動的物體，可以將空間復速度勢進一步分解為入射勢φi與繞射勢φd，其中，繞射勢φd應滿足自由水面、物面、水底、無窮遠以及水槽側壁邊界條件。

取能同時滿足條件的格林函數G(x,x0)，并對其與繞射勢應用第二格林定理，采用常數元方法進行離散，可建立積分方程為：

(4)

式中n為物面法向量(以指出流體為正)。

開敞水域的情況，采用John推導的滿足自由水面邊界條件格林函數的形式為：

(5)

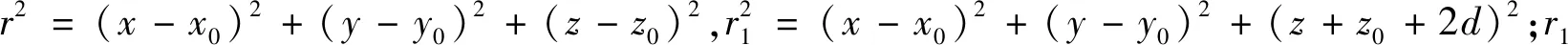
對于考慮水槽邊壁時的情況，采用源像法消除水槽側壁積分[13]，引入水槽格林函數為：

(6)

式中：αm=(m2π2-k2W2)1/2=-i(m2π2-k2W2)1/2；εm是諾依曼符號：ε0=1；εm=2，m≥1;W是水槽寬度。

對于規則波入射的情況，波面為：

ζ=Re[η(x,y)e-iωt]

(7)

其中：

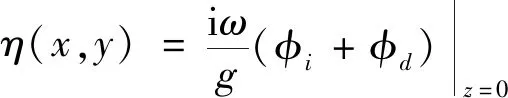
(8)

式中：g為重力加速度，繞射勢φd可通過下述方程求出：

(9)

2 數值試驗設置及網格劃分

對四柱結構的波浪繞射問題進行數值模擬。數值模型如圖1所示，以靜水面上各圓柱中心圍成正方形對角線交點為坐標原點建立直角坐標系，圓柱中心軸線分別位于(±1.45,0)和(0,±1.45)處，圓柱半徑為r=a，相鄰圓柱軸線間的距離為L=2.05 m，對角圓柱軸線間的距離為P=2.9 m，吃水深度T=0.5 m，水深d=3.65 m，規則波沿x軸正方向入射。

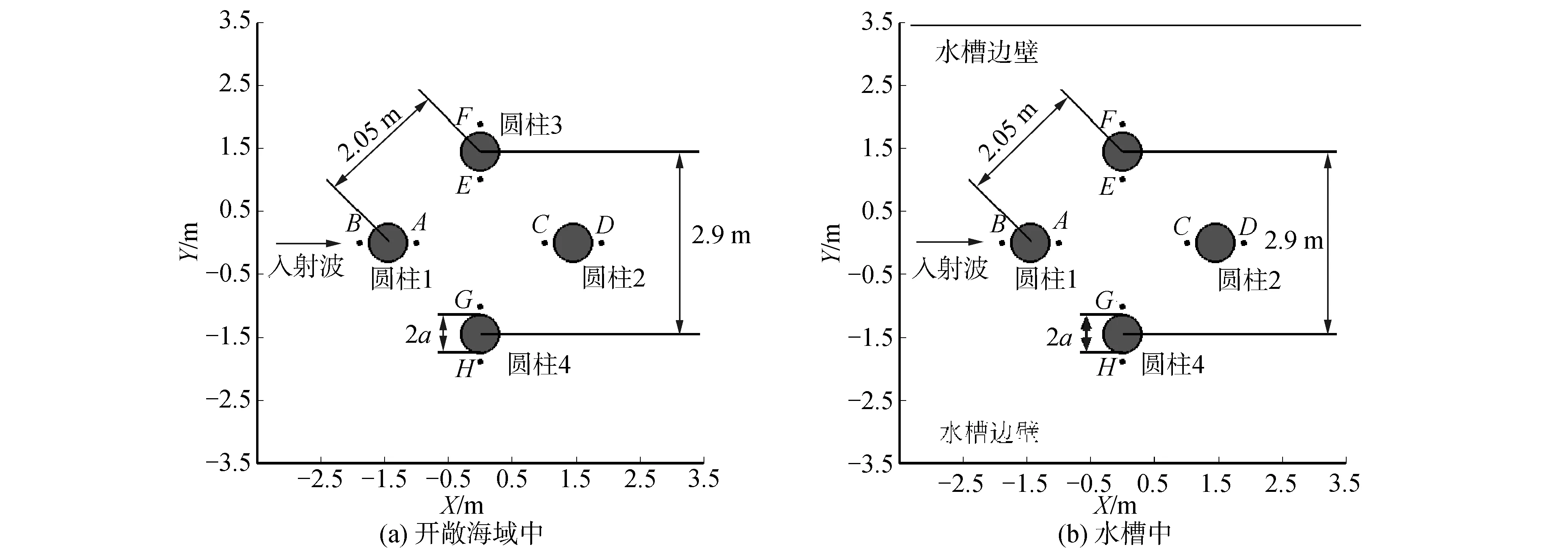
圖1 波浪作用下的四柱結構Fig.1 Four-cylinder structure in regular wave

為了保障數值計算精度，本文采用較密的網格剖分形式，如圖2所示。其中，每根圓柱面環向網格劃分64個，垂向和柱底徑向均劃分16個，四根圓柱表面共計劃分2 048×4個單元；在進行波面計算時，自由水面使用10 000個四邊形結構化網格。為了驗證所選網格的收斂性，分別采用前述的遠場方法和近場方法對a=0.30 m的四柱結構在x軸方向上的二階漂移力進行了計算，比較結果如圖3所示。從圖中可以看出，近場與遠場方法計算結果一致，說明本文網格可以獲得收斂結果。

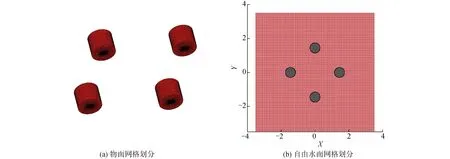
圖2 四柱結構的物面與自由水面網格劃分Fig.2 Sketch definition of four-cylinder structure and the mesh generation

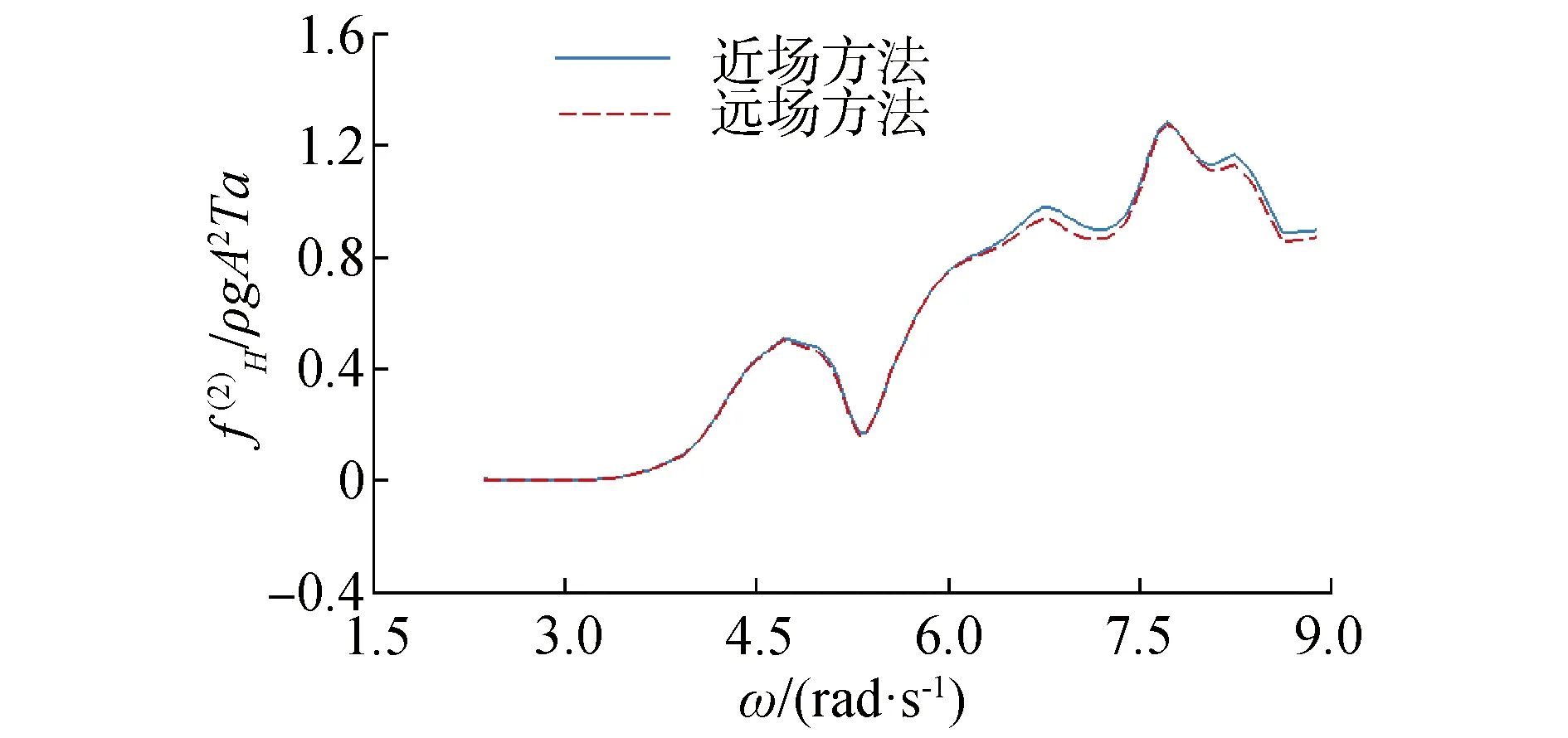
圖3 遠場方法和近場方法的二階漂移力比較Fig.3 Comparison of the second order drift force by far field and near field methods

將本文常數元方法無因次化計算結果與文獻[6]的高階邊界元方法對比，取r=a，L=4a布置下的四柱結構進行數值模擬，對圓柱內外2側測點處波高變化進行研究。從圖4中可以看出，本文計算結果與文獻[6]的數值結果符合較好，說明本文數值模擬的正確性。進一步對本文布置下各圓柱內外兩側關鍵點波浪爬行情況可以看出，當入射波頻率為ka=1.66 時，圓柱內側測點A出現明顯的波面升高，而外側測點B處波面顯著降低，說明波浪能量向圓柱內側集中，該現象稱為準陷波現象。通過上述對比可以看出，本文方法可以對該現象進行正確的模擬，可以應用于后文的數值分析。

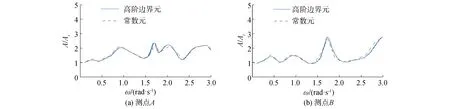
圖4 數值模型的驗證Fig.4 Verification of numerical models

3 開敞海域中圓柱半徑對結構附近波浪分布的影響

為考慮圓柱半徑對準陷波現象的影響，分別取a為0.30、0.35和0.40 m 3種情況進行研究。如圖1(a)與表1所示，在每根圓柱內外2側距離柱心1.1a處選取共8個測點記錄其位置的波高變化，計算結果如圖5所示。從圖中可以看出，當入射頻率ω為5.3、6.8、7.8 左右時各圓柱內側測點處的波高均出現明顯的峰值。對應地，外側測點在該頻率波高較低，波能由圓柱外側向內側集中，發生準陷波現象。上述3個頻率分別對應著一階、二階和三階準陷波模態。圓柱半徑的變化對圓柱內側測點的波高產生的影響明顯大于外側測點，隨著圓柱半徑的增大，圓柱內外2側波面高度分別增大和減小，意味著更多能量從圓柱外側向內側轉移，更多的能量被“俘獲”在四柱結構中。這是由于圓柱半徑的增加會導致圓柱側壁間距離的減小，導致結構內外水體接觸部分降低，增大了“俘獲”效果。

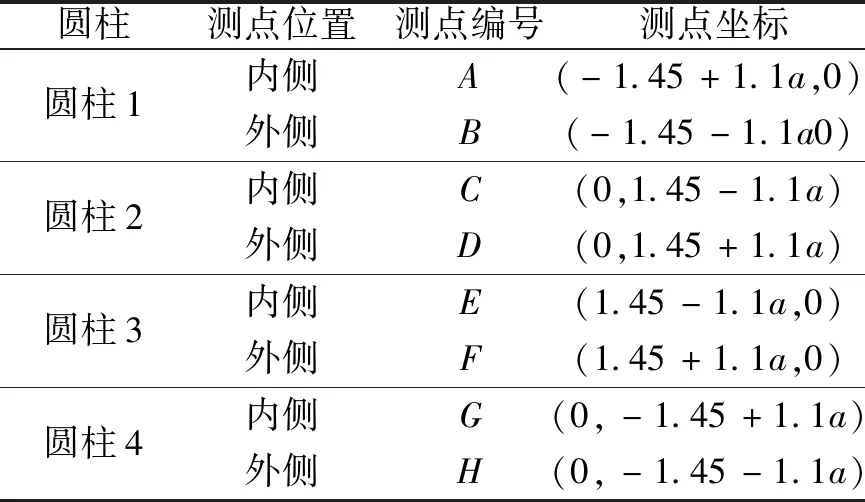
表1 四柱結構附近波高測點的坐標值Table 1 Coordinates of measuring points near the structure

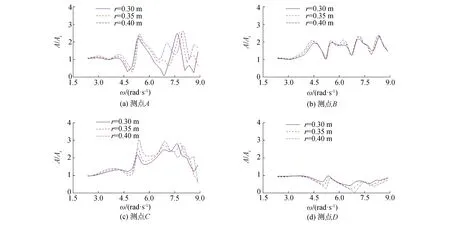
圖5 開敞海域中各測點處無因次波高隨頻率變化對比Fig.5 Variation of wave elevations at typical points under regular wave in open sea area

為了更好地觀察準陷波現象對整體波面的影響，給出3組工況下各階準陷波現象發生時結構附近無因次波高分布，如圖6所示。

從圖6中可以看出，各階準陷波模態的主要差異在于圓柱間波高的分布情況。一、二、三階準陷波模態分別對應相鄰圓柱間存在1、2、3個波，且最大波浪振幅總是出現在圓柱內側。結構后方出現明顯的低波高區域，進一步說明波能被四柱結構所“俘獲”，無法傳播到結構后方。相對而言，二階與三階準陷波模態后方波高明顯小于一階準陷波模態的情況，這主要是由于高階模態對應頻率較高，波長較小，因而結構物遮擋效應更為明顯。進一步對圖5與圖6中準陷波模態發生時圓柱內側波面隨圓柱半徑的變化進行研究，根據文獻[1-3]的理論解，準陷波模態對應波數為kL=nπ，(n=0,1,2,…)，即準陷波現象發生頻率只與圓柱間距有關。但是，根據本文數值結果，半徑的增大可以使準陷波模態的頻率向高頻移動，且對高階準陷波模態影響較為顯著，如表2所示。這主要是由于理論解基于無窮多個圓柱平行放置的假設，并且在推導過程中，將圓柱間距轉化為水槽寬度。實際上，圓柱半徑對準陷波模態的影響不可忽略，導致準陷波現象發生的關鍵因素實際為圓柱側壁間距。為驗證這一結論，表2給出了準陷波模態發生時圓柱側壁間距與波長的變化，可以看出，不同條件下kl可以更好地滿足nπ的關系，尤其是對于圓柱半徑較大的情況。進一步對比可以發現，三階準陷波模態所對應的自振頻率與kl=nπ的關系相比更遠，這主要是由于三階準陷波模態發生時，圓柱間形成的駐波并未在相鄰圓柱中心連線附近，而是偏向于結構的外側，如圖6(c)、(f)、(i)所示。上述對比說明了圓柱半徑對準陷波模態有顯著影響，不僅導致其自振頻率的變化，也會導致波面分布特征的改變。

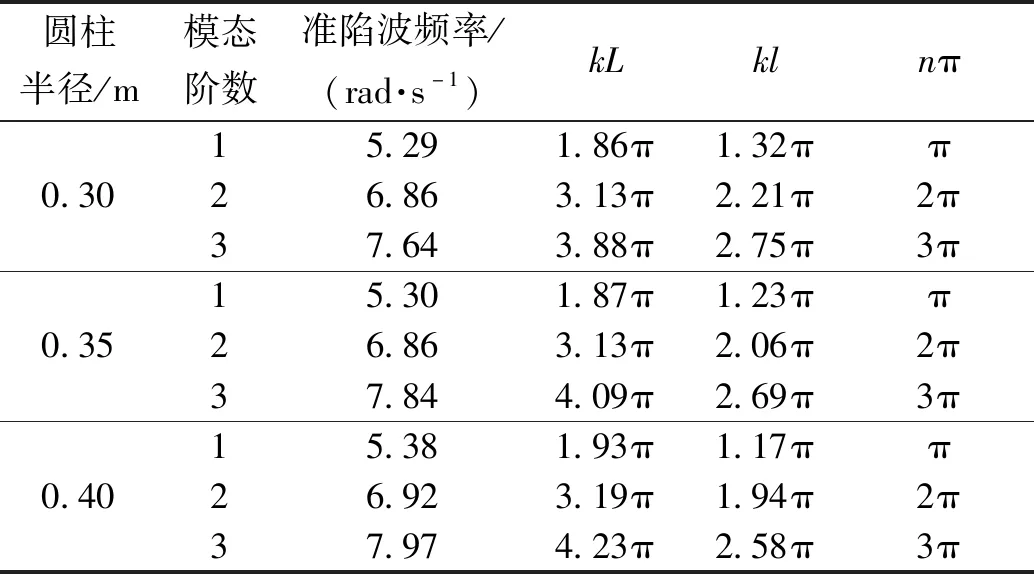
表2 四柱結構各階準陷波模態的發生頻率Table 2 Frequency of different order near-trapped modes of a four-cylinder structure

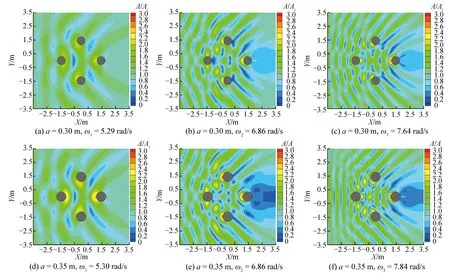
圖6 開敞海域中準陷波現象發生時四柱結構周圍波面分布Fig.6 Wave distribution around four-cylinder structure when near-trapping phenomenon occurs in open sea area

4 水槽邊壁效應對準陷波現象的影響

在上述分析的基礎上，對物理模型實驗中水槽邊壁對準陷波模態的影響進行研究，模型布置如圖1(b)所示。以開敞海域下半徑a=0.30 m的四柱結構為基礎，考慮該結構在W=7 m寬的水槽中心條件下各測點的波面變化情況。從圖7中可以看出，在考慮邊壁效應的影響后，各測點波面隨波浪頻率的變化曲線呈現更加劇烈的上下振蕩特征，原開敞海域準陷波現象發生頻率處的波高顯著增加，說明水槽邊壁效應對準陷波現象具有顯著影響。

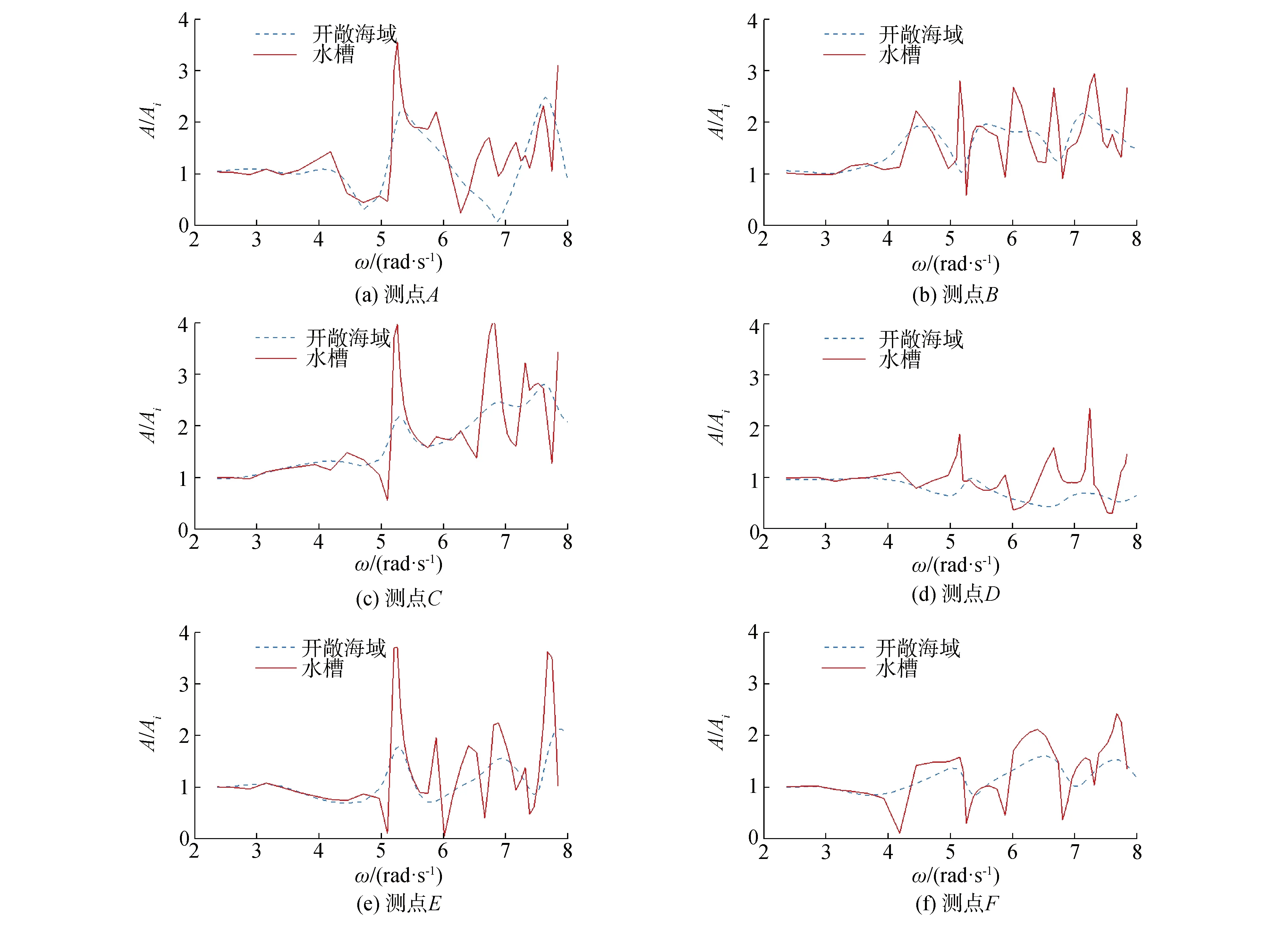
圖7 水槽側壁對四柱結構內外側測點波高變化的影響(r=0.30 m)Fig.7 Influence of sidewall on wave elevations at typical measuring points under regular wave (r=0.3 m)

為對比不同圓柱半徑條件下水槽邊壁效應的影響，圖8給出了3種半徑時后方圓柱內外兩側測點波高隨頻率的變化情況。水槽邊壁效應對不同半徑圓柱條件下準陷波模態的影響基本相似，各測點波面隨波浪頻率仍呈現劇烈震蕩特征，且峰值個數與發生頻率基本一致。為進一步探索上述現象的原因，水槽寬度為波長整數倍時對應頻率即為水槽橫向自振頻率[13]，表3通過對比發現橫向立波自振頻率與圖8中的波高變化峰值基本對應。進一步將結構準陷波模態頻率與水槽共振頻率進行對比，可以看出，水槽共振頻率與準陷波頻率存在耦合作用，一、二、三階準陷波頻率分別與水槽橫向立波自振頻率的二、四、五階模態接近，2種共振模態同時激發，導致對應頻率下波高峰值的顯著增加，說明水槽物理邊壁對準陷波現象具有顯著影響。

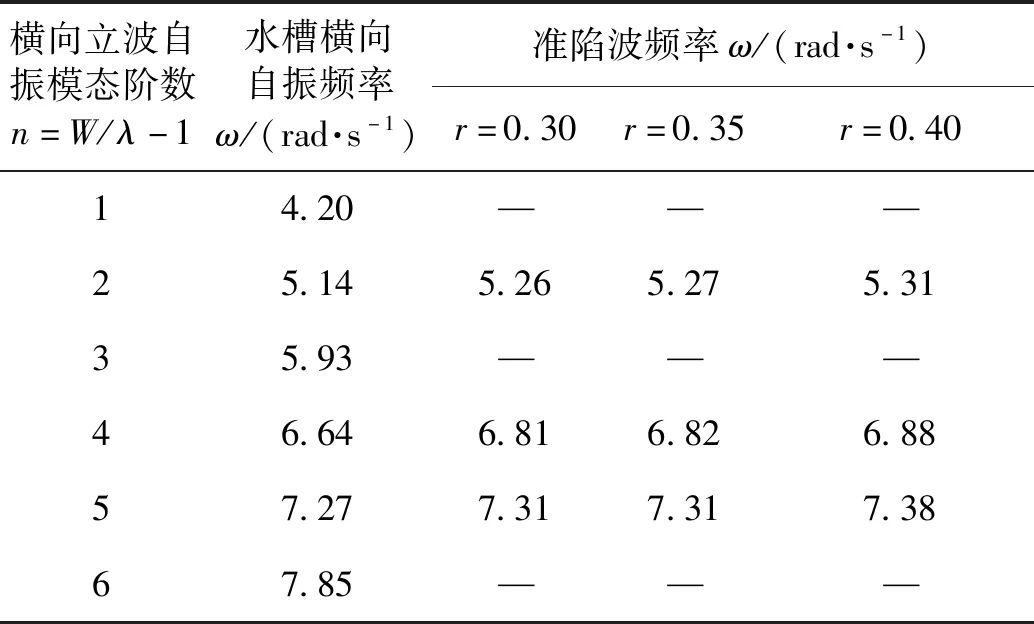
表3 水槽橫向共振頻率與準陷波頻率的對比Table 3 Frequency of horizontal resonance and near-trapping

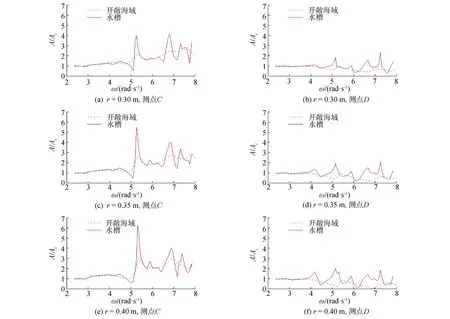
圖8 不同圓柱半徑時水槽側壁對后方圓柱內外兩側測點波高的影響Fig.8 The influence of the side wall of the flume on the wave elevation at typical measuring points of the rear cylinder

進一步對比發現，盡管圓柱半徑對準陷波模態頻率有一定影響，但總是對應于水槽橫向立波二、四、五階自振頻率，因而水槽邊壁效應對圓柱半徑的影響并不敏感。

為進一步考慮水槽側壁對準陷波模態的影響，圖9給出了水槽側壁影響下準陷波現象發生時結構周圍的波面分布情況。相比而言，圖6中圓柱附近波浪分布多數沿圓柱結構±60°方向呈現條狀分布，而圖9中圓柱附近波浪呈現出塊狀分布，尤其是對于二階與三階準陷波模態時短波的情況，這主要是由于波浪作用于圓柱后繞射波作用在水槽側壁后反射的結果。通過與圖6對比可以看出，結構附近大波高區域與小波高區域分布總體上更加清晰，說明邊壁效應影響下波能向圓柱內側集中的趨勢更加明顯。但是，圖6與圖9中所給出不同準陷波模態時最大波高分布基本相同。通過上述對比可以看出，與開敞海域相比，由于水槽中邊壁的反射作用導致水槽橫向立波自振模態的產生，更重要的是，波浪在作用于圓柱以后，由于繞射波受到水槽邊壁的反射作用，導致波浪波能無法輻射到遠場，而是集中于水槽內向下游傳播，導致圓柱附近波浪運動顯著增大，且波能向圓柱內側集中的趨勢更加明顯，這也導致了結構附近最大波高的增加。

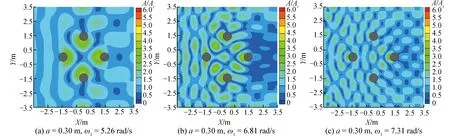
圖9 水槽中四柱結構周圍的波面分布Fig.9 Wave distribution around four-cylinder structure in channel

5 結論

1)圓柱半徑的變化對圓柱內側測點的波高產生的影響明顯大于外側測點，發生準陷波現象時此差異更為明顯。圓柱側壁間距的改變不僅導致準陷波模態自振頻率的變化，也會導致波面分布特征的改變。圓柱側壁間距離的減小導致結構內外水體接觸減少，更多的波能集中到結構內側。

2)與開敞海域相比，水槽中邊壁的反射作用會導致水槽橫向立波自振模態的產生。水槽邊壁的反射作用，導致波浪波能無法輻射到遠場，導致圓柱附近波浪運動顯著增大，且波能向圓柱內側集中的趨勢更加明顯，這也導致了結構附近最大波浪爬高的增加。

本文的研究工作忽略了圓柱壁附近的流體粘性阻尼和能量耗散對波面的影響，且實際情況下海洋平臺并非一直處于靜止狀態，所以需要借助Navier-Stokes方程數值求解實現更深入的工作，并對水流和波浪共同作用下的多樁柱式結構水動力特性進行拓展研究。雖然本文的研究工作尚有不足，但對開展水槽物理模型試驗和優化多樁柱式海洋平臺工程設計是具有意義的。