外部光注入的光泵浦自旋垂直腔表面發射激光器中的兩個混沌偏振分量對兩個復雜形狀目標中的多區域精確測距*

鐘東洲 曾能 楊華 徐喆

(五邑大學智能制造學部, 江門 529020)

基于外部光注入的光泵浦自旋垂直腔表面發射激光器(vertical cavity surface-emitting laser, VCSEL)的兩個混沌偏振分量, 提出了對兩個復雜形狀目標中的多區域精確測距方案.這里, 兩個混沌偏振探測波具有飛秒量級快速動態并且被雙極性sinc 波形調制, 使它們具有時空不相關特性.利用這些特性, 通過計算多束延時反饋混沌偏振探測波形和與之相對應的參考波形的相關性, 實現了對兩個復雜形狀目標多區域位置矢量精確測量.研究結果表明, 對多區域小目標的測距具有非常低的相對誤差(低于0.94%).當光電探測器的帶寬足夠大時, 其測距的分辨率達到0.4 mm, 并具有很強的抗噪聲能力.本文的研究結果在復雜形狀目標的精確測距方面具有潛在應用.

1 引 言

隨著人工智能的飛速發展, 激光雷達在自動駕駛、無人機、機器視覺和目標跟蹤測量等領域發揮著重要作用[1?5].通過感知周圍環境, 激光雷達有望實現以下功能: 目標精確測距、高質量三維(3D)成像、目標跟蹤和識別、自動定位和地圖繪制.目前, 大多數激光雷達測距方案[6?8]都使用脈沖激光器和連續波激光器作為光源, 以獲得更好的信噪比和測量范圍.然而, 基于脈沖激光器和連續波激光器的雷達測距具有分辨率低、攔截概率高、抗干擾能力弱、成本高等缺點.具有光反饋或光注入的半導體激光器產生的光混沌信號, 經天線發射后容易形成混沌激光雷達(chaotic lidar, CLR).與使用脈沖激光器和連續波激光器進行測距相比,CLR 對目標測距具有許多優勢[9?13], 例如攔截概率低、抗干擾能力強和成本低.此外, 由于受益于光學混沌的寬帶寬, 因而具有高分辨率.最后, 由于CLR 對激光參數的敏感性, 很容易生成和控制.

已報道的關于CLR 測距的工作主要關注的是通過發射的混沌信號(參考信號)和從目標反射回來的延遲信號的相關性來實現測距[14?20].在最近報道的工作中, 通過使用不同裝置, 基于互相關理論的CLR 測距取得了一些進展.例如, 2014 年,Zhang 等[18]實驗論證了一種基于微波光子混沌信號生成和光纖分布的超寬帶雷達遠程測距系統.2015 年, Wang 等[19]利用損耗介質研究了混沌雷達系統對目標檢測與測距的性能.同年, Yao 等[21]演示了一種基于波分復用技術的分布式多輸入多輸出混沌雷達.2017 年, 利用兩個混沌外腔半導體激光器的外差產生的寬帶白混沌雷達, Wang 等[16]理論探索了一個測距分辨率和抗干擾能力得到加強的雷達系統.2018 年, Cheng 等[22]利用自零差和時間門控技術產生一個脈沖外差混沌激光雷達,以提高混沌激光雷達能量利用效率, 結果實現了目標測距的精度達到毫米量級水平, 目標檢測范圍達到100 m 以上.最近, 利用驅動-響應垂直腔面發射激光器(vertical cavity surface-emitting laser,VCSEL)系統的同步混沌偏振探測信號, 我們實現了兩個目標的實時測距[23,24].此外, 利用三節點VCESLs 網絡中的6 個同步混沌偏振探測信號, 我們探索了6 個方位目標測距[25].

據我們所知, 相關CLR 測距的分辨率在很大程度上受到混沌激光器帶寬的限制.測距分辨率的進一步提高需要具有大調制帶寬的超快速混沌激光器.最近提出的光泵浦自旋VCSEL[26]具有吸引人的特性, 例如, 激光輸出的靈活自旋控制、飛秒量級的快速動態和大的調制帶寬.光注入或光反饋的光泵浦自旋VCSEL 發射的超快混沌探測信號有望用于提高目標測距的分辨率和精度.此外, 在己報道的關于CLR 測距的工作[14,19,22,27,28]中, CLR通常用于目標中的固定點.另外, 這些工作沒有使用多束CLR, 測距目標數量受限于少量目標.文獻[27?29]提出的相關CLR 測距的方案和方法不能完全檢測目標中不同區域的距離, 不適合復雜形狀目標中整個區域的精確測距, 基于相關CLR 的探測波形在目標測距前沒有被設計, 這影響了目標測距的分辨率和精度的進一步提高.為了克服這些問題, 復雜形狀目標中多區域CLR 測距的理論和物理機理需要進一步探索, 實現的新方案和方法也需要進一步探討.因此, 本文基于外部光注入的光泵浦自旋VCSEL, 通過利用雙極性sinc 波形調制的兩個混沌偏振波形, 提出了一種新穎的方案來實現兩個復雜形狀目標中的多區域精確測距.在這個方案中, 兩個調制的混沌偏振波形具有時間和空間上不相關的特性, 以及飛秒量級的快速動態特性.利用這些特性, 通過計算多束延時反饋混沌偏振探測波形和與之相對應的參考波形的相關性, 探討了兩個復雜形狀目標中的多區域測距的機理和實現方法.最后論述了兩個復雜形狀目標中多區域的測距分辨率和相對誤差.

2 理論和模型

圖1 給出了基于外部光注入的光泵浦自旋VCSEL 的兩個混沌偏振波形對兩個復雜形狀目標的多個區域進行精確測距的實現方案.其中, DFB(distributed feedback laser)是外部注入激光器.下標為1, 2 的光學隔離器(optical isolator, OI)用于確保光波的單向傳播.中密度濾波器(neutral density filter, NDF)用于控制來自DFB 的外部光場的注入強度.為了確保將DFB 的偏振光平行注入到光泵浦自旋VCSEL(spin-VCSEL)的x偏振分量和y偏振分量中, 來自DFB 輸出的偏振光需要通過偏振控制光路(polarization control optical circuit, PCOC)進行分離和調整為x偏振分量(xpolarization component,x-PC)和y偏振分量 (y-PC).PCOC 的偏振控制功能相關的描述詳見文獻[30].在PCOC中, 一些無源器件, 如光纖偏振器(fiber polarizer, FP)、光纖偏振控制器(fiber polarization controller, FPCO)、 光纖消偏器(fiber depolarizer, FD)、光纖偏振耦合器(fiber polarization coupler, FPC), 被用來實現x偏振分量和y偏振分量之間的轉換.目標1 (target 1,T1)和目標2 (target 2, T2)是被測量的復雜形狀目 標.PD (photodetector)是光電探測器.AM(amplitude modulator)是振幅調制器.EA (electric amplifier)是電放大器.TA (transmitting antenna)和RA(receiving antenna)分別是發射天線和接收天線.光注入光泵浦自旋VCSEL 產生的混沌光波通過光纖偏振分束器(fiber polarization beam splitter, FPBS)分為兩個偏振分量, 其中x偏振分量被1 × 1 光纖分束器1 (fiber beam splitter 1, FBS1)進一步分成兩束光波.其中一束光被考慮為參考信號, 另外一束光被用來作為探測信號, 為了便于討論, 它們分別被定義為x偏振參考信號和x偏振探測信號.同時, FBS2將y偏振分量進一步分離為兩束光, 其中一束光作為參考信號, 另一束光考慮為探測信號, 分別被命名為y偏振參考信號和y偏振探測信號.針對復雜形狀目標T1的測距,x偏振探測信號通過1 ×NFBS1分為N束探測波形.利用帶有下標為11—1N的振幅調制器, 這些探測波形被雙極性sinc 波形調制.這些調制后的探測波形被下標為11—1N的光電探測器PD 轉換為N條支路探測電流信號, 接著被下標為1—N的電放大器EA1放大.利用下標為11—1N的發射天線, 這些放大的電流信號被發射為N束雷達波, 之后到達目標T1的多個區域目標.當N束雷達波被目標T1中的多個目標小區域反射或散射之后, 首先被延時, 然后被接收天線RA1接收, 最后被電放大器EA2放大.另一方面,x偏振參考信號被1 ×NFBS2分成N束參考波形.利用下標依次為21—2N的振幅調制器, 這些參考波形被雙極性sinc 波形調制.這些調制后的參考波形被下標依次為21—2N的光電探測器PD 轉換為N條支路參考電流信號.探測電流信號與對應的參考電流信號之間的相關性可通過相關函數計算模塊(correlation function calculation module,CFCM)進行計算.通過觀察相關性最大期望值的時間位置, 使用目標測距計算模塊(target ranging calculation module, TRCM), 進一步計算目標T1中的多個區域目標的位置矢量.使用相同的方法,可以獲得目標T2中的多個區域的目標位置矢量.

圖1 基于外部光注入的光泵浦自旋VCSEL 的兩個混沌偏振波形對兩個復雜形狀目標中多個區域的精確測距方案.這里,DFB: 分布式反饋激光器; OI: 光學隔離器; NDF: 中密度濾器; PCOC: 偏振控制光路; FP: 光纖偏振器; FPCO: 光纖偏振控制器;FD: 光纖消偏器; FPC: 光纖偏振耦合器; PD: 光電探測器; AM: 振幅調制器; Spin-VCSEL: 自旋VCSEL; FPBS: 光纖偏振分束器;FBS: 光纖分束器; EA: 電放大器; TA: 發射天線; RA: 接收天線; T1 和T2: 兩個待測目標; CFCM: 相關函數計算模塊; TRCM: 目標測距計算模塊; x-PC: x 偏振分量; y-PC: y 偏振分量; η : 泵浦光的歸一化總泵浦功率Fig.1.Schematic diagram of the precise ranging for the multi regions of two complex-shape targets by using two chaotic polarization radars in the optically pumped spin-VCSEL with optical injection.Here, DFB, distributed feedback laser; OI, optical isolator;NDF, neutral density filter; PCOC, polarization control optical circuit; FP, fiber polarizer; FPCO, fiber polarization controller; FD,fiber depolarizer; FPC, fiber polarization coupler; PD, photodetector; AM, amplitude modulator; Spin-VCSEL, spin vertical cavity surface emitting laser; FPBS, fiber polarization beam splitter; FBS, fiber beam splitter; EA, electric amplifier; TA, transmitting antenna; RA, receiving antenna; T1 and T2, two targets to be measured; CFCM, correlation function calculation module; TRCM, target ranging calculation module; x-PC, x polarization component; y-PC, y polarization component; η , total normalized pump power.

針對自旋VCSEL, 光場的左旋和右旋圓偏振分量改寫為正交線性分量, 即

其中,E+和E–分別為是左右圓偏振分量的復振幅,Ex和Ey分別為兩個正交線性分量(x-PC 和y-PC)的復振幅.基于方程(1), 利用修正的自旋相關模型[31], 可以獲得外部光注入的光泵浦自旋VCSEL的四個耦合速率方程如下:

這里, 下標x和y分別表示x-PC 和y-PC; 圓偏振電場分量被晶體雙折射耦合, 其中, 用速率γp和二向色性γa來描述晶體雙折射的特征; 在方程(2)—(5)中, 歸一化的載流子變量M和n分別定義為M=(n++n?)/2和n=(n+?n?)/2 , 其 中n+和n?分別是相應的歸一化上旋和下旋電子密度;κ是腔衰減速率;α是線寬增強因子;γ是電子密度衰減速率;γs是自旋弛豫速率;η=η++η?是泵浦光的歸一化總泵浦功率, 其中,η=1 表示泵浦閾值.η+和η?是無量綱圓極化偏振泵浦分量, 用來描述極化偏振光光泵浦功率; 泵浦橢圓極化率P定義 為[32]P=(η+?η?)/(η++η?);kxinj和kyinj分別是x-PC 和y-PC 的注入強度;β是自發散射系數, 也稱為噪聲強度.ξ1和ξ2都是均值為0,方差為1 的獨立高斯白噪聲, 其中2δijδ(t ?t′).?ω是DFB 的中心頻率和Spin-VCSEL 的參考頻率之間的失諧.

3 結果和討論

如圖1 所示, 通過使用N束混沌偏振雷達探測波, 待測區域T1和T2中的任何一個小區域能同時被檢測.在小區域目標處反射或散射后, 具有不同延時的N束混沌偏振雷達探測波形同時被接收天線RA 接收.在這種情況下, 根據相關理論[33],為了容易地探測每個小區域的位置矢量, 混沌激光雷達需要滿足時間正交不相關和時間空間不相關.盡管N束x偏振和y偏振混沌激光雷達探測信號容易滿足時間正交性, 但很難實現空間正交性, 這是因為它們在空間上波形是相同的.為了滿足這些條件,N束探測信號需要具有高質量自相關函數進行調制, 例如, 在–1 和1 之間變化的雙極性sinc 波形.下面以Spin-VCSEL 輸出的x偏振探測信號對目標T1測距為例, 闡述其測距原理.當用雙極性sinc 波形對N束x偏振探測信號進行調制時, 可以獲得調制后波形為

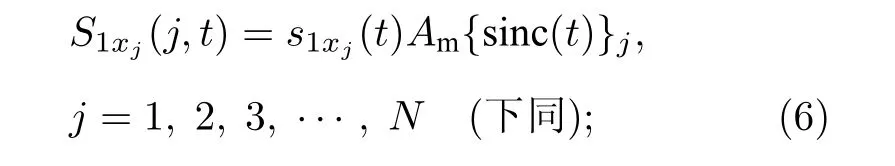
同理, 當用雙極性sinc 波形對N束x偏振參考信號進行調制時, 調制后的波形可以表達為

其中, Am為雙極性sinc 波形的幅值;{sinc(t)}j代表第j個sinc 波形, 當j取不同整數值時, 有不同的sinc 波形; 下標1 和2 分別表示探測信號和參考信號;s1xj,2xj=|E1xj,2xj|/max(|E1xj,2xj|) , 其中E1xj和E2xj分別為第j束x偏振探測信號和第j束x偏振參考信號的復振幅.根據方程(6)—(7),N束x偏振探測信號在空間上彼此正交, 其互相關可以表達為

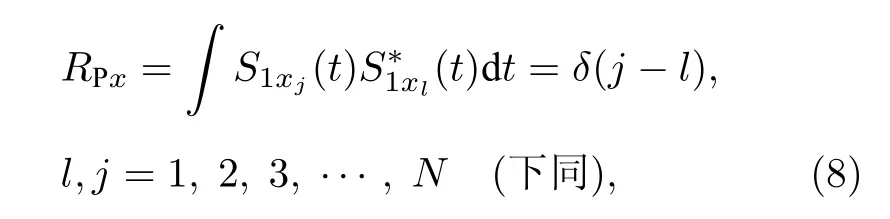
這里,S1xj和S1xl分別為第j束和第l束雷達探測信號.當j=l時,RPx= 1; 當j≠l時,RPx= 0,這意味著空間上不同束的雷達探測信號是互不相關的.此外, 對于同一束x偏振探測信號, 在不同時刻是不相關的, 但在同一時刻, 它是自相關的.因此, 對于第j束x偏振探測信號, 其時間自相關可以描述為

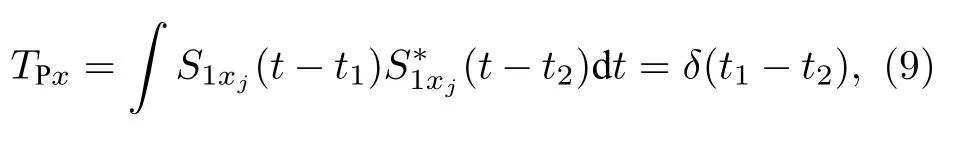
式中S1xj(t ?t1)和S1xj(t ?t2) 分別為第j束雷達探測信號在不同時間上的波形.當t1=t2時,TPx= 1;假如,TPx= 0.此外, 第j束x偏振雷達探測信號與第l束x偏振參考信號的空間互相關可以表達為

式 中S1xj(t ?t1)和S1xj(t ?t2) 分別為第j束雷達探測信號在不同時間上的波形.當t1=t2時,TPx= 1; 假如,TPx= 0.此外, 第j束x偏振雷達探測信號與第l束x偏振參考信號的空間互相關可以表達為

這里, 當t1=t2時,TPTx= 1;時,TPTx= 0.由方程(8)—(11), 可以得出第j束x偏振雷達探測信號與第l束x偏振雷達探測信號在時間和空間上的相關函數為

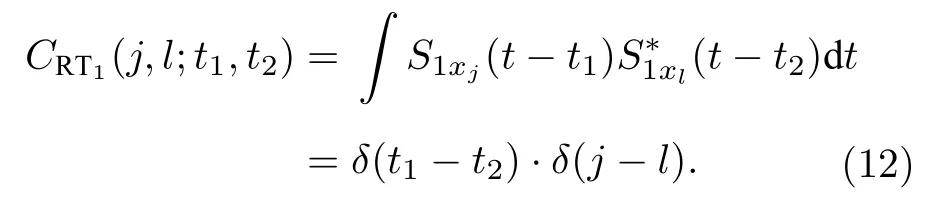
同時,N束x偏振雷達探測信號與第l束x偏振參考信號在時間和空間上的相關函數可以表示為

如圖2 所示, 分別考慮調制的N束x偏振雷達信號用于探測目標T1中的小區域中任意目標點A, 并通過其反射或者散射后, 被天線RA1接收.該天線接收信號可以表達為

其中,τ1,j是從發射天線TA1,j到接收天線RA1的時間延遲.因此, 根據方程(13)和方程(14), 可以得到來自RA1的接收信號和第j束x偏振參考信號的互相關函數為

式中Tint是有效的相關時間.時間延遲τ1j可以估計為最大相關性對應的時間值, 表示為

其中,ε是期望值.如圖2 所示, 將A點的實際位置矢量設為rA, 用第j束x偏振雷達探測信號對A點目標測量所得到位置矢量設定為rAj.第j個發射天線TA1,j的位置矢量設置為r1,j.接收天線RA1的位置矢量設為rr1.根據A點的幾何關系,可以得到

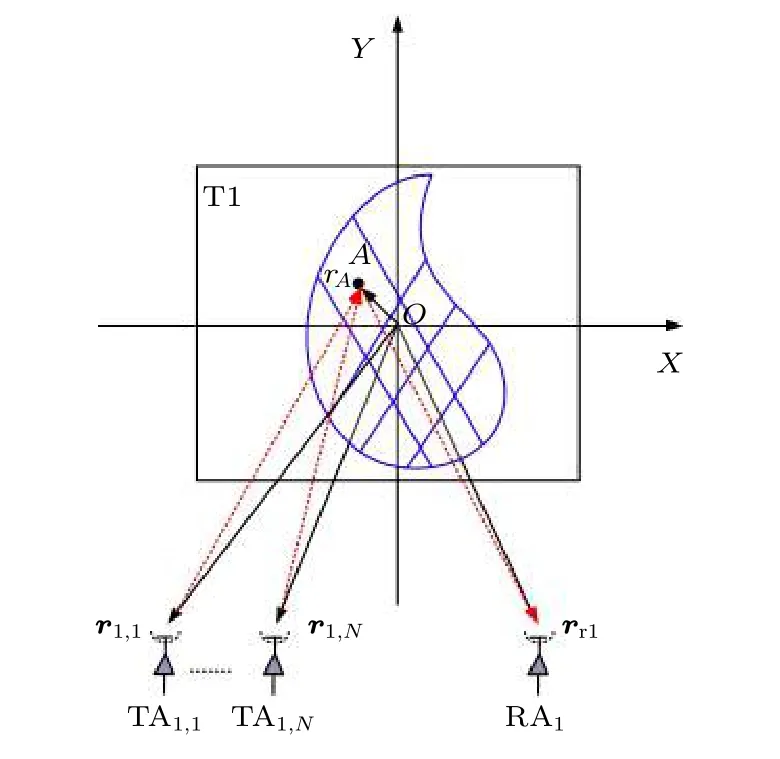
圖2 復雜形狀目標T1 中的任意小區域測距的幾何圖.圖 中, r A : A 點的實際位置矢量; r 1,1—r1,N : 發射天線TA1, 1—TA1, N 的位置矢量; r r1 : 接收天線的位置矢量; 紅色點線: 天線發射的雷達探測信號指向目標點A 的方向,以及由目標點A 反射或散射的雷達探測信號指向接收雷達RA1 的方向Fig.2.Geometry diagram of the ranging for arbitrary small area of the target T1.Here, r A , the actual position vector of the point-A; r 1,1–r1,N , the position vectors for the transmitting antennas TA1, 1–TA1, N ; Red dotted lines, the direction of the radar probe signals transmitted by the antennas toward the point-A, as well as the direction of the radar probe signals reflected or scattered by the point-A toward the receiving antenna RA1.

由方程(17), 可以通過求解個方程, 得到個A點的位置矢量.取這些位置矢量值的平均值作為A點的精確位置矢量, 表達式為

表1 列出了下面用于計算的系統參數值.這里使用四階Runge-Kutta 方法對方程(1)—(5)進行數值計算, 其中, 時間步長h為1 ps, 時間離散采樣點總數L= 100000.雙極性sinc 波形的抽樣周期Ts為0.1 ns, 對應的抽樣點數Ns為100.雙極性sinc 波形的抽樣周期數K0=L/Ns=1000.于是,第j個調制信號離散化的表達式為 s inc(t)j, 離散化的表達式為

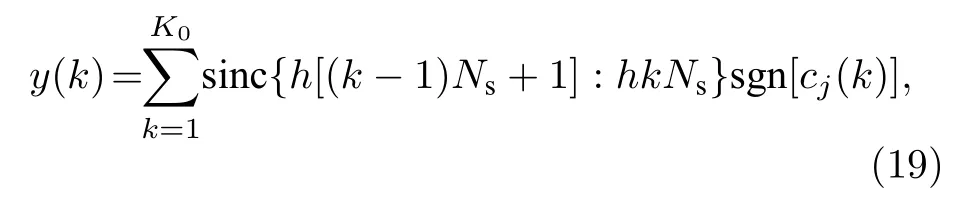
其中,

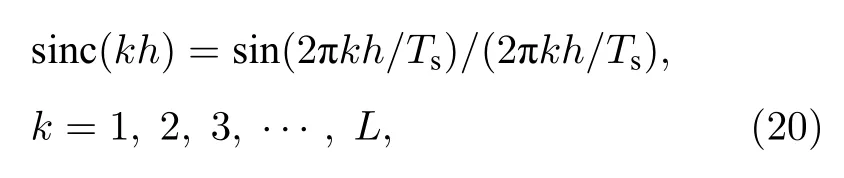
并且

這里,cj(k) 為數值0 和1 的隨機分布序列.當j取不同的整數值時,c(k) 有不同隨機分布序列, 從而獲得不同的sinc 波形.如圖3(a)和圖3(b)所示, 當j= 1 和3 時, s inc(t)1和 s inc(t)3的時間軌跡是不同的, 它們的值以不同的分布狀態介于–1 和1 之間.圖3(c)和圖3(d)給出了來自Spin-VCSEL輸出的第1 束和第3 束x偏振探測信號的時間軌跡.可以看出,x偏振探測信號時間軌跡呈混沌狀態.這兩束x偏振探測信號被雙極性sinc 波形調制后的時間軌跡(S1x1(t)和S1x3(t) )分別如圖3(e)和圖3(f)所示.從圖中可以發現, 它們的時間軌跡也呈混沌狀態和飛秒量級的快速動態特征.表明從天線發射的雷達探測信號的時間軌跡是混沌的, 具有快速動態特征, 以及滿足時間和空間上的不相關性(見方程(12)和方程(13)).為了方便討論, 讓N束x偏振雷達探測信號放置在一條水平線上.這里以第5束x偏振混沌激光探測信號為例, 計算它們的時間自相關(TPx)以及空間互相關(RPx), 計算結果如圖4 所示.可以看出,TPx的最大值出現在t= 0處.除t= 0 外,TPx在其他時間上的值幾乎都為0.RPx的峰值出現在j= 5 處, 在除5 之外的其他j值上都等于0.根據方程(12)和方程(13), 圖5(a)給出了10 束x偏振雷達探測信號的相關函數CRT1的時空演變.可以看出, 針對第N束x偏振雷達探測信號,CRT1的最大值發生在t= 0 和j=N處(N= 1, 2, 3, ···, 10, 以下相同).圖5(b)進一步給出了10 束x偏振雷達探測信號與10 束x偏振參考信號的相關函數CRT2的時空演變.從圖5(b)可以發現, 第N束x偏振雷達探測信號和第N束x偏振參考信號的相關性CRT2的最大值出現在t= 0 和j=N處.圖5 所示的結果表明, 在經過調制的N束x偏振雷達探測信號中, 兩兩之間具有時間和空間不相關的特性.同時, 經過調制的N束x偏振雷達探測信號與其相應的參考信號也具有時空不相關特性.下面, 利用它們的時空不相關性, 以復雜形狀目標T1中12 個小區域目標為例, 討論對它們的測距.

表1 用于計算的系統參數值Table 1.Parameter values of the system for calculations.

圖6 給出了復雜形狀目標T1中12 個小區域的測距幾何圖.為了方便討論, T1中12 個小區域被定義為A1—A12, 在每個小區域中, 測量3—4 個目標點.如圖6 所示,= 1, 2, 3 或1, 2, 3, 4)的位置矢量被依次設定為發射天線(TA1,1—TA1,10)被排列成一條直線, 位置矢量依次設定為r1,1—r1,10, 具體如表2 所列.另外, 兩相鄰的發射天線之間的距離為0.5 m.這些發射天線發射的10 束x偏振雷達探測信號依次用于探測目標的距離.為了驗證對這些目標測距的可行性, 目標的實際位置矢量分別假定為具體表達式如表3 所列.為了進一步描述這些目標點的準確度, 引進相對誤差(relative error, RE)如下:

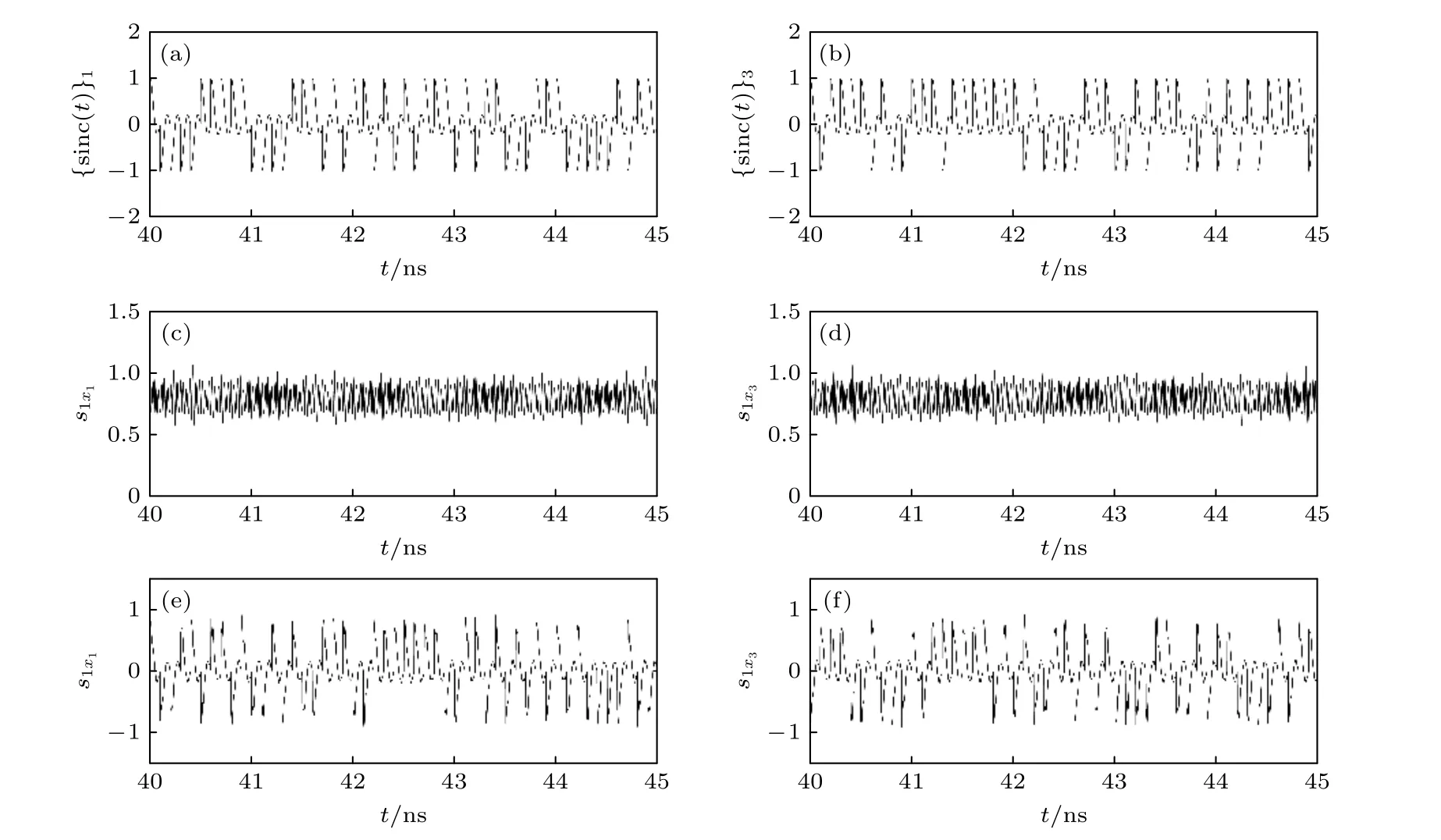
圖3 (a)用于調制第1 束x 偏振探測信號的sinc 波形的時間軌跡; (b)用于調制第3 束x 偏振探測信號的sinc 波形的時間軌跡;(c)第1 束x 偏探測信號( s 1x1 )的時間軌跡; (d)第3 束x 偏振探測信號( s 1x3 )的時間軌跡; (e)調制后的第1 束x 偏振雷達探測信號的時間軌跡; (f)調制后的第3 束x 偏振雷達探測信號的時間軌跡Fig.3.(a) Temporal traces of the sinc waveform which are used to modulate the first beam of the x-polarization probe signal; (b)temporal traces of the sinc waveform which are used to the third beam of the x-polarization probe signal; (c) temporal traces of the first beam of the x-polarization probe signal ( s 1x1 ); (d) temporal traces of the third beam of the x-polarization probe signal( s 1x3 ); (e) temporal traces of the modulated first beam of the x-polarization probe signal; (f) temporal traces of the modulated third beam of the x-polarization probe signal.

圖4 (a)第5 束x 偏振雷達探測信號的時間自相關( T Px ); (b)第5 束x 偏振雷達探測信號和數量為10 束的x 偏振雷達探測信號的空間互相關( R Px ), 變量j 表示第j 束x 偏振雷達探測信號Fig.4.(a) Time autocorrelation ( T Px ) of the fifth beam of the x-polarization radar probe signal; (b) space autocorrelation ( R Px )between the fifth beam of the x-polarization radar probe signal and ten beams of ones.Variable j denotes the j th x-polarization radar probe signal.

其中,j= 1, 2, 3, ···, 12.

表2 發射天線(TA1,1—TA1,10)的位置矢量Table 2.Position vectors of the transmitting antennas (TA1,1—TA1,10).

圖5 (a)在10 束x 偏振雷達探測信號中, 兩兩之間的時空相關性( C RT1 ); (b)10 束x 偏振雷達探測信號與10 束x 偏振參考信號的時空相關性( C RT2 ); 這里, 變量j 表示第j 束x 偏振雷達探測信號或第j 束x 偏振雷達參考信號Fig.5.(a) Time-space correlation C RT1 among ten beams of the x-polarization radar probe signals; (b) Time-space correlation CRT2of ten beams of the x-polarization radar probe signals with ten beams of the x-polarization radar reference signal.Here, the variable j denotes the jth x-polarization radar probe signal or the jth x-polarization radar reference signal.

圖6 復雜形狀目標T1 中12 個小區域目標測距的幾何圖.A1—A12: 12 個小區域目標; TA1,1—TA1,10: 10 個發射天線; r 1,1—r1,10 : 發射天線(TA1,1—TA1,10)的位置矢量;RA1: 接收天線; S 1x1—S1x10 : 10 束x 偏振雷達 探 測信號;Rx: 接收的雷達探測信號Fig.6.Geometry diagram of the ranging for twelve small areas in the complex-shape target T1.A1—A12, twelve small area targets; TA1,1—TA1,10, ten transmitting antennas;r1,1—r1,10, position vectors for the transmitting antennas(TA1,1—TA1,10); RA1, receiving antenna; S 1x1—S1x10 , ten beams of the x-polarization radar probe signals; Rx, received radar probe signals.

根據方程(16)給出的相關函數CC1的最大期望值, 可以得到一組延遲 時 間(τ1,1—τ1,10).在 此基礎上, 使用方程(17)和方程(18), 可以獲得目標T1中任意1 個目標點的測量位置矢量的平均值.下面以目標點為例, 討論其測距過程.當來自天線RA1接收的雷達探測信號(包括來自TA1,1—TA1,10發射天線的10 束x偏振雷達探測信號)用于探測目標時, 計算來自天線RA1接收的雷達探測信號與10 束x偏振參考信號的時空互相關(CC1,1—CC1,10), 結果如圖7(b)所示.可以看出,互相關的最大期望值依次位于10 個不同的延遲時間處.觀察圖7(c)可以得到10 個延遲時間如下:τ1= 34.149 ns;τ2= 32.770 ns;τ3= 31.443 ns;τ4= 30.182 ns;τ5= 29.004 ns;τ6= 27.932 ns;τ7= 26.994 ns;τ8= 26.222 ns;τ9= 25.652 ns;τ10= 25.316 ns.基于這10 個時間延遲, 使用方程(17)和方程(18), 計算得到測量的目標點的平均位置矢量為用同樣的方法, 可以得到目標T1中其他目標點測量的平均位置矢量, 結果列于表3 中.因此, 根據方程(22), 可獲得目標T1中目標點的測距相對誤差, 結果如表3所列.從表3可以看出,目標點的測距相對誤差在0%和0.94%之間.這些結果表明, 針對復雜形狀目標的多區域的測距, 本文所提供的方案具有較小的相對誤差(小于0.94%).

根據文獻[34], 相關峰的半極大處全寬(full width at half maximum, FWHM)通常用于描述測距分辨率(ranging resolution, RR).從圖7(d)可以看出, 相關函數CC1,1的FWHM 為8/3 ps.根據RR = (c× FWHM)/2, 得到RR 為0.4 mm,其中,c為真空中的光速.從圖7(c)可以觀察到:

CC1,1—CC1,10的FWHM 均為8/3 ps.這表明10束x偏振雷達探測信號對目標點的測距分辨率均能達到0.4 mm.用同樣的計算方法, 可以得到目標T1中的其他目標點的測距分辨率均為0.4 mm.為了觀察一些關鍵參數(如注入強度、自發輻射噪聲強度、目標點與雷達探測信號源的距離、光電探測器的帶寬、sinc 波形的振幅)對測距分辨率的影響, 下面以目標為例來闡述它們的依賴關系.圖8 給出了上述參數對目標點的測距分辨率的依賴關系.這里, 參數 d1是第1 束x 偏振雷達探測信號源與目標點之間的距離.由于這些雷達探測信號源被排列在水平線上, 且相互之間的距離不發生改變,因此, 當 d1在一定范圍內變化時, 其他的x 偏振雷達探測信號源與目標點之間的距離也發生相應的變化, 但它們之間的距離不發生變化.?f1是光電探測器PD11和PD21的帶寬.從圖8 可以看出,目標點的測距分辨率獨立于注入強度、自發輻射噪聲強度、目標點與探測信號的距離、sinc 波形的振幅.當這些參數在一定范圍內變化時, 它們的范圍分辨率始終保持0.4 mm.其他目標點的測距分辨率同樣與這些參數無關, 且都為0.4 mm.然而, 目標點的測距分辨率嚴重依賴于光電探測器(PD11和PD21)的帶寬.如圖8(c)所示, 當帶寬 ?f1從10 GHz增大到100 GHz 時, 測距分辨率從11.8 mm 快速地減小到1 mm.當帶寬 ?f1進一步從100 GHz 增大到250 GHz 時, 測距分辨率從1 mm 慢慢地減小到0.4 mm.當帶寬 ?f1在250—300 GHz之間變化時, 分辨率保持在0.4 mm.當其他光電探測器的帶寬發生改變時, 與其相應的其他目標點的測距分辨率有相同的變化.這些結果表明, 當光電探測器的帶寬足夠大時, 利用由雙極性sinc 波形調制的x偏振雷達探測信號對復雜形狀目標的多區域測距分辨率可達到0.4 mm.它們具有出色的強抗噪聲性能和穩定性.另外計算了第一束x偏振雷達探測信號與目標T1中的任意目標點之間的距離d對測距相對誤差的影響, 結果如圖9 所示.可以看出,當d在5.56—5.95 m 之間變化時, 目標T1中任意目標點的測距相對誤差RE 在0—0.94%之間變化.這說明x偏振雷達探測信號源與目標點的距離對測距相對誤差有很小的影響.

表3 目標T1 的每個小區域中3—4 個目標點的實際位置矢量和測量的位置矢量 及它們的相對誤差Table 3.Actual position vectorsof 3–4 target points in each small area of target T1 and the measured position vectors as well as their relative errors.

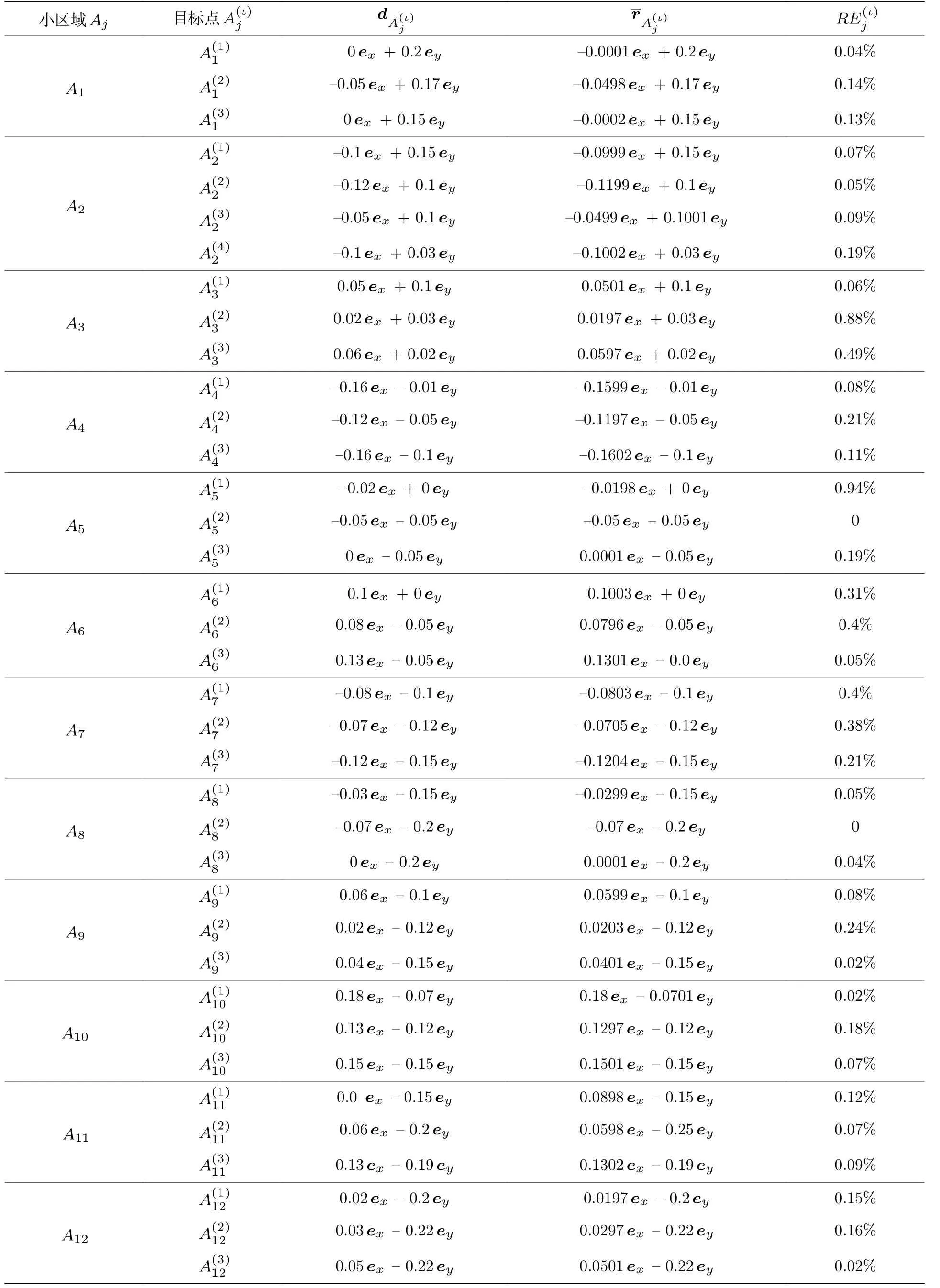
表3 目標T1 的每個小區域中3—4 個目標點的實際位置矢量和測量的位置矢量 及它們的相對誤差Table 3.Actual position vectorsof 3–4 target points in each small area of target T1 and the measured position vectors as well as their relative errors.

圖7 (a)針對目標點 從天線RA1 接收的雷達探測信號與10 束x 偏振參考信號的時間互相關; (b)針對目標 , 從接收天線RA1 接收的雷達探測信號與10 束x 偏振參考信號的時空互相關; (c)圖(a)的局部放大圖; (d)針對目標點, 從天線RA1 接收的雷達探測信號與第1 束x 偏振參考信號的互相關Fig.7.(a) For the target point- the time autocorrelations of the radar probe signals received by the antenna RA1 with ten beams of the x-polarization radar probe signals; (b) for the target point- the space autocorrelations of the radar probe signals received by the antenna RA1 with ten beams of the x-polarization radar probe signals; (c) local enlarged plot of panel (a); (d) for the target point- the time autocorrelation of the radar probe signals received by the antenna RA1 with the first beam of the xpolarization radar probe signal.

圖8 目標點的測距分辨率(RR)對一些關鍵系統參數的依賴關系 (a) RR 與注入強度 k xinj 的依賴關系; (b) RR 與第一束x 偏振雷達探測信號和目標點 之間的距離 d1 的依賴關系; (c) RR 與光電探測器(PD11 和PD21)帶寬 Δ f1 的依賴關系;(d) RR 與sinc 波形的振幅 A m 的依賴關系; (e) RR 與自發輻射噪聲強度 β 的依賴關系.此外, k xinj = k yinj , 除上述討論參數之外的其他參數值見表1Fig.8.Dependences of the range resolutions (RR) for the target point- on some key system parameters: (a) Dependence of the RR on the injection strength k xinj ; (b) dependence of the RR on the distance between the first beam of the x-polarization radar probe signal and the target point- ; (c) dependence of the RR on the bandwidths Δ f1 of the photo detectors (PD11 and PD21);(d) dependence of the RR on the amplitude of sinc waveform; (e) dependence of the RR on the spontaneous emission noise inten-sity β.Moreover, k xinj = k yinj , values of other parameters are shown in Tab.1.

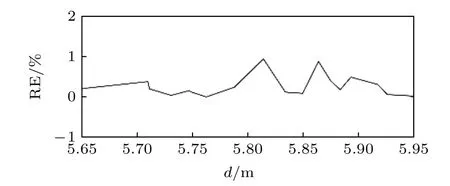
圖9 測距相對誤差RE 與目標T1 中任意目標點與第1 束x 偏振雷達探測信號源之間的距離d 的依賴關系Fig.9.Dependence of the ranging relative error RE on the distance d between the arbitrary target point and the first beam of the x-polarization radar probe signal source.

需要特別注意的是, 由于x偏振和y偏振雷達探測信號對目標T1和T2分別獨立測量, 并且測距原理相同, 因此, 在本文提出的方案中,y偏振雷達探測信號對目標T2的測距結果(包括測距分辨率和測距相對誤差)與x偏振雷達探測信號對目標T1的測距結果是幾乎相同的.另外, 本文提出的測距方案能夠實現0.4 mm 分辨率的關鍵現實條件是: 1)需要具有飛秒量級快速動態的激光光源; 2)需要用高質量自相關函數對激光器輸出的探測光波進行調制, 使其具有時空不相關特性;3)方案中涉及的相關光路中的光器件帶寬要足夠寬, 例如, 光電探測器的帶寬約100 GHz.

4 結 論

總之, 利用外部光注入的光泵浦自旋VCSEL產生的兩個混沌偏振分量, 提出了對兩個復雜形狀目標中多區域精確測距的新穎方案.在此方案中,兩個混沌偏振雷達探測信號被雙極性sinc 波形調制.調制混沌偏振雷達探測信號具有時空不相關和飛秒量級的快速動態的獨有特性.利用這些特性,通過觀察混沌偏振探測信號及相應的參考信號之間互相關的最大期望值對應的時間位置, 獲得來自多區域目標的延遲時間.基于這些延遲時間, 復雜形狀目標中多區域的位置矢量可以被精確測量.研究結果表明, 多區域目標的測距相對誤差很低, 小于0.94%.當光電探測器帶寬足夠大時, 它們的測距分辨率非常穩定, 可以達到0.4 mm, 并且具有很強的抗噪聲能力.本文提出的多區域目標測距方案具有如下吸引人的優勢: 具有穩定且高的測距分辨率、很強的抗噪聲能力、非常低的相對誤差.這些特性能夠迎合復雜形狀目標中多區域位置矢量測量的需要.