基于KPCA和優化ELM的齒輪箱故障診斷*

李夢瑤，周 強，于忠清

(青島大學數據科學與軟件工程學院，山東 青島 266071)

0 引言

齒輪箱是旋轉機械的一種關鍵傳動部件。工作環境往往十分惡劣而且復雜，若發生故障，不但會造成設備失靈，還會帶來安全隱患與難以估量的經濟損失[1]。因此，實時有效的齒輪箱故障診斷方法對降低設備維修成本，保障安全具有重要的意義。

齒輪箱的故障診斷關鍵在于信號故障特征提取和故障模式的分類識別。齒輪箱在傳動過程中，多個部件相互嚙合產生的振動會對故障部件的信號造成干擾，因此從多故障模式振動信號中提取有效的故障特征信息，仍是齒輪箱故障診斷中亟待解決的問題[2]。齒輪箱發生故障時振動信號通常表現為非線性，因此模式識別中使用較廣的是BP神經網絡和ELM等機器學習方法。程鵬等[3]將自組織映射與BP神經網絡相結合，提取齒輪箱的不同故障特征進行訓練，改進了BP的網絡性能。桂斌斌等[4]采用PSO-BP混合算法模型，對BP神經網絡進行優化，并將其應用于齒輪箱故障診斷，故障分類準確率有所提升。程加堂等[5]以風力發電機組齒輪箱為研究對象，使用小波分析降噪，建立混沌量子粒子群優化BP神經網絡診斷模型，提取典型故障特征進行故障診斷。雖然前期工作取得了一定效果，BP神經網絡仍存在多方面的局限性。ELM是一種單層前饋神經網絡，無需反復對隱藏層參數進行調整，相比傳統的分類方法，具有泛化性能好、計算復雜度低等優點。

然而，ELM的一個不足之處是穩定性差，原因在于其隱藏層的權值和偏置完全是隨機生成的，影響一定程度的分類效果。部分學者采用遺傳算法(Genetic Algorithm, GA)[6]、粒子群優化算法(Particle Swarm Optimization, PSO)[7]等優化ELM，改善網絡穩定性，但上述優化方法存在易于陷入局部最優、收斂速度慢等問題。蟻群算法作為一種啟發式優化算法，具有魯棒性、分布性，利于全局尋優等優點[8]，因此，論文選擇蟻群算法對ELM進行優化。針對復雜且非線性的齒輪箱故障信號，文中利用KPCA方法對特征矩陣進行降維與冗余剔除，將蟻群算法與ELM的優點相結合，提出基于KPCA特征提取與蟻群優化ELM的齒輪箱故障診斷方法，實驗表明，該方法的分類準確率較高，具有較優的故障診斷能力。

1 KPCA原理

核主成分分析是利用核函數將輸入空間映射到高維特征空間，在高維空間進行線性計算，提取非線性特征的方法[9]。設原始數據為x1,x2,...,xM，則協方差矩陣可以表示為：

(1)

其中，Φ為原始數據空間到特征空間F的非線性映射。求解矩陣CF的特征值與特征向量v，即：

CFv=λv

(2)

其中，特征值λ≥0，特征向量v∈F≠{0}。則有：

Φ(xv)CFv=λ(Φ(xv)v)

(3)

特征向量可由如下線性表示為：

(4)

則有：

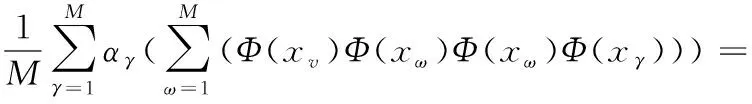
(5)

定義M×M維矩陣K，令Kij=[Φ(xi)Φ(xj)]。則式(2)可以化簡為：

Mλα=Kα

(6)

K的特征值λ1≥λ2…≥λM，其中特征值λi的累計貢獻率ηi計算公式為：

(7)

設定E值，計算各主分量的累計貢獻率。選取大于E值的前幾個主分量，構成新的樣本矩陣，將其作為診斷模型的輸入值。

2 ACA-ELM模型

2.1 ELM算法

ELM是一種新型的單隱含層前饋神經網絡[11]。其網絡結構如圖1所示。

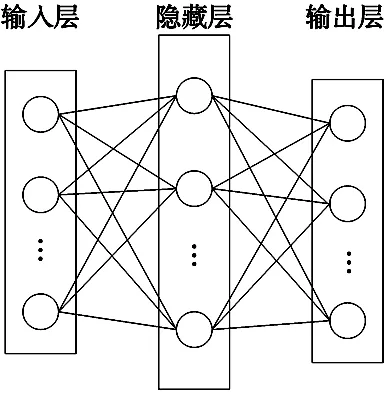
圖1 ELM網絡結構示意圖

對于N個不同的隨機樣本(xi,ti),i=1,2,...,N，其中，xi=[xi1,xi2,...,xin]∈Rn,ti=[ti1,ti2,...,tim]∈Rm。設隱藏層神經元數目為L，則網絡的輸出T為：

(8)

其中，g(·)為激活函數，a為輸入權值矩陣，b為偏置。

式(8)可簡化為：

Hβ=TT

(9)

其中，H為神經網絡的隱藏層的輸出向量。輸出權值矩陣β可由下式求得：

(10)

式中，H+是H的廣義逆矩陣。因為ELM的初始權重矩陣參數(ai,bi),i=1,2,...,N是隨機設置的，且在訓練過程中保持不變，可能使得部分參數數值為0，導致部分隱藏節點失效。除此之外計算過程的隨機性會影響神經網絡的預測結果，因此文中利用蟻群算法改進ELM中隨機產生的輸入層權值與偏置，提高預測精度。

2.2 蟻群算法優化ELM

2.2.1 蟻群算法

蟻群算法是學者在螞蟻覓食過程中受到啟示得到的一種仿生算法[12]。螞蟻在尋找食物時釋放一種信息素，濃度越高，選擇某路徑的概率越大。這種正反饋機制，加快了系統尋找最優解的速度，獲得全局的相對最優解[13]。蟻群通過信息素這一媒介，自組織過程形成高度有序的覓食行為，而不易陷入局部最優。

2.2.2 ACA-ELM模型

文中提出的ACA-ELM的模型，運用蟻群算法對ELM的輸入層權值與偏置進行優化，將最優的參數應用于齒輪箱故障診斷。蟻群算法在運用之前，將分量的參數進行W等分，即將輸入層權值與偏置的值按照其取值范圍平均劃分成W個子區間，將每個子區間的邊界值作為其對應的值，形成W級決策問題。初始時刻所有權值與偏置每個子區間的信息素量相同，隨機產生初次個體種群，得到每只螞蟻相應的路徑輸出，計算網絡輸出值誤差，重復上述操作；迭代過程中不斷調整信息素，搜索新信息素條件下的最優解，直到循環結束條件滿足時停止[14]。

文中蟻群改進ELM算法的流程如圖2所示。算法的基本步驟如圖2所示。

圖2 蟻群改進ELM算法流程圖

(1)初始化參數。初始化ELM網絡結構以及待優化參數的定義域，初始化蟻群算法螞蟻數目h、信息素初始值τ0、揮發系數ρ、信息素增強系數Q等；

(2)將待優化的參數數目確定為m，這些參數設為pi(1≤i≤m)，每個參數均包括W個值，其值等于W個子區間的對應值，形成集合Spi；

(3)啟動螞蟻。h只螞蟻從蟻穴出發，依次走過m個集合Spi，利用輪賭算法從集合Spi的W個元素中選擇出元素j，將其加入禁忌表Tabu，直至所有的集合完成元素的選擇；

(4)每只螞蟻走過的路徑構成了一組網絡參數，計算ELM網絡輸出值誤差，并記錄當前迭代的最優解與最優誤差ebest；

(5)全部螞蟻完成一次迭代后，對信息素進行更新，更新規則如式(13)所示：

τj(Spi)(t+1)=
(1-ρ)τj(Spi)(t)+ρΔτj(Spi)

(11)

(12)

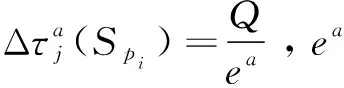
(6)重復步驟(3)～步驟(5)，直到迭代次數達到NCmax；

(7)求解全局的最優解，作為ELM的輸入層權值與偏置，輸入訓練樣本搭建ELM模型進行訓練，得到神經網絡預測結果。

3 實驗與分析

3.1 故障診斷流程

對齒輪箱的振動信號進行時域與頻域的故障特征提取，利用KPCA對特征向量進行降維，簡化網絡結構，將選取的特征向量輸入到ACA-ELM中進行訓練和測試，具體流程圖如圖3所示。

圖3 故障診斷流程圖

3.2 實驗數據與特征提取

實驗數據取自江蘇千鵬診斷故障診斷試驗平臺公開數據集。實驗采樣頻率為5.12 kHz，轉速為880 r/min，數據包括齒輪箱在6種工況下的振動數據，其運行狀態與理想輸出如表1所示。每種工況的齒輪箱振動數據截取120組樣本，每個樣本包含1024個數據點，其中每種工況選取100組用于訓練，20組用于測試。

表1 故障診斷系統理想輸出

圖4為對振動信號提取的時域與頻域的19個特征。不同的特征能夠反映不同方面的故障特性，但是維數越高，模型結構越復雜，影響分類效率。對于19維輸入數據，可能含有噪聲信息和冗余信息，為了有效提取主要的特征指標，提高分類效率與精確度，文中引入了KPCA方法，對輸入的特征指標進行降維。由于訓練數據的非線性特征，核函數選取高斯核函數。

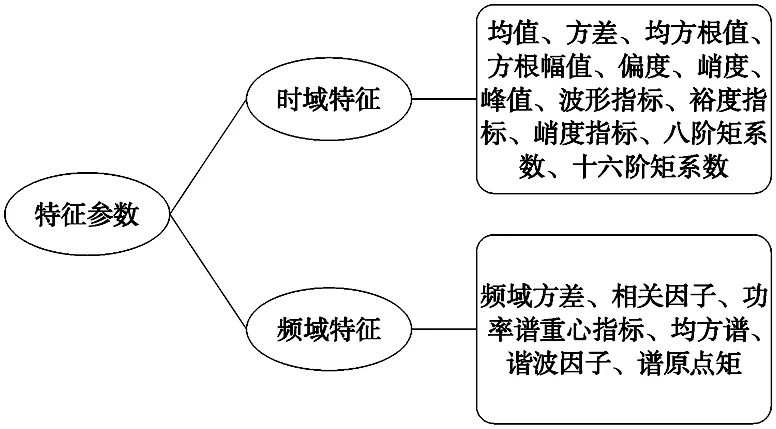
圖4 特征參數

表2為經過KPCA降維后的結果。由表2可知，前8個主成分的累計貢獻率為85.75%，超過了85%的理論要求[15]。即特征矩陣由19維壓縮到8維后，仍可以保留85.75%的特征信息，因此選取這8維特征代替原來的19維特征作為神經網絡的輸入，進行故障的識別與分類。

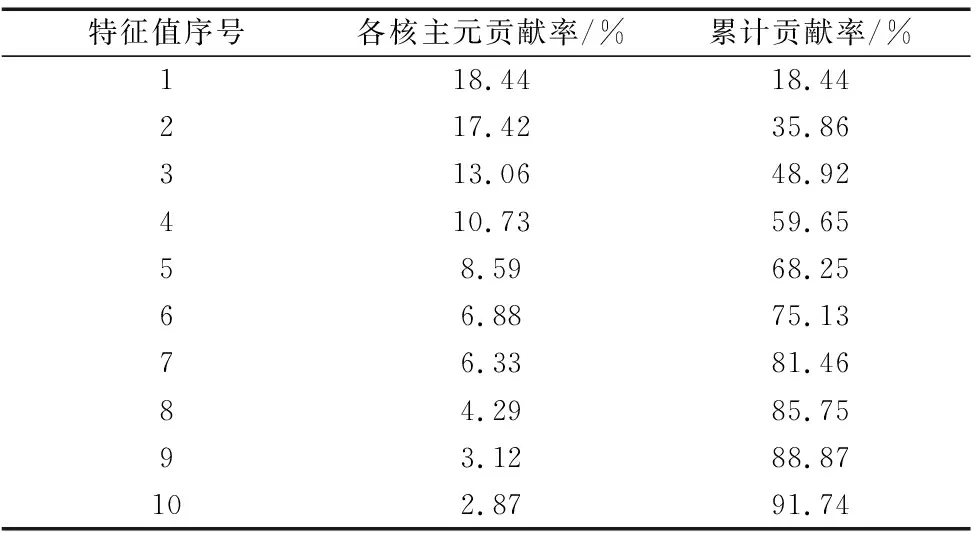
表2 各成分貢獻率

3.3 ACA-ELM模型在齒輪箱故障診斷中的應用

考慮訓練樣本中輸入向量的維度與故障類型的數目，確定最終的網絡拓撲結構為8-10-6。其中，8個經過KPCA提取的特征作為神經網絡的輸入，6種工況模式為神經網絡輸出，ELM隱藏層神經元個數設置為10，激活函數選擇Sigmoid。蟻群算法中：設置最大迭代次數NCmax= 200，h= 100，τ0= 1，ρ= 0.8，Q= 2。

基于以上參數，首先對提取的特征使用了KPCA方法進行降維，然后分別將降維前與降維后的特征作為ELM的輸入向量進行故障診斷。其分類準確率對比如表3所示。

表3 使用KPCA前后的準確率對比

從分類準確率對比值可以看出，使用KPCA 方法降維后，齒輪箱的特征矩陣維度大大降低，而故障分類準確率提高到了92%。這是因為原始特征矩陣為19維，其中包含了部分噪聲和冗余信息，降維操作可將部分無用信息剔除，使得降維后ELM分類精度從89%提高到了92%。

針對降維后的數據樣本，分別應用ELM與ACA-ELM模型進行實驗，從圖5、圖6可以看出，ELM的分類準確率為92.5%，ACA-ELM的分類準確率為98.33%。通過對比可以知道，運用蟻群算法對ELM的權值和偏置進行優化，對于點磨與磨損故障的診斷更加準確，有效的提高了ELM的預測精度。

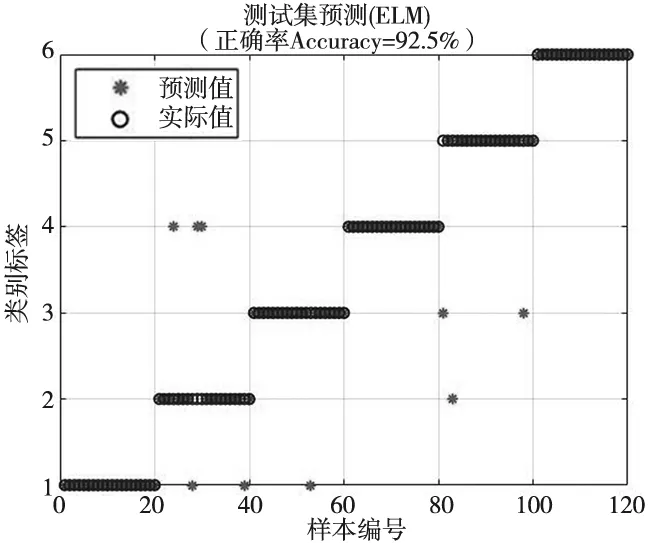
圖5 ELM分類結果

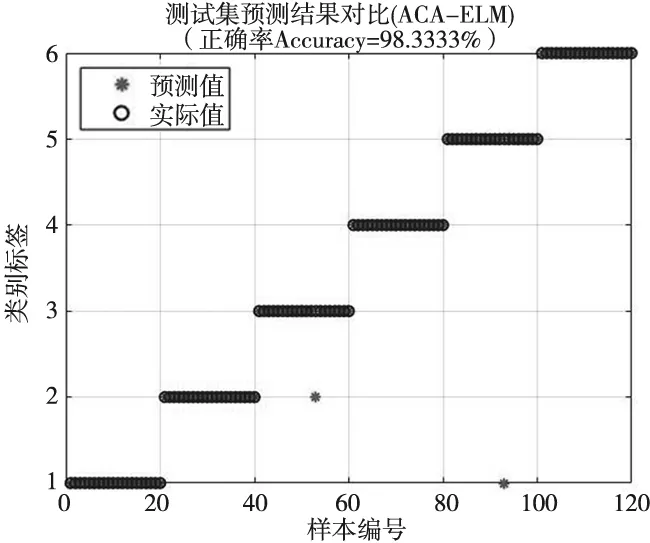
圖6 ACA-ELM分類結果

為了驗證文中所提方法的有效性與泛化性，分別與ELM、BP、ACA-BP、GA-ELM模型進行比較，為了避免計算時的偶然性，5種方法均計算10次取平均值，其性能對比結果如表4所示，診斷精度對比如圖7所示。

表4 不同模型的故障診斷結果對比

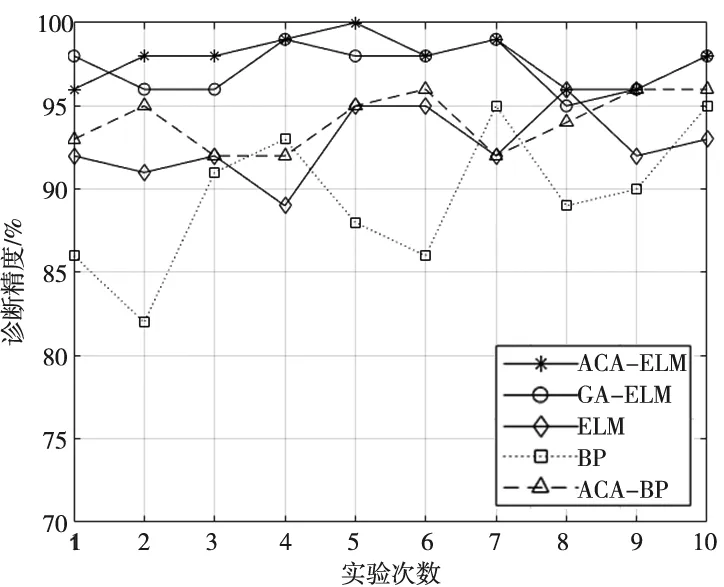
圖7 不同模型的診斷精度對比圖

由表4和圖7可知，從診斷精度來說，BP模型的泛化性能不佳，誤差較大，與ELM模型相比，BP的平均均方根誤差高出0.462 7。ACA-BP模型對BP模型進行了優化，精度有所改善,表明蟻群算法對神經網絡的優化是有效果的。ACA-ELM模型優化了ELM，提高了診斷精度，平均均方根誤差降低0.726，優于GA-ELM算法。從模型訓練時間來說，ACA-ELM模型的運行速度優于其余對比模型。從圖7可以看出，ACA-ELM模型數據預測的波動幅度小，趨于平穩，具有更好的診斷精度，表明蟻群算法有效的改善了ELM的穩定性與分類效果。因此文中所提方法能夠有效的識別齒輪箱的故障類別并達到實時性要求，能夠應用于齒輪箱的故障診斷。

4 總結

文中利用蟻群算法全局優化算法的優勢，提出了基于KPCA與優化極限學習機(ACA-ELM)的算法模型，將其應用于齒輪箱故障診斷中，得到結論如下：

(1)采用KPCA方法對高維特征數據進行降維，提取有效的特征指標，減少了冗余信息，使得網絡結構大大簡化，提高了模型的分類效率與準確率。

(2)針對ELM固有的隨機性，將蟻群算法與ELM進行耦合，優化ELM 神經網絡的輸入層權值和偏置。將ACA-ELM模型應用到齒輪箱的故障診斷中，顯著地提高了診斷的準確度，與其他算法相比，可以在短時間內達到較高的診斷精度，綜合性能更佳，為齒輪箱的故障診斷方法提供了新的思路。