基于載荷譜的轉向架焊接構架疲勞可靠性分析*

辛俊勝，商躍進，薛 海，楊朋朋，張潔娟

(蘭州交通大學機電工程學院，蘭州 730070)

0 引言

轉向架是鐵路機車車輛的重要組成部分，而焊接構架又是軌道車輛轉向架的主要零部件之一，起著承載、連接以及傳遞載荷的作用[1]。軌道車輛的車輪在運行一段時間后會因滾動接觸、牽引、制動和車輛振動等多種因素的影響而產生磨耗，使得輪軌間作用力增大，從而導致焊接構架在服役過程中應力隨之增大，容易產生疲勞裂紋，影響車輛的運行安全。

在轉向架疲勞壽命研究當中，相關學者做了諸多研究：盧耀輝等[2]參照UIC 515-4標準對比分析了考慮焊縫和不考慮焊縫的客車構架疲勞強度，并繪制構架Goodman曲線；劉旭等[3]選取構架箱體梁為研究對象，以靜強度為基礎建立了主焊縫關于名義應力、結構應力和缺口應力的三種應力模型，并進行壽命預測；文獻[4-5]根據焊接結構疲勞失效的特點發展了熱點應力和缺口應力的分析方法，排除了接頭名義應力的分散性。焊接件的焊縫是最容易出現疲勞破壞的部位，而且疲勞破壞通常發生在焊縫的焊趾處，并沿著焊趾在厚度方向上擴展[6]；文孝霞等[7]對焊接構架焊縫參數進行敏感性分析，表明焊接厚度和焊接熔深將直接影響焊縫的壽命；王紅等[8]選用熱點應力法對焊接構架疲勞壽命進行了預測，由于熱點應力法考慮了應力峰值的影響，因此相對于名義應力法精度有所提高。

考慮隨機變量的不確定性對焊接構架壽命的影響，文章以應力強度理論為基礎，建立可靠性狀態函數，并采用一次二階矩法對焊接構架薄弱焊縫處進行可靠性分析，以概率的形式描述構架運行安全性，并對隨機變量進行靈敏度分析。該方法可為轉向架焊接構架的設計、結構改進及制定維護策略提供參考。

1 可靠性設計理論

1.1 可靠性分析

可靠性分析是通過由狀態函數的概率分布求出的可靠性概率，其結果是由影響狀態函數的隨機變量所決定的[9]。狀態函數由式(1)表示：

Z=R-S=g(X)，X=[x1,x2,···,xn]

(1)

式中,R為結構強度；S為工作應力；X為隨機變量參數，n為影響可靠度參數的數量。

一次二階矩法是求解可靠度常用的解析方法，通過將非線性的狀態函數展開成線性狀態函數，從而計算出可靠性指標并求出可靠度。

(2)

則狀態函數的均值和標準差為：

μZ=g(μX)

(3)

(4)

狀態函數g(X)對各隨機變量X求偏導為：

(5)

則可靠性指標和可靠度分別為：

(6)

(7)

1.2 可靠性靈敏度分析

可靠性靈敏度反應了各隨機變量參數對機械可靠度影響的大小，靈敏度絕對值越大，說明該參數對可靠性影響越明顯。根據可靠度計算公式推導出各隨機變量均值和方差的靈敏度計算公式分別為式(8)、式(9)：

(8)

(9)

其中,

(10)

(11)

(12)

2 構架靜強度分析

2.1 有限元模型建立

高速動車組轉向架焊接構架主要由管狀橫梁、縱向連接梁和側梁焊接為H型，為了提高計算效率，依據焊接構架結構特點及受載情況，對不影響求解結果的一些孔以及圓角結構等進行簡化處理。根據構架整體尺寸，并考慮焊縫處應力仿真結果的準確性，在Hypermesh軟件中，采用C3D8R單元進行有限元網格劃分，共生成 918 501個單元，432 098個節點。圖1為轉向架有限元模型。

圖1 焊接構架有限元模型

2.2 載荷工況及邊界條件

參考UIC 615-4與EN 13749標準，考慮了電機載荷、焊接吊座載荷等外載荷，組合共得到直線驅動、直線制動、曲線驅動、曲線制動等49種運營工況[10]，在這里只列出載荷條件復雜的第49載荷工況下所對應的應力云圖，如圖2所示。

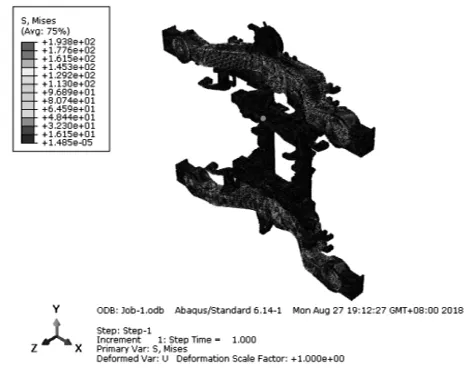
圖2 第49種工況下應力云圖

構架局部應力分析如表1所示[11]，由表1可知轉臂定位座立板與側梁下蓋板焊縫連接處的應力幅值最大，因此選取此處來代替整個構架進行可靠性分析。

表1 構架局部應力分析

3 載荷譜

3.1 車輛動力學模型建立

根據350 km/h公里級車輛表2的相關參數建立的高速動車組多體動力學模型如圖3所示。

隨著互聯網電子商務的不斷發展，自助售賣機和各種自助服務已基本成熟，提供了適宜電商與自助家庭化的物質保障，在大中型城市已經廣泛應用。

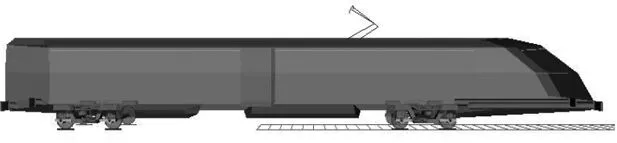
圖3 車輛多體動力學模型

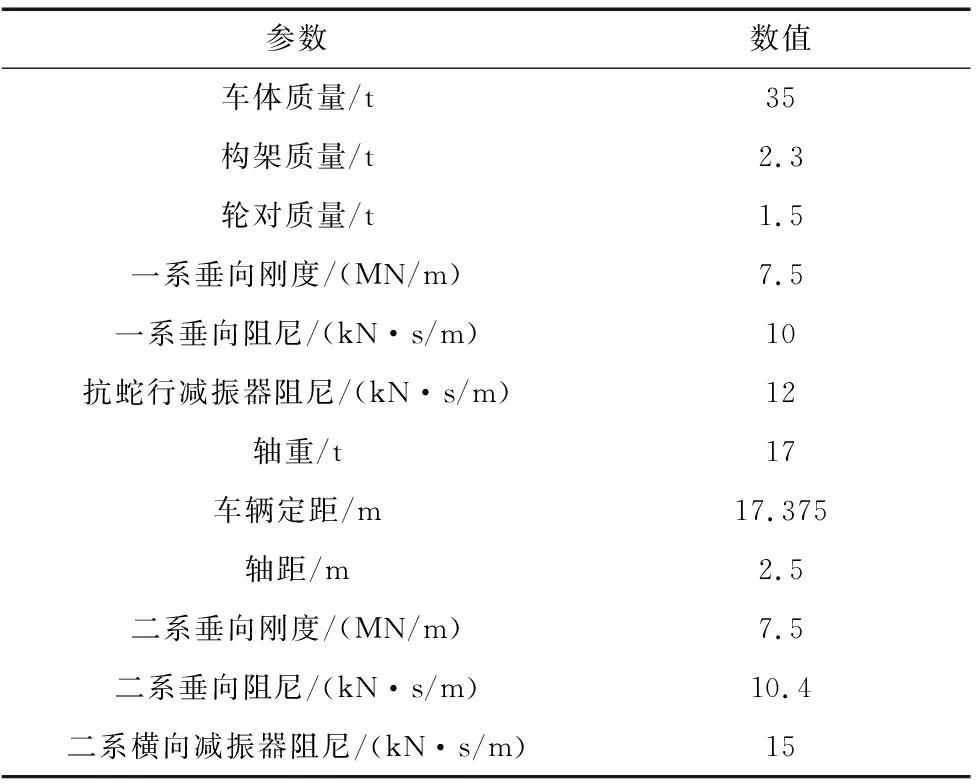
表2 車輛主要參數

3.2 分級載荷譜

選取直線運行以及曲線通過兩種工況類型，直線工況下設置列車行駛速度為350 km/h，曲線通過工況下設置列車行駛速度為300 km/h；列車行駛時間均設置為50 s。高速動車組動力學模型轉臂處的采樣頻率為200 Hz，載荷數據采集時間為50 s，因此共得到1.0E4個載荷信號并，對轉臂定位座焊縫區域進行分級統計。

由于采集到的載荷數據樣本量較大，采用8級譜分級數所反應的載荷數據不完整，因此，選擇載荷譜分級數為16級，以5%的載荷幅值作為門檻值[12]，對轉臂定位座焊縫區域在直線運行條件以及曲線運行條件時的載荷頻次分別進行分級統計，得到兩種運行條件下的16級載荷譜如表3所示。

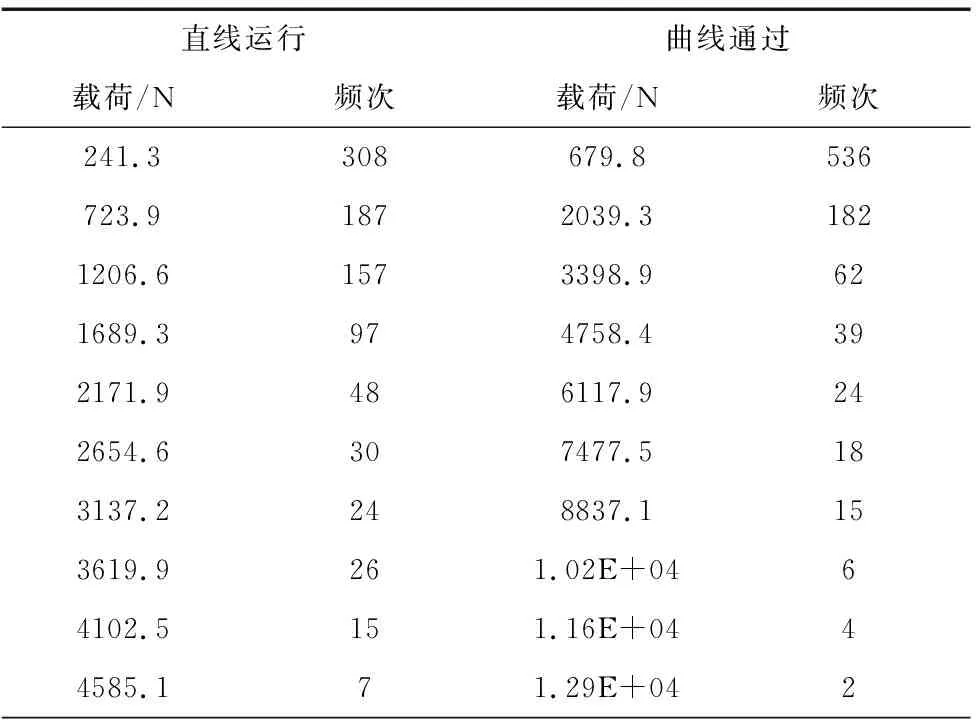
表3 轉臂定位座位置載荷譜

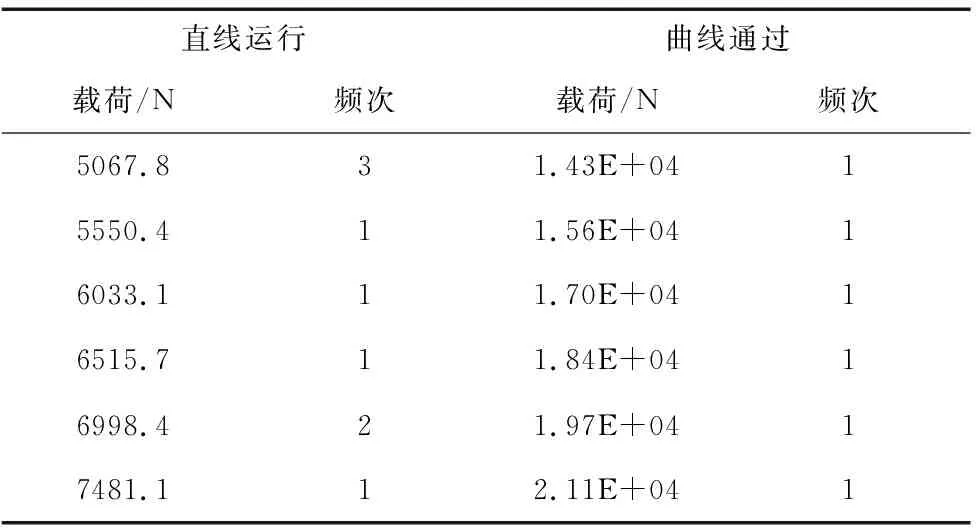
續表

3.3 載荷與應力轉化關系

對構架進行可靠性分析需要得到相應的應力譜，因此要將載荷譜轉化為應力譜。轉向架構架動應力與動載荷之間具有線性對應關系，因此可根據有限元的計算結果與所加的載荷值求解出與之對應的比例系數，具體結果按照式(13)進行求解：

(13)

式中：σeqc代表相應的Von-mises應力；F代表標準規定的相關載荷。為了得到更加精確的焊縫區域的應力值，本文采用子模型法對轉臂定位座進行分析。根據圣維南定理，必須滿足切割邊界遠離模型要研究的應力集中的區域[13]，對轉臂定位座與箱型梁下蓋板處建立詳細的角接焊縫結構并進行精細網格劃分。圖4所示為所建子模型有限元模型(包含4條角接焊縫)。判斷子模型建立正確性的方法是對比切割邊界區域的應力應變結果與全局模型是否一致，如果結果一致，則認為該子模型是有效的。通過驗證得出該有限元模型的邊界滿足子模型要求，如圖5所示。

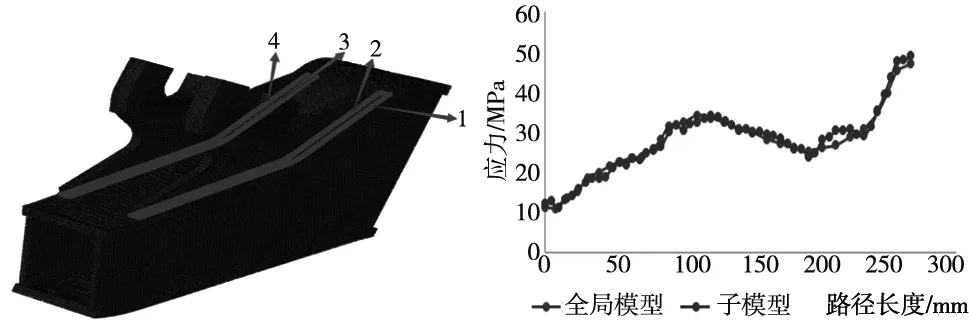
圖4 子模型有限元模型 圖5 子模型邊界驗證

所提取子模型轉臂定位座與箱型梁下蓋板連接焊縫的應力值，由于最大應力節點出現在第二條焊縫所在位置，因此在這里只列出第二條焊縫所有節點隨焊縫長度變化的應力值如圖6所示，選取最大應力值所對應的節點進行載荷轉換系數K的計算。根據公式(1)計算得到載荷-應力轉換系數為K=1.71。

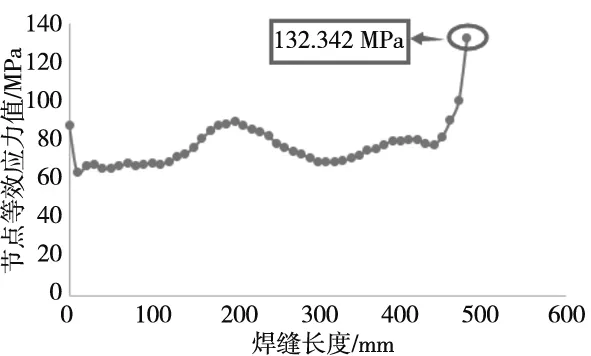
圖6 第二條焊縫節點應力值

4 可靠性靈敏度分析

轉臂定位座焊縫處等效應力計算公式為：

(14)

式中，L為車輛運營公里數；L1為實測公里數；N為循環次數，取200萬次；m為材料常數，取m=3.5；K為轉換系數；Fi為第i級載荷譜幅值；ni為第i級載荷幅值對應的循環次數[11]。

則可靠性狀態函數為：

(15)

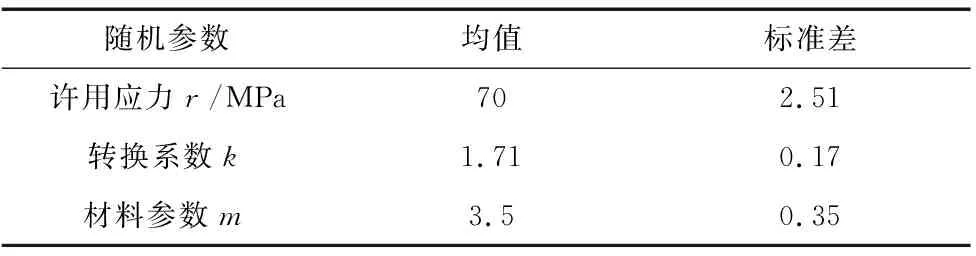
表4 參數表

通過一次二階矩法計算焊接構架可靠度隨運行里程的變化曲線如圖7所示，并通過Monte-Carlo法進行驗證。由圖7可以看出：

(1)車輛運行至1000萬公里以后，焊接構架可靠性開始降低，當運行至1200萬公里時可靠度為0.998 7，滿足3σ設計要求；

(2)兩種方法計算得到的可靠度結果非常接近，故采用一次二階矩計算可靠度結果可以接受。

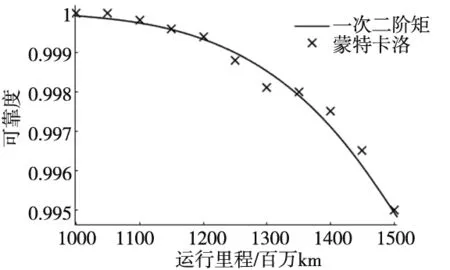
圖7 可靠度變化曲線

圖8、圖9分別為各隨機參數均值和方差隨運行里程對可性度的靈敏度曲線，由圖8和圖9可以看出：

(1)各參數均值對可靠度的影響中，轉換系數k對可靠性影響最為明顯，許用應力r影響最小；

(2)各參數方差對可靠度的靈敏度均為負值，且載荷-應力轉換系數k靈敏度絕對值最大。

圖8 參數均值靈敏度

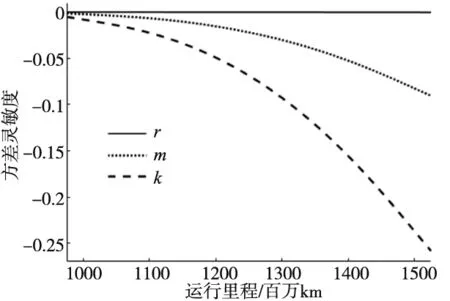
圖9 參數方差靈敏度

5 結論

(1)對轉向架焊接構架進行有限元分析，得到轉臂定位座焊縫處應力幅值最大，進而對應力薄弱區采用子模型法進行分析計算，得到了更加精確的焊縫區應力值，并求得載荷-應力轉換系數K=1.71。

(2)以強度-應力干涉理論為基礎，建立可靠性狀態函數，并采用一次二階矩法對轉臂定位座焊縫處進行可靠度計算和靈敏度分析，并采用Monte-Carlo法驗證了一次二階矩計算可靠度的準確性。

(3)車輛運行至1200萬公里時，焊接構架可靠度為0.998 7，滿足3σ設計要求，轉換系數均值和方差對可靠度的影響最為明顯。