高比表面積周期性多孔結構拓撲優化*

杜義賢，羅明亮，付君健,2，田啟華，周祥曼，孫鵬飛

(1.三峽大學機械與動力學院，湖北 宜昌 443002；2.水電機械設備設計與維護湖北省重點實驗室，湖北 宜昌 443002)

0 引言

周期性多孔結構是功構一體化的優良載體，具有高比表面積、高比剛度、高比強度、隔熱、隔音等特性[1-2]。在電化學和生物工程領域，周期性多孔結構比表面積大小對結構性能具有重要影響。例如，在鋰電池領域，電極中含有多孔式的集流體結構，其表面包覆有活性材料，集流體結構比表面積大小決定活性材料的分布[3]，對鋰離子擴散系數、電子導電率、鋰離子存儲空間有重要影響。在化學工程領域，為了增大催化劑與反應物的接觸面積，多孔催化劑載體結構需要有較高的比表面積[4]。在生物工程領域，較高比表面積和合適孔徑大小的骨支架有利于細胞在其中生長[5]。因此，比表面積大小是周期性多孔結構重要的工程設計參數。拓撲優化通過調控結構的參數，將結構參數與性能聯系起來[6]，從而獲得高比表面積的拓撲構型。

拓撲優化是周期性多孔結構的重要設計方法[7]。通過施加周期性邊界條件約束，拓撲優化可在設計域內尋找滿足目標函數和約束條件的最優材料分布[8]。提高周期性多孔結構比表面積的拓撲優化設計方法可分為兩類：一類是基于均勻化[9-10]的設計方法；另一類是基于宏觀周期性約束的設計方法[11]。例如，采用均勻化法計算復合材料的性能參數，實現單胞內材料的重新分配[12]，有效提高了周期性多孔結構的比表面積；在單一體積約束下，基于能量均勻化法，對結構等效屬性評價[13]，可得到具有高比表面積的周期性多孔結構。但是，采用均勻化方法進行高比表面積周期性多孔結構設計，其尺度分離假設會帶來微結構單胞間材料不連通的問題，不具備制造性。此外，將宏觀設計域分解為若干子區域，利用子結構凝聚構建超單元計算模型減少有限元計算量[14-15]，組裝子結構可得到高比面積周期性多孔結構。對宏觀周期性多孔結構的最大尺寸進行限制，可進一步提高其比表面積。然而，基于宏觀周期性約束的高比表面積多孔結構設計方法存在大量約束問題，不便于計算。

本文提出了一種高比表面積周期性多孔結構拓撲優化方法，引入局部體積約束，使設計域內材料進一步分散，顯著提高了結構的比表面積。通過p-norm函數將多體積約束凝聚為單一體積約束，解決了宏觀周期性約束產生的大量約束問題，提高了拓撲優化的求解效率。數值算例驗證了本文方法的有效性。

1 周期性多孔結構的定義

本文采用宏觀周期性約束方法，將整體設計域劃分為若干個相同大小的子區域，如圖1所示。所有子區域中相同位置單元的相對密度保持一致，從而使各子區域具有相同的拓撲形式，以保證結構的周期性[11]。各單元密度關系的數學表達式為：

x1,j=x2,j=…=xm,j
xi,j∈[0,1](i=1,2,…,m;j=1,2,…,n)

(1)

式中，xi,j為設計變量，表示第i個子區域內第j個單元的密度；m為總設計域劃分的子區域個數，n為子區域內單元數量。

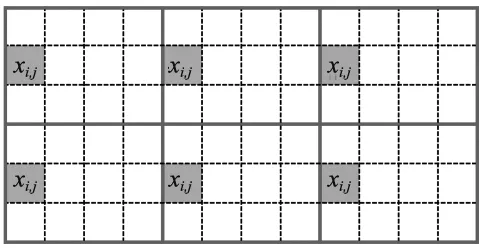
圖1 二維周期性結構設計域

2 局部體積約束

假定拓撲優化設計域內材料分布由邏輯值ρe表示，ρe=1或0代表實體單元或孔洞單元。為了限制設計域內材料積累形成大的實體區域，引入局部體積約束使設計域內材料進一步分散。

(2)

(3)

圖2 局部體積約束

(4)

(5)

式(5)可重新寫為：

(6)

式中，N是整體設計域內單元總數量。p越大，每個單元的約束就越強，同時也增加了問題的非線性。

引入一個數值從0～1連續變化的單元密度xe作為拓撲優化設計變量，為去除中間密度單元產生的棋盤格現象[17]，通過局部濾波器計算相鄰單元的加權平均值對xe過濾：

(7)

(8)

式中，re為敏度過濾半徑，其數值小于圖2中集合Ne的半徑RΩ；oi和oe為單元中心；式(7)中權重因子Wi,e大小和oi、oe兩單元中心距離有關：

(9)

(10)

式中，參數β控制閾值函數斜率，如圖3所示。當β越大時，函數值越接近0或1。如果直接應用一個較大β值，會導致高度非線性解；因此，本文從β=1開始迭代，經過一定迭代次數后，將其數值翻倍，這個過程稱為參數擴展，可提高優化求解的收斂性[18]。

圖3 不同參數β控制的Heaviside函數

3 拓撲優化數學模型

基于改進固體各向同性(Modified Solid Isotropic Material with Penalization, modified SIMP)的變密度法材料插值模型[19]，建立單元楊氏模量Ee數學表達式：

(11)

式中，E0為實體單元剛度值；Emin為一非常小的數值，代表孔洞單元剛度值，以防止整體剛度矩陣產生奇異值；γ為單元密度的懲罰因子，對拓撲優化中具有中間密度的單元進行懲罰，使其收斂于指定的密度上下界，從而抑制灰度單元。任意單元剛度矩陣Ke為：

Ke=Ee(ρe)k0

(12)

式中，k0為實體單元剛度矩陣。

引入局部體積約束對設計域內的材料分布進行限制，基于改進SIMP插值模型，以單元相對密度xe為設計變量，構造多孔結構周期性約束條件，以結構剛度最大化為優化目標，建立拓撲優化數學模型：

find:xe= {x1,j,x2,j,x3,j,…,xi,j}

(i= 1,2,…,m;j= 1,2,…,n)

(13)

式中，c、K、U、F分別為整體柔度、剛度矩陣、位移向量、載荷向量；g(x)為局部體積約束方程，控制結構比表面積大小。

4 敏度分析

基于式(13)的拓撲優化數學模型，以單元相對密度xe為設計變量，采用有限元移動漸近線方法[20](Method of Moving Asymptotes, MMA)來更新設計變量，需要分別計算目標函數柔度c和局部體積約束方程g(x)對設計變量xe的一階導數，用鏈式法則計算如下：

(14)

(15)

由式(11)、式(13)得：

(16)

式(14)、式(15)中其他部分導數為：

(17)

(18)

(19)

(20)

為保證式(13)中每個子區域第j個單元的密度相等，需要對敏度平均：

(21)

5 數值算例

本文采用懸臂梁和Michell梁拓撲優化算例，分別計算和對比有、無局部體積約束的周期性多孔結構表面積，驗證本文提高結構比表面積方法的有效性。在三維空間中，比表面積是指多孔結構單位質量所具有的孔洞總面積[21]，可定義為：面積/體積；在二維平面中，比表面積是指多孔結構單位面積所具有的孔洞總周長，可定義為：長度/面積。材料彈性模量E=1，泊松比u=0.3，單元大小默認為1(所有單位均為無量綱值)，以結構剛度最大為目標建立優化模型，采用MMA算法進行求解。

5.1 懸臂梁

圖4所示為懸臂梁結構，其設計域豎直方向和水平方向的長度分別為：H=100，L=200。左側邊界固定，右側邊界中間節點加載一豎直向下的集中載荷F。有限元單元為四節點矩形單元，采用200×100網格離散設計域，劃分為4×2大小的子區域，總體體積分數為0.45。

圖4 懸臂梁結構的設計域示意圖

取局部體積分數上限α=0.6，有、無局部體積約束的周期性多孔結構對比如圖5所示，其迭代過程如圖6所示。

(a) 無局部體積約束 (b) 有局部體積約束圖5 懸臂梁拓撲優化結構對比圖

(a) 無局部體積約束 (b) 有局部體積約束圖6 懸臂梁拓撲優化迭代曲線

由圖5可以得出，無局部體積約束的結構桿件較為粗壯；有局部體積約束的結構最大尺寸減小，拓撲優化構型細節特征增加，孔徑變小，孔洞數量增多。圖6為懸臂梁拓撲優化迭代曲線，圖6a為無局部體積約束的迭代曲線，整個優化過程收斂平穩，目標函數柔度c最終收斂于129；圖6b給出了局部體積分數上限α=0.6、p-norm函數控制參數p為16時的迭代曲線，Heaviside函數控制參數β每迭代40次數值翻倍，因而目標函數每隔40步會出現短暫的波動，目標函數柔度c最終收斂于173。因此，對比有、無局部體積約束的周期性結構拓撲構型可以得出，有局部體積約束的結構細桿特征增加，結構柔度變大，實現了最大尺寸約束，具有更高的比表面積。

因周期性多孔結構每個單胞完全一樣，為減少計算量，測量、對比其單胞的表面積即可。拓撲優化原始構型存在孔洞邊緣“模糊”、表面不光滑的問題，往往不能直接精確繪制其孔洞邊緣，從而無法準確測量比表面積。為解決該問題，采用水平集方法(Level Set Method)[22-23]對周期性多孔結構的原始單胞進行后處理。以單胞拓撲構型圖的像素為單位測量孔洞總周長，即為表面積，結果見表1。在懸臂梁算例中，具有局部體積約束的拓撲構型比表面積(比表面積與表面積成正比)提高了約300%，驗證了本文方法的有效性。

表1 懸臂梁單胞拓撲構型對比

5.2 Michell梁

圖7所示為Michell梁結構，其設計域豎直方向和水平方向的長度分別為：H=100，L=200。左側邊界底部為簡支支撐，右側邊界底部為固定支撐，底部中間加載一豎直向下的集中載荷F。有限元單元為四節點矩形單元，采用200×100網格離散設計域，劃分為4×2大小的子區域，總體體積分數為0.45。

圖7 Michell梁結構的設計域示意圖

取局部材料體積分數上限α=0.6，有、無局部體積約束的周期性多孔結構對比如圖8所示，其迭代過程如圖9所示。

(a) 無局部體積約束 (b) 有局部體積約束圖8 Michell梁拓撲優化結構對比圖

(a) 無局部體積約束 (b) 有局部體積約束圖9 Michell梁拓撲優化迭代曲線

由圖8可以得出，在Michell梁算例中，有局部體積約束的周期性拓撲構型具有更多的細節特征，孔洞數量增多。圖9 Michell梁拓撲優化迭代曲線中，無局部體積約束的周期性結構柔度c最終收斂于28；有局部體積約束的周期性結構柔度c最終收斂于32。因此，有局部體積約束的結構細桿特征增加，結構柔度變大，實現了最大尺寸約束，具有更高的比表面積。單胞拓撲構型及表面積大小具體見表2。在Michell梁算例中，本文提出的局部體積約束方法將拓撲構型的比表面積提高了約200%，驗證了該方法的有效性。

表2 Michell梁單胞拓撲構型對比

6 結論

本文提出了一種高比表面積周期性多孔結構拓撲優化方法，通過引入局部體積約束，使設計域內材料進一步分散，對周期性多孔結構的最大尺寸實現了有效控制，顯著提高了結構的比表面積。通過p-norm函數將多體積約束凝聚為單一體積約束，解決了局部體積約束產生的大量約束問題，提高了拓撲優化的求解效率。使用水平集方法對周期性結構單胞進行后處理，得到光滑邊界的拓撲構型，從而在數據分析軟件中精確測量了結構的表面積。拓撲優化經典二維數值算例驗證了本文方法的有效性。