徑向浸入率通用型銑削穩定性譜元分析法*

謝建宏，徐菁菁,b，張 宇，李 鳴

(南昌大學 a.信息工程學院；前湖學院，南昌 330031)

0 引言

銑削穩定性是指銑削系統和切削過程相互作用構成的整體系統的穩定性，其實質是描述刀具與工件的相對振動[1]。銑削過程失穩即發生銑削顫振，刀具與工件間產生大幅振動甚至脫離，使得工件加工精度和表面質量超差并顯著加劇刀具磨損，同時伴隨工作環境極度惡化，甚至造成機床損壞和生產安全事故。保守地選擇切削參數雖然能避免發生顫振，卻極大地降低了加工效率。因此，對銑削穩定性的準確、高效分析是保證銑削加工質量和效率的關鍵。考慮切厚再生效應的銑削過程動力學模型較好地描述了顫振機理并得到了大量實驗驗證[2]。該模型將銑削過程表征為一組周期系數時滯微分方程，其特征方程是超越方程,這給穩定性分析帶來了本質性困難[3]。Altintas等開創性地提出了基于Lyapnov判據的單頻率法,由此構建了臨界切削參數表征的銑削穩定性葉瓣圖(Stability Lobe Diagrams, SLDs)以區分穩定切削參數域與不穩定切削參數域[4]。Insperger T等提出了基于Floquet判據的半離散法，具有比單頻率法更好的準確性和通用性，成為當前的主流分析方法[5]。此類分析方法的計算瓶頸在于微分方程離散狀態向量映射矩陣的獲取。針對此問題，國內外研究者提出了許多近似計算方法以提高計算效率從而快速構建SLDs的葉瓣邊界[6-9]。基于譜方法和時間有限元法相結合的譜元法給出了一種效率顯高于傳統半離散法的分析方法[10]，然而大量工程實踐發現經典譜元法對于小徑向浸入率銑削工況適用性較差，其原因主要在于刀齒切入切出引起的銑削過程強不連續性降低了譜元的收斂性，從而極大地影響了計算效率[11]。

本文提出一種徑向浸入率通用型譜元法，將銑削過程時滯周期劃分為切削振動和自由振動兩個時間段分別進行處理。利用譜元法與微分方程數值解法相結合解決小徑向浸入率銑削的強不連續性問題，提高狀態向量離散映射矩陣的計算效率，進而保證銑削穩定性分析的準確性、高效性和通用性。

1 銑削穩定性譜元分析方法原理

1.1 銑削過程動力學狀態空間模型

經典銑削穩定性分析采用基于再生型動態銑削力模型和銑削工藝系統動力學特性建立的二自由度周期系數時滯微分方程組描述銑削過程動力學，其狀態空間模型如式(1)所示：

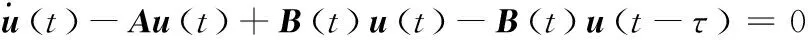
(1)

式中，τ為時滯周期，在N齒等齒矩銑刀以主軸轉速Ω[rpm]銑削的工況下取為一個刀通周期τ=T=60/NΩ，式中狀態變量和系數矩陣表達式分別為：

(2)

狀態向量u(t)為X,Y方向位移與速度構成的列向量，M,K,C分別表示銑削系統質量、剛度、阻尼矩陣，H(t)表示動態銑削力系數矩陣，如式(3)所示：

(3)

式中，a為軸向切深，Kt為切向切削力系數，Kr為徑向與切向切削力系數之比，s表示sin(2φj)，c表示cos(2φj)。瞬時浸入角φj=(2πΩ/60)t- (j- 1)2π/N，j=1,…,N。g表示階躍函數：

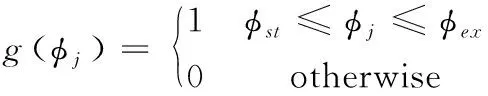
(4)

切入角φst和切出角φex由徑向浸入率決定，g(φj)反映了刀齒是否正參與切削。可見，式(1)中，A是常系數矩陣，B(t)是以T為周期的周期系數矩陣。

Floquet穩定性判據依據銑削過程動力學模型在一個周期上的離散狀態映射矩陣的特征乘子在Z平面的分布進行銑削過程判穩：若特征乘子都位于單位圓內則銑削過程穩定，否則發生顫振。

1.2 銑削穩定性分析的經典譜元法

經典譜元法將[-τ,τ]時間線劃分為2M個時域譜元，每個譜元長h=τ/M，如圖1所示。

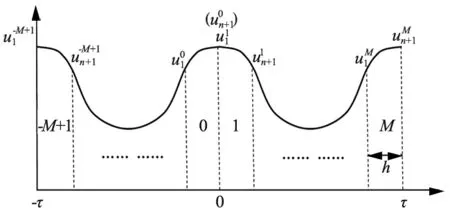
圖1 經典譜元法時間線劃分

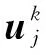
(5)

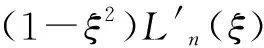
(6)

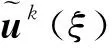
(7)

式(6)回代式(1)，采用加權余量法即可導出一個周期上離散狀態向量的映射關系，進而計算離散狀態向量映射矩陣特征乘子并根據Floquet判據判別銑削穩定性。由于采用了LGL節點高階譜插值，使得譜元法相較采用等距節點插值和均值近似的傳統半離散法具有更高的計算效率。然而對于小徑向浸入率銑削，由于刀齒切入和切出導致H(t)具有強不連續性，使得加權余量法計算過程中LGL數值積分的收斂速度和精度都明顯下降，影響了經典譜元法對小徑向浸入率銑削的適用性。

2 徑向浸入率通用型銑削穩定性譜元分析法

消除刀齒切入切出不連續性影響的一種思路是將圖1按銑削過程劃分為切削振動時段tc和自由振動時段tf分別求解式(1)，如圖2所示。基于此思路提出一種徑向浸入率通用型銑削穩定性譜元分析方法。

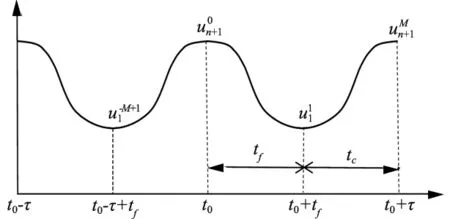
圖2 徑向浸入率通用型譜元法時間線劃分

式(1)解可描述為積分形式：

(8)

式中，u(t0)為初始時刻t0的狀態向量值。不失一般性，設t0為刀具切出時刻，在自由振動區間[t0,t0+tf]不存在切厚再生效應，式(8)中B(η)項為0，退化為無時滯常系數微分方程齊次解形式，得式(9)：

u(t)=eA(t-t0)u(t0)

(9)

解得刀具切入時刻狀態向量為：

u(t0+tf)=eA(tf)u(t0)

(10)

在切削振動區間[t0+tf,t0+τ]，存在切厚再生效應使B(η)項不為0，在此區間及上一周期區間 [t0+tf-τ,t0]上分別以時間段h=tc/M等距劃分譜單元并將時間坐標t∈[(k-1)h,kh]規范化為[-1,1]區間局部坐標ξ，采用式(6)插值近似，導出kth譜單元上方程余量為：

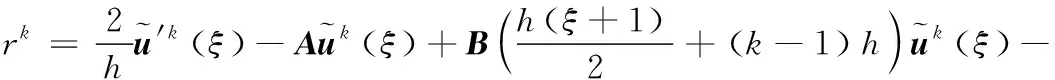
(11)

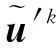
(12)

式中，

(13)

(14)

權函數ψi(ξ)取Legendre正交多項式函數族：

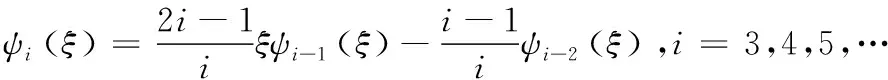
(15)

采用LGL數值積分計算式(13)、式(14)得：

(16)

(17)

式中，I表示4×4單位陣，lj′(ξ)表示重心Lagrange插值函數對ξ的一階導。wj為LGL數值積分系數，如式(18)，其中Ln表示n階Legendre多項式。

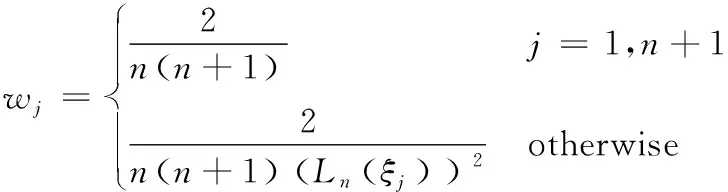
(18)

可見，n+1點LGL數值積分具有2n+1階代數精度，相較Newton-Cotes積分極大提高了計算精度，且避免了傳統等距節點高階插值的Runge現象導致系統病態無法實現譜收斂的問題。

綜合考慮自由振動時段和切削振動時段，將式(10)和式(12)相結合，即可導出銑削過程一個時滯周期上離散狀態向量的映射關系：

NUτ=PU0

(19)

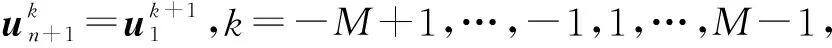
(20)

(21)

(22)

則式(1)在一個時滯周期上的離散狀態向量映射矩陣Φ為：

Φ=N-1P

(23)

求解矩陣Φ的特征值，根據Floquet穩定性判據即可分析銑削過程穩定性，并據此繪制銑削穩定性葉瓣圖。

3 仿真驗證

3.1 仿真設置

為驗證本文所提算法的準確性、高效性和通用性，針對表1所示相同工藝參數、結構參數、材料參數的二自由度銑削過程動力學模型分別使用徑向浸入率通用型譜元法和經典譜元法進行銑削穩定性分析，不失一般性地假設銑削工藝系統動態特性在X,Y方向對稱且互不耦合，即式(2)中M,M-1K,M-1C分別退化為對角陣mI,ωn2I, 2ζωnI, 其中m,ωn,ζ分別表示銑削工藝系統的模態質量、固有頻率和阻尼比。所有算例均在HP-ZBOOK15G3移動工作站(Core i7 6700hq處理器, 32 GB內存, QUADRO M1000M GPU)上完成。

3.2 仿真結果與分析

圖3展示了徑向浸入率取1、 0.2、0.05時，分別采用經典譜元法和徑向浸入率通用型譜元法進行銑削穩定性分析獲取的銑削穩定性葉瓣圖，表2給出了兩種分析方法仿真銑削穩定性葉瓣圖的計算時間對比。可見，在最大分析誤差不超過1%的前提下，徑向浸入率通用型譜元法在大浸入率工況下具有與經典譜元法相同的計算效率，但在小浸入率工況下計算效率則明顯高于經典譜元法，這是由于其較好地處理了銑削力方向系數的不連續性，使得采用較低的譜元階次即可實現SLDs曲線收斂到準確值。圖4和圖5分別展示了徑向浸入率為0.1的順銑過程穩定性葉瓣圖的經典譜元法和徑向浸入率通用型譜元法的收斂情況。對比結果表明對于小徑向浸入率銑削，經典譜元法收斂效率明顯降低，當譜元階次取60時葉瓣圖基本收斂，而徑向浸入率通用型譜元法在譜元階次取25時已經收斂到準確值，且譜元插值計算僅需在切削振動段進行，進一步縮小了計算區間，極大提高了計算效率，使得算法具有更強的工況通用性。

表1 銑削穩定性仿真算例參數

表2 兩種銑削穩定性分析方法的計算效率對比

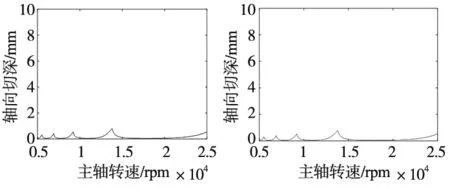
(a) 徑向浸入率= 1經典譜元法 (b) 徑向浸入率= 1徑向浸入率通用型譜元法

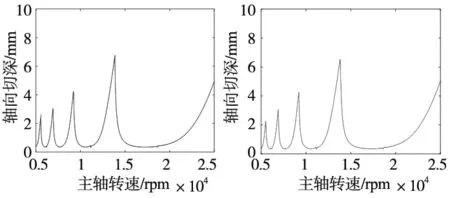
(c) 徑向浸入率= 0.2經典譜元法 (d) 徑向浸入率= 0.2徑向浸入率通用型譜元法

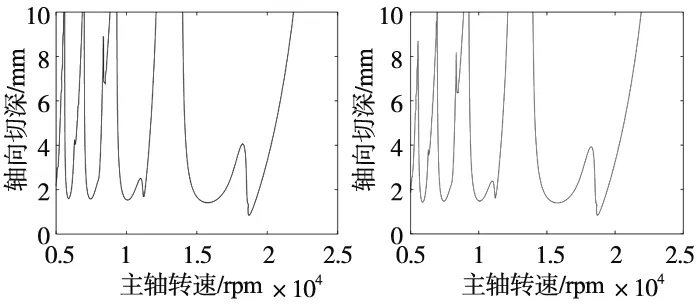
(e) 徑向浸入率= 0.05經典譜元法 (f) 徑向浸入率= 0.05徑向浸入率通用型譜元法圖3 經典譜元法和徑向浸入率通用型譜元法銑削穩定性葉瓣圖仿真結果對比

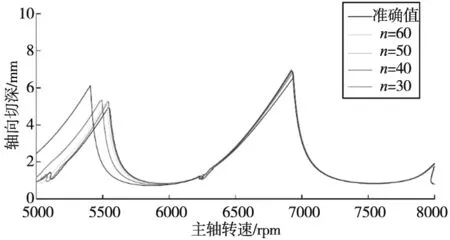
圖4 經典譜元法穩定性葉瓣圖收斂情況

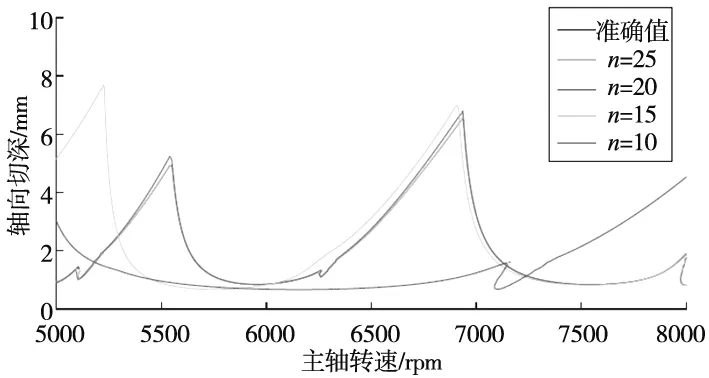
圖5 徑向浸入率通用型譜元法穩定性葉瓣圖收斂情況

4 結論

本文闡述了一種用于銑削過程穩定性分析的徑向浸入率通用型譜元法，并針對經典銑削工況進行了穩定性葉瓣圖仿真，結果表明該方法通過將LGL節點高階譜元與微分方程數值解法相結合，較好解決了小徑向浸入率銑削強不連續性導致的譜元收斂效率降低的問題。在分析誤差不超過1%的前提下，相較經典譜元法顯著提高了計算效率，實現了大/小徑向浸入率銑削工況穩定性分析的強通用性，使無顫振銑削參數在線優化成為可能。