低雷諾數下附屬棱柱的圓柱繞流減阻

趙 強， 蔣光彪， 胡江濤

(中南林業科技大學土木工程學院工程流變學湖南省重點實驗室， 長沙 410000)

繞流問題一直是流體力學領域最經典的問題之一，與許多實際工程問題息息相關，如海洋平臺、深海管道、高空線纜、超高層建筑物、橋梁結構等，相關各個工程領域必須考慮流體經過時造成的渦激振蕩對其結構穩定性的影響，以降低事故風險，減少經濟損失。因此，相關減阻措施的研究[1-2]受到科研人員普遍關注。

目前，采用擾流體措施對圓柱力學性能的影響已有不少研究成果，其中擾流體多采用分隔板[3-5]、控制桿等，研究不同位置下擾流體對圓柱升力、阻力系數和斯特勞合爾數(St)造成的影響。Gim等[6]通過實驗研究了在圓柱后滯點放置不同尺寸的附屬桿對圓柱尾流的控制，得出了近尾跡區內能較好地抑制漩渦形成的結論。Silva-Ortega等[7]實驗研究了雷諾數在5 000～50 000時圓柱周圍設置2、4、8根控制小圓柱，得出設置4根控制桿的減阻效果最好，其阻力系數較單圓柱最大可以降低約50%的結論。Lu等[8]通過數值模擬研究了層流下圓柱附加多根小直徑圓柱時對其升力、阻力的抑制情況，發現6根控制桿時對不同攻角的降力表現出更好的性能。Song等[9]數值模擬了附3根控制桿圓柱的層流流動，研究了不同攻角、間距比對流體力、頻率和流場等的影響。Wu等[10]研究了圓柱下游設置單根圓柱在小間隙比下對其渦激振動有決定性影響。在其他被動減阻措施中，研究較多的有對圓柱表面形狀的修正[11]、設置O型環[12]、開展向槽[13]、開貫通狹縫[14-15]等。

現將一對對稱布置的等邊三棱柱設為擾流柱，在固定長徑比(棱柱邊長與圓柱直徑比)下研究其不同位置下對主圓柱力學性能的影響。經廣泛查閱文獻，發現中外對層流下以三棱柱作為擾流柱的圓柱繞流減阻研究非常少見，為此將通過Linux系統下開源的計算流體動力學(computational fluid dynamics，CFD)平臺OpenFOAM進行數值模擬，分析低雷諾數下設置附屬棱柱對圓柱升力、阻力和渦脫頻率的影響，開展相關減阻性能研究。

1 控制方程

層流下二維不可壓縮黏性牛頓液體的運動規律可采用Navier-Stokes方程來描述，即

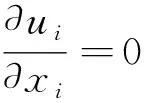
(1)

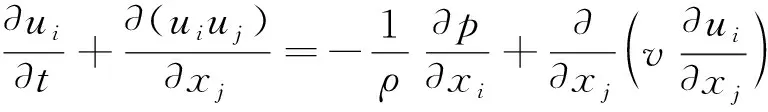
(2)

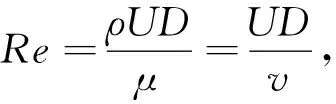
2 數值模擬

2.1 流場計算域及網格劃分

物理模型如圖1所示，圖1(a)為圓柱上游設置的一對對稱附屬擾流棱柱(簡稱“擾流柱”)，圖1(b)為圓柱下游設置的一對對稱擾流柱，圓柱直徑為D，棱柱為邊長d的等邊三棱柱，三棱柱中點到圓柱圓心O的距離為L，兩棱柱與x軸的夾角均為θ(0°≤θ≤90°)。

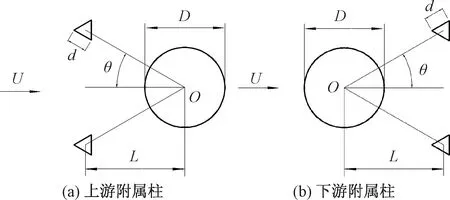
圖1 擾流柱位置示意圖Fig.1 Schematic diagram of position of pin fins

圓柱繞流數值模擬計算域的劃分如圖2所示，流向長度(x軸方向)為37D，橫向寬度(y軸方向)為30D，圓柱距入流口12D，距出流口25D。圓柱直徑D=0.1 m，入口為均勻定常來流，流速為 0.1 m/s。計算域上下邊界均為對稱邊界，入口設為速度入口邊界，出口設為壓力出口邊界，圓柱和擾流柱表面均采用無滑移邊界條件。

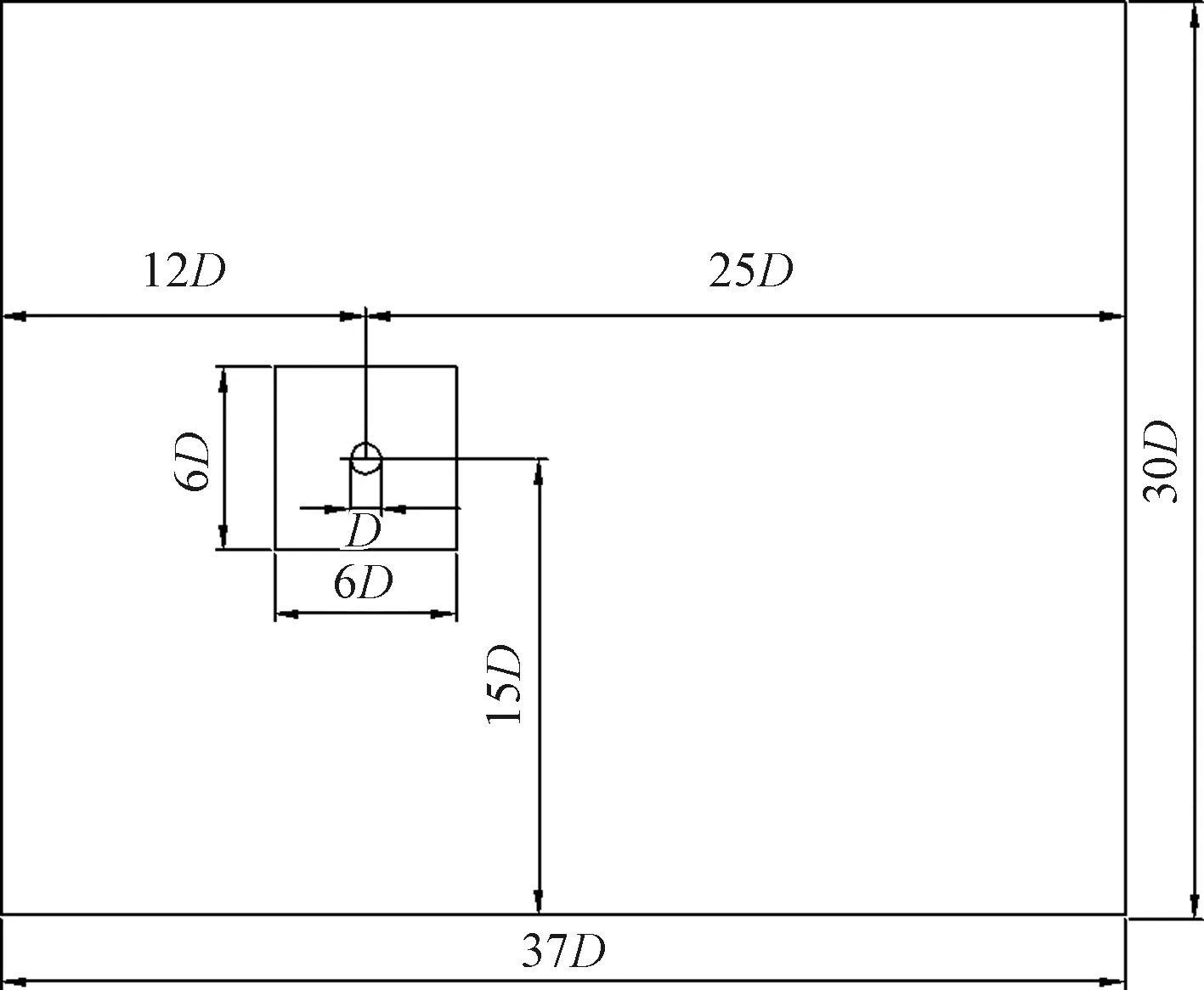
圖2 計算域示意圖Fig.2 Sketch map of computational domain

計算域網格劃分采用GAMBIT進行劃分，如圖3所示，采用分區劃分網格，圓柱四周劃分較密集結構化網格，遠離圓柱區域按比例疏化網格。當布置擾流棱柱時，難以全部使用結構化網格，則采用棱柱與圓柱的區域布置非結構化網格，其他區域均采用結構化網格。圓柱壁面網格節點均勻剖分160個，附屬棱柱邊劃分30個節點，網格局部放大圖如圖4所示。不設擾流柱總單元網格數為18 040，設擾流柱總單元網格平均數為22 703。

圖3 計算域全局網格Fig.3 The whole mesh of domain

圖4 圓柱周圍網格細節Fig.4 Mesh in the vicinity of the cylinder

2.2 模型驗證

為驗證計算域網格劃分、模型設計和求解參數設置的準確性，結合前人實驗和其他數值模擬結果，對Re=200單圓柱繞流工況下模擬結果數值進行對比分析，結果如表1所示。采用OpenFOAM數值模擬得到Re=200的單圓柱繞流流場在200 s時間段內阻力系數和升力系數歷程如圖5所示。

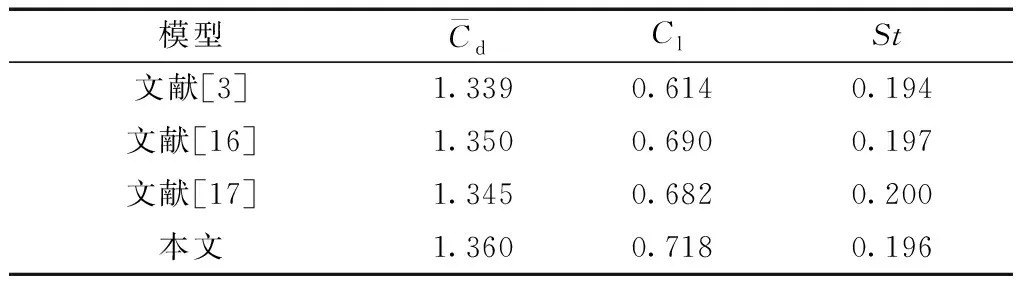
表1 單圓柱繞流結果對比

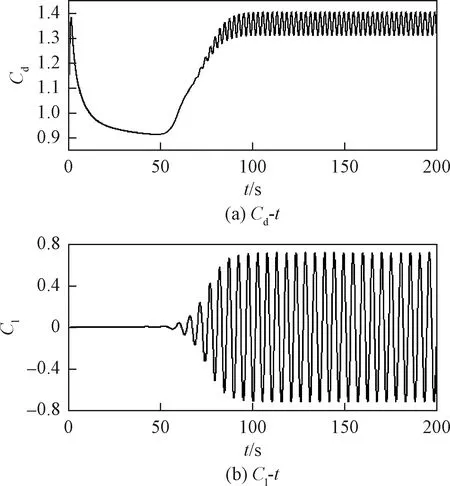
圖5 單圓柱阻力系數、升力系數隨時間的變化曲線Fig.5 Variation of drag and lift coefficients as a function of time of a single cylinder

3 結果分析

3.1 上游擾流棱柱數值模擬

采用上游設置一對擾流柱，物理模型如圖1(a)所示，擾流柱為邊長為d的等邊三棱柱，d/D=0.25，在Re=200時研究其設置在不同角度θ和不同距離L對圓柱升力和阻力系數的影響規律。利用OpenFOAM計算了三組不同角度工況下，主圓柱受力和渦脫頻率與間距L的變化規律，計算結果如圖6所示。

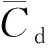
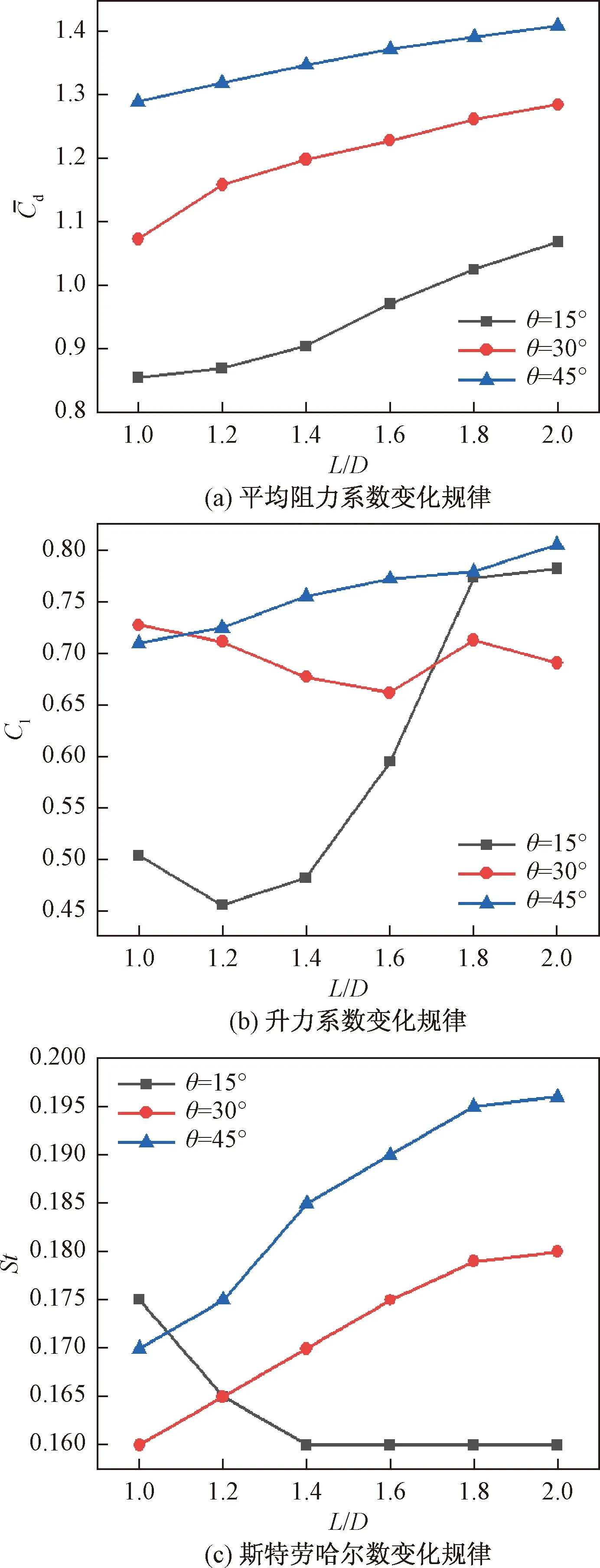
圖6 前置擾流柱時Cl、St隨L/D的變化規律Fig.6 Variation of Cl and St as a function of L/D with the front pin fins

圖7所示為θ=15°、L/D=1.0時，圓柱正向升力系數達到最大時其表面壓力系數變化曲線圖。

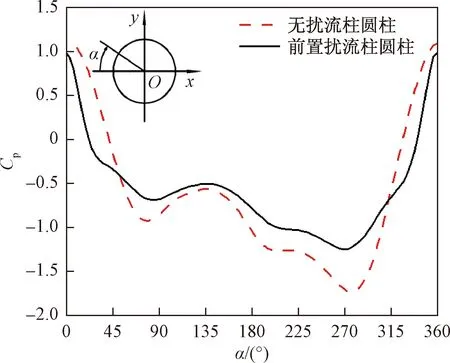
圖7 前置擾流柱圓柱表面壓力系數(Cp)分布圖Fig.7 Distribution of surface pressure coefficient on the cylinder with the front pin fins

通過和單圓柱表面壓力系數對比，不難發現圓柱前后表面壓力系數絕對值均得到了明顯降低，而前后壓差阻力的減小則是圓柱阻力系數降低的關鍵原因，同時也可以發現圓柱上下表面的壓力系數差值也得到了降低，從而使得升力系數減小但不為零。

3.2 下游擾流棱柱數值模擬

物理模型圖1(b)所示，該部分研究采用在參考圓柱下流處布置一對擾流等邊三棱柱，d/D=0.25，在雷諾數Re=200時分析不同夾角θ和間距L對圓柱受力的影響規律。采用與上流布置擾流柱同樣的模擬方法進行模擬，計算結果如圖8所示。

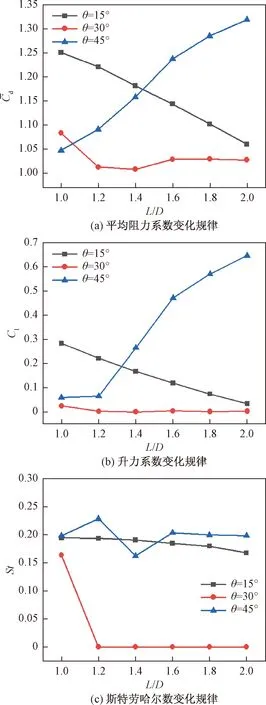
圖8 后置擾流柱時Cl、St隨L/D的變化規律Fig.8 Variation of Cl and St as a function of L/D with the rear pin fins

圖9所示為θ=30°，L/D=1.4，Re=200下圓柱正向升力系數達到最大時其表面壓力系數變化曲線圖。可以看出，圓柱后方的壓力系數絕對值得到了顯著降低，圓柱前后壓差減小，使得阻力系數得到降低。同時可以發現圓柱上下端壓力系數基本相等，可以得出圓柱的升力系數降低至接近于零。

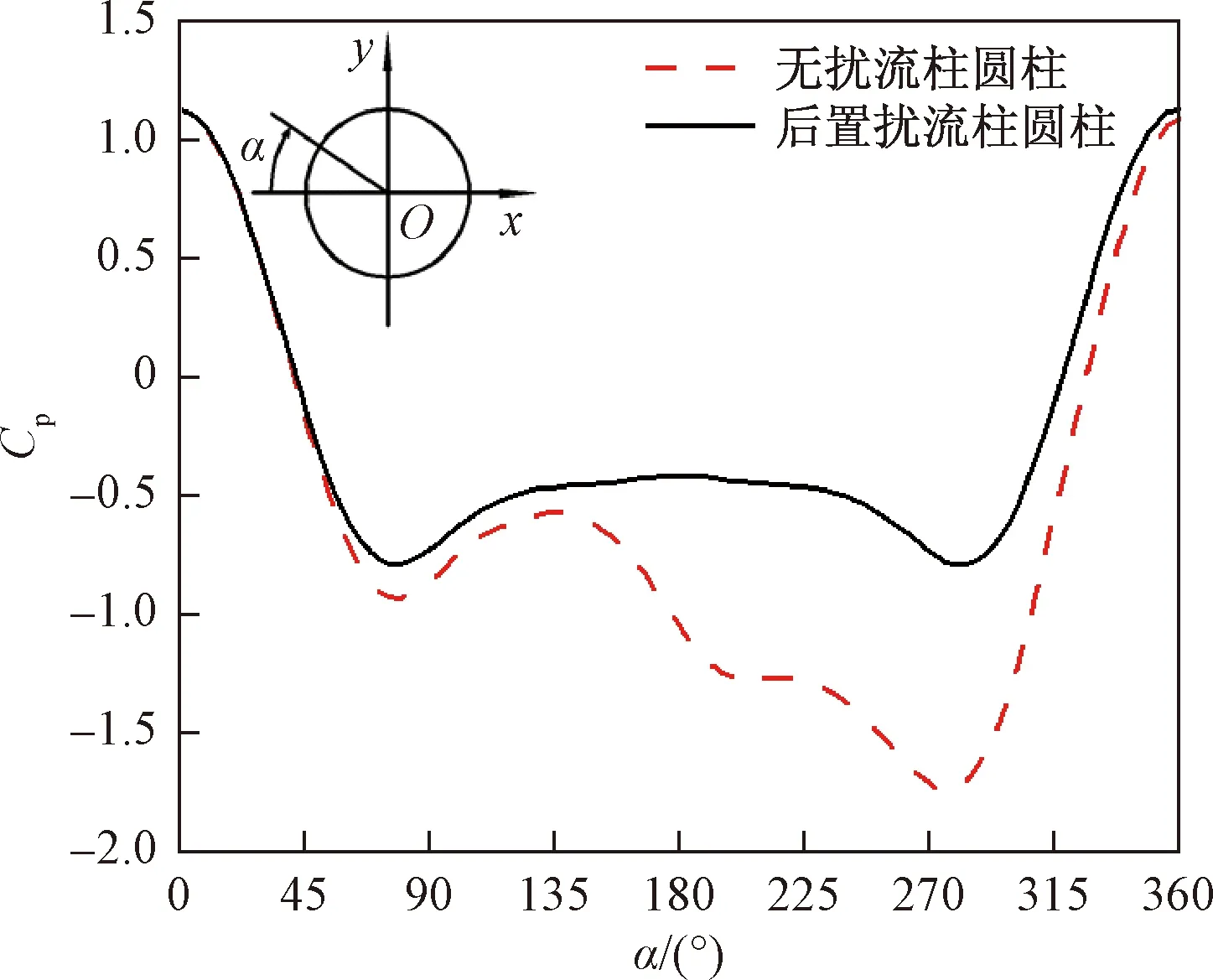
圖9 后置擾流柱圓柱表面壓力系數分布圖Fig.9 Distribution of surface pressure coefficient on the cylinder with the rear pin fins

3.3 主圓柱升力系數減小機理分析

圖10、圖11所示分別為圓柱前置、后置擾流柱時，在θ=15°、30°、45°下L/D為1.0和1.4時的渦量圖以及用于對比的無擾流柱單圓柱渦量圖。

圖10 前置擾流柱不同位置的渦量變化Fig.10 Vorticity variation of front pin fins at different locations

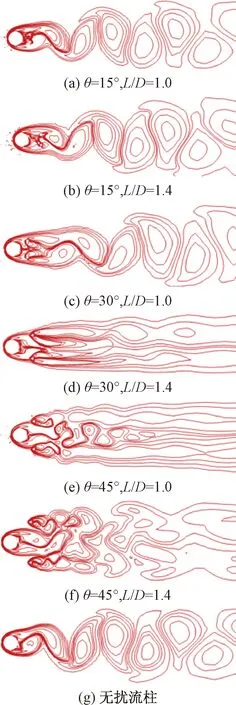
圖11 后置擾流柱不同位置的渦量變化Fig.11 Vorticity variation of rear pin fins at different locations

圖10為上游設置擾流柱時圓柱尾渦量圖，可以看出，對于單圓柱情況，圓柱尾跡區渦量圖呈現出不對稱性，這種周期性脫落的渦則是導致圓柱產生振動，從而使得升力系數呈現出大幅度振蕩的關鍵原因。而通過上流設置對稱擾流棱柱的措施，從渦量圖中可以看出對圓柱振動的抑制效果不太明顯，從前文數值模擬計算得出的升力系數變化規律圖中也不難發現，僅當θ=15°、擾流柱距圓柱體較近時對升力系數振蕩的幅值有一定控制效果，渦量圖中則表現為在相同長度的尾跡區內渦脫落個數的減少。圖11為圓柱下游設置擾流柱對主圓柱尾渦量的影響，不難發現，在θ=15°時，尾渦脫落的控制效果不太明顯，整個渦量圖不對稱感強烈。當θ=30°時，則可以發現較明顯的變化，L/D=1.0時第一個尾渦脫落的位置就得到了明顯的延后；L/D=1.4時整個尾跡區渦量圖的對稱性得到了明顯的改善，對照前文的數值模擬結果，此時圓柱上垂直升力基本為零，表現為升力系數曲線波動幅值接近零，圓柱振蕩反應也得到了充分的抑制。當θ=45°時，可以發現隨著擾流柱逐漸遠離圓柱，尾跡區渦量圖的對稱性開始減弱，升力系數幅值也逐漸增大。

綜上所述，在圓柱上游和下游位置設置擾流柱對圓柱周圍的流場特性有著不同的改善作用。對稱擾流棱柱布置在圓柱上游時對圓柱平均拖拽力的抑制效果更好，在θ=15°、L/D=1.0位置布置時達到最優效果，其垂向升力也能得到一定的減小；布置在圓柱下游時對圓柱垂向升力的抑制效果更好，在θ=30°、L/D=1.4位置布置時達到最優效果，其平均拖拽力也得到了降低，但效果不如上游布置好。

3.4 最優布置方案模擬

考慮到上下游各自布置擾流柱對圓柱受力和周圍流域影響有所不同，結合前文分析，擬采用前置擾流柱最佳降低圓柱平均拖拽力位置與后置擾流柱最佳降低圓柱垂向受力位置同時設置擾流柱方案，來分析圓柱受力情況，具體物理模型如圖12所示。

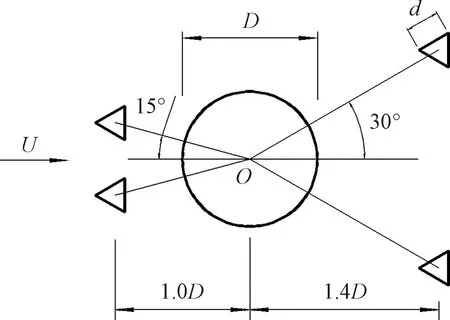
圖12 最優布置方案物理模型Fig.12 Physical model of optimal layout

圖12中圓柱直徑D=0.1 m，擾流柱邊長d/D=0.25，前置擾流柱布置在距圓柱1.0D、夾角θ=15°位置處，后置擾流柱布置在距圓柱1.4D、夾角θ=30°位置處。利用OpenFOAM對同時設置擾流柱方案在Re=200時模擬計算的阻力系數、升力系數時程變化如圖13所示。

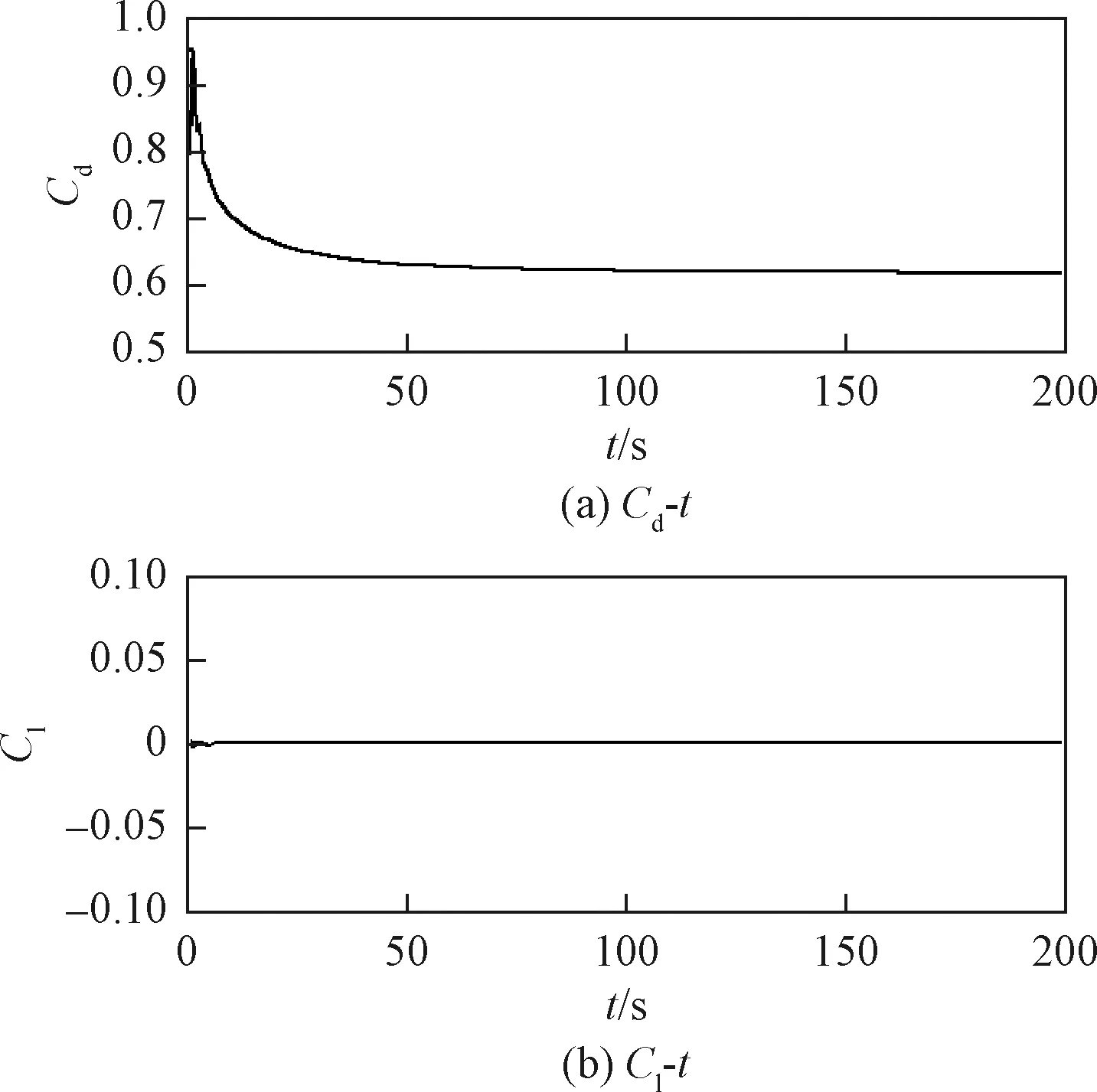
圖13 附屬4根棱柱下圓柱的阻力系數、升力系數變化曲線Fig.13 Variation of drag and lift coefficients of cylinder with four attached prisms

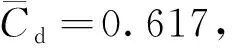
圖14為四根擾流柱布置下的壓力系數變化圖，通過與單圓柱最大正向升力系數時的壓力系數圖做對比，能直觀地反映出圓柱四周壓力系數的變化情況。圓柱前后壓差較大程度減小，上下端壓差降低至接近零，從而導致圓柱阻力系數、升力系數的大幅度降低。

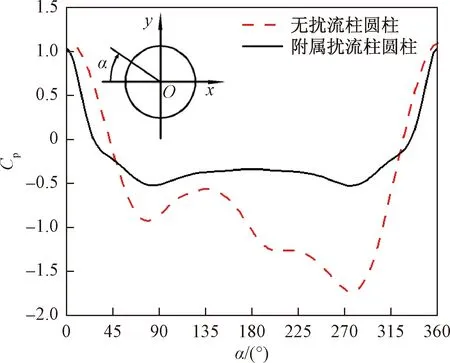
圖14 Re=200下圓柱表面壓力系數分布Fig.14 Distribution of surface pressure coefficient on the cylinderat Re=200

4 結論

(1)通過OpenFOAM多工況數值模擬研究表明，在圓柱上游或下游布置一對等邊三棱柱均能對圓柱表面的拖拽力和垂向升力起到一定的抑制作用。在上游區布置擾流棱柱能更有效地減小圓柱的阻力系數，當夾角θ=15°、L/D=1.0時平均阻力系數可降低至單圓柱情況下的62.79%；而在下游區布置擾流棱柱能更有效地減小圓柱的升力系數，當夾角θ=30°、L/D=1.4時圓柱的升力系數可降低至單圓柱情況下的0.14%。

(2)在進一步的研究中，采用上下游同時布置一對擾流棱柱對圓柱的受力情況進行分析，結果表明能夠融合上游、下游擾流柱各自改變圓柱受力的優勢，使得主圓柱的升力、阻力系數得到進一步的降低，其平均阻力系數可降低至單圓柱情況下的45.37%，升力系數可降低至單圓柱情況下的0.06%。