入庫徑流不確定條件下水庫多目標優化調度方案決策

王麗萍，吳月秋，張驗科，張 培

（1.華北電力大學水利與水電工程學院，北京102206；2.石家莊鐵道大學經管學院，石家莊050043）

長期以來，受徑流預報誤差的限制，水庫多目標優化調度研究大多是在確定性入庫徑流條件下開展的。由于未考慮入庫徑流等不確定的影響，防洪、發電、供水、航運等綜合利用效益有時難以有效發揮。隨著徑流預報技術的提高，預報精度越來越高，但預報誤差不可忽視，用預報值來指導實際運行的效益逐漸顯現，但是仍存在一定的風險性。因此，實際水庫多目標調度研究可以視為一個不確定、多維、連續、非線性的優化問題，既要考慮各種不確定性因素的影響，又要避免人為主觀因素的影響，這進一步加劇了調度決策的難度［1］。目前，可以應用于水庫多目標優化調度方案決策的方法較多，經典的方法有層次分析法，但該方法過于依賴于個體的主觀假設，忽略了實際問題的客觀性，評價結果有時會產生較大的偏差。因此，模糊集理論［2，3］、最大熵法［4，5］、灰色關聯法［6-8］等這些以數據的客觀性分析為主的方法逐漸受到眾多學者的青睞。近年來，一些新型的方法也逐漸涌現。例如，文獻［9］采用耦合均變率法和逼近理想點法來尋求水庫多目標優化調度的最佳均衡解，不受權重因子的影響，又可以對評價指標的定性和定量信息進行綜合考慮；文獻［10］建立了基于突變評價法的水庫調度多目標風險分析模型，避免了人為主觀進行權重賦值時對計算結果客觀性造成的不利影響；文獻［11］為了減小賦權過程中的模糊誤差，提出多維關聯抽樣的區間數灰靶決策模型，并應用于潘口水庫汛期運行水位抬升方案的決策；文獻［12］將投影尋蹤引入到溪洛渡-向家壩-三峽水庫蓄水方案的多目標決策中來；文獻［13］和［14］將多準則妥協解排序法（Vlsekriterijumska Optimizacija I Kompromisno Resenie，簡稱VIKOR）模型應用水庫多目標方案的決策中；文獻［15］引入水庫生態價值調度的概念，以探尋供水、發電、航運和生態的最佳決策方案；文獻［16］采用動態多目標差分進化算法進行風光水火多目標優化調度模型，并取得了最佳調度方案等。

然而上述方法一般都是在確定性來水條件下的多目標決策，決策時受主觀因素影響也較大。而實際調度過程中來水是不確定的，如何將這一不確定性加入到水庫多目標優化調度并得到合理的決策方案以指導實際調度決策是目前迫切要解決的問題。針對這一問題，本文一方面基于VIKOR模型不僅可以通過最大化群體效益和最小化個別遺憾使得各屬性之間彼此讓步而得到妥協解的特性，而且可以防止個別方案因距正負理想方案距離相同而無法判斷方案優劣的優勢；另一方面將區間數理論加入到評價模型當中來，將由于來水不確定而得到的各種評價指標值的信息充分表示出來，同時將博弈論法應用到主、客觀綜合權重的計算當中，從而探索入庫徑流不確定條件下的水庫多目標優化調度方案決策方法，豐富和完善水庫多目標調度決策的理論方法體系，為實際水庫多目標優化調度提供理論支撐。

1 基于區間數的評價指標的確定

在解決實際問題時，常常會遇到決策信息具有不確定性或模糊性，使得在對系統進行決策評估時，指標值難以精確化，評估者給出的指標值常常是區間數［17］。由于入庫徑流預報誤差的存在，且其具有不確定性，實際水庫多目標調度決策時各指標值選取區間數更能充分反映指標所包含的信息，區間數的上下限分別為指標值的最大值和最小值。對于各指標值區間的確定步驟如下：

（1）針對徑流實測和預報值，計算出各預見時刻的預報誤差，并量化其徑流預報誤差函數［18］。

（2）基于徑流預報誤差函數和實際徑流過程，采用蒙特卡洛法模擬K場預報徑流過程。

（3）依據這K場徑流過程進行水庫多目標優化調度計算，可以得到K組指標值，例如發電量、防洪風險率等。

（4）設有n個評價指標，m個多目標優化調度方案組成的非劣解集S={s1，s2，...sm}，對應的評價指標集可表示為A={a1，a2，...an}，方案si的指標屬性值為2，…，n），其中則評價指標矩陣A為：

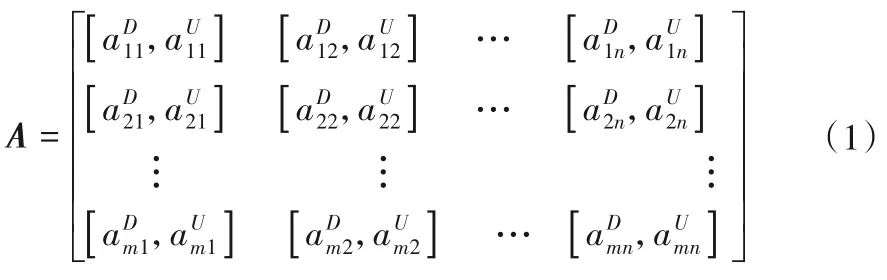
對A中各指標值進行標準化處理，首先把指標權重按照效益型指標和成本型指標進行劃分，具體標準化處理的公式如下：

效益型指標：

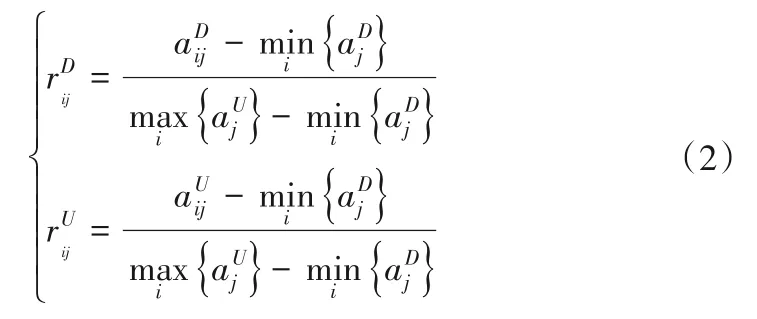
成本型指標：

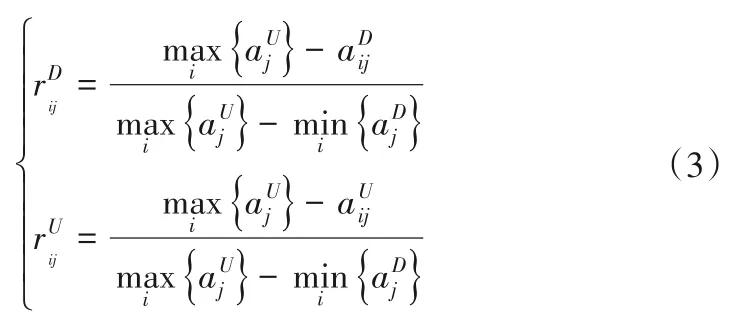
標準化處理后獲得決策矩陣R：

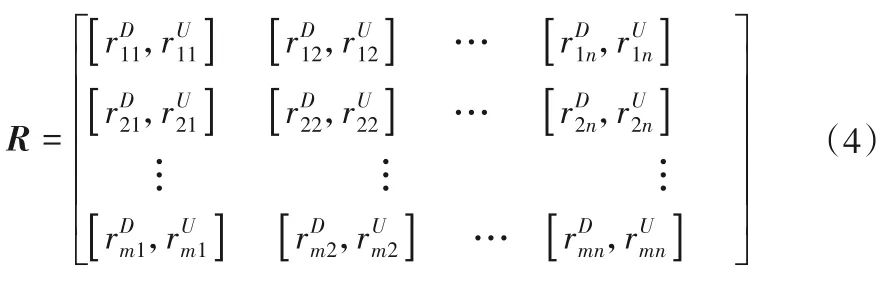
2 基于博弈組合賦權法的改進VIKOR模型

2.1 模型的權重確定方法

VIKOR 模型是一種折衷的多屬性決策方法，由Opricovic［19］最先提出，通過比較各方案與正負理想解的接近程度來對方案集進行排序，排序的基本思想是基于Lp-metric 聚合函數，見式（5）。較其他決策模型來說，VIKOR 模型增加了對決策結果進行可接受優勢度準則和可接受可靠性準則的驗證，這提高了決策結果的合理性與科學性。

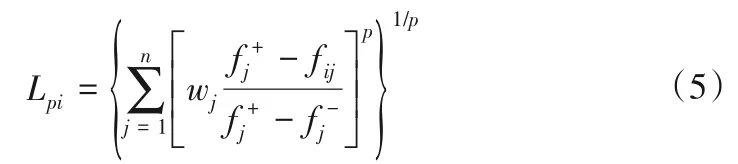
式中：fij為方案i中指標j的評價值；fj+為指標j的最優值；fj-為指標j的最劣值；wj為第j個指標的主觀權重值；p為距離參數，1 ≤p≤∞，通常取1、2或∞。

上述模型中權重的確定是指標值確定以后的關鍵，目前，確定權重的方法主要有2類：一是主觀賦權法，主要由決策者根據經驗主觀定權，其受主觀因素影響大；二是客觀賦權法，通過對統計數據所包含的客觀信息提取分析來確定權重，該方法完全依賴于客觀數據，忽視了評價指標自身的重要性，而且客觀數據中包含著噪聲信息，因此計算結果有可能不滿足要求。權重的恰當確定應該是評價指標客觀信息與評價者主觀判斷兩者綜合的反映。博弈論的組合賦權法是借鑒博弈論理論，將單一賦權方法看做是博弈中的局中人，以不同賦權方法的離差最小為博弈結果，對單一賦權方法進行賦權，并將其組合得到基于博弈論的組合賦權法［20］。其組合權重與主、客觀權重的偏差最小，提高了賦權的科學合理性［21］。

2.1.1 基于序關系分析法的主觀賦權法

主觀賦權法是根據專家自身的知識和經驗對各評價指標按照重要性進行排序和賦權，所得權重受主觀因素影響比較大。常用的方法有德爾菲法、專家排序法、層次分析法（AHP）、序關系分析法（GI），本文選取GI法［22，23］。

其主要計算步驟如下：

（1）按照各指標的重要性程度進行排序，若指標aj的重要程度小于指標a′j，則記為aj?a′j。按此準則對評價指標集A=(aj|1 ≤j≤n)進行排序，確定指標的序關系。

（2）由專家確定相鄰指標aj-1與aj間相對重要程度ESj，ESj的取值參考文獻［24］，ESj與相鄰指標aj-1、aj的關系如下式：

式中：wj-1、wj分別為第j-1和第j個指標的主觀權重值。

（3）按式（7）獲取各指標權重值。

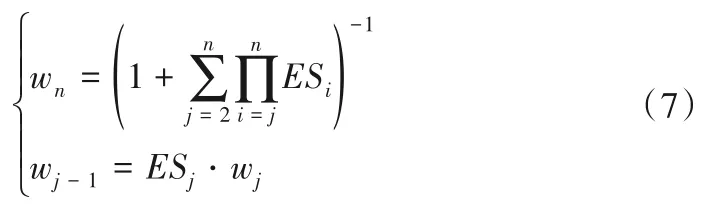
2.1.2 客觀權重因子的確定

對于客觀權重采用Critic 法［25］確定，Critic 法既能夠通過對比強度表示指標序列內部信息，又可以利用沖突性來挖掘指標間的相關關系，指標的重要性程度完全利用數據自身的客觀屬性進行科學評價，而不是由值的大小來決定。

第j個指標的信息量可以用下式表示：

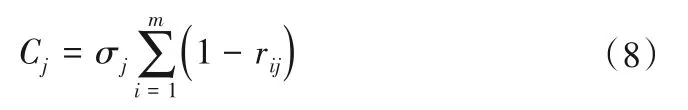
式中：σj為標準差，來表征不確定性信息的多少；Cj為信息量，值越大說明第j個評價指標在評價體系中的作用越大。

第j個指標的客觀權重值由下式得到：

式中：w′j為第j個指標的客觀權重值。

2.1.3 博弈論組合賦權的計算步驟

（1）基于GI 法和Critic 法分別得到主、客觀權重，權重向量集可以表示為wk={wk1，wk2，...，wkn}，k=1，2；則權重向量與權重系數α的線性組合為：

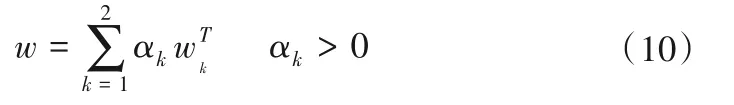
（2）借鑒博弈論的均衡思想［26］，通過式（11）對不同權重的線性組合進行優化，尋求主觀權重和客觀權重之間的一致。

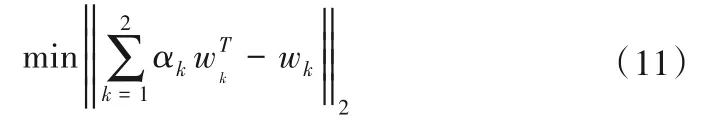
與式（11）等價的最優化一階導數線性方程組為：

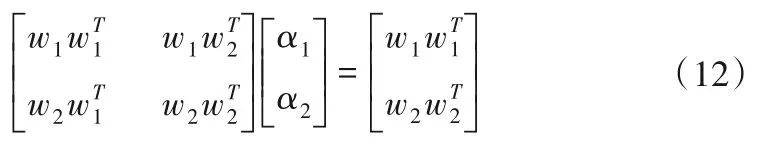
（3）由式（12）得到權重系數向量α1、α2，并對權重系數進行歸一化處理得到權重系數向量組α*。

（4）α*帶入權重向量矩陣w，則組合賦權的綜合權重w*為：

2.2 模型求解的具體步驟

（1）確定每個指標的正理想值（PIS）和負理想值（NIS），具體如下：

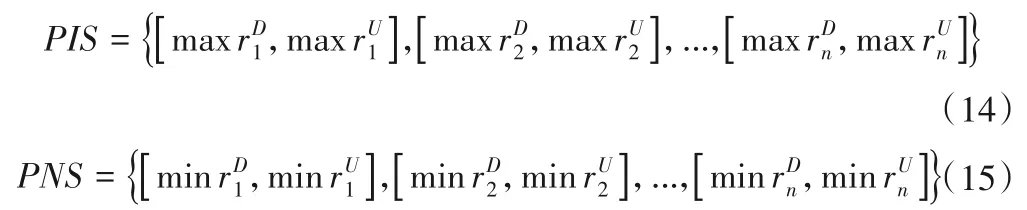
（2）確定群體效用值（Si）和個體遺憾值（Gi），具體如下：

（3）依據Si和Gi確定群體利益系數Qi，具體如下：

式中：β為折衷系數，取值范圍為［0，1］，其值的大小代表決策時群體效用和遺憾效用所占的比例，取值為0.5 時通過協商機制進行決策，故本文取0.5。

（4）根據各評價方案S、G、Q值的大小進行升序排序，值越小的表明評價對象越好。

（5）根據下面兩個條件選取妥協解，若最優決策方案同時滿足這兩個條件，則可以單獨根據Qi的值進行排序：

條件二：在各個方案中排序，依據S或者G值排在前面的方案。

3 算例分析

為了探究改進的VIKOR 模型在入庫徑流不確定下多目標優化調度方案決策中的應用，本文以三峽水庫為例，重點研究防洪、發電的多目標優化調度決策問題。參考文獻［27］，通過優化汛前過渡期的初始水位來使防洪和發電綜合效益最大。選取5月下旬到6月上旬為調度期，以日為計算時段。由于枯水年時一般防洪和發電的矛盾會更大一些，選取2006年實際和預報徑流資料進行分析，評價指標有發電量、防洪效益和防洪指標超越風險率［28］。通過對考慮模擬預報誤差得到的1 000 場徑流過程進行多目標優化調度，得到的各評價指標值見表1。

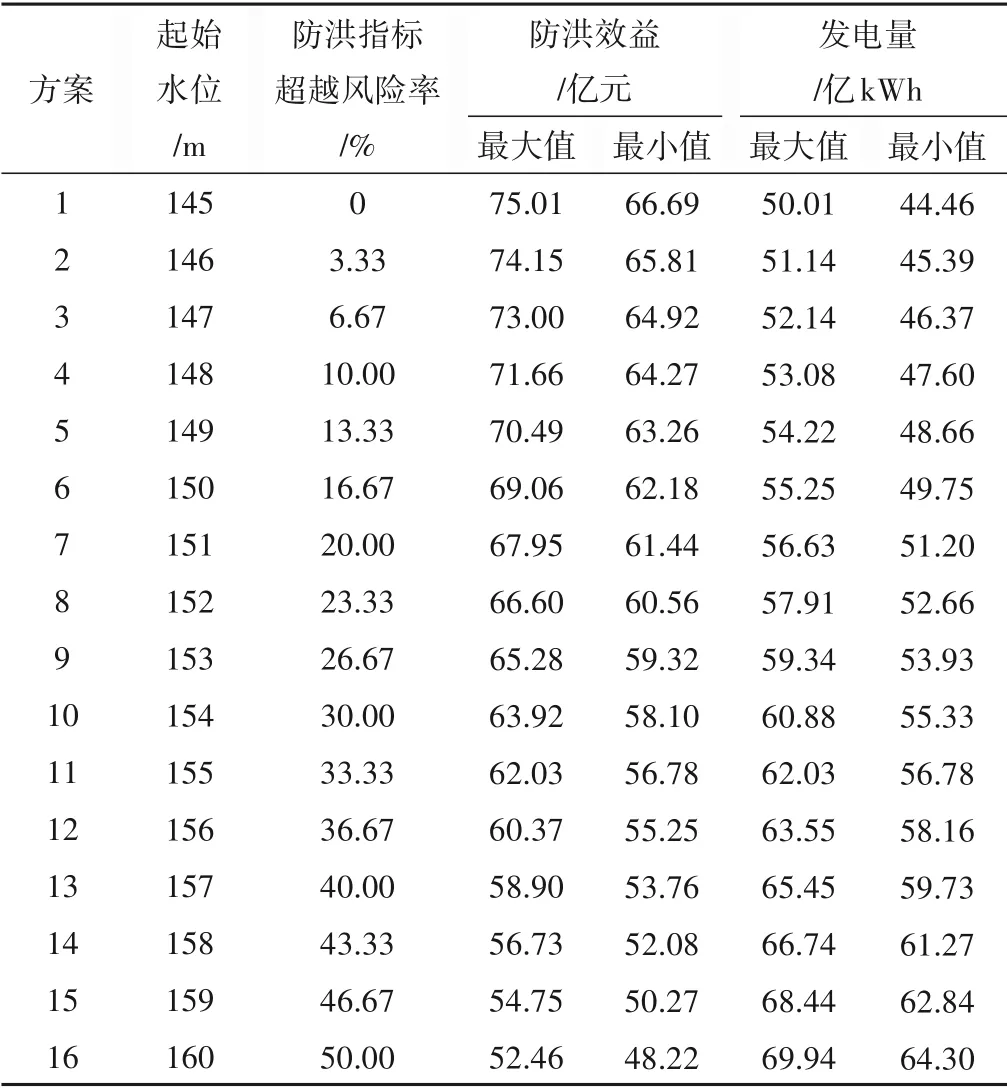
表1 模擬徑流過程的各評價指標值Tab.1 The evaluation index values of simulated runoff process

（1）對表1的指標集進行標準化處理，得到決策矩陣R：

（2）主觀權重的確定。

①指標的重要程度排序為P防洪＞F防洪＞E發電；防洪指標超越風險率比防洪效益稍微重要，防洪效益比發電量明顯重要。

②根據ESj取值表，專家選取ES2=1.1；ES3=1.4。

③利用式（7）得到防洪指標超越風險率、防洪效益和發電量的主觀權重為：

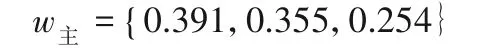
（3）客觀權重的確定。根據Critic 法，依據式（8）和式（9）計算得到防洪指標超越風險率、防洪效益和發電量的客觀權重為：

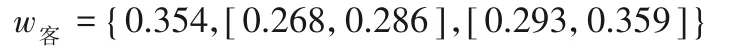
（4）綜合權重的確定。根據博弈論法，依據式（10）到（13）可得綜合權重為：

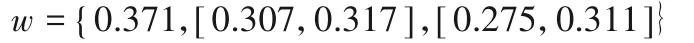
（5）依據式（14）和（15）確定正負理想值。

（6）采用式（16）到（18）對模型評價參數S、Q、G進行計算，值取區間值的平均數；并根據S、Q、G的均值對各方案進行排序，各方案的參數值及排序結果見表2。

表2 模型評價參數值及方案排序Tab.2 Model evaluation parameter value and scheme ranking

實際徑流過程最優方案的選取：選取Q排序第一的方案8，依據G排序仍排在第1，滿足條件二；m=16，1/（m-1）=1/15=0.067，按照指標Q排在第二的是方案7，Q7-Q8=0.040＜0.067，也滿足條件一。故選取方案8為最優方案。

模擬徑流過程最優方案的選取：選取Q排序第一的方案8，依據G排序仍排在第1，滿足條件二；按照指標Q排在第二的是方案Q7-Q8=0.028＜0.067，也滿足條件一。故選取方案8 為最優方案。

結果的合理性分析：①按照群體效用值S排序第一的為方案1，從而可以看出對S值來說偏重于防洪效益和防洪指標超越風險率。方案8 的S值排序為第八，Q值和G值都排第一，綜合效益相對最優。②方案8的調度期初始水位為152 m，防洪指標超越風險率為23.33%，防洪效益均值為63.58億元，發電量均值為55.29 億kWh；雖然方案8 的發電量不是所有方案中最大的，但其是在保證水庫安全的基礎上，增加了水庫的發電效益，綜合效益相對來說比較優。若調度期初始水位低于152 m 的話，本可以在不影響水庫防洪安全的基礎上繼續抬高初始水位，而增加發電效益；卻仍舊保持在低的初始水位，浪費了水量。若在152 m 的基礎上繼續抬高初始水位的話，雖然增加了發電效益，但是此時犧牲防洪效益而換來的發電效益是不對等的，防洪指標超越風險率較大。③模擬徑流過程所選的最優方案和實際徑流過程所選方案一致，說明按照區間數來處理不確定性來流情況下的多目標決策方法可行且有效，可為實際水庫多目標運行調度提供理論和技術支撐。

4 結 論

本文在考慮入庫徑流不確定的基礎上，基于區間數理論、博弈論綜合賦權法對VIKOR模型進行了改進，并應用于三峽水庫入庫徑流不確定下水庫多目標優化調度方案的決策，并與實際入庫徑流情形下的結果進行對比分析。得到主要的結論如下。

（1）用區間數來表征入庫徑流預報誤差的不確定性，兼顧了多種來水情況下的調度結果，其多目標優選方案與實際來水情況下的優選方案基本一致，為入庫徑流不確定下水庫多目標優化調度決策提供了一種新思路。

（2）在考慮主觀意愿和客觀事實的基礎上，博弈論綜合賦權法極小化了主客觀權重之間的偏差，與區間數和VIKOR模型的綜合運用，提高了決策過程和決策結果的合理性和可信度，對于水庫多目標調度決策是一次有意義的嘗試。

（3）需要說明的是本文對VIKOR 模型的改進思路同樣可以應用于模糊方法、AHP 方法等多目標評價方法，從而對入庫徑流不確定下水庫多目標優化調度方案的決策方法進行豐富和完善，這些方法的優勢對比分析是下一步的重點研究方向。 □