ECOC多分類算法在慕課數據挖掘中的應用

潘麗芳，謝書童，曹秀娟

(1.集美大學理學院，福建 廈門 361021；2.集美大學計算機工程學院，福建 廈門 361021)

0 引言

近年來，隨著慕課在線學習課程迅速普及，更多的學生得到了便捷高效的學習體驗[1]。然而，慕課動則成千上萬名學生在一起大規模的學習模式，與現代教育理念中學生學習的個性化需求形成了尖銳的矛盾。在慕課規模化教學條件下，合理引導并實現學生的個性化學習是一個教育和學術并重的問題，具有重要研究價值[2-3]。

蔣卓軒等[4]對北京大學在Coursera平臺上開設的6門慕課的學習行為數據進行分析與挖掘。結果表明，基于學習行為特征的數據分析能有效地判別一個學生最后能否獲得課程證書。Qiu等[5]基于清華大學學堂在線的慕課數據，提出用潛在動態因子圖模型(latent dynamic factor graph，LadFG)來預測學生作業情況，以及能否通過考試獲得證書。Xu等[6]通過分析學生在慕課平臺上的活動日志，歸納出不同學生的學習動機，設計出基于支持向量機(SVM)的分類算法預測學生能否取得證書。Zhang等[7]對北大《數據結構與算法》與《計算機導論》兩門慕課，匯聚多源異構數據，分析學生的學習內容，識別課程中的重要概念，通過學生測驗數據來評估學生的知識狀態，并設計出算法預測學生是否中途退課。Yu等[8]根據學生的視頻點擊流日志，識別出學生的七種認知參與模型，設計了基于K最近鄰(KNN)、SVM、人工神經網絡(ANN)的分類算法，預測學生能否通過課程考試。

為了提高傳統線下課程與線上慕課的教學效率，Meier等[9]利用課程的歷史教學數據(主要包括作業、小測、期中考試等)，預測學生在后繼學習中的可能表現(好/差)，為提前對學習不佳的學生進行教學干預贏得時間。Xu等[10]設計了一個雙層結構的集成分類系統，對學生不斷變化的學習狀態進行動態預測，并提出了一種基于潛在因子模型和概率矩陣分解的數據驅動方法，發現了課程的相關性，從而提高預測準確度。Ulloa-Cazarez等[11]提出遺傳規劃(genetic programming，GP)算法預測學生能否通過期末考試。為了識別出學習《數字設計》課程有困難的學生，Hussain等[12]使用ANN與SVM等算法，利用學習系統上的學習行為數據，預測出學習困難的學生，方便提前教學干預。

上述研究工作大多根據慕課中的學習行為數據，設計分類預測算法來預測后續學習成效，即預測學生能否通過考試、提前退課、順利畢業等，這實質上是一個二分類問題的研究。然而，學生學習成效的多分類預測比二分類更有利于學生個性化教學的實施，但多分類預測難度較大，目前國內外有關慕課數據的多分類預測的研究很少。本文提出基于數據復雜度的糾錯輸出編碼(error correct output codes，ECOC)多分類算法，對慕課數據進行挖掘，以期實現對學生成績的多分類預測，即預測學生成績的四個等級(優、良、合格、不合格)，為個性化和差異化的教學干預提供理論基礎與技術條件。

1 基于數據復雜度的ECOC分類算法

本文提出的基于數據復雜度的ECOC分類算法，首先利用數據復雜度降低兩個分類的復雜度，然后，利用ECOC算法實現多個二分類預測，從而實現多分類預測。該算法主要分為二個步驟：基于數據復雜度的二分類調整方法;基于ECOC的多分類預測。

1.1 基于數據復雜度的調整方法

數據復雜度是通過分析數據特征來衡量數據樣本分類的難易程度[13-14]。數據復雜度越高的分類問題，算法越難以實現正確的分類預測。因此，本文采用了多種數據復雜度方法降低二分類問題的分類復雜程度，它們分別是費希爾判別率(F1)、交叉重疊體積(F2)、重疊區域數據點數(F3)、同類實例與異類實例距離比(N2)、基于最近鄰分類器的錯誤率(N3)、INN分類器的誤差率(N4)、非線性分類器的非線性特點(L3)，以及基于質心匹配的方法(C1)[13]。

1.2 ECOC多分類算法

ECOC多分類算法最早由通信領域為解決信號傳輸問題而提出，其處理問題的關鍵在于選擇高效優秀的編碼策略和解碼策略[15]。ECOC多分類算法的主要策略是將多類問題轉化為多個二分類問題進行求解。ECOC多分類算法包括三個基本步驟：編碼、訓練、解碼。

編碼策略的設計是為了得到實現多類分解和基分類器集成的編碼矩陣。編碼矩陣是由二元(-1，+1)或者三元(-1，+1，0)組成，其中-1代表負類，0代表對應的類在分類時被忽略，+1代表正類；行向量表示一個類別，列向量表示一個基二分類器。此外，編碼策略分數據無關和數據相關兩種類型。數據無關主要是指編碼時不依賴數據樣本，數據相關是指編碼時樣本特征的分布緊密聯系著編碼矩陣。數據無關算法包括一對一(One Vs.One, OVO)、一對多(One Vs.All,OVA)、稀疏隨機(sparse random)和密集隨機(dense random)策略。數據相關算法包括DECOC、Forest-ECOC、ECOC-ONE等。編碼矩陣行列應盡可能不同，減少基二分類器和碼字之間的相關性。訓練步驟就是通過訓練數據對ECOC及其相應的基分類器進行訓練，從而調整ECOC及其基分類器的參數。

解碼策略是指在測試某個樣本時，每個基二分類器都會產生一個相同長度的向量作為輸出，然后計算出輸出向量與編碼矩陣中的碼字之間的距離，選擇距離最小的碼字作為最終結果，并將相應的類別標簽賦予該樣本。解碼策略包括AED、ED、ELB、ELW、HD、LAP、LLB等。

1.3 算法框架

首先，基于數據復雜度的ECOC分類算法需將所有的類別隨機分成數量盡可能相同的兩組，然后對每個類別進行相同的數據復雜度評估，再交換兩個組中具有最高復雜度的兩個類，從而降低兩個組組內整體的數據復雜度，提高對應基二分類器的泛化能力。通過降低類別之間的數據復雜度，使得分類算法更容易區分不同類別，從而達到提高預測準確率的目標。在追求降低組內整體復雜度時，F1和F3兩種數據復雜度評價指標是相反的，應盡可能提高組內F1或F3指標的值才能降低復雜性。不斷調整以上類別分組過程以達到最優分配，即組內數據復雜度達到最低，形成類別樹形分布。將節點編碼為+1或-1(沒有參與分類的節點編碼為0)，形成編碼矩陣的一列，得到編碼矩陣后，再用訓練分類器對樣本進行預測，算法整體框架如圖1所示。

2 實驗結果與分析

2.1 數據集與實驗參數設置

收集并整合三所高校的計算機基礎課程的慕課數據，預處理后的類別數量、特征數量、樣本數量如表1所示。根據學生的期末成績，把學生樣本劃分成四類:分數位于0(含0)到60之間判為第4類，分數位于60(含60)到75之間判為第3類，分數位于75(含75)到85之間判為第2類，分數位于85(含85)到100(含)之間判為第1類，亦即為不合格、合格、良與優四個等級。該課程的知識點包括硬件系統組成、操作系統與常用軟件、音頻和圖像處理、數據庫技術、算法、無線通信技術、加密解密算法，以及網絡安全等。將相應的知識點做成教學視頻放于慕課平臺供學生學習，且每章均有課后習題，另有階段性小測，以鞏固學生對知識點的掌握。本研究收集了學生在慕課平臺觀看教學視頻的行為數據(包括訪問時間、訪問時長、所用電子設備)、教學視頻中的答題數據、章節作業數據、小測數據，以及線下期末成績等大量細粒度的學習行為數據。

表1 學生慕課學習行為數據集

算法在Matlab上實現，并調用Sklearn工具包。為充分驗證算法的有效性，實驗均采用十折交叉法進行測試，取平均值作為評價標準；均采用了兩種基二分類器，即SVM和樸素貝葉斯(NB)；所有算法的解碼策略均采用ELW(即指數損失加權解碼)方式。五種傳統ECOC算法，即編碼策略為OVO、OVA、DECOC、ECOC-ONE、Forest-ECOC的均進行了相應的實驗，以對比本文提出的基于數據復雜度的ECOC與傳統ECOC的算法性能。

2.2 實驗結果分析

如表2和表3所示，準確率最高的實驗結果采用下劃線并加粗標識。從表2基于SVM的ECOC算法的預測結果可以發現：在學校A數據集上，基于數據復雜度的ECOC算法和其他ECOC算法性能相近，準確率在81%左右；在學校B數據集上，基于質心匹配的數據復雜度C1的ECOC算法預測準確率最高，達到73.32%，與基于數據復雜度的ECOC算法性能相近，但比傳統ECOC算法準確率平均提升約0.6%；在學校C數據集上，基于質心匹配的數據復雜度C1的ECOC算法獲得最高準確率，可達73.55%，基于數據復雜度的ECOC算法相比其他ECOC算法準確率平均提升約0.51%；在所有編碼方式中，基于質心匹配的數據復雜度C1的ECOC算法獲得最優平均準確率為75.95%。綜上分析可得，基于數據復雜度的ECOC算法相比于傳統ECOC算法具有更優的性能。

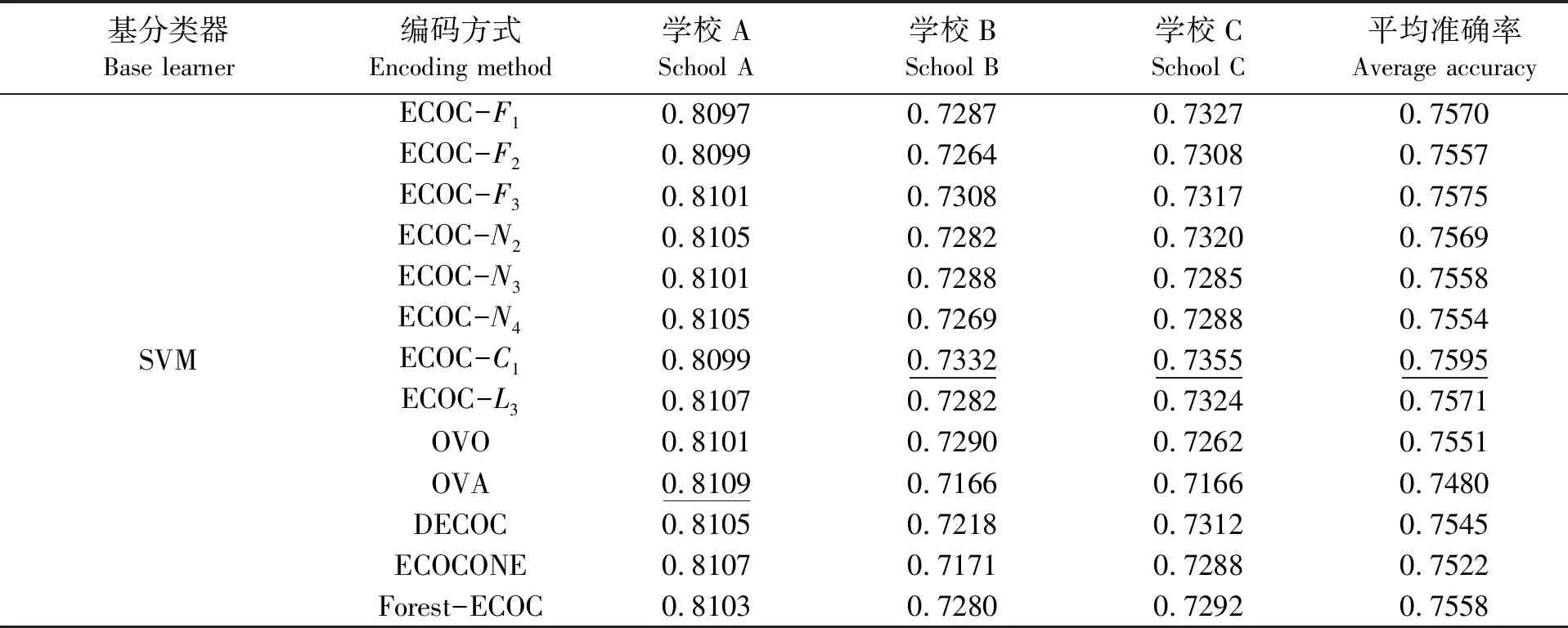
表2 基于SVM的不同ECOC算法的準確率對比

基于NB的ECOC算法的結果如表3所示。在所有算法中，基于最近鄰分類器的錯誤率數據復雜度N3的ECOC算法在三個數據集上平均分類準確率最高，達到68.95%。在學校A數據集上，OVA算法取得最好的準確率，即71.56%，其余ECOC算法的準確率相近；在學校B數據集上，DECOC算法取得最好的準確率，即70.26%；在學校C數據集上，基于最近鄰分類器的錯誤率數據復雜度N3的ECOC算法取得最好的準確率，即67.63%。從平均準確率上看，基于數據復雜度的ECOC算法和傳統ECOC算法并沒有明顯的差距。

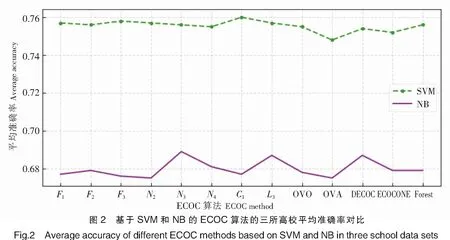
由表2和表3的結果可得，在學校A、B、C三個數據集上，基于SVM的ECOC算法的性能明顯優于基于NB的ECOC算法，平均預測準確率分別提高了約11%、4%、6%。由圖2可以看出，基于SVM的ECOC算法預測的平均準確率(三個數據集的準確率平均值)明顯優于基于NB的ECOC算法。進一步可以發現，在采用SVM為基分類器情況下，ECOC算法結果總體波動較小，其中基于數據復雜度的ECOC算法性能更加穩定，且優于傳統ECOC。相反地，在基于NB分類器情況下，ECOC算法準確率波動較大，其中基于數據復雜度的ECOC算法效果較好。

表3 基于NB的不同ECOC算法的準確率對比

3 結論

本文收集并整合三個高校學生的慕課學習行為數據，設計了包括多種基于數據復雜度的ECOC算法，并與傳統ECOC算法在內的十多種基于ECOC的多分類算法進行比較。實驗結果表明，相比于傳統的ECOC算法，基于數據復雜度的ECOC多分類算法預測精度更高、更穩健，其對學生成績進行四個等級的預測，平均準確率可達75%以上，為提前教學干預提供了參考。

未來可考慮用更多的數據復雜度算法來計算三所高校數據的復雜度，衡量數據內部分布情況。此外，算法中基分類器的多樣性影響著ECOC算法的性能，因此，豐富基分類器的多樣性也是值得深入研究的方向。