隨機單種群Gompertz增長模型的穩定性

王鳳筵

(集美大學理學院,福建 廈門 361021)

0 引言

單種群增長的Logistic模型、Gompertz模型是生物數學和經濟學中的兩個重要的數學模型。種群的生存環境總是受到各種隨機不確定因素的影響，因此,很多學者研究了隨機Logistic模型[1-9]：dx(t)=rx(t)(1-x(t)/K)dt+σx(t)dBt，其中，x(t)表示t時刻的種群密度，r>0表示種群內稟增長率，K>0表示種群的環境容納量，σ表示白噪聲強度，Bt是標準布朗運動。文獻[2]研究了非自治的隨機Logistic方程的依時間平均的持久性和滅絕性；文獻[4]研究了非自治的隨機Logistic方程的依時間平均的全局穩定性、持久性和滅絕性；文獻[5]研究了基于隨機Logistic方程建立的捕食-食餌的分支問題；文獻[6]研究了帶有脈沖擾動的非自治的隨機Logistic方程的依時間平均的持久性、滅絕性、全局吸引性和隨機持久性。但是,當用依時間平均的概念研究隨機單種群增長的Gompertz模型時,就遇到無法克服的困難。因此,研究Gompertz模型穩定性甚至何種意義下的穩定性,可以參考的文獻很少。

本文引入依均值平方吸引和隨機有界性概念，研究下面的隨機單種群增長的Gompertz模型[9]:

dx(t)=rx(t)(μ-lnx(t))dt+σx(t)dBt,

(1)

其中：eμ表示種群的環境容納量;σ表示白噪聲強度;Bt是標準布朗運動。關于模型(1)的研究結果是比較少的，而關于確定性單種群Gompertz模型

dx(t)=rx(t)(μ-lnx(t))dt

(2)

的研究是很多的。方程(2)所描述的種群數量x(t)漸進穩定到環境容納量,種群沒有滅絕平衡態。本文引入依均值吸引和依均值平方吸引的概念，研究了隨機Gompertz方程漸進的行為。

1 預備知識和隨機全局正解

定理1[9](It公式)設x(t)(t≥0)是It過程,其隨機微分為dx(t)=f(t)dt+g(t)dBt，其中：f∈L1(R+,Rn);g∈L2(R+,Rn×m)。若V(x(t),t)∈C2,1(Rn×R+;R),則V(x(t),t)仍然是It過程,具有如下隨機微分：dV(x(t),t)=Vt(x(t),t)dt+Vx(x(t),t)dx(t)+0.5dxT(t)Vxx(x(t),t)dx(t)。

定理2 對任意給定的初值x(0)=x0>0,系統(1)存在唯一全局正解x(t)，并且有如下表達式：

(3)

證明在方程dx(t)=rx(t)(μ-lnx(t))dt+σx(t)dBt作代換u(t)=lnx(t)。應用It公式可得：

du(t)=d lnx(t)=dx(t)/x(t)-(dx(t))2/(2x2(t))=

(rμ-σ2/2-rlnx(t))dt+σdBt=(rμ-σ2/2-ru(t))dt+σdBt。

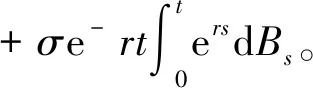
為了研究隨機解的均值,需要下列引理1。

(4)

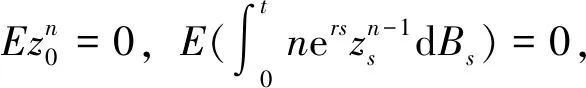
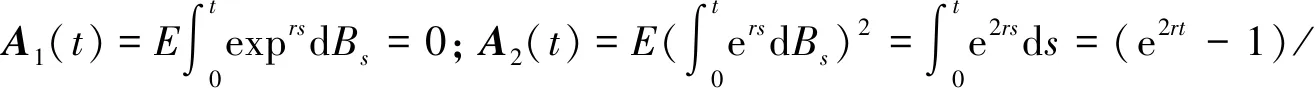
應用上面的結果,經過如下運算可以得到：

(5)

證畢。

應用引理1和定理2可得定理3。

定理3 對任意給定的初值x(0)=x0>0,系統(1)有正解x(t)，Ex(t)和Ex2(t)，并有如下表達式：

Ex(t)=exp{e-rtlnx0+(μ-σ2/(2r))(1-e-rt)+σ2(1-e-2rt)/(4r)}，

Ex2(t)=exp{2e-rtlnx0+2(μ-σ2/(2r))(1-e-rt) +σ2(1-e-2rt)/r}。

2 依均值平方的穩定性和隨機最終有界性

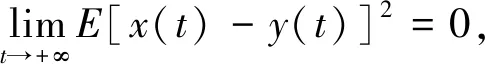
定理4 方程(1) 是依均值的平方全局吸引的，且對于任意給定系統(1) 的兩個解x(t),y(t)對應的初值為x(0)=x0>0,y(0)=y0>0,有如下的估計：

E[x(t)-y(t)]2=[lnx0-lny0]2exp{2(μ-σ2/(2r))+σ2/r)}e-2rt+o(e-2rt),t→+∞。

證明任意給定系統(1)的兩個解x(t)，y(t)對應的初值為x(0)=x0>0,y(0)=y0>0,那么,由表達式

E[x(t)-y(t)]2=[exp{e-rtlnx0}-exp{e-rtlny0}]2exp{2(μ-σ2/(2r))(1-e-rt)+σ2(1-e-2rt)/r}

可以得到定理4的結論。

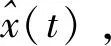
定理5 方程(1)的解x*(t)是依均值的平方全局吸引的,其中,x*(t)表達如下：

隨機解x*(t)有以下的性質：

Ex*(t)=exp{e-rt(μ-σ2/(4r))+(μ-σ2/(2r))(1-e-rt)+σ2(1-e-2rt)/(4r)},

Varx*(t)=exp{2e-rt(μ-σ2/(4r))+2(μ-σ2/(2r))(1-e-rt)}

{exp{σ2(1-e-2rt)/r}-exp{σ2(1-e-2rt)/(2r)}}。

證明任意給定系統(1)的兩個解x(t)，y(t)對應的初值為x(0)=x0> 0,y(0)=y0>0,那么,經過運算可得：

E|x(t)-y(t)|=|exp{ertlnx0}-exp{e-rtlny0}|exp{(μ-σ2/(2r))(1-e-rt)+

σ2(1-e-2rt)/(4r)}=|lnx0-lny0|exp{μ-σ2/(4r)}e-rt+o(e-rt),t→+∞。

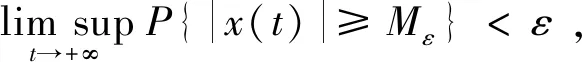
定理6 方程(1)是隨機最終有界的。