一類中立型Cohen-Grossberg神經網絡的概周期解

方聰娜

(集美大學理學院，福建 廈門 361021)

0 引言

Cohen-Grossberg神經網絡在模式識別、并行計算、優化、信號和圖像處理等不同領域都有廣泛的應用，許多學者研究了各種具有時滯的Cohen-Grossberg神經網絡的平衡點、周期解、概周期解的存在性、唯一性、穩定性等，并取得了一些很好的研究成果[1-4]。但是，由于神經細胞在現實世界中具有復雜的動態特性，為了更準確反映神經元反應過程的特性，有必要在神經系統的數學模型中加入一些關于過去狀態的導數的信息，這種新型的神經網絡被稱為中立型神經網絡。近年來，一些學者主要利用Lyapunov泛函、線性矩陣不等式、積分不等式、重合度理論、M矩陣等方法，研究了各種中立型Cohen-Grossberg神經網絡的動力學行為，并得到了一些新的結論[5-6]。然而，從現有文獻來看，對于具有時滯的中立型Cohen-Grossberg神經網絡的概周期解的相關問題的研究還是比較少。基于此，本文研究如下一類具有混合時滯的中立型Cohen-Grossberg神經網絡

(1)

的概周期解。其中：xi(t)表示第i個神經元在t時刻的狀態；αi(t,·)表示放大函數；βi(t,·)表示行為函數；aij(t),bij(t),cij(t)表示神經元之間的連接權重；fj(·),gj(·),hj(·)表示神經元激活函數；τij(t)表示傳輸時滯且滿足0≤τij(t)≤τ(τ>0為常數)；kij(s)表示分布時滯核函數；Ii(t)表示第i個神經元在t時刻的外部輸入。本文通過建立線性輔助方程的技巧，得到了系統(1)存在唯一的概周期解的新結果，同時也給出了此概周期解的存在范圍。

1 主要結果

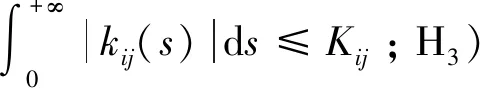
2 定理1的證明

對任意的φ(t)∈Ω，由條件H1)、H2)可構造如下線性概周期微分系統

(2)

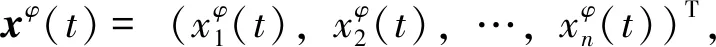
(3)

因為xφ(t)∈Ω, 所以可定義映射Φ:Ω*→Ω為Φ(φ)=xφ。 對任意的φ∈Ω*,下面證明xφ(t)∈Ω*。

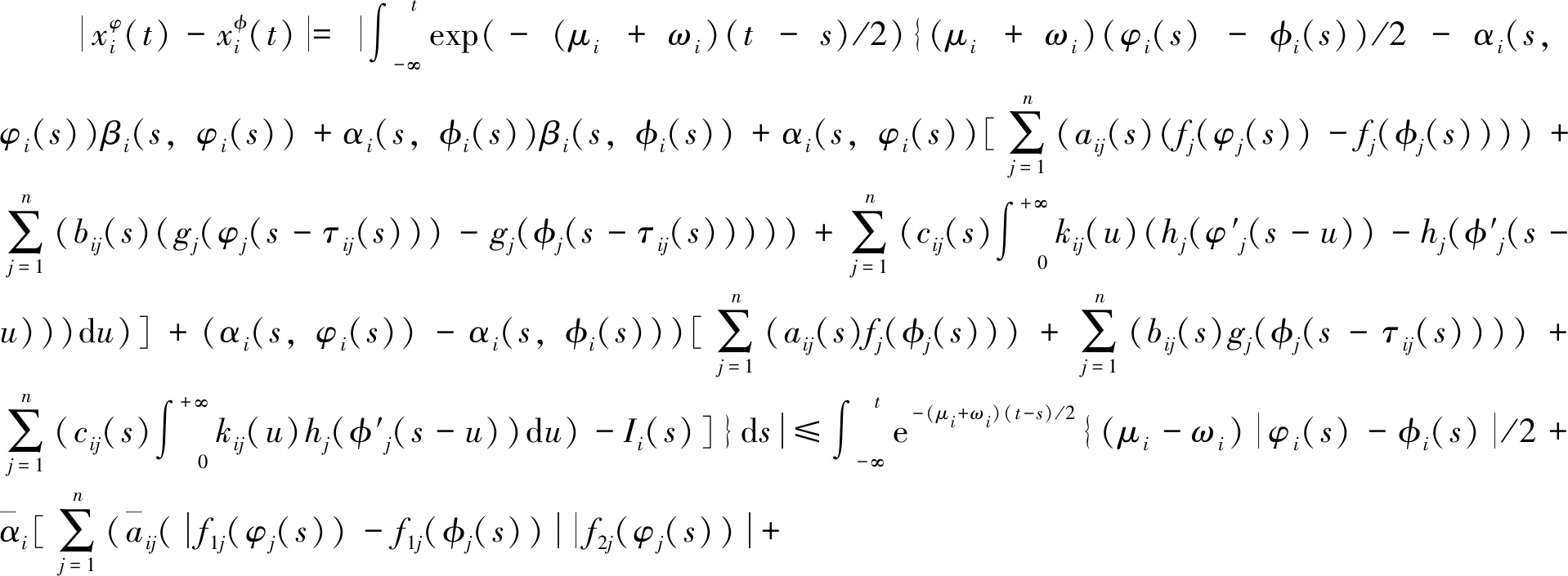
注1 文中的方法可以用來研究一些其他具有時滯的Cohen-Grossberg神經網絡的概周期解問題。