Riesz空間分布階的分數階擴散方程的數值模擬

陳景華，陳雪娟

(1.集美大學理學院，福建 廈門 361021；2.集美大學理學院數字福建大數據建模與智能計算研究所，福建 廈門 361021)

0 引言

分數階微分方程是廣義的非整數階的微分方程。由于分數階算子的非局部性，分數階微分方程非常適合用來描述現實世界中具有記憶及遺傳性質的材料[1-3]。 然而，還有很多問題不能采用分數階系統來解決，如非均質多孔和裂隙介質中的溶質遷移試驗[4-5]。由于復雜流體流動的力學性質會隨時空尺度而發生一定的變化，因此污染物等溶質擴散將產生所謂的多尺度效應。 近年來，研究者們[6-9]采用Riesz分布階的分數階擴散方程(其中分布階導數在數學上可以看成是對分數階導數在給定范圍內關于其階數的一個積分，即分數階導數是在一個單位區間上的積分)來描述這種反常擴散。Diethelm等[10]研究了Caputo分布階常微分方程的數值解并進行了收斂性分析；Atanackovic等[11]證明了時間分布階柯西問題解存在性，并求出解析解；Luchko等[12]考慮了一個開區間上的分布階時間分數階擴散方程，并證明了這個問題的解的唯一性和存在性；Jiao等[9]給出了分布階導數在信號處理中的分布階的濾波器和控制系統中的最優分布階阻尼兩個應用。 Podlubny等[13]用矩陣方法離散分布階導數和積分,給出數值例子驗證算法的精確性，但是沒有具體的數值理論分析；Gorenflo等[14]研究了一種分布階時間分數階擴散波動方程，并利用傅里葉變換和拉普拉斯變換技術得到了此問題的基本解。現有文獻關于分布階微分方程數值方法的研究還比較少。2014年，Katsikadelis[15]研究了Caputo分布階線性與非線性常微分方程的數值解，但沒有進行理論分析。2018年，Semarya等[16]運用移位的分數階積分切比雪夫算子矩陣與修正的Picard數值方法求解分布階線性分數階常微分方程，但沒有進行理論分析。分布階微分算子作為分數階微分算子的發展形式，已經越來越受到研究人員的重視。相對于固定階導數，這類算子的應用領域更為廣闊，但由于算子定義的復雜性，相應的數值算法更為復雜，并不能簡單照搬分數階的數值算法。本文考慮用有效的數值方法求解空間分布階的分數階擴散方程。

考慮以下Riesz空間分布階的分數階擴散方程[17-18]：

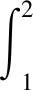
(1)

邊界條件：

u(xL,t)=0,u(xR,t)=0,t∈(0,T],

(2)

初始條件：

u(x,0)=φ(x),x∈[xL,xR],

(3)

這里P(α)是非負加權函數[10]，滿足：

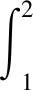
(4)

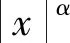
(5)

這里cα=-1/(2cos(πα/2)),且

(7)

1 積分項的離散

首先，把積分區間劃分成若干個子區間：1=α0<α1<…<αS=2,S∈N，并記

Δαi=αi-αi-1=1/S=σ,αi-1/2=(αi-1+αi)/2,i=1,2,…,S。

(8)

(9)

(10)

則Riesz空間分布階的分數階擴散方程可以離散成具有多項分數階導數的微分方程：

?u(x,t)/?t=Dxu+f(x,t)+O(σ4)

(11)

具有邊界和初始條件(2)～(3)。

2 數值離散格式

首先對空間和時間進行離散。取正整數N,設時間步長τ=T/N,tn=nτ,0≤n≤N。記時間區域Ωτ={tn|0≤n≤N}。取正整數M，并設空間步長h=(xR-xL)/M,xi=xL+ih,0≤i≤M。空間區域Ωh={xi|0≤i≤M}。空間平均差分算子Aα定義為：

平均算子A定義為：

(12)

(13)

(14)

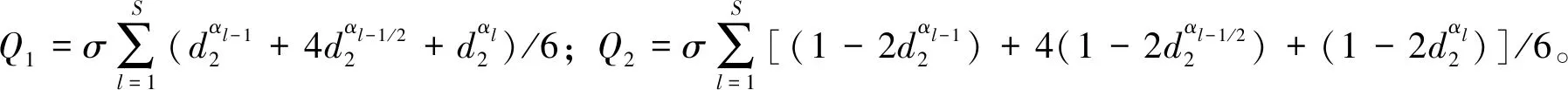
(15)

(16)

其中,

(17)

(18)

且

(19)

(20)

及差分算子δxu：

(21)

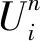
(22)

其中,

(23)

由方程(9)～(16)得到：

A(Dxu(xi,t))=δxu(xi,t)+O(h4)。

(24)

考慮方程(1)在點(xi,t)處的方程為：

ut(xi,t)=Dxu(xi,t)+f(xi,t)+O(σ4),

(25)

在方程(25)兩端取平均算子A，則有：

Aut(xi,t)=ADxu(xi,t)+Af(xi,t)+O(σ4),xi∈Ωh。

(26)

由式(24)可得：

Aut(xi,t)=δxu(xi,t)+Af(xi,t)+O(σ4+h4),xi∈Ωh。

(27)

下面對時間離散。對于方程(27)，在t=tn和t=tn+1處取平均，且利用泰勒展開，可得到：

(28)

(29)

(30)

得到以下四階擬緊差分格式：

(31)

(32)

為了逼近Riesz空間分布階的分數階擴散方程，將方程(31)改成：

(33)

線性系統(33)的系數矩陣A=(as,t)寫成下式：

(34)

則有以下的定理1。

定理1 差分格式(31)～(32)是唯一可解的。

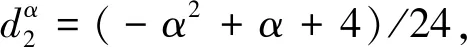
3 穩定性和收斂性的證明

為了證明差分格式的穩定性和收斂性，有以下引理。

引理1A是自相似的，即對任意的u,v∈Vh,成立(Au,v)=(u,Av)。

證明

(35)

即證得。

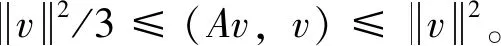
證明

(36)

且

(37)

可得

(38)

即證得。

引理3 對任意的v∈Vh, 成立(δxv,v)≤0。

證明

(39)

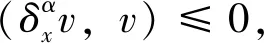
使用引理3，容易得到以下定理2，其證明類似文獻[18]的定理2。

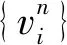
(40)

(41)

則有

(42)

由定理2可以直接推出如下定理3。

定理3 差分格式(31)～(32)按初值和右端項f是無條件穩定的。

現在考慮差分格式 (31)～(32)的收斂性。

定理4 差分格式(31)～(32)是收斂的，且收斂階為O(τ2+σ4+h4)。

(43)

將式(28)和式(29)分別減去式(31)和式(32)，可得到誤差方程

(44)

(45)

根據定理2得到：

(46)

證畢。

4 數值例子

例1 考慮以下Riesz空間分布階擴散方程：

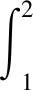
(47)

邊界條件：

u(0,t)=0,u(1,t)=0,t∈(0,1],

(48)

初始條件：

u(x,0)=x4(1-x)4,x∈[0,1]。

(49)

這里，

P(α)=-2Γ(9-α)cos(πα/2)，

(50)

且

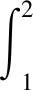
(51)

方程(47)～(49)的精確解為u(x,t)=e-tx4(1-x)4。

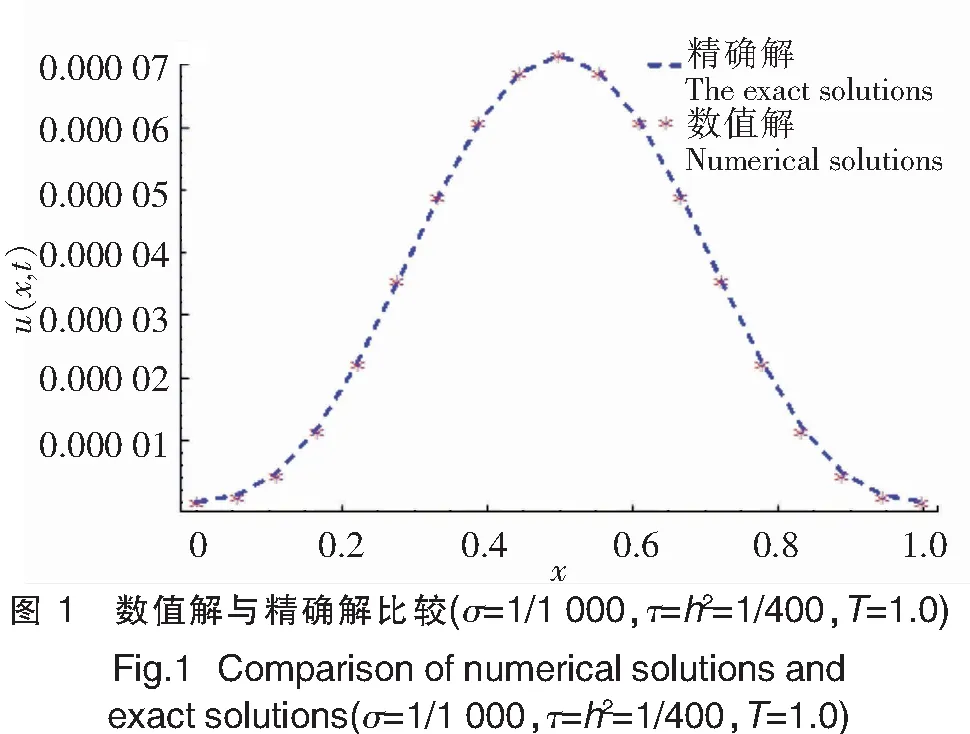
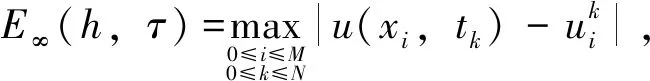
圖1顯示了T=1.0時刻數值解與精確解的比較,取σ=1/1 000、τ=h2=1/400二者非常吻合。表 1 顯示σ=1/1 000、τ=h2、T=1.0時數值解與精確解的最大誤差及收斂。誤差率接近:Rε=lg(ε(h1)/ε(h2))/lg 2≈4，這與定理4中差分格式的收斂階是O(τ2+σ4+h4)是一致的。從圖1和表1可以看出，數值結果與理論分析結果是一致的。

表1 T=1.0時刻數值方法的最大誤差和收斂階(σ=1/1 000，τ=h2)

5 結論

本文發展了一個Riesz空間分布階的分數階擴散方程的數值方法。將分布階方程離散為含有多項分數階導數的微分方程，利用有限差分法對得到的微分方程進行數值求解。證明差分格式是穩定的和無條件收斂的。此外，本文的數值方法的收斂階為O(τ2+σ4+h4)。最后，給出了數值例子來證明本文數值方法與理論結果是一致的。這種方法和分析技術可用于求解和分析其他類型的分數階偏微分方程。