基于邊界元法的壓裂液返排數值模擬

魏子俊， 程 萬， 蔣國盛， 周治東

(中國地質大學(武漢)工程學院， 武漢 430074)

中國非常規能源儲量極其豐富，有關資料表明，僅可開采頁巖氣中國約為25萬億 m3，和目前常規天然氣可采資源潛力相當，基本證實與美國等同為頁巖氣資源大國[1]，大力發展非常規油氣資源已成為“十三五”規劃以來中國油氣行業必然的戰略選擇[2]。在頁巖油氣等非常規能源開采中，油氣井產能效率在很大程度上取決于返排后裂縫的導流能力[3-5]。壓裂液若不能及時返排，易在裂縫壁面和孔隙基質中發生滯留，減小甚至堵塞流動通道[6-8]，對儲層造成二次傷害，這種情況對于壓力系數低、黏土礦物含量高、水敏性強的儲層尤為明顯[9]，影響后期生產效率。同時，壓裂液存留于地層中也會污染地下環境，不符合環保理念[10-11]。因此，無論從環保還是從提高生產效率的角度，合適的返排程序顯得尤為重要。

在壓裂液返排設計與施工中，生產中往往采用裂縫強制閉合技術，實施強制閉合技術的壓裂井約占70%以上[12]，因此需要構建裂縫強制閉合模型。李勇明等[13]、汪翔[14]、Behr等[15]基于達西滲流原理建立了壓裂液濾失的二維模型，并依據物質平衡原理建立了裂縫強制閉合模型，模擬了不同噴嘴尺寸下井口壓力的變化規律。胡景宏等[16-17]、趙英杰[18]對流體壓力沿程損失量加以考慮，取得了更為準確的井口壓降曲線。Zhang等[19]針對多層裂縫性致密油藏地層，建立了相關理論預測模型，進一步豐富了裂縫強制閉合模型。

但上述研究將水力裂縫假設為平直裂縫，采用平均寬度[20]來描述裂縫寬度變化并計算相關物理量，不能客觀反映裂縫實際形態，同時缺少壓裂液在裂縫內部的流動描述，忽略了流體流動所需遵循的流動方程。基于此，提供了一種新的計算方法，基于邊界元方法構建返排模型，并結合流固耦合思想，將冪律流體平板流動方程與邊界元固體變形方程聯立求解，得到了返排過程中裂縫各處的寬度、流量、流體壓力的變化情況，以及相應壓降曲線與規律，旨在豐富和完善裂縫強制閉合理論模型，為實際生產與設計提供參考與借鑒。

1 邊界元方法簡介

如圖1所示，一條有限長度直線裂縫可分為上表面y= 0+和下表面y= 0-，裂縫的位移不連續量可定義為上下兩面的位移之差。

Di=ui(x,0-)-ui(x,0+)，i=x,y

(1)

式(1)中：ux、uy分別為切向和法向位移，m；切向位移不連續量Dx表示裂縫上下表面相對滑移量，法向位移不連續量Dy表示裂縫寬度。

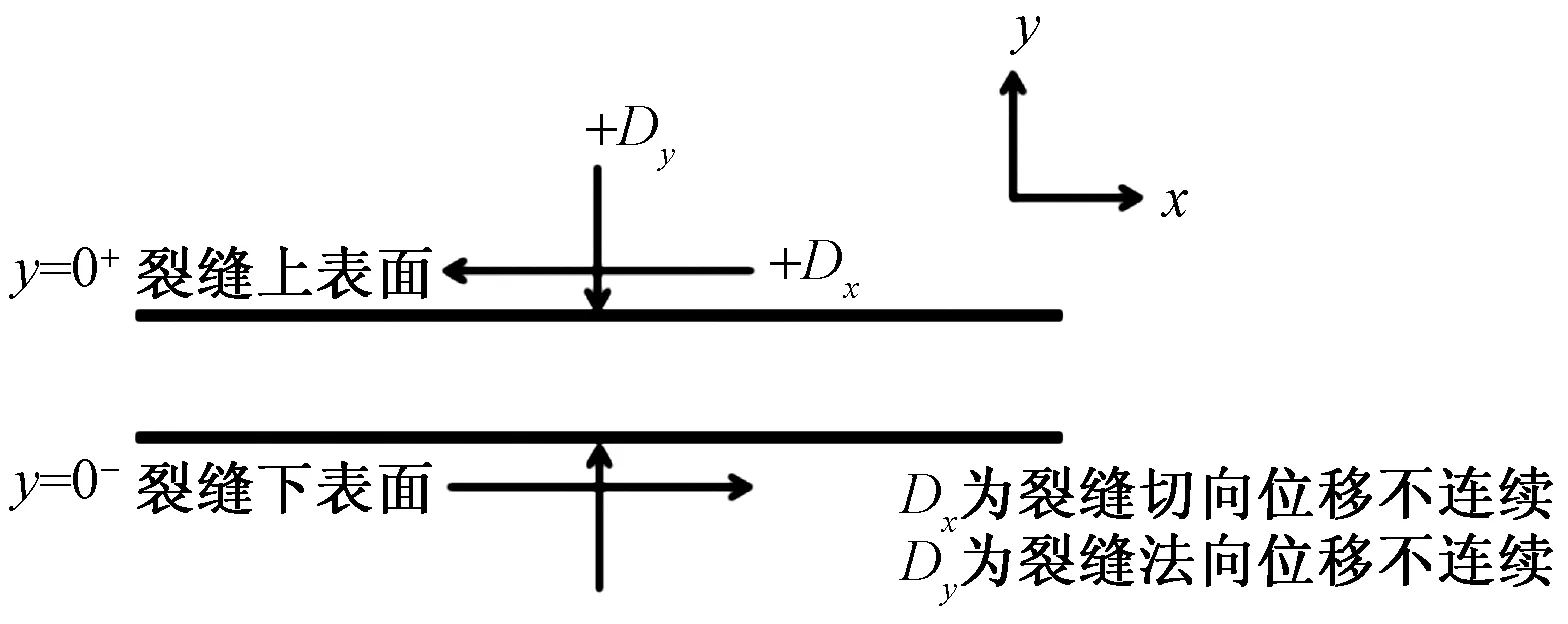
圖1 常位移直線裂縫示意圖Fig.1 Straight line crack with constant displacement

假設均勻各向同性無限彈性體中存在一條任意形狀裂縫，裂縫的平面投影如圖2所示。

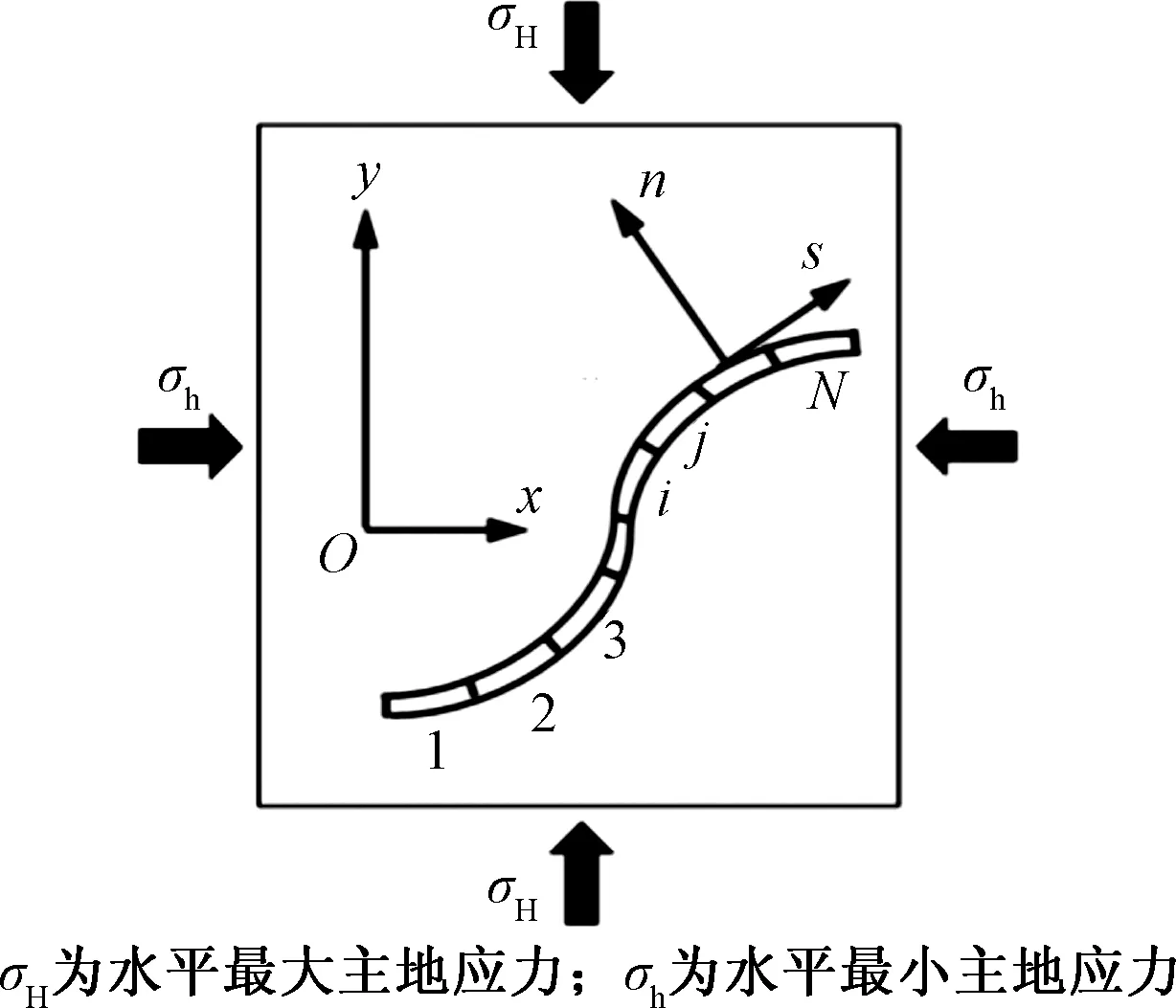
圖2 裂縫單元離散示意圖Fig.2 Discrete fracture elements

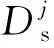
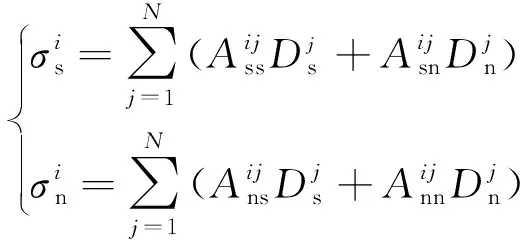
(2)

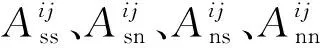
當張開的裂縫受到遠場地應力和裂縫內部流體壓力共同作用時，根據應力平衡方程，單元上應力邊界條件[22]為

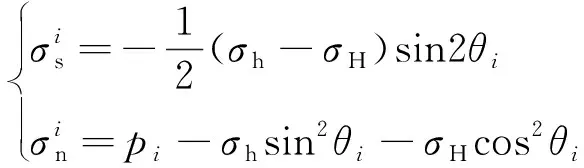
(3)

式(3)中：θi為裂縫單元i與坐標系x軸正方向的夾角，rad；pi為作用在裂縫單元i上的流體壓力，Pa。

將式(3)代入式(2)，可得邊界元固體變形方程組式(4)為

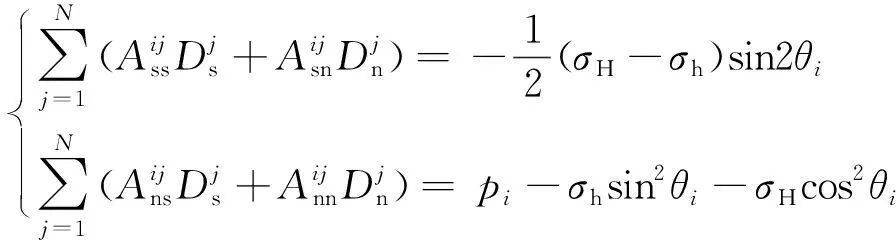
(4)

當已知地應力及裂縫中流體壓力分布時，求解該方程組即可得到各單元的位移不連續量，從而得出整條裂縫寬度分布。

2 返排過程數值建模

2.1 幾何模型

裂縫形態采用KGD(khristianovic-Geertsma-deklerk)模型[23]，假設水力裂縫為等高裂縫，其水平橫截面滿足平面應變條件。巖層經水力壓裂后，所形成的裂縫空間分布形態如圖3所示。

根據圖3，截取裂縫橫截面進行研究，考慮到問題的對稱性，選取半長裂縫作為研究對象，劃分單元如圖4所示。

2.2 數學模型與理論推導

根據第1節中邊界元理論，水力裂縫的寬度分布需滿足1對邊界元固體變形方程組式(4)。

另一方面，為確定流體流量、濾失量與裂縫體積增量之間的關系，從圖4中任取一裂縫單元i作為研究對象，如圖5所示。

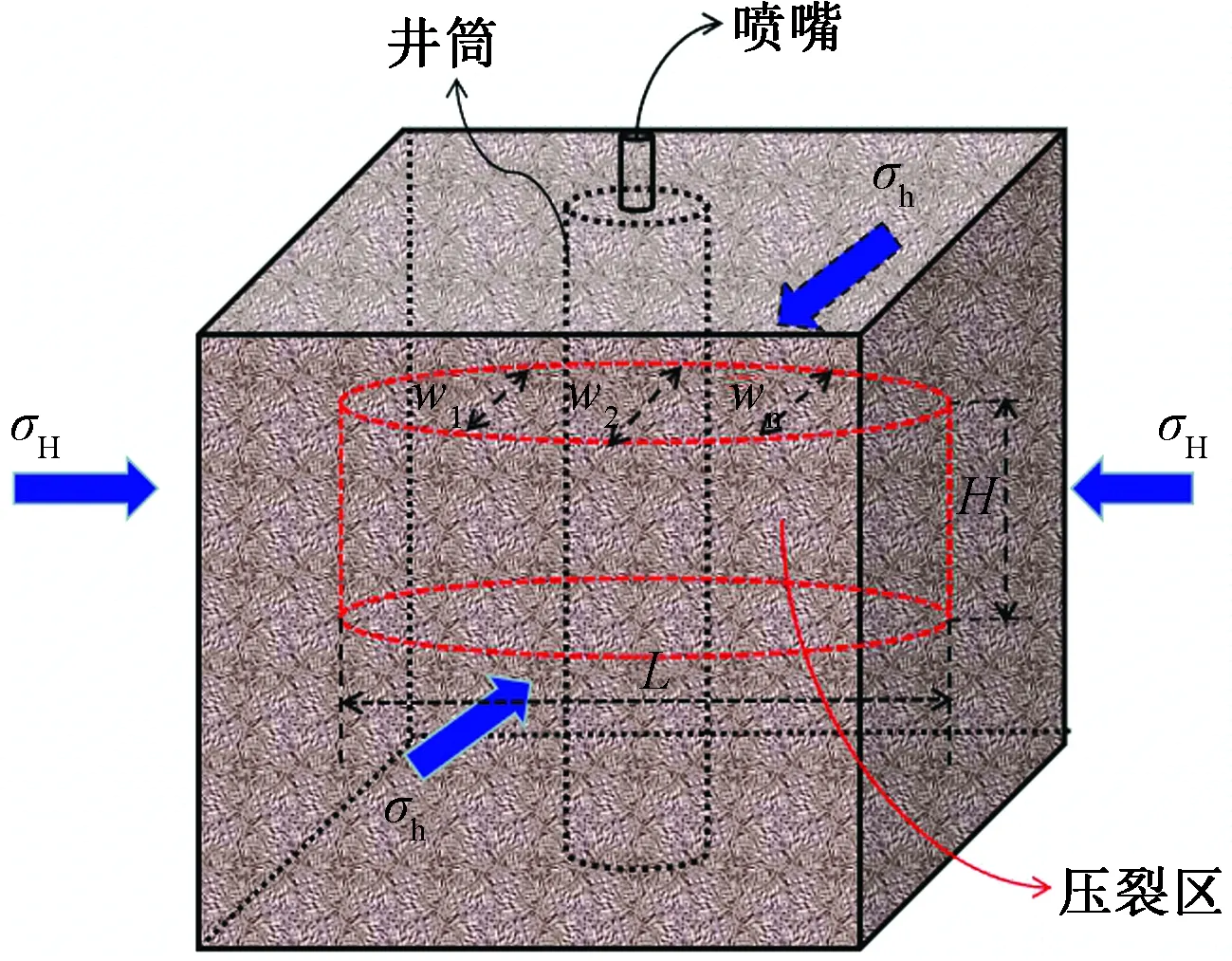
圖3 返排模型示意圖Fig.3 Diagram of fracturing fluid flowback model

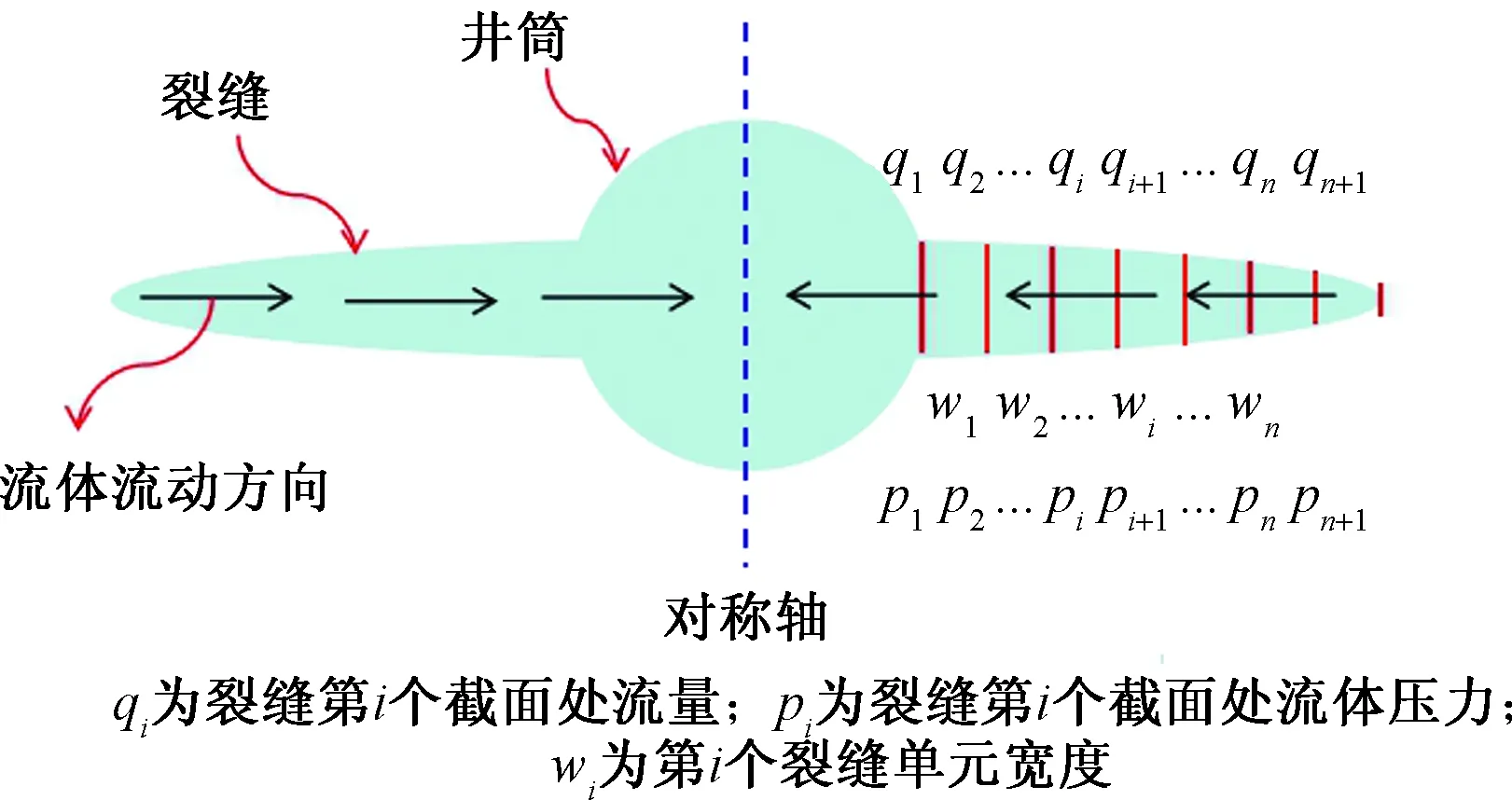
圖4 水力裂縫單元離散示意圖Fig.4 Diagram of hydraulic fracture discrete elements

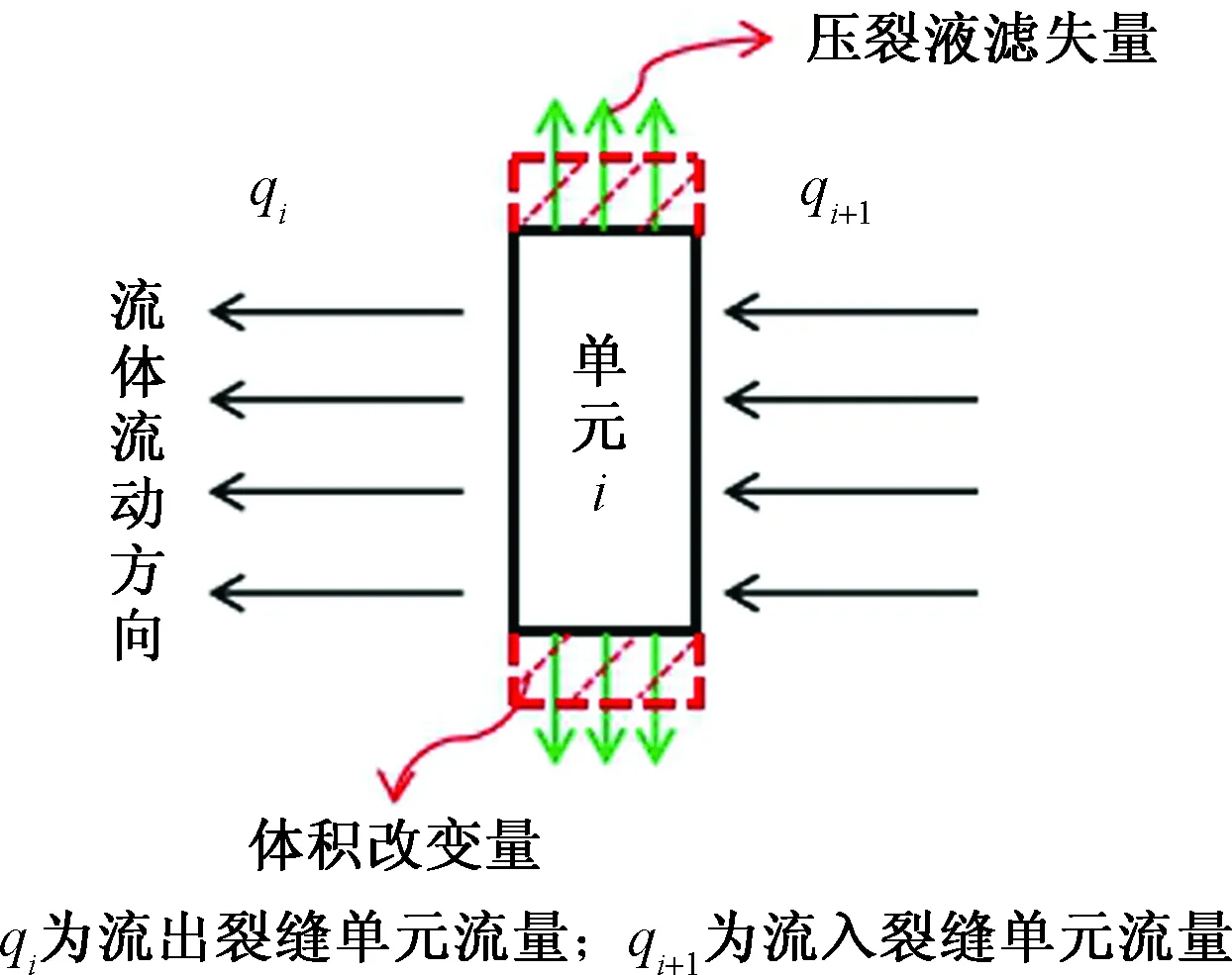
圖5 裂縫單元物質平衡過程Fig.5 Material balance process of a crack element

根據物質平衡原理，針對任一單位長度裂縫單元，增量時間內需滿足：流入該單元凈流量等于壓裂液濾失量與裂縫體積增量之和，即

(5)

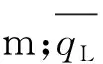
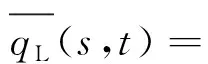
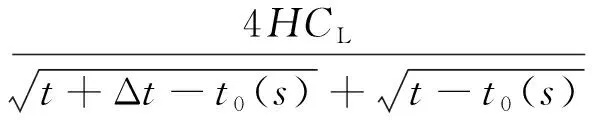
(6)

式(6)中：CL為壓裂液濾失系數，m/s0.5；t0為壓裂液沿壁面初始濾失時間，s。

同時，壓裂液在裂縫中的流動需滿足流體流動Navier-Stokes方程，流體在一對表面光滑的平板中流動時，Navier-Stokes方程[25]簡化為

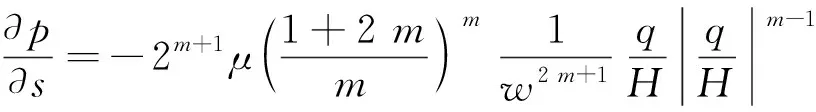
(7)

式(7)中：m為流體冪律指數；μ為壓裂液破膠黏度，Pa·s。

最后，返排模型需滿足以下邊界條件：

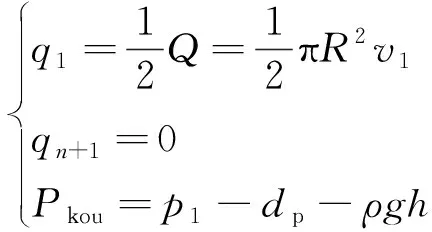
(8)

式(8)中：Q為壓裂液返排量，m3/s；R為井筒半徑，m；v1為井筒中流體流速，m/s；Pkou表示井口壓力，Pa；dp表示壓裂液在井筒中流動時的沿程損失，Pa；ρ為壓裂液密度，kg/m3。

式(8)中，為確定返排過程中不同時刻返排量Q(t)，可利用伯努利方程式(9)及連續性方程式(10)導出，即

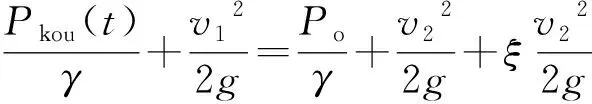
(9)

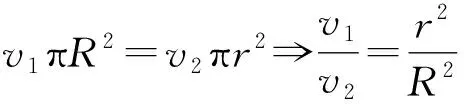
(10)

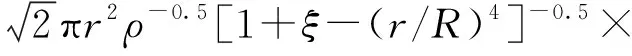
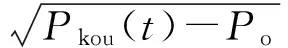
(11)

式中：γ表示壓裂液的重度，N/m3；v2表示壓裂液在噴嘴處流速，m/s；Po表示大氣壓強，Pa；r為噴嘴半徑，m；ξ表示局部阻尼系數。

式(8)中，壓裂液在井筒中的流動可視為圓管流，沿程損失量dp為[26]

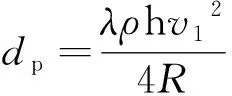
(12)

式(12)中：h為沿程路徑，即井深，m；λ為沿程阻力系數。

為確定沿程阻力系數λ，當流體為牛頓流體時，λ的表達式[27]為

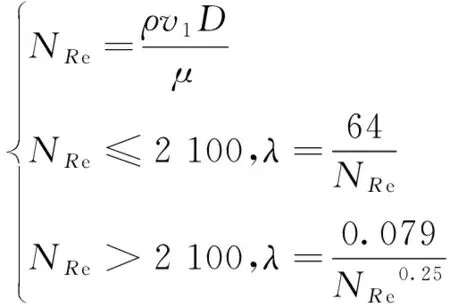
(13)

式(13)中：NRe表示流體雷諾數，用于判斷流體流態；D為井筒直徑，m。

將邊界元固體變形方程[式(4)]、體積平衡方程[式(5)]、流體流動方程[式(7)]與邊界條件[式(8)]聯立，構成大型非線性方程組，并采用牛頓迭代法加以求解。

2.3 數值解法與方法驗證

為采用牛頓迭代法進行數值計算，需確定方程組解的初值，初值恰當與否會影響到后續迭代的收斂性。考慮到停泵時裂縫的寬度、流體壓力及流量分布是后續迭代計算的初始條件，擬采用停泵時各變量分布作為初值解，并將停泵時裂縫寬度數值解與解析解進行對比，以驗證邊界元方法的可行性。

根據彈性力學理論，均衡受壓條件下的線裂縫寬度分布的解析解[22]為

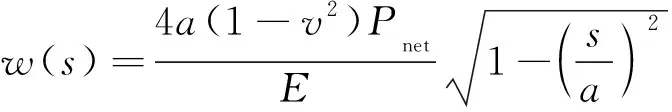
(14)

式(14)中：E為巖石彈性模量，Pa；Pnet為流體凈壓力，即流體壓力與最小水平地應力之差，Pa；a為裂縫半長，m。

根據邊界元理論式(4)，代入相關參數解得停泵時刻裂縫寬度數值解，并將此解與解析解進行對比，如圖6所示。

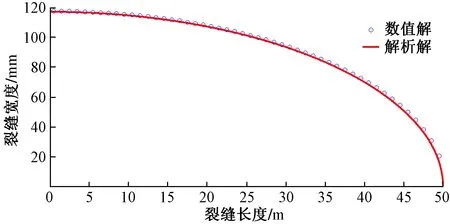
圖6 裂縫寬度數值解與解析解對比Fig.6 Comparison of width numerical and analytical solutions

可見用邊界元方法求解得到的數值解與解析解吻合良好，保證了邊界元方法的可行性。數值計算中采用的各物理量及參數如表1所示。

3 計算結果與分析

3.1 固定噴嘴返排過程描述

以噴嘴尺寸r=9 mm的情況為例，在固定時間間隔30 min下，裂縫閉合過程如圖7所示。裂縫寬度參量[圖7(a)]：藍色曲線為裂縫初始寬度分布，隨著壓裂液的排出，縫寬曲線逐漸下移，表明裂縫寬度逐漸減小，裂縫逐漸閉合；流體壓力參量[圖7(b)]：隨著壓裂液逐漸排出，裂縫內部流體壓力隨時間整體降低，同時流體壓力從縫踵(近井筒處)至縫趾(縫尖處)呈現出逐漸上升的趨勢，如圖8所示，但由于裂縫寬度較寬，壓裂液在縫中流動相對容易，流動壓降并不明顯，該壓降改變與壓裂液本身流體壓力相比不在同一個數量級；流量參量[圖7(c)]：沿縫長方向，由于裂縫寬度越發狹窄，流量也越來越小，且隨著壓裂液的排出，流量分布隨時間整體降低。當井口壓力減小為大氣壓時，意味著返排的結束，此時裂縫中及井筒內的壓裂液不再流動，流量降為0，井底流體壓力保持不變，裂縫寬度不再變化。

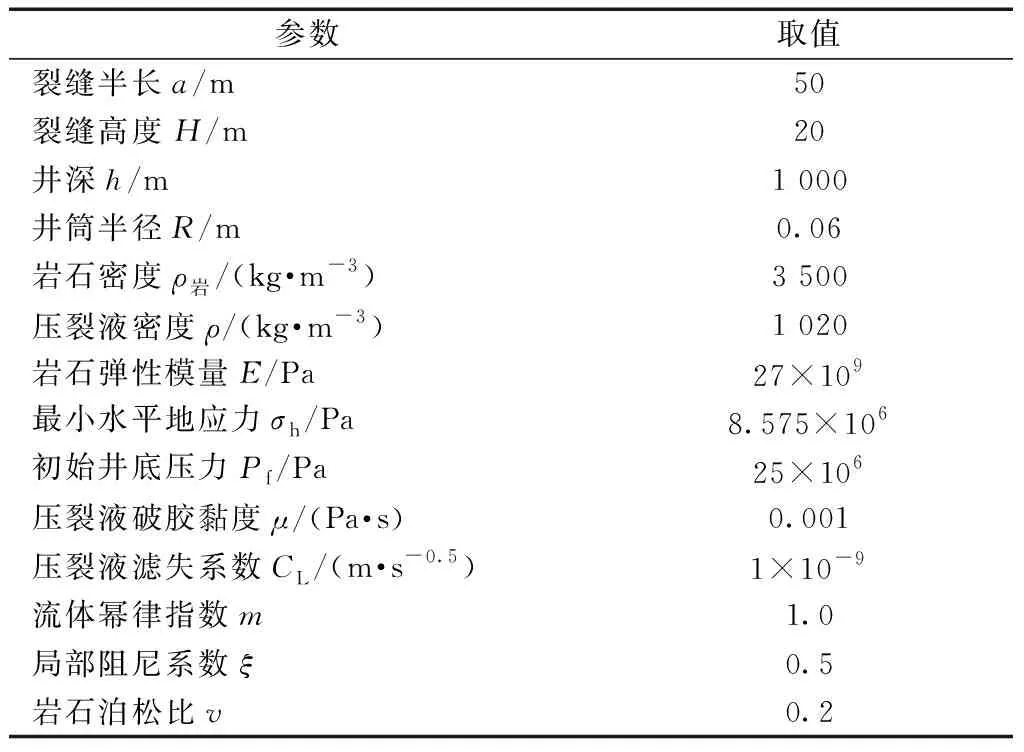
表1 數值計算中采用的各物理量

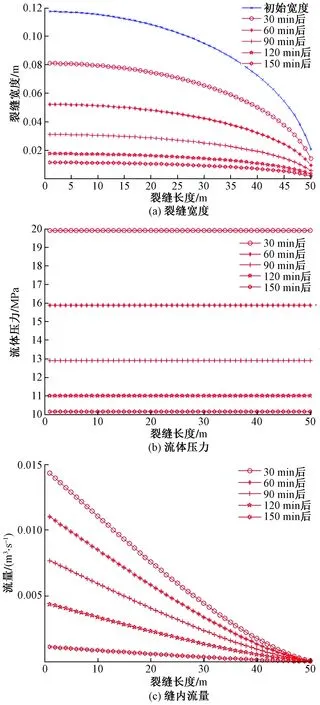
圖7 裂縫閉合過程各變量變化情況Fig.7 Variation of variables in the whole flowing-back process

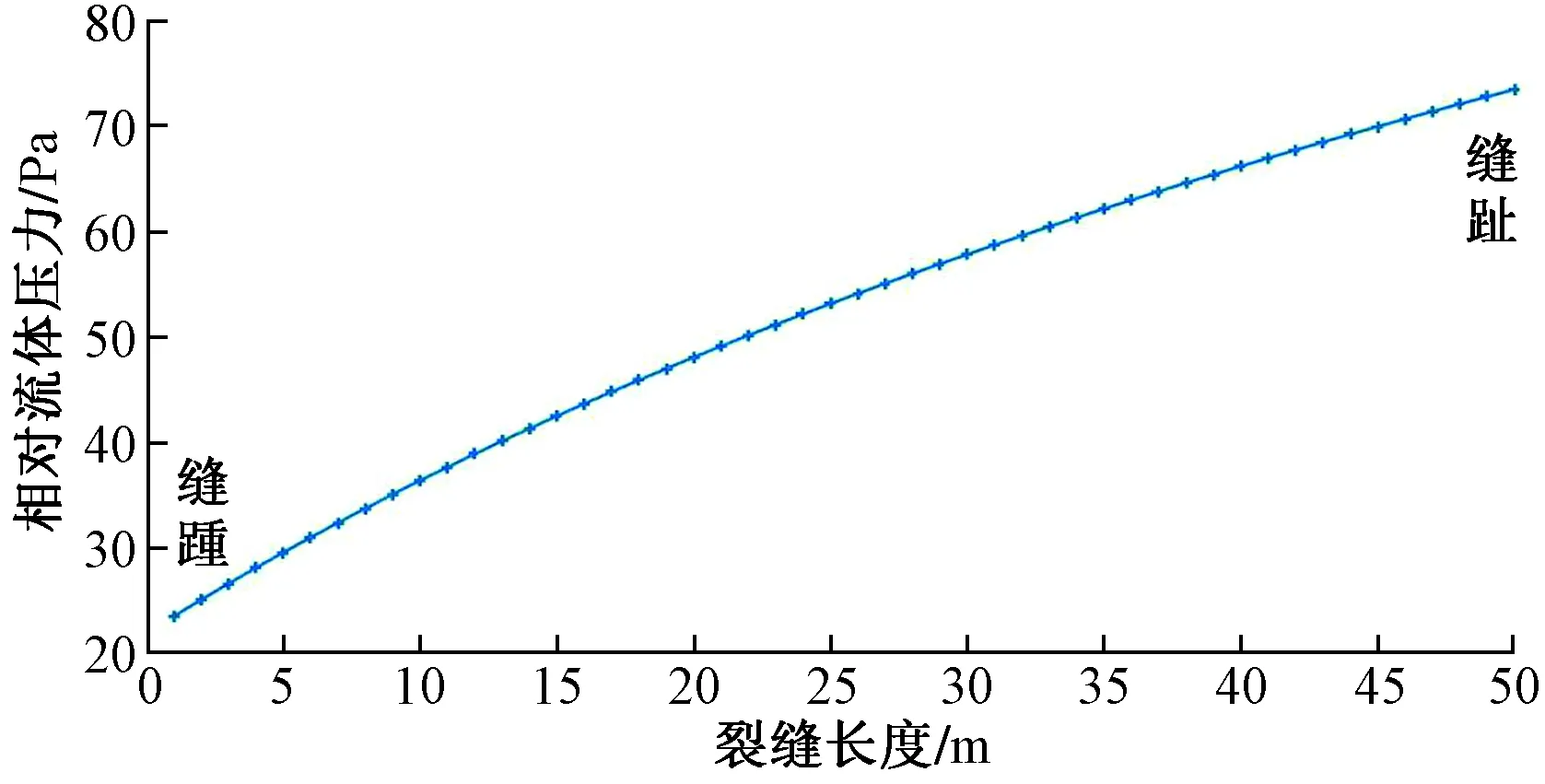
圖8 30 min時刻流體壓力沿縫長變化趨勢圖Fig.8 Trend of fluid pressure along fracture length at t=30 min

3.2 固定噴嘴返排過程壓降曲線

在生產實際中，對于壓裂液返排過程，獲取井口壓降曲線是關鍵性工作之一，準確的壓降曲線對于判斷返排是否已完成以及確定切換噴嘴的時機都至關重要，多種噴嘴尺寸下的井口壓降曲線如圖9所示。圖9中各條壓降曲線形勢相似，曲線斜率逐漸減小，井口壓力在返排初期下降較快，返排后期降速減慢。且隨著噴嘴尺寸的增大，壓降曲線斜率明顯增大，返排的時間明顯縮短，最終均表現為當井口壓力降為大氣壓時，返排結束，井口壓力維持不變。

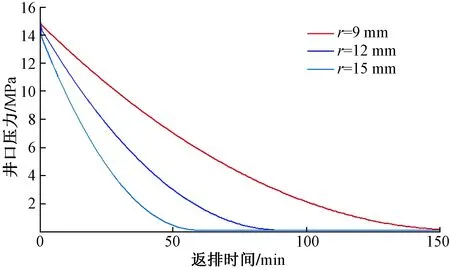
圖9 不同噴嘴尺寸下井口壓降曲線Fig.9 Pressure curve at wellhead with different nozzle sizes

3.3 變動噴嘴返排過程描述

在返排作業中，往往需要針對返排進程的不同，尋找合適的時機更換相應的噴嘴尺寸。在返排初期，盡量使用小噴嘴返排，控制裂縫閉合速度，避免支撐劑因返排速度過大被攜出；至返排后期，裂縫寬度下降到一定程度時，可認為支撐劑受到壁面約束，將不會再被壓裂液攜出，可用更大尺寸噴嘴加快返排，防止壓裂液對儲層的污染，降低儲層傷害。基于上述原則開展了相關數值模擬實驗，以了解變噴嘴條件下井底裂縫閉合過程及各變量變化情況，以噴嘴尺寸從r=6 mm調整至r=12 mm為例，結果如圖10、圖11所示。

圖10表示返排前期采用小噴嘴(r=6 mm)返排時的返排規律，以藍色曲線簇為代表。圖10(a)顯示，小噴嘴下裂縫閉合速度相對緩慢；圖10(b)顯示，小噴嘴下縫內流體壓力下降相對緩慢；圖10(c)顯示，由于噴嘴尺寸有限，裂縫中總體流量不高。

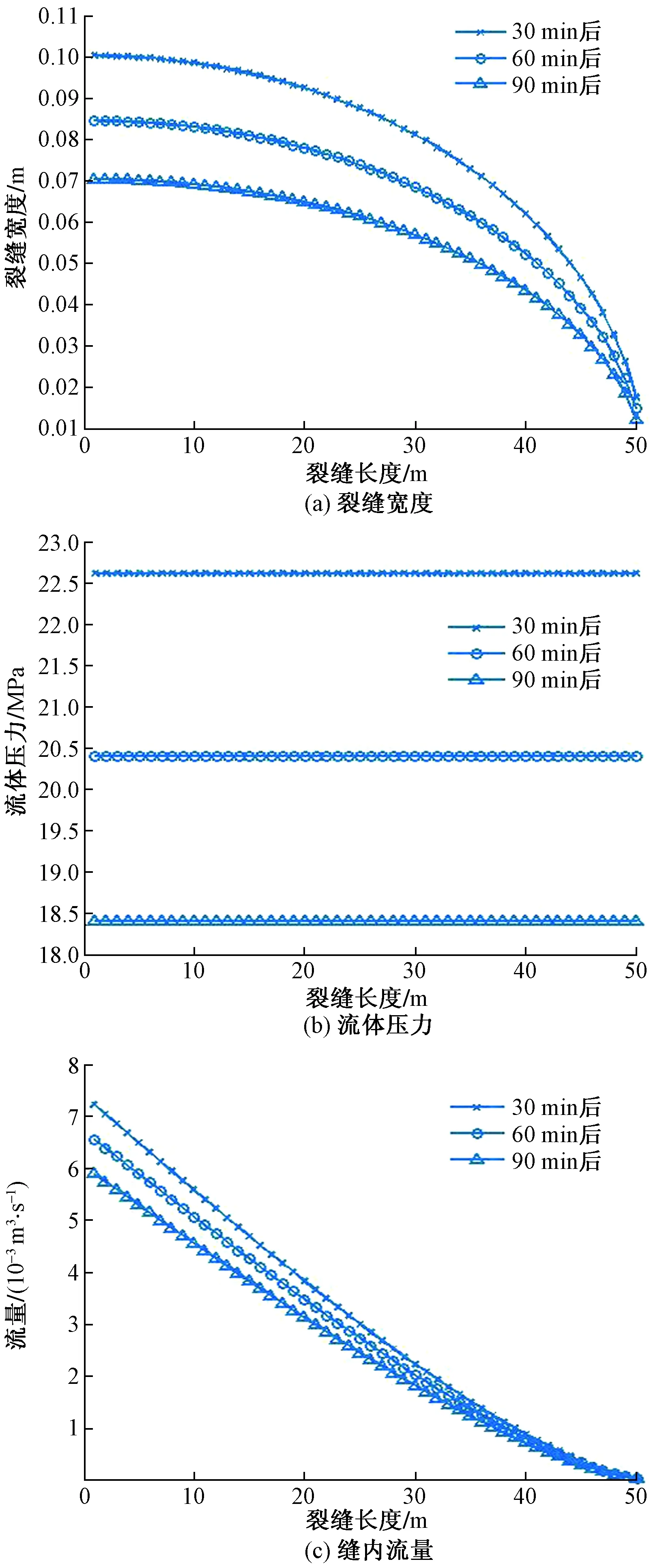
圖10 小噴嘴返排過程(r=6 mm)Fig.10 Flowback process at small size nozzle(r=6 mm)

圖11 大噴嘴返排過程(r=12 mm)Fig.11 Flowback process at big size nozzle(r=12 mm)

圖11表示后期換用大噴嘴(r=12 mm)各變量的重新分布情況，以紅色曲線簇為代表。換用大噴嘴后，裂縫寬度[圖11(a)]在原來基礎上繼續下降，且下降幅度相比于小噴嘴更大，流體壓力[圖11(b)]的變化也呈現出相似規律，表明更換大噴嘴后，裂縫閉合得更快。但流量的變化有所差異，如[圖11(c)]所示，換用大噴嘴后，縫中各單元流量均產生了顯著上升，表明更換大噴嘴后，井筒中流速有所增加，造成了流量的增長，意味著更多的壓裂液被排出，此流量的增長也是能夠加速返排進程的根本原因。且在大噴嘴尺寸下，縫中流量下降速率更大，隨著返排的后續進行，流量開始減小，逐漸將小噴嘴流量曲線“覆蓋”，隨著井口壓力逐漸降為大氣壓，流量也逐漸減小為0。

3.4 變動噴嘴返排過程壓降曲線

相應地，變噴嘴情況下井口壓降曲線如圖12所示。圖12中紅色曲線為參考基線，表示全程采用小噴嘴時井口壓降曲線，此時返排時間較長。分別模擬了噴嘴尺寸從r=6 mm調整至r=9 mm、r=12 mm、r=15 mm時的返排過程，前半部分曲線噴嘴尺寸較小時，井口壓力下降相對緩慢，曲線斜率較小，換用大尺寸噴嘴時，曲線產生了明顯拐點，曲線斜率顯著增大，返排速率大幅加快，既滿足返排初期返排速率不宜過大的要求，又滿足返排后期盡可能加速返排的要求，該模式下的壓降曲線對實際生產具有一定借鑒意義。

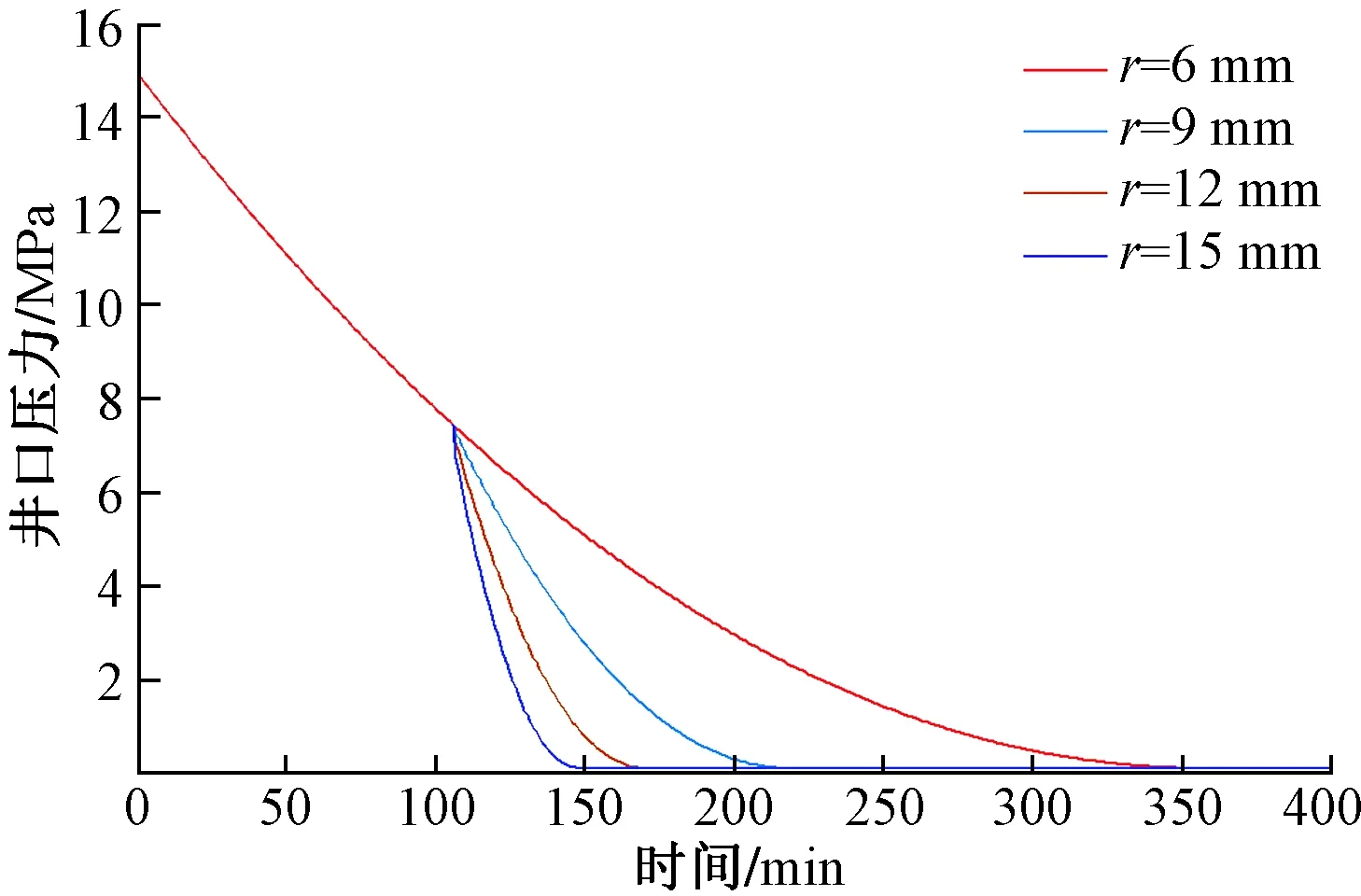
圖12 變噴嘴情況下井口壓降曲線Fig.12 Pressure curve at wellhead with variable nozzles

4 結論

以往壓裂液返排研究中，多假設裂縫寬度不隨縫長的延伸而變化，借助邊界元方法，綜合考慮了返排過程中的濾失量、沿程損失、返排終止判據、井底井口壓力之間的關系等因素，完成了數值建模，構建了非線性方程組并完成了求解，對于裂縫寬度、縫內流量及流體壓力的實際分布和變化過程進行了量化計算與描述，得到了各變量變化規律及相應壓降曲線，相比于傳統模型精度更高。

(1)裂縫延伸越深，裂縫寬度越窄，縫內流量越小，且隨著壓裂液排出，裂縫逐漸發生閉合，裂縫寬度逐漸減小，縫內流體壓力整體降低。在返排進程中增大噴嘴尺寸，會加速裂縫閉合，單位時間內裂縫寬度及流體壓力下降幅度更大，但此時縫中各單元流量均發生了顯著上升，這意味著更多的壓裂液被排出。

(2)對于固定尺寸噴嘴，井口壓降曲線表現為先陡后緩。返排初期壓裂液回流較快，壓降曲線下降較快，隨著返排進行，壓裂液能量逐漸耗散，壓裂液回流減慢，壓降曲線斜率不斷減小，當井口壓力降為大氣壓時，返排停止。同時，對比多種尺寸的固定噴嘴，噴嘴尺寸的些許改變對返排時間影響巨大，噴嘴尺寸增大將導致壓降曲線斜率明顯增大，返排時間明顯縮短。

(3)對于變動尺寸噴嘴，井口壓降曲線表現為先緩后陡。返排前期采用小噴嘴返排時，壓降曲線斜率相比于后期更小，單位時間內壓力下降相對緩慢，此時返排速率得到了人為控制，避免了支撐劑因返排速度過大被攜出。后期換用大噴嘴時，壓降曲線產生了明顯拐點，曲線斜率顯著增大，返排速率明顯加快，人為加速了返排進程，避免了壓裂液對儲層的污染。研究成果可供實際生產參考與借鑒。