高強度發動機螺栓軸向應力的測量
趙新玉,王英華,張佳瑩
(大連交通大學 材料科學與工程學院,大連 116028)
螺栓是一種利用螺母與螺紋產生的緊固應力對結構進行連接的工具,廣泛應用于船舶、建筑、車輛、航空航天等領域,而螺栓的軸向預緊力是影響螺栓壽命以及使用狀態的重要因素[1]。雖然采用超聲單縱波測量技術也能夠有效得到螺栓的軸向應力,但該法需要測量螺栓的原始長度,故發動機上無法拆卸的螺栓不能使用該測量法[2]。
目前,采用超聲波對螺栓進行應力分析的研究有很多。趙春華等[3]提出使用超聲技術在線實時檢測風電機組螺栓的軸向應力;韓玉強等[4]對使用聲彈性法測量螺栓的影響因素進行了研究;何存富等[5]研究了溫度對測量精度的影響;賈雪等[6]詳細論述了基于聲彈性理論的超聲螺栓應力測量原理,同時研究了溫度對波速的影響。綜上所述,各國的學者對超聲波螺栓載荷的測量方法均進行了深入研究,但還是無法解決單縱波對已緊固螺栓和未知長度螺栓的測量問題。
筆者采用聲彈性理論的橫縱波無損測量方法,建立了超聲橫縱波螺栓測量系統,并通過采用橫縱波一體化探頭以及1 GHz的高頻數據采集卡提高了測量精度和穩定性。對發動機缸體及軸承上的高強度螺栓進行了實際軸力測量,并與預加載軸力進行對比,驗證了系統測量的準確性。
1 超聲測量螺栓應力的原理
考慮微小質點沿x軸振動(縱波)的情況,彈性固體中一維平面縱波通過力學平衡得到(只x方向變化,F=ma)
(1)

(2)
式中:dx,dy,dz均為體積;σx為應力;ρ為密度;μx為位移;t為時間。
另外,材料本構方程為

(3)
式中:εx,εy,εz分別為x,y,z方向的應變;σy,σz分別為y,z方向的應力;ν為泊松比;E為拉壓彈性模量。
式(3)中的第一個式子可以寫成

(4)
螺栓的約束條件為σy=σz=0,則式(4)可寫為
εx=σx/E
(5)
整理得

(6)
由式(6)可知
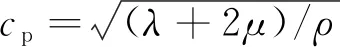
(7)
式中:λ,μ為拉梅常數;cp為縱波聲速。
當考慮橫波的情況時,本構方程為
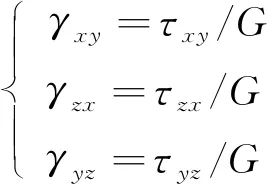
(8)
式中:γ為剪切應變;τ為剪切應力;G為剪切彈性模量。
(9)
螺栓的約束條件為γxy=γyz=0,則式(8)為
γzx=τzx/G
(10)
將式(9)代入式(10)得
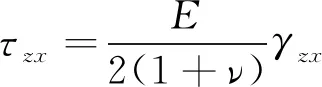
(11)
由式(11)可知
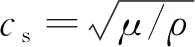
(12)
式中:cs為橫波聲速。
根據聲彈性理論[7],固體中的聲速與應力的關系為
(cσ,p)2=(c0,p)2-
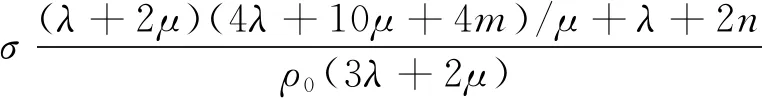
(13)
(cσ,s)2=(c0,s)2-
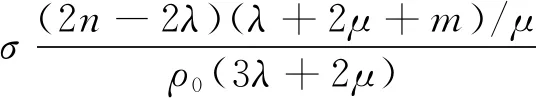
(14)
式中:σσ,p和cσ,s為有應力下的縱波聲速和橫波聲速;c0,p和c0,s為無應力下的縱波聲速和橫波聲速;m,n為三階彈性常數。
令
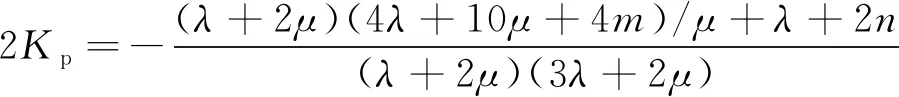
(15)
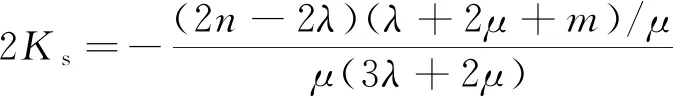
(16)
式中:Kp,Ks為自定義常量。
m,n為三階彈性常數,則
(cσ,p)2=(c0,p)2(1+2Kpσ)
(17)
(cσ,s)2=(c0,s)2(1+2Ksσ)
(18)
設螺栓未受應力且溫度為t0,當溫度為t且未受應力時,縱橫波在螺栓中傳播的聲時T0,p,T0,s分別為
T0,p=2L0[1+β(t-t0)]/ct,p
(19)
T0,s=2L0[1+β(t-t0)]/ct,s
(20)
式中:β為螺栓的溫度膨脹系數;L0為螺栓在溫度為t0時的長度。
ct,p=c0,p(1-αpΔt)
(21)
ct,s=c0,s(1-αsΔt)
(22)
式中:ct,p為橫波受應力σ且溫度為t0時的聲速;ct,s為縱波受應力σ且溫度為t0時的聲速;αp,αs為縱波和橫波聲速隨溫度變化的聲速系數;Δt為溫度差。
設橫縱波在不受應力時的T0,p和T0,s的比值為M,則
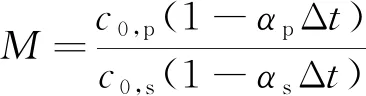
(23)
由于αp,αs非常小,約為10-4數量級,所以當溫差不是很大時,M近似為一條直線。
螺栓中傳播的聲時為受力及不受力部分聲時的和,縱波受力時的聲時Tp為
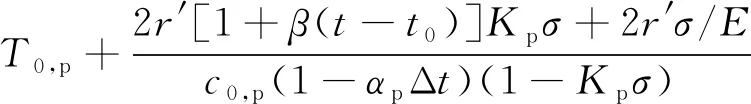
(24)
式中:c(σ,t),p為縱波受應力σ且溫度為t時的聲速;r′為螺栓有效夾緊距離。
c(σ,t),p=(1-αpΔt)cσ,p
(25)
r′=r+r1+r2
(26)
ΔL=L0-r′
(27)
r′(有效夾緊距離)=螺帽的+螺母的+夾緊長度。
同理可知
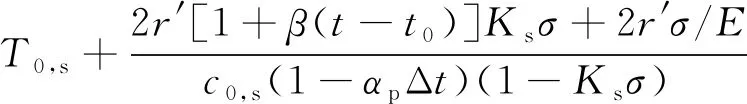
(28)
σ=
(29)
式中:Ts為橫波受力時的聲時。
由于Kp,Ks約為10-11,10-12的數量級,因此式(29)可簡化為
σ=K(r)(TpM-Ts)
(30)
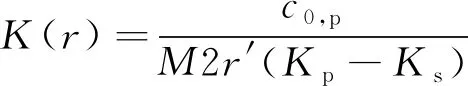
(31)
利用拉伸機和扭力機標定出螺栓軸力與橫縱波躍度時間之間的關系,利用式(30)求出K(r)并擬合成曲線,保存在計算機中。實際測量時只需測量出緊固后螺栓的橫波聲時與縱波聲時,依據保存的擬合曲線就可以求出此時螺栓的軸向應力。
2 試驗平臺
具有獨特設計且橫縱波一體的超聲換能器(內環縱波,外環橫波)實物如圖1所示,換能器橫波單元與縱波單元相互獨立,且可由系統控制進行激勵,中心頻率為2.5 MHz,直徑為12 mm。

圖1 橫縱波一體的超聲換能器實物
被測缸體高強度螺栓的材料為35CrMoV,軸承高強度螺栓分為A款和B款。栓體直徑為13 mm,為了獲得更強的回波信號,需要對螺栓上下底面進行打磨,使用調制蜂蜜為耦合劑,試驗溫差小于5 ℃。螺栓型號參數如表1所示。

表1 螺栓型號參數
整套測量系統的試驗裝置由兩部分組成(見圖2),即施加應力部分和超聲測量部分。
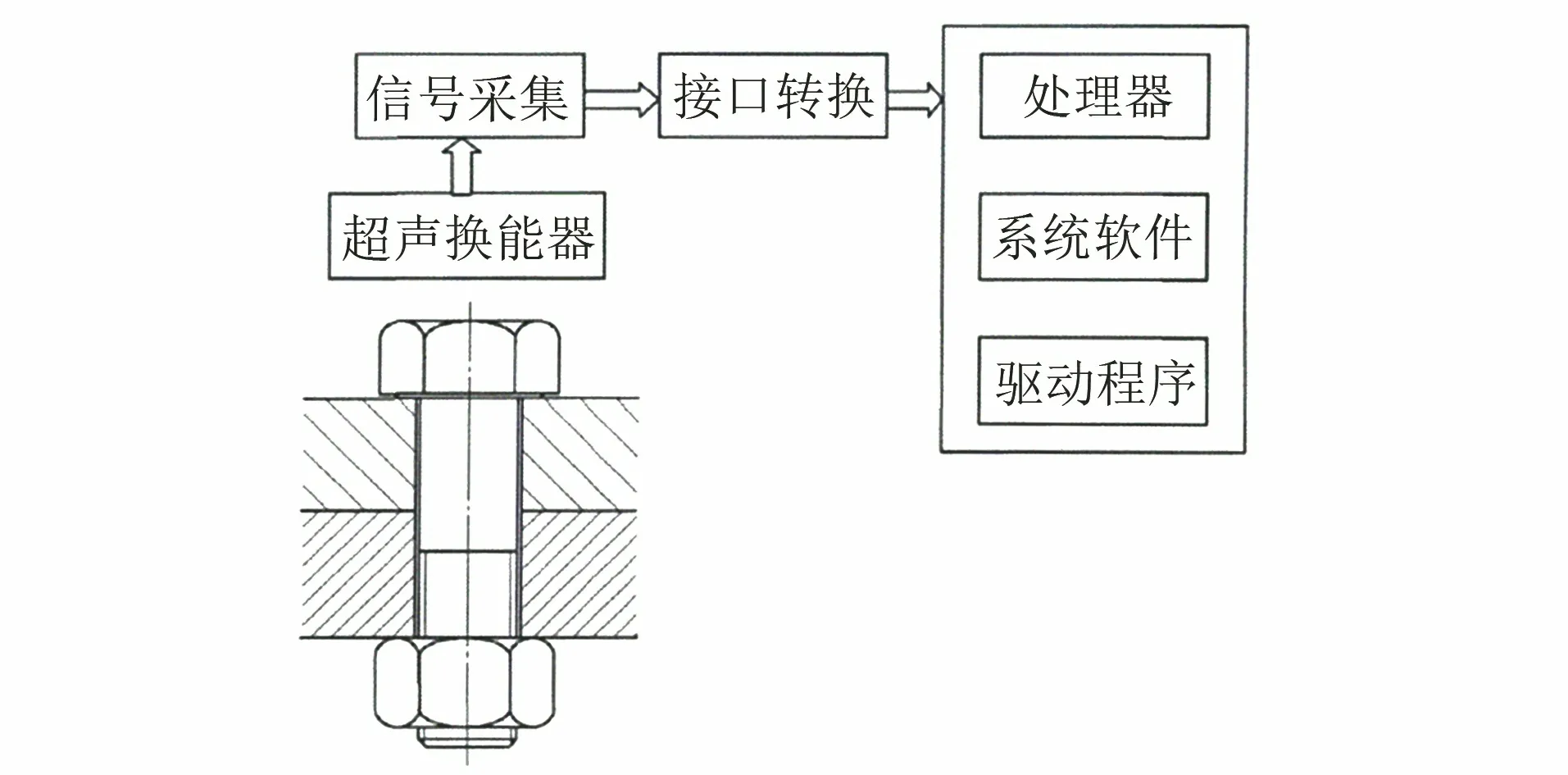
圖2 螺栓測量系統組成框圖
整套系統由橫縱波一體探頭、脈沖收發儀、數據采集卡、系統軟件等組成。系統的采樣頻率為1 GHz,采用橫縱波一體的超聲換能器,使用脈沖收發儀進行信號激勵,采用螺栓測量系統對超聲信號的躍度時間進行記錄,根據記錄的時間得出已緊固螺栓的軸向應力。
3 系數測量與實測結果
標定時采用螺栓夾具對螺栓進行夾持,夾具螺孔長度與實測時的螺孔長度相同,模擬螺栓預緊工況。使用靜態液壓萬能試驗機MTS-C64.301進行精確地定量拉伸試驗,可以獲得準確的應力-聲時對應曲線。靜態液壓萬能試驗機的拉伸極限為300 kN,以10 kN為一個步進進行拉伸試驗。試驗結果均使用MATLAB軟件對被測螺栓的軸力和TpM-Ts進行擬合,并對擬合的直線進行F檢驗(顯著性檢驗)[8],檢驗結果說明聲時差與應力之間有良好的線性關系,發動機缸體與軸承的擬合曲線如圖3,4所示。
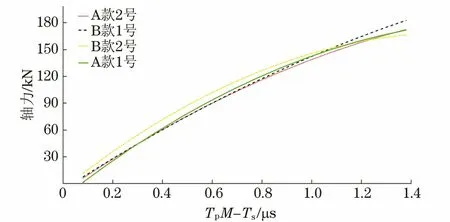
圖3 發動機缸體螺栓軸力與TpM-Ts擬合曲線
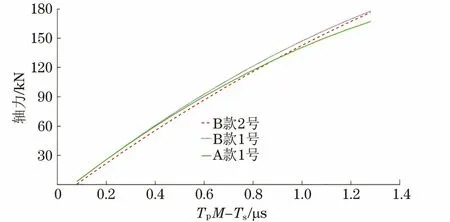
圖4 發動機軸承螺栓軸力與TpM-Ts擬合曲線
從圖3,4可以看出,是相同材料不同牌號的高強度螺栓在較低軸力載荷作用下的軸力與TpM-Ts的擬合曲線近似直線,但當加載軸力超過120 kN時,擬合曲線TpM-Ts的斜率開始發生變化。從拉伸對比圖可以看出,缸體B款螺栓比A款螺栓的數據曲線更加離散,表明A款螺栓之間的材料差異性更大,擰緊時軸力的離散也更大。將測定的數值儲存在計算機中,當實測已緊固螺栓應力時,可根據式(30)求出相應的軸力。實測軸承螺栓56根,包括28根A款軸承螺栓和28根B款軸承螺栓,預計發動機軸承螺栓加載的軸力為140 kN150 kN,發動機缸體螺栓加載的軸力為130 kN140 kN。實際系統測量結果如圖57所示。

圖5 A款軸承螺栓實測應力曲線
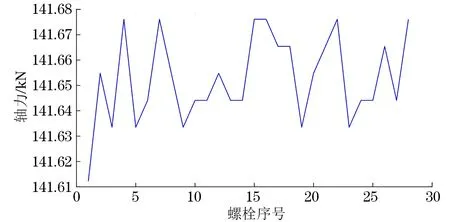
圖6 B款軸承螺栓實測應力曲線
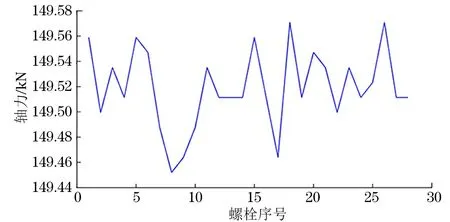
圖7 缸體螺栓實測應力曲線
由圖57可知,實測值與預加載力之間的差值較小,缸體螺栓不同位置處最大軸力與最小軸力的差值小于15 kN,同款軸承螺栓不同位置處的最大軸力與最小軸力的差值小于1 kN,滿足發動機螺栓測量精度要求。
4 結語
實際測量過程中,無需測量螺栓的伸長量以及螺栓全長,在螺栓軸向長度未知的情況下,可以測量栓體軸向應力。標定測量過程與實際測量過程均操作簡單,測量時間相對較短,測量效率較高。在高負荷加載下,螺栓軸向應力測量的實際值與理論值平均誤差小于5%。

