保險公司和再保險公司之間的停止損失再保險策略選擇博弈

林祥,錢藝平,任余豪

(浙江工商大學金融學院,浙江 杭州310018)

1.引言

再保險是保險公司分散經營風險,控制保險責任,提高承保能力的重要手段.保險公司購買再保險需要支付再保險保費,同時把一部分風險轉移給再保險公司.因此,保險公司向再保險公司購買再保險時,在承擔風險和獲得收益之間有一個替換,存在著價格和需求之間的一個博弈.在實際中,一個再保險合約是需要保險公司和再保險公司雙方同時認可并簽訂的,一個對保險公司最有利的再保險策略往往并不是對再保險公司最優的,甚至可能是再保險公司無法接受的.因此,在再保險實踐中,需要考慮以下問題:保險公司購買的最優再保險數量是多少或保險公司的最優自留風險是多少? 再保險公司對保險公司購買再保險時的再保費是多少?再保險公司的最優承保再保險數量是多少? 是否存在再保險合約使得保險公司和再保險公司都能受益?能成交的再保險合約需要滿足什么條件?

現有的文獻主要站在保險公司的角度研究最優再保險問題,Borch[1]指出一個對保險公司的最優再保險合約,對再保險公司來說并不是最優的.因此,一個合理的再保險合約需要同時考慮保險公司和再保險公司的利益.在靜態單期模型中,CAI等人[2]在不同的保費準則下,考慮了使得保險公司和再保險公司聯合生存和收益概率最大化的最優比例再保險和最優停止損失再保險合約設計問題.CAI等人[3]在最小化保險公司和再保險公司的VaR風險測度凸組合下,考慮了保險公司和再保險公司之間的最優再保險合約設計問題.LO[4]在再保險公司風險約束下,提出了使得保險公司扭曲風險測度最小的再保險合約設計方案.ZHANG等人[5]在保險公司和再保險公司效用增加約束下,運用最優化準則考慮了保險公司和再保險公司之間的最優比例再保險合約設計問題.JIANG等人[6]考慮了風險厭惡的期望效用最大化的保險公司和再保險公司之間合作再保險策略選擇博弈問題,在協商再保費和期望值再保費下,得到Pareto最優再保險合約.

近年來,也有大量的文獻研究連續時間保險公司和再保險公司之間的最優再保險合約設計問題.ZENG和LUO[7]通過隨機合作博弈框架表示保險公司和再保險公司之間的聯系,研究了使得保險公司和再保險公司的效用加權和最大化的Pareto最優再保險策略選擇問題.LI等人[8]在擴散風險模型下,考慮了使得保險公司和再保險公司期望終端財富效用乘積最大化的最優比例再保險和投資策略選擇問題,在保險公司和再保險公司都具有指數效用下,得到最優比例再保險和投資策略,以及值函數的顯示表達式.LI等人[9]考慮了保險公司和再保險公司的終端財富權重和的時間一致再保險和投資策略選擇問題,得到了時間一致再保險-投資策略,以及值函數的顯示解,并通過數值計算得到了模型參數對時間一致最優再保險和投資策略的影響.王愫新等人[10]和王愫新和榮喜民[11]同時考慮保險公司和再保險公司的最優再保險和投資問題,在保險公司和再保險公司終端期望財富效用最大化目標下,得到了保險公司和再保險公司的最優再保險和投資策略,以及值函數的顯示表達式.ZHAO等人[12]在風險股票價格服從CEV模型下,考慮了保險公司和再保險公司盈余過程的加權和的時間一致再保險-投資選擇問題,得到了時間一致再保險-投資策略和值函數的顯示解.

委托代理框架提供了一個描述保險公司和再保險公司之間相互作用的模型.HU等人[13]在保險者或再保險者索賠過程模型不確定下,從委托-代理框架考慮了連續時間比例再保險合約問題,得到最優再保險合約的顯示表達式.HU等人[14]在再保險公司索賠強度不確定下,從委托-代理框架考慮了保險公司和再保險公司之間的連續時間比例再保險和停止損失再保險策略選擇問題,得到最優再保險合約滿足的方程.結果顯示再保險公司降低再保險保費會增加再保險需求,但是再保險公司面臨的模型不確定會增加再保險公司的再保險保費.HU和WANG[15]在保險公司索賠強度不確定下,從委托-代理框架考慮了傳統風險模型的比例再保險和停止損失再保險合約問題,在指數效用函數和指數索賠分布下,得到再保險公司的最優再保費,保險公司的最優自留額,以及保險公司和再保險公司值函數的顯示表達式.CHEN和SHEN[16]在期望財富效用最大化下,考慮了保險公司和再保險公司之間的隨機leader-follower比例再保險博弈問題,在指數效用函數下,得到了再保險公司的最優再保費,保險公司的最優自留額,以及保險公司和再保險公司值函數的顯示表達式.GU等人[17]在再保險公司索賠強度和金融市場風險不確定下,考慮保險公司和再保險公司之間的停止損失再保險和投資策略選擇問題,在指數分布索賠和指數效用函數下,得到了該問題的顯示解.WANG和Siu[18]在保險公司面臨動態VaR風險限制下,研究了保險公司和再保險公司之間的魯棒再保險合約設計問題,在指數效用函數下,得到了該問題的顯示解.

現有文獻對保險公司和再保險公司之間再保險合約設計問題的研究,主要集中于保險公司決定購買再保險數量,再保險公司決定承保的再保險保費.而在再保險實踐中,還可能有保險公司決定購買再保險數量和再保險費,再保險公司只能根據再保費決定是否承保;或者再保險公司確定再保險保費和承保的再保險數量,保險公司只能根據再保費決定是否購買此數量再保險.現有的文獻也缺乏對保險公司和再保險公司的效用損益進行系統分析,保險公司購買再保險和再保險公司承保后,其期望盈余效用如何變化.模型主要參數變化如何影響再保險策略和再保費,如何影響再保險合約設計,這些問題都值得進行系統深入研究.本文將系統研究處于地位不對等的保險公司和再保險公司之間的停止損失再保險策略選擇博弈問題,探討再保險合約能夠成交的條件.同時,深入分析模型主要參數對再保險合約設計和值函數的影響,并探尋其內在保險意義.本文的結果有助于更好的理解保險公司和再保險公司之間的再保險博弈,對于再保險合約設計也有重要的理論和實際意義.

2.風險模型

令(?,F,{Ft}0≤t≤T,P)是一個滿足通常條件的完備概率空間,其中域流Ft表示到t時刻為止所能獲得的所有信息,T為一有限時間.假設下面所有的隨機過程都是定義在該完備概率空間上的適應過程.

根據經典的Cramer-Lundberg模型,保險公司盈余過程可表示為

其中x0≥0是保險公司的初始盈余,c >0是單位時間的保費收入,索賠次數過程{N(s),s ≥0}是參數為λ >0的齊次Possion過程,每一次理賠大小{Zi,i= 1,2,···}是獨立同分布的正值的隨機變量,分布函數為F(z),期望值為μ= E(Zi),二階原點矩為σ2= E[Z2i],矩母函數為mZ(r)=E[erZ].此外,假設{N(s),s ≥0}和{Zi,i=1,2,···}之間相互獨立.假設保險公司按期望值保費原理收取保費,即c=(1+θ)λμ,其中θ >0為保險公司的安全系數.

假設保險公司可以通過向再保險公司購買停止損失再保險來轉移風險,在這里不考慮投資.對每次賠付,假設保險公司的自留風險為m,即對每次賠付,保險公司負責賠付Zi ∧m,再保險公司負責賠付(Zi ?m)+.假設再保險公司也按期望值保費原理收取再保費,再保險公司的安全系數為η,則再保險公司的再保費為c1= (1+η)λE[(Zi ?m)+].此時,再保險價格就通過再保險公司的安全系數來體現,并假設η ≥θ.

因此,保險公司購買停止損失再保險后盈余過程為

假設再保險公司自身并沒有參與其它的保險活動,其收入來源完全由再保險保費構成.不考慮保險公司和再保險公司的投資行為,是因為我們希望探討保險公司和再保險公司之間再保險合約能夠成交的條件.再保險公司承保后(接受保險公司的停止損失再保險)的盈余過程為

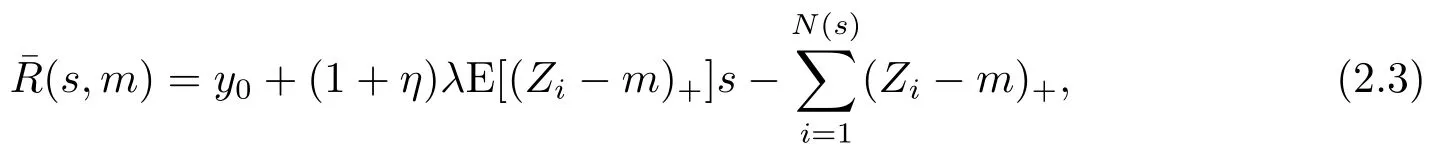
其中y0>0是再保險公司的初始盈余.

因此,根據Grandell[19]可得,保險公司的盈余過程可用下面的擴散過程逼近

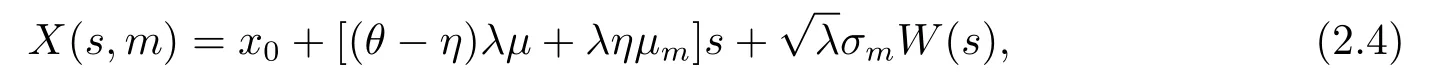
再保險公司承保后盈余過程的擴散逼近過程為

其中W(s)是一個標準的Brownian運動,并且

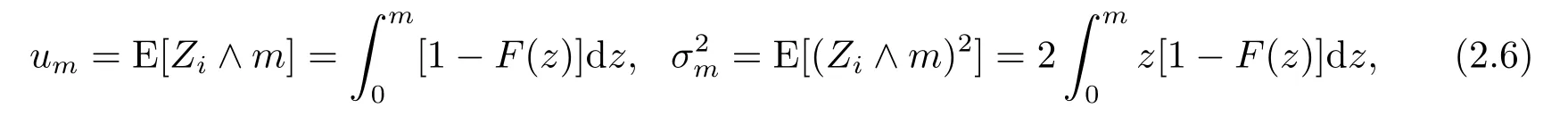
和

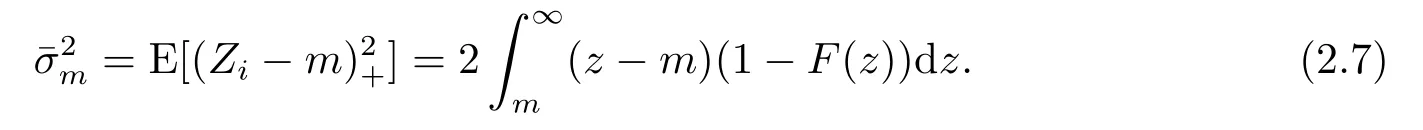
考慮兩個嚴格遞增嚴格凹的效用函數ui:R→R,i=1,2,即u′i >0且u′′i <0,其中u1為保險公司的效用函數,u2為再保險公司的效用函數.保險公司以期望盈余效用增加作為購買停止損失再保險的依據,保險公司在終端時刻T的期望盈余效用定義為

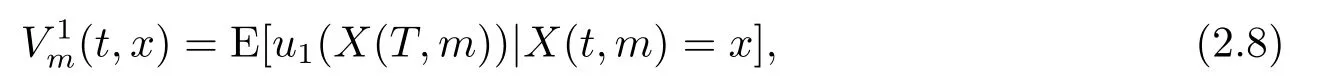
若保險公司不購買停止損失再保險,則保險公司在終端時刻T的期望盈余效用為

假設再保險公司也以期望盈余效用增加作為承保的依據,以再保險公司的安全系數η作為再保險價格.如果再保險公司接受保險公司的停止損失再保險策略,再保險公司在終端時刻T的期望盈余效用定義為

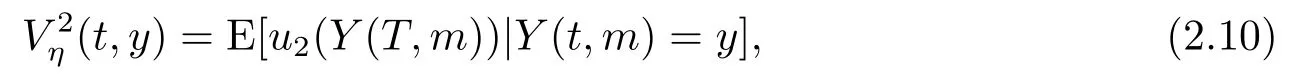
若再保險公司能夠決定承保的停止損失再保險數量,再保險公司承保停止損失再保險策略為m時在終端時刻T的期望盈余效用定義為

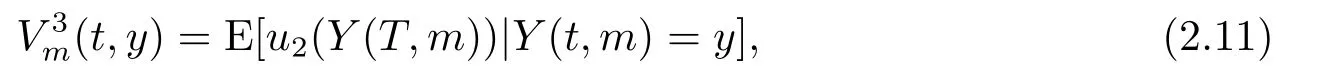
若再保險公司不接受保險公司的再保險,則再保險公司在終端時刻T的期望盈余效用為

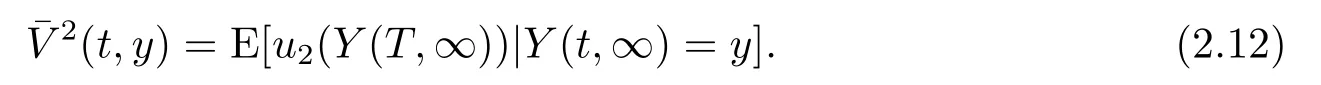
在實際再保險市場,保險公司可以選擇是否購買再保險及其數量,同時,再保險公司也可以選擇是否承保及其承保的價格和數量.因此,在保險公司和再保險公司之間存在著一個再保險策略博弈.一個合理的再保險合約應該同時考慮保險公司和再保險公司的利益,對雙方來說都是有利的,再保險合約才能成交.考慮到保險公司和再保險公司之間所處主導地位的不同,再保險策略選擇存在如下三種博弈情形:

(i)保險公司占主導.保險公司決定再保費和購買停止損失再保險數量,再保險公司只能根據再保費決定是否承保此數量再保險.保險公司選擇的最優停止損失再保險策略m?,使得

再保險公司決定承保時,再保費應該滿足下面條件

(ii)保險公司和再保險公司共同主導.保險公司決定購買停止損失再保險數量,再保險公司決定承保的再保費.此時,保險公司選擇最優停止損失再保險策略,使得

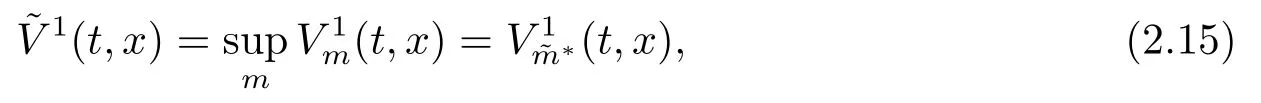
再保險公司選擇最優的再保費η?,使得

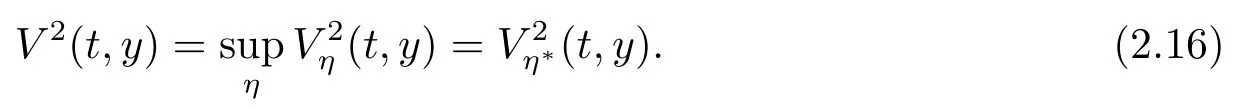
(iii)再保險公司占主導.再保險公司決定再保費和承保的再保險數量,保險公司只能根據再保費決定是否購買此數量再保險.此時,再保險公司選擇最優承保數量,使得

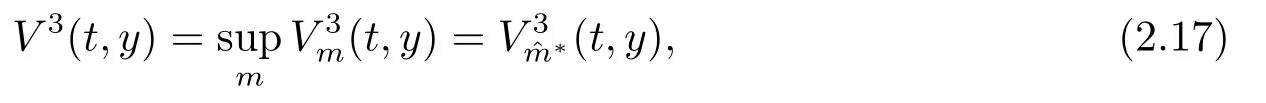
保險公司決定購買此數量的停止損失再保險時,再保費應該滿足下面條件

如果保險公司和再保險公司具有一般的效用函數,要判斷三種博弈情形下解的存在唯一性是比較困難的,即便三種博弈情形下存在解,要得到其解的顯示表達式也是十分困難的.

3.CARA效用保險公司和再保險公司

假設保險公司和再保險公司都具有指數效用函數,即

其中αi >0為常數絕對風險厭惡(constant absolute risk aversion(CARA))系數.此時,保險公司和再保險公司的絕對風險厭惡系數分別為α1和α2.

若保險公司不購買停止損失再保險,則由(2.4),(2.9)和(3.1)可得保險公司在終端時刻T的期望盈余效用為

若再保險公司不接受保險公司的停止損失再保險,則由(2.5),(2.12)和(3.1)可得再保險公司在終端時刻T的期望盈余效用為

Ⅰ 保險公司占主導

下面,在保險公司占主導下,考慮保險公司的最優停止損失再保險策略以及再保險公司決定承保的條件.

定理3.1保險公司的最優停止損失再保險策略為

相應的值函數為

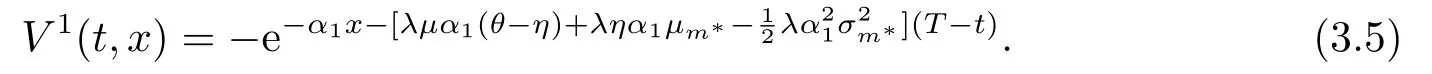
證根據動態規劃原理可知,V1滿足下面的Hamilton-Jacobi-Bellman(HJB)方程

其邊界條件為

為了求解(3.6),根據邊界條件(3.7),假設方程(3.6)具有如下形式的解

其中h(t)是一個待定函數,使得(3.8)是方程(3.6)的解,且由邊界條件(3.7)知h(T)= 1.因此,由(3.8)有

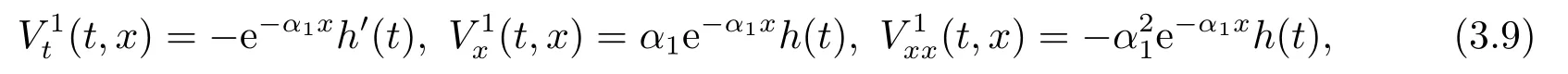
把(3.9)代入(3.6)化簡,可得

由一階最優化條件得到保險公司的最優停止損失再保險策略為

把m?=η/α1代入(3.10),化簡得

由邊界條件h(T)=1,可得

注3.1由定理3.1可知,保險公司的最優停止損失再保險策略僅僅依賴保險公司的絕對風險厭惡系數和再保費,獨立于索賠強度和每次賠付大小的分布.

定理3.2如果再保費η滿足

則再保險公司承保后能夠增加其效用,即有V2η(t,y)≥(t,y).

證由(2.5),(2.10)和(3.1)可知,再保險公司承保保險公司的停止損失再保險m?=η/α1后的期望終端盈余效用為

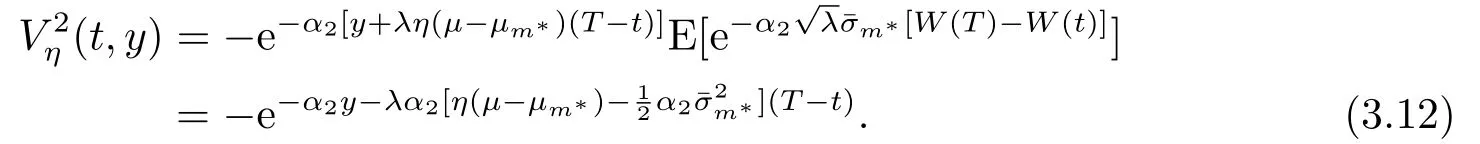
因此,由(3.3)可得

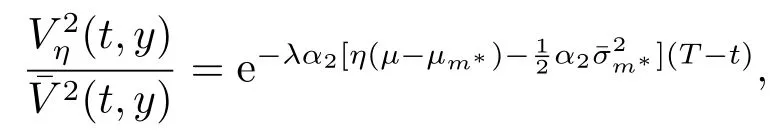
所以由λ>0和α2>0易知定理3.2成立.

推論3.1如果每次賠付額Zi服從參數為β的指數分布,則保險公司的的最優停止損失再保險策略為m?=η/α1,值函數為

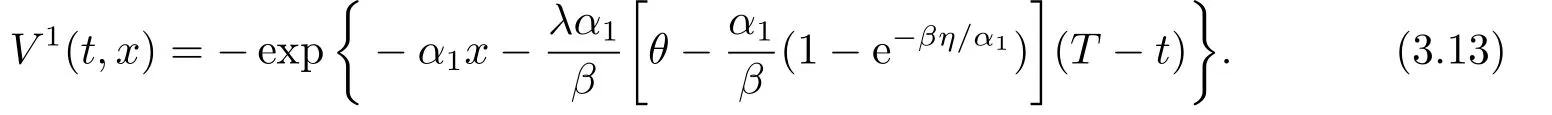
再保險公司承保后的值函數為

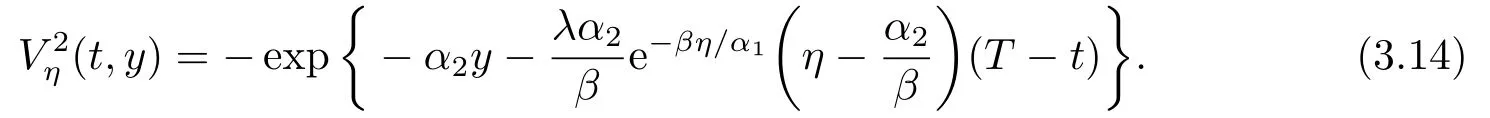
且當再保費時,有Vη2(t,y)(t,y).

證若索賠額Zi服從參數為β的指數分布,則有

和

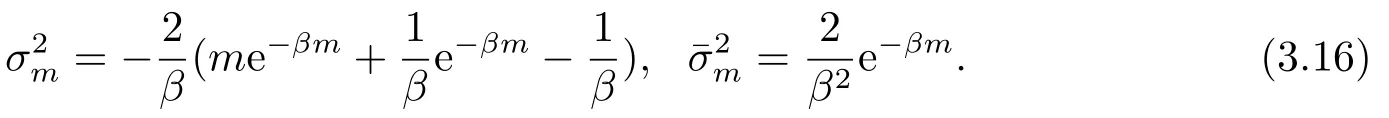
因此,把(3.15)和(3.16)分別代入(3.5)和(3.12)化簡可得(3.13)和(3.14).把(3.15)和(3.16)代入(3.11)化簡可得

Ⅱ 保險公司和再保險公司共同主導

下面,在保險公司和再保險公司共同主導下,考慮保險公司的最優停止損失再保險策略和再保險公司的最優再保費.

定理3.3保險公司的最優停止損失再保險策略為

再保險公司的最優再保費η?滿足下面的方程

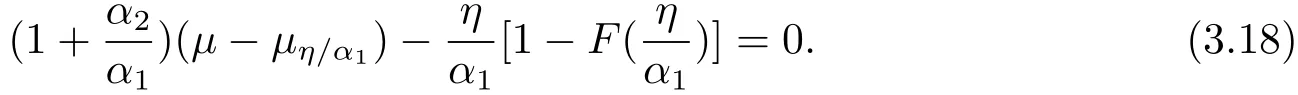
此時,保險公司的值函數為

再保險公司的值函數為

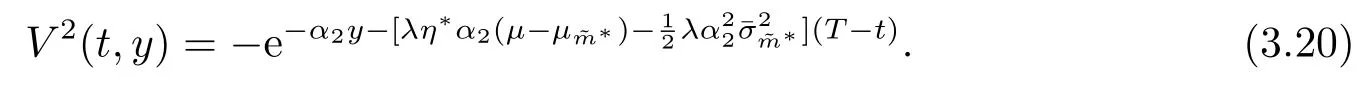
證由定理3.1可得,保險公司的最優停止損失再保險策略為m?=η/α1.把m?=η/α1代入(2.5),根據動態規劃原理可知,V2滿足下面的HJB方程

其邊界條件為

為了求解(3.21),根據邊界條件(3.22),假設方程(3.21)具有如下形式的解

其中g(t)是一個待定函數,使得(3.23)是方程(3.21)的解,且由邊界條件(3.22)知g(T)=1.因此,由(3.23)有

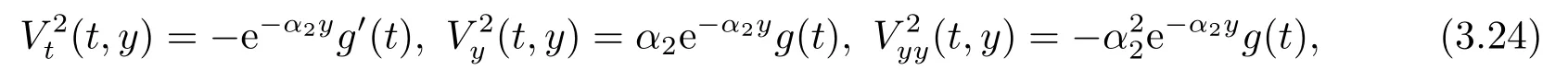
把(3.24)代入(3.21)化簡,可得

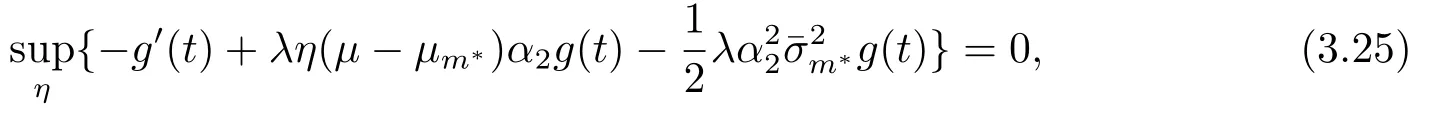
由一階最優化條件得到再保險公司的最優再保費η?滿足

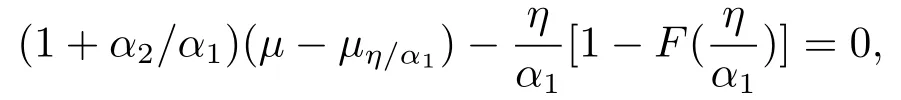
把m?和η?代入(3.25),化簡得

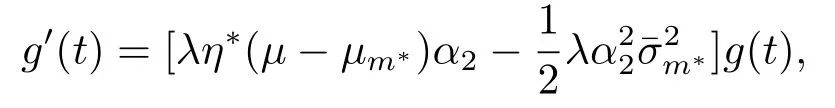
由邊界條件g(T)=1,可得

注3.2首先由(3.18)得到再保險公司的最優再保費,然后代入(3.17)得到保險公司的最優停止損失再保險策略.

推論3.2如果每次賠付額Zi服從參數為β的指數分布,則保險公司的的最優停止損失再保險策略為

值函數為

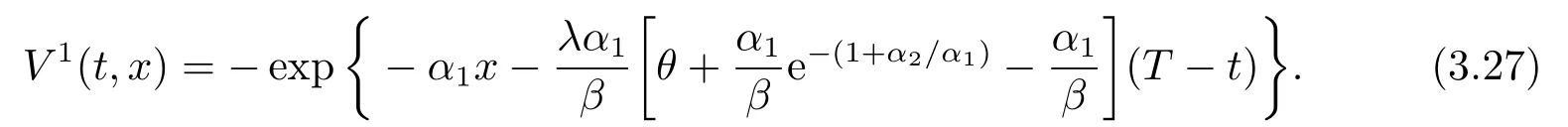
再保險公司的最優再保費為

值函數為

證若索賠額Zi服從參數為β的指數分布,則有(3.15)和(3.16)成立.因此,把(3.15)和(3.16)代入(3.18)化簡可得

Ⅲ 再保險公司占主導

下面,在再保險公司占主導下,考慮再保險公司的最優承保停止損失再保險策略以及保險公司決定購買該再保險時再保費滿足的條件.

定理3.4再保險公司的最優承保停止損失再保險策略滿足下面方程

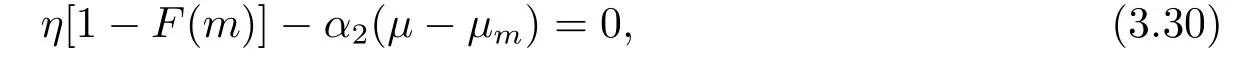
相應的值函數為

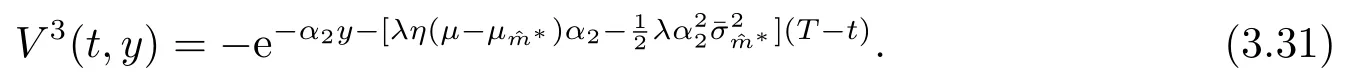
證根據動態規劃原理可知,V3滿足下面的HJB方程

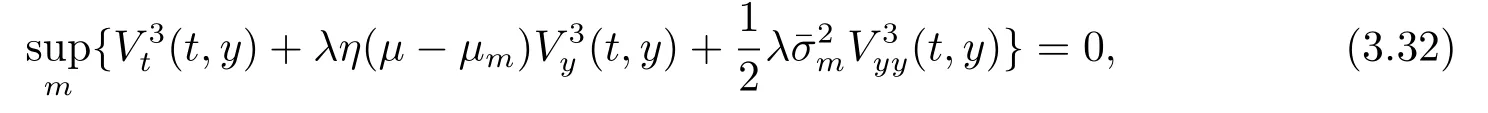
其邊界條件為

為了求解(3.32),根據邊界條件(3.33),假設方程(3.32)具有如下形式的解

其中f(t)是一個待定函數,使得(3.34)是方程(3.32)的解,且由邊界條件(3.33)知f(T)=1.因此,由(3.34)有

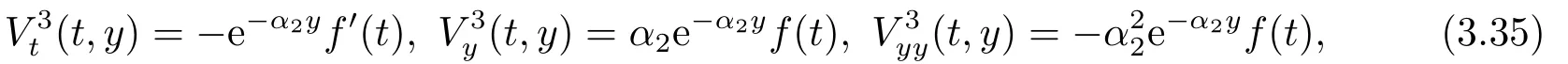
把(3.35)代入(3.32)化簡,可得

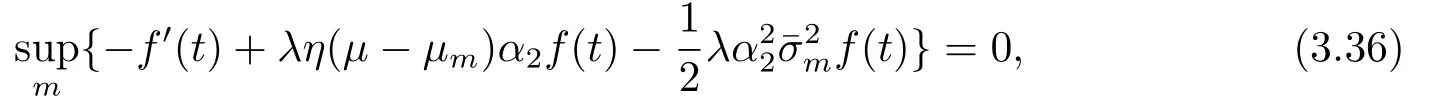
由一階最優化條件可得再保險公司的最優承保停止損失再保險策略滿足下面方程

由邊界條件f(T)=1,可得

注3.3由定理3.4可知,再保險公司的最優承保停止損失再保險策略不僅依賴再保險公司的絕對風險厭惡系數和再保費,而且還依賴每次賠付大小的分布.

定理3.5如果再保費η滿足

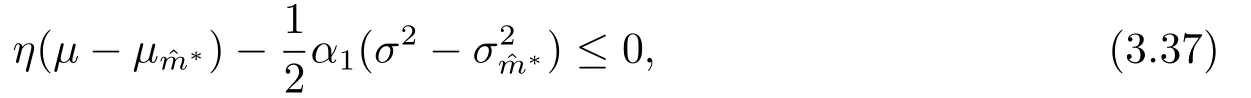
證由(2.4),(2.8)和(3.1)可知,保險公司購買停止損失再保險后在終端時刻T的期望盈余效用為

因此,由(3.2)可得

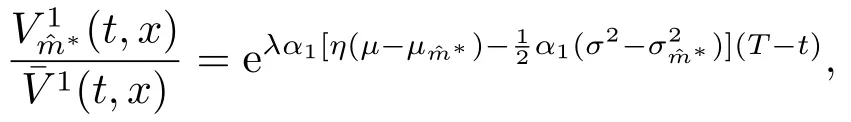
所以由λ>0和α1>0易知定理3.5成立.

推論3.3假設每次賠付額Zi服從參數為β的指數分布,則有

(i)如果η=α2/β,則再保險公司的最優承保停止損失再保險策略為任意非負常數,值函數為

(ii)如果ηα2/β,則再保險公司的最優承保停止損失再保險策略=∞,即再保險公司不愿承保任何數量的停止損失再保險,值函數為

保險公司不購買停止損失再保險,值函數為

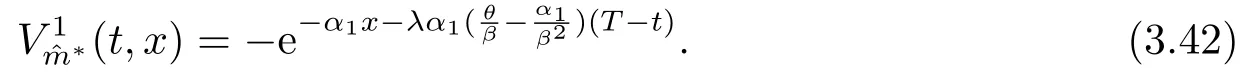
證如果索賠額Zi服從參數為β的指數分布,則(3.15)和(3.16)成立.因此,把(3.15)和(3.16)代入(3.30)化簡可得滿足下面方程

所以,當η=α2/β時,方程(3.43)的解為任意非負常數.把(3.15)、(3.16)、η=α2/β和分別代入(3.31)和(3.38)化簡可得(3.39)和(3.40).當ηα2/β時,方程(3.43)的解=∞,即再保險公司不承保任何停止損失再保險.因此,再保險公司和保險公司的值函數分保為(3.41)和(3.42).

注3.4由推論3.3可知,當時,任意非負常數的停止損失再保險合約都是可以成交的.此時,雖然承保后再保險公司的效用保持不變,但是由于有再保費收入,承保后再保險公司的規模會變大.

4.結果比較與靈敏性分析

下面在賠付額服從指數分布下分別考慮三種博弈情況下最優再保險合約與模型主要參數之間的關系,并通過數值計算得到保險公司和再保險公司的效用損益與模型主要參數之間的關系.除非特別說明,各模型參數取值如表4.1所示,其大小與實際較為一致.

表4.1 數值例子中的各個模型參數值

由于V1(t,x)<0和(t,x)<0,定義

為保險公司購買停止損失再保險后對應的效用損益.若L1(T)>0,則表示保險公司購買再保險后期望終端盈余效用會增加,即保險公司有效用收益,L1(T)的大小為保險公司效用增加的百分比;L1(T)<0表示保險公司購買再保險后期望終端盈余效用會減少,即保險公司有效用損失,L1(T)的大小為保險公司效用損失的百分比.同樣的,定義為再保險公司承保后對應的效用損益.若L2(T)>0,則表示再保險公司承保后有效用收益;若L2(T)<0,則表示再保險公司承保后有效用損失.

Ⅰ 保險公司占主導

由推論3.1容易得到下面的推論.

推論4.1(i)保險公司的最優停止損失再保險策略m?是α1的減函數,是η的增函數;

(ii)再保險公司愿意承保的最小再保費隨著再保險公司的絕對風險厭惡系數的增加而增加,隨著平均賠付額的增加而增加.

由推論4.1(i)可知,保險公司的最優自留停止損失是α1的減函數.因為α1為保險公司的絕對風險厭惡系數,α1越大,保險公司越厭惡風險,因此保險公司會自留更少的風險.同時,保險公司的最優自留停止損失是η的增函數.由于η為再保險公司的安全系數,η越大,購買再保險的成本越高,所以保險公司購買更少的再保險.這些結果都與實際相符合.由推論4.1(ii)可知,再保險公司愿意承保的最小再保費是α2的增函數.因為α2為再保險公司的絕對風險厭惡系數,α2越大,再保險公司越厭惡風險,因此再保險公司承保需要更高的再保費.同時,再保險公司愿意承保的最小再保費是β的減函數.這是因為β越大,賠付額的平均值越小,再保險公司承保面臨的風險越小,所以再保費越少.

由推論3.1,(4.1)和(4.2)可得保險公司的效用損益為

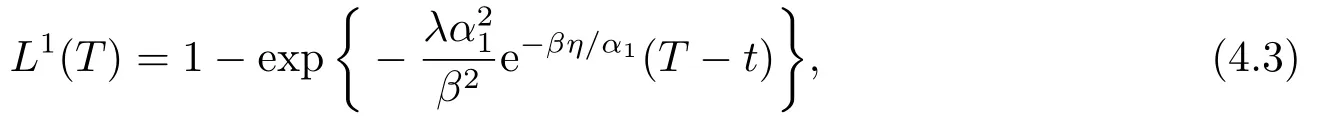
再保險公司的效用損益為

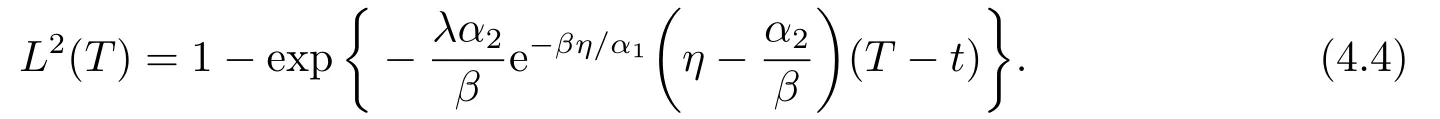
由(4.3)可知,保險公司購買停止損失再保險后有效用收益.當時,再保險公司承保后也有效用收益.此時,停止損失再保險合約可以成交.

推論4.2在保險公司占主導下,保險公司和再保險公司的效用收益與模型主要參數之間的關系如表4.2所示.

表4.2 效用收益Li(T)與模型主要參數之間的關系

證由(4.3)和(4.4)分別對相應的參數求導,化簡容易得到推論4.2的結論.下面僅僅給出L2(T)與η之間關系的證明,其它類似.根據(4.4),L2(T)對η求導,化簡得

圖4.1給出了保險公司和再保險公司的效用損益與再保費η之間的關系.由圖4.1可知,保險公司和再保險公司都有效用收益,即在此再保費下,保險公司購買停止損失再保險和再保險公司承保都能提高其效用,再保險合約可以成交.保險公司的效用收益L1(T)隨著再保費η的增加而減少,因為η越大,再保險成本越高,購買再保險需要花費更多財富,導致保險公司的期望盈余效用減少.再保險公司的效用收益L2(T)是再保費η的先增后減函數,這與直觀的再保費越高,再保險公司承保收取更多的保費,再保險公司具有更多的財富,從而期望盈余效用越大不一致.這是因為一方面,再保費越高,再保險公司承保收取更多的保費導致再保險公司期望盈余增加;另一方面,再保費越高,再保險成本越高,由推論4.1可知,保險公司購買更少的再保險導致再保險公司盈余減少.當再保費較小時,第一方面占主導,因此再保險公司的效用收益隨著再保費的增加而增加;當再保費較大時,第二方面占主導,因此再保險公司的效用收益隨著再保費的增加而減小.這些結果與表4.2所得結果一致.

圖4.1 效用損益與η之間的關系

圖4.2給出了保險公司和再保險公司的效用損益與每次賠付額分布參數β之間的關系.由圖4.2可知,保險公司的效用收益L1(T)隨著β的增加而減少,因為β越大,平均賠付額越小,由于保險公司是根據期望值保費原理收取保費,故保費減少且保險公司的分保保持不變,所以保險公司的期望盈余效用減少.再保險公司的效用收益L2(T)是β的先增后減函數.因為一方面,β越大,再保險公司承保后的賠付風險減小導致再保險公司期望盈余增加;另一方面,β越大,再保險公司是根據期望值保費原理收取再保費,再保費減少,導致再保險公司盈余減少.當β較小時,第一方面占主導,因此再保險公司的效用收益隨著β的增加而增加;當β較大時,第二方面占主導,因此再保險公司的效用收益隨著β的增加而減小.

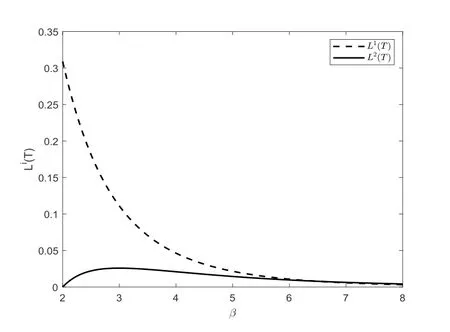
圖4.2 效用損益與β之間的關系

Ⅱ 保險公司和再保險公司共同主導

由推論3.2容易得到下面的推論.

推論4.3(i)保險公司的最優自留停止損失是保險公司絕對風險厭惡系數α1的減函數,是再保險公司絕對風險厭惡系數α2的增函數,是平均賠付額1/β的增函數;

(ii)再保險公司承保的最優再保費隨著再保險公司或再保險公司的絕對風險厭惡系數的增加而增加,隨著平均賠付額的增加而增加.

由推論4.3(i)可知,保險公司的最優自留停止損失是再保險公司絕對風險厭惡系數α2的增函數.因為α2為再保險公司的絕對風險厭惡系數,α2越大,再保險公司越厭惡風險,所以再保險公司承保需要更多的再保費,保險公司購買停止損失再保險成本更高,因此保險公司會自留更多的風險.同時,保險公司的最優自留停止損失是平均賠付額1/β的增函數.這是因為一方面1/β越大,賠付額的均值越大,保險公司需要購買更多的再保險;另一方面,1/β越大,由(3.28)知再保險公司承保的再保費越高,保險公司會減少再保險的購買.由于第二方面占主導,所以保險公司會自留更多的風險.保險公司的最優自留停止損失與α1之間關系的原因類似推論4.1解釋.由推論4.3(ii)還可以發現,再保險公司愿意承保的最優再保費是α1的增函數.因為α1為保險公司的絕對風險厭惡系數,α1越大,保險公司越厭惡風險,因此保險公司購買再保險愿意支付更高的再保費.再保險公司承保的最優再保費與α2和β之間關系的原因類似推論4.1的解釋.

由推論3.2,(4.1)和(4.2)可得保險公司的效用損益為

再保險公司的效用損益為

推論4.4在保險公司和再保險公司共同主導下,保險公司和再保險公司的效用收益與模型主要參數之間的關系如表4.3所示.

表4.3 效用收益(T)與模型主要參數之間的關系

表4.3 效用收益(T)與模型主要參數之間的關系

?ˉL1(T)?ˉL1(T)?ˉL1(T)?ˉL2(T)?ˉL2(T)?ˉL2(T)?α1?β?α2?α1?β?α2 0<α2 ≤α1 α2 >α1+ - - + - + -

證由(4.5)和(4.6)分別對相應的參數求導,化簡容易得到推論4.4的結論.

圖4.3給出了保險公司和再保險公司的效用損益與保險公司的絕對風險厭惡系數α1之間的關系.由圖4.3可知,保險公司和再保險公司的效用收益都隨著α1的增加而增加,保險公司和再保險公司都有效用收益,再保險合約是可以成交的.所得結果與表4.3所得結果一致.

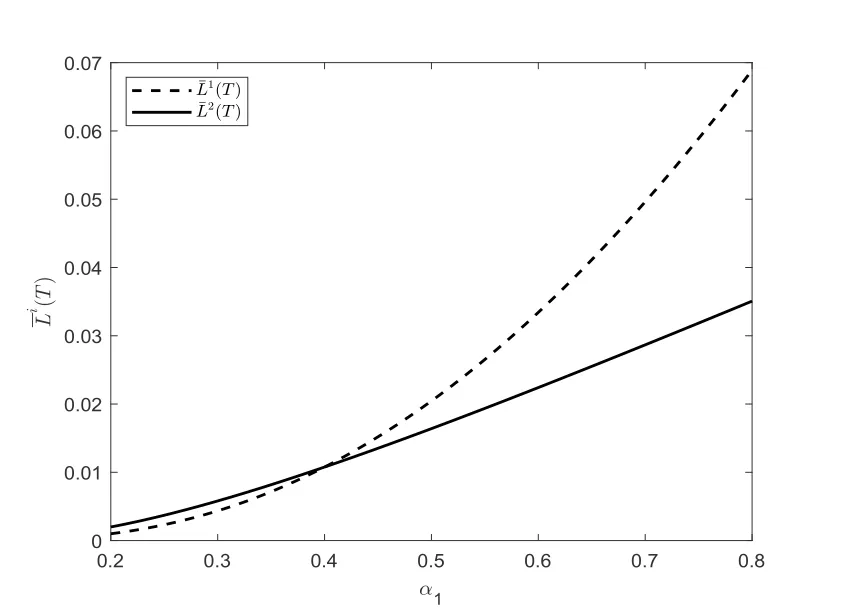
圖4.3 效用損益與α1之間的關系

圖4.4給出了保險公司和再保險公司的效用損益與再保險公司的絕對風險厭惡系數α2之間的關系.由圖4.4可知,保險公司的效用收益隨著α2的增加而減小.由推論4.3可知,再保費和保險公司的最優自留風險都是α2的增函數.因此,隨著再保險公司絕對風險厭惡系數的增加,保險公司自留風險增加,并且再保險公司承保收取更多的再保費,所以保險公司的期望盈余效用減小.從圖4.4可以發現,再保險公司的效用收益是α2的先增后減函數.因為一方面,α2越大,由推論4.3可知再保險公司承保收取更多的再保費,導致再保險公司期望盈余增加;另一方面,α2越大,由推論4.3可知保險公司購買更少的停止損失再保險,再保費減少導致再保險公司期望盈余減少.當α2較小時,第一方面占主導,因此再保險公司的效用收益隨著α2的增加而增加;當α2較大時,第二方面占主導,所以再保險公司的效用收益隨著α2的增加而減小.

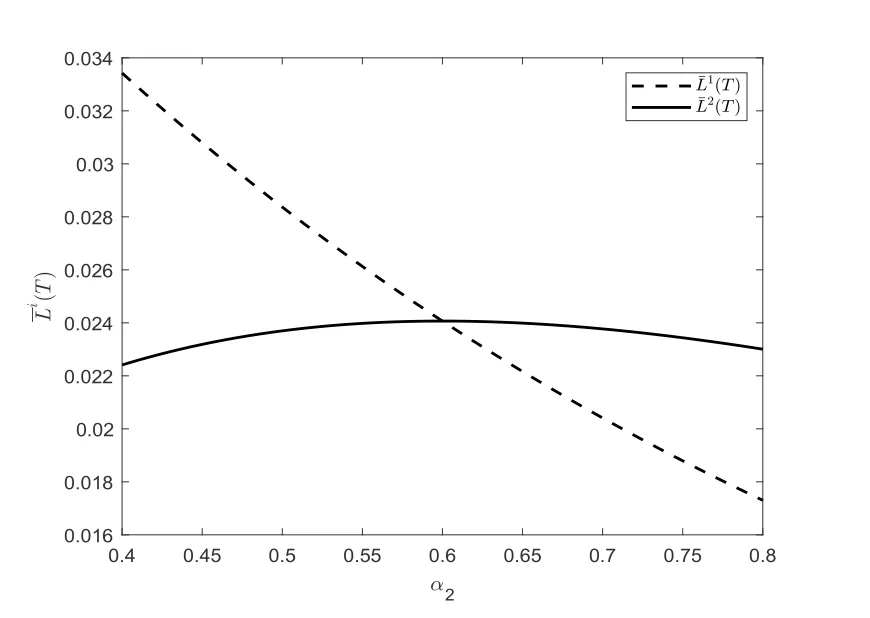
圖4.4 效用損益與α2之間的關系

Ⅲ 再保險公司占主導

由推論3.3容易得到下面的推論.

推論4.5(i)若η=α2/β,則再保險公司的最優承保停止損失再保險策略為任意非負常數,不隨任何模型參數的變化而變化;

(ii)若η=α2/β,則保險公司購買再保險愿意支付的最大保費隨著保險公司絕對風險厭惡系數的增加而增加,隨著平均賠付額的增加而增加.

如果η=α2/β,由(3.41)可知,再保險公司承保停止損失再保險策略為任意非負常數,再保險公司承保和不承保對應的期望終端盈余效用都一樣,所以再保險公司的最優承保停止損失再保險策略不隨任何模型參數的變化而變化.保險公司購買再保險愿意支付的最大保費與α1和β之間關系的原因類似推論4.3的解釋.

由推論3.3,(4.1)和(4.2)可得保險公司的效用損益為

再保險公司的效用損益為

推論4.6在再保險公司主導下,保險公司的效用收益與模型主要參數之間的關系如表4.4所示.

表4.4 效用收益(T)與模型主要參數之間的關系

表4.4 效用收益(T)與模型主要參數之間的關系

?

證由(4.7)分別對相應的參數求導,化簡容易得到推論4.6的結論.

由表4.4可知,保險公司的效用收益是再保險公司的最優承保停止損失再保險策略的先增后減函數.由于再保費η=α2/β是固定的,一方面,越大,保險公司購買更少的再保險,再保費減少導致保險公司期望盈余增加;另一方面,越大,保險公司自留更多的風險,面臨更大的賠付風險導致保險公司的期望盈余減少.當較小時,第一方面占主導,因此保險公司的效用收益隨著的增加而增加;當較大時,第二方面占主導,所以保險公司的效用收益隨著的增加而減小.