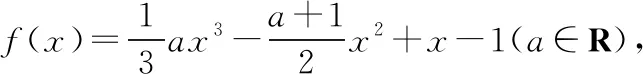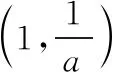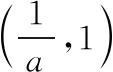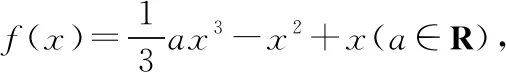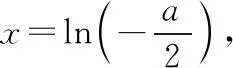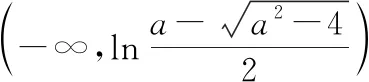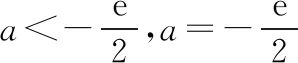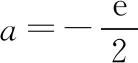含參函數單調性的討論

安徽 徐 雙

在高三的教學過程中，筆者發現很多學生對于函數單調性的討論，尤其是含參函數單調性的討論感到困惑，不知道從哪里開始討論，或者討論不全面.筆者結合自己在教學中的感悟，對含參函數單調性的常見問題進行了歸納總結.

原函數的單調性取決于導函數值的正負，所以，原函數單調性的討論本質上就是在定義域內討論導函數f′(x)>0或f′(x)<0的問題，即不等式問題.而不等式與函數一脈相承，導函數的零點是導函數值正負的臨界值，所以我們要研究導函數的零點，即方程f′(x)=0的根，一般會出現定義域內無根、一根、兩根的情況，超過兩根的情況不常見，在這里不再論述.下面筆者將從方程f′(x)=0為單根和雙根兩種情況進行論述，雙根型又分為二次函數(可因式分解)型、二次函數(不可因式分解)型、指數雙根型和混合雙根型四種情況，具體又從方程f′(x)=0是否有根、根是否在定義域內、若有兩根，兩根的大小等三個方面分別進行闡述.

一、單根型

所謂單根型，即方程f′(x)=0只有單根的情況，這種情況我們只需討論方程f′(x)=0是否有根，如果定義域有限制，還要進一步討論這個根是否在定義域內.

例1.已知函數f(x)=ex-ax(a∈R).

(1)若x∈R，討論函數f(x)的單調性；

(2)若x∈[0,1]，討論函數f(x)的單調性.

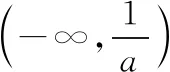
分析：第(1)問定義域沒有特殊限制，我們只需要考慮f(x)的導函數f′(x)=ex-a是否有零點.先假設它有零點，解f′(x)=0得x=lna，它有意義時需要a>0，也就是說a>0時導函數有零點x=lna，進而原函數的單調性就會在x=lna左右端發生變化，反之a≤0時，導函數f′(x)無零點，連續函數在定義域內無零點，說明它的函數值符號不變，即恒正或者恒負.那么我們得到，當a>0時，f(x)在(-∞,lna)上單調遞減，在(lna,+∞)上單調遞增；當a≤0時，f(x)在(-∞,+∞)上單調遞增.

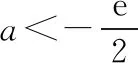
第(2)問有定義域的限制，我們令導函數的零點x=lna在(0,1)內，解得1

從上面例1的分析過程可以看出，我們討論的標準分別為導函數是否有變號零點以及變號零點是否在定義域內，抓住影響原函數單調性的最關鍵因素——導函數的零點，就能找到所要討論的參數臨界值，讓問題得以解決.

二、雙根型

方程f′(x)=0有兩個根的情況較復雜，根據決定導函數值符號的式子的形式，我們進一步分為二次函數(可因式分解)型、二次函數(不可因式分解)型、指數雙根型和混合雙根型四種情況，下面依次論述.

1.二次函數(可因式分解)型

這種情況我們要考慮方程f′(x)=0是否有根，根是否在定義域內以及兩根的大小，二次項系數若含參數，也要對它進行討論，這里面說到的幾種情況可能會出現一個或者多個，需要根據實際情況進行討論.

分析：方程f′(x)=ax2-(a+1)x+1=(ax-1)(x-1)，本題中定義域沒有特殊限制，需要從三個方面進行討論：方程f′(x)=0是否有根、二次項系數以及兩根大小.由前兩個方面可以把a分為a<0,a=0和a>0三種情況，根據兩根大小又可以把a>0進一步分為01三種情況，這樣我們就把參數a分為a<0,a=0,01五種情況.討論結果如下：

②當a=0時，f(x)在(1,+∞)上單調遞減，在(-∞,1)上單調遞增；

④當a=1時，f(x)在(-∞,+∞)上單調遞增；

2.二次函數(不可因式分解)型

當不能利用因式分解來求方程f′(x)=0的根時，我們要對判別式進行討論，來判斷導函數是否有變號零點，并用求根公式把零點表示出來，若二次項系數含參數還要對它進行討論，因為它會影響多項式的次數以及二次函數的開口方向，進而影響到原函數的單調性，若定義域有限制，還要討論導函數的零點是否在定義域內，至于它們的大小及正負，則可由二次項系數及韋達定理來判斷，不需要單獨進行討論.

分析：f′(x)=ax2-2x+1，因為二次項系數含參數，所以要把a分成a<0,a=0和a>0三種情況，再根據判別式Δ=4-4a來確定方程f′(x)=0是否有根，因此，最終把a分成a<0,a=0,0

①當a≥1時，Δ=4-4a≤0,f′(x)≥0恒成立，f(x)在(-∞,+∞)上單調遞增；

如果原函數有定義域的限制，可以根據一元二次方程根與系數的關系，結合判別式與韋達定理來討論方程f′(x)=0的根是否在定義域內，也可以解出方程f′(x)=0的根后，令它在定義域內去解出參數的范圍，進一步對參數進行分類討論，讀者可嘗試解下面的變式.

3.指數雙根型

指數雙根型的導函數的形式為f′(x)=ae2x+bex+c(a≠0)，可類比二次函數型，分為可因式分解和不可因式分解兩種，也可換元后利用復合函數的單調性進行討論.下面結合2017年全國卷Ⅰ文科第21題來進行說明.

例4.(2017·全國卷Ⅰ文·21節選)已知函數f(x)=ex(ex-a)-a2x，討論f(x)的單調性.

分析：f′(x)=2e2x-aex-a2=(2ex+a)(ex-a)，首先要看方程(2ex+a)(ex-a)=0是否有根，因為ex>0，

所以當a>0時，f′(x)=0有一根x=lna，所以f(x)在(lna,+∞)上單調遞增，在(-∞,lna)上單調遞減；

當a=0時，方程f′(x)=2e2x>0恒成立，f(x)在(-∞,+∞)上單調遞增；

上面例4中的導函數對應表達式是可因式分解的，還有不可因式分解的，這時需要類比二次函數(不可因式分解)型來討論，必要時進行換元，利用復合函數的單調性進行討論，通過下面的例子來看看具體的做法.

例5.(2020·合肥三模文·21節選)已知函數f(x)=ex-e-x,g(x)=ax(e為自然對數的底數)，其中a∈R.試討論函數F(x)=f(x)-g(x)的單調性.

分析：F′(x)=ex+e-x-a，因為F′(x)=ex+e-x-a≥2-a，

所以，當a≤2時，F′(x)≥0恒成立，F(x)在(-∞,+∞)上單調遞增；

4.混合雙根型

混合雙根型是指導函數由一次因式與指數型因式或者對數型因式相乘構成的，這種情況可類比二次函數(可因式分解)型來進行討論，可能會涉及導函數是否有根、根是否在定義域內以及兩根大小問題，同時也要注意每個因式對應的函數的單調性，這會影響雙根型函數的“開口”方向.

例6.(2016·全國卷Ⅰ文·21節選)已知函數f(x)=(x-2)ex+a(x-1)2，討論f(x)的單調性.

①當a≥0時，f(x)在(1,+∞)上單調遞增，在(-∞,1)上單調遞減；

結束語

通過上面的題型分類及例題分析，筆者把高考中常見的含參函數單調性的討論進行了總結歸納.對于此類問題的教學，一定要讓學生理解單調性問題的解題關鍵是導函數在定義域內是否存在變號零點，導函數在定義域內存在變號零點，原函數在定義域內單調性就會發生改變，反之，連續的原函數的單調性就不會發生變化.至于導函數在定義域內是否存在零點，則需要學生掌握一次函數、二次函數、指數函數、對數函數和三角函數等函數零點的求解方法，有時還可能用到零點存在性定理，涉及猜根、卡根及“隱零點”問題，本文不再論述.在討論單調性時，可以借助一次函數和二次函數，向學生展示導函數值正負的示意圖，幫助學生理解函數增減的變化，以便更好地由圖象寫出正確的單調區間.