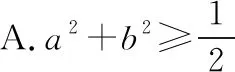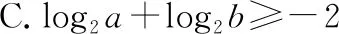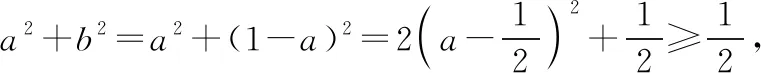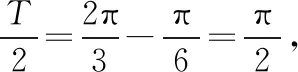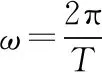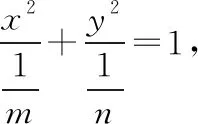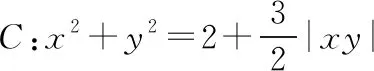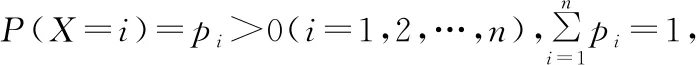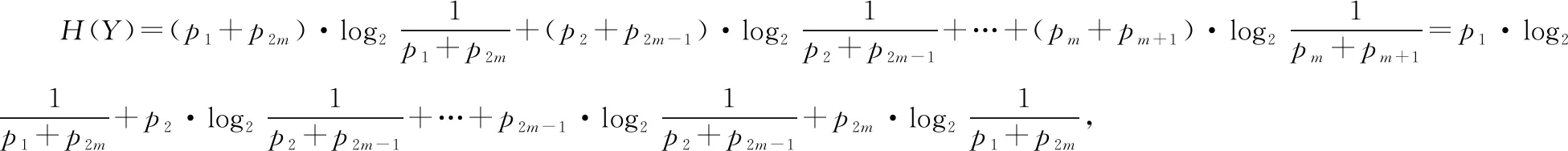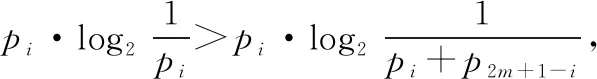例析高考新題型的命制與解答策略
——以2020年新高考Ⅰ卷(供山東省使用)多選題為例

江蘇 曾小娟

隨著《普通高中數學課程標準(2017年版2020年修訂)》的頒布，高考的改革也不斷深入.為了能更好地考查學生的數學素養，高考試卷的新題型也不斷涌現，比如2020年新高考Ⅰ卷(供山東省使用)中就出現了多項選擇題.多項選擇題，相對于單項選擇題而言，考查容量大、涉及知識點多、解題思路廣、數學思想豐富，又因多級得分模式能對考生多層次區分，所以多選題對能力的考查更加深入，要求學生具備完整、細致、全面的思維品質；多項選擇題出現在高考題中，可以增強數學考試的選拔功能，實現考試目標，但目前市面上模擬卷中出現的一些多項選擇題的命制很牽強，比如以下兩道試題：

(1)若圓(x-a)2+(y-a)2=1(a>0)上總存在點到原點的距離為3，則實數a的取值范圍不可能是

( )

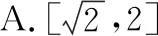
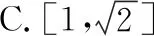
(2)下列說法正確的是

( )

A.直線x-y-2=0與兩坐標軸圍成的三角形的面積是2

B.點(0,2)關于直線y=x+1的對稱點為(1,1)

C.在△ABC中，若A

很顯然第一題就是對現有的單項選擇題直接進行否定而得到,而第二題就是把一些知識點湊在一起、把幾個不相關的真命題和假命題放在一起，類似拼盤式得到大雜燴型的試題.那么優秀的多選題究竟該如何命制呢？引起了筆者進一步思考.

多項選擇題應該是數學核心素養的集中展示，可以是基礎知識、基本技能、基本思想、基本活動經驗等四基的體現，也可以是發現問題、提出問題、分析問題、解決問題等四能的考查；可以直接考查學生的基礎知識、基本技能的掌握情況，也可以考查基本思想和基本活動經驗，測評學生分析問題和解決問題的能力，還可以設計新運算、新概念等新情境問題，測評學生發現問題和提出問題的能力.筆者認為多項選擇題的每一個選項之間應該具有知識的內在聯系或者思想方法的相通性.筆者通過研究2020年新高考Ⅰ卷(供山東省使用)的多項選擇題及北京、浙江、天津等高考卷中的多空型填空題，同時研究了歷年物理等學科高考試題多項選擇題的命制方式，基于主干知識、基本思想方法、學生素養等三個方向，結合2020年新高考Ⅰ卷(供山東省使用)談談多項選擇題的命制方式及相應的解題策略.

1.命制方式

1.1基于主干知識命制試題

高中階段，數學的主干知識主要有預備知識(集合、簡易邏輯、不等式等)、函數、幾何與代數、概率與統計、數學建模活動與數學探究活動等內容，基于主干知識命制多項選擇題就是基于以上幾塊主干知識點發散出多個選項進行命制，可以分為相同知識點的命制和不同知識點的命制.相同知識點的命制是基于主干知識命制多項選擇題最基本的方式，而不同知識點的命制需考慮其內在聯系，這種命制方式恰好體現了高考在知識點的交匯處命題的習慣，這種綜合性也恰好能考查考生的數學思維能力及靈活運用所學知識解決問題的能力.

【例1】(2020·新高考Ⅰ卷(供山東省使用)·11)已知a>0，b>0，且a+b=1，則

( )

評注：本題是基于不等式這塊的主干知識，結合了基本不等式、指數函數及對數函數的單調性，發散出多個選項進行命制，可以根據a+b=1，結合基本不等式及二次函數知識進行求解，主要考查不等式的性質，考查數學運算的核心素養.

命制題1：已知函數f(x)=2x，g(x)=2x-8，則下列結論正確的是

( ).

A.若h(x)=f(x)g(x)，則函數h(x)的最小值為16

B.若h(x)=f(x)|g(x)|，則函數h(x)的值域為R

C.若h(x)=|f(x)|-|g(x)|，則函數h(x)有且僅有一個零點

D.若h(x)=|f(x)|-|g(x)|，則|h(x)|≤16恒成立

評注：本題是筆者所在學校的一次周測試題，答案選BCD，是基于函數知識，以f(x)=2x，g(x)=2x-8為條件，涵蓋4個不同的函數的屬性(如定義域、值域、奇偶性、單調性、周期、零點等)，很好地考查了函數的性質，考查了學生數學運算、邏輯推理的核心素養.

1.2基于數學思想方法命制試題

數學基本思想方法主要有數形結合、化歸與轉化、分類討論、方程、建模、類比、歸納推理、極限等.基于思想方法命制試題就是基于以上重要的數學思想或解決一類問題的通性通法發散出多個選項進行命制，可以分為基于重要數學思想方法的命制和基于研究問題的一般方法的命制.基于重要的數學思想方法是基于數學思想方法命制多選題最基本的方式，而研究類似問題的相同的思想方法的命制，需考慮研究新問題與研究老問題之間思想方法的內在聯系，這種命制方式恰好體現了高考考查學生數學思維能力及靈活運用所學知識解決問題的能力.

【例2】(2020·新高考Ⅰ卷(供山東省使用)·10)如圖是函數y=sin(ωx+φ)的部分圖像，則sin(ωx+φ)=

( )

【例3】(2020·新高考Ⅰ卷(供山東省使用)·9)已知曲線C:mx2+ny2=1.

( )

A.若m>n>0，則C是橢圓，其焦點在y軸上

D.若m=0，n>0，則C是兩條直線

評注：本題考查研究曲線的一般方法及曲線方程的特征，側重考查數學運算的核心素養；熟知常見曲線方程的特點及其之間的區別是求解本題的關鍵，可以結合選項逐項分析進行求解.

( )

A.曲線C關于坐標原點對稱

B.曲線C恰好經過6個整點(即橫、縱坐標均為整數的點)

C.曲線C上任意一點到原點的距離的最小值為2

D.曲線C所圍成的區域的面積小于4

1.3基于數學素養命制試題

高中數學的解題首要任務是讓學生的解題能力得到培養，課標對培養學生能力的要求，由開始的“四基”到“四能”，演變到現在的“六大核心素養”；多項選擇題應該是數學六大核心素養的集中展示，不僅可以考查“四基”，更能很好地考查“四能”等，基于數學素養命制試題就是以開放性問題、探索性問題、新定義性問題出現，考查學生的數學六大核心素養.學生通過對此類問題的解決，學會用數學的眼光看客觀世界，用數學的思維思考現實世界，用數學的語言表達現實世界.

( )

A.若n=1，則H(X)=0

B.若n=2，則H(X)隨著p1的增大而增大

D.若n=2m，隨機變量Y所有可能的取值為1,2,…,m，且P(Y=j)=pj+p2m+1-j(j=1,2,…,m)，則H(X)≤H(Y)

解析：對于A選項，若n=1，則i=1,p1=1，所以H(X)=-(1×log21)=0，所以A選項正確.對于B選項，若n=2，則i=1,2，p2=1-p1，

所以H(X)=-[p1·log2p1+(1-p1)·log2(1-p1)]，

則H(X)隨著n的增大而增大，所以C選項正確.

對于D選項，若n=2m，隨機變量Y的所有可能的取值為1,2,…,m，且P(Y=j)=pj+p2m+1-j(j=1,2,…,m).

所以H(X)>H(Y)，所以D選項錯誤，故選AC.

點評：本題考查對新定義“信息熵”的理解和運用，考查學生分析、思考和解決問題的能力，涉及對數運算和對數函數及不等式的基本性質的運用，可以結合選項逐項分析進行求解，對于A選項，求得H(X)，由此判斷出A選項的正確性；對于B選項，利用特殊值法進行排除；對于C選項，計算出H(X)，利用對數函數的性質可判斷出C選項的正確性；對于D選項，計算出H(X),H(Y)，利用基本不等式和對數函數的性質判斷出D選項的正確性.

2.解答策略