基于NSGA-Ⅱ的冷源機房設備運行參數多目標優化
閆軍威, 盧澤東, 周 璇
(華南理工大學機械與汽車工程學院, 廣州 510640)
中央空調系統是建筑內部的耗能大戶,其能耗占比超過50%[1]。整個中央空調系統能耗來源主要由3部分組成:主機能耗、輸送能耗、末端能耗,其中末端能耗約占空調能耗的15%[2]。而中央空調冷源機房設備包含冷水主機、冷凍泵和冷卻泵,因此,冷源機房設備能耗占到中央空調系統總能耗一半以上。在實際工程中,高效運行的冷源機房一直是空調節能研究領域關注的重點,同時冷源機房運行參數優化也是研究人員和工程技術人員關注的熱點問題。
隨著對中央空調節能優化的深入研究,優化系統參數已經成為提高空調系統性能和空調節能量的有效手段。文獻[3]針對現有的熱舒適性控制方法存在的不足,采用復合形法求得滿足熱舒適條件下的空調能耗值最小時的最優組合參數,適用于夏熱冬冷地區辦公建筑空調系統的實時節能舒適控制。文獻[4]通過建立空調系統能耗模型,運用蟻群算法對總能耗最小進行尋優,經過運行測試后的結果表明,優化后的節能率平均達到22.3%。文獻[5]為實現風量水量最優組合優化,設定風機和冷凍泵的總能耗最小為目標函數,利用遺傳算法對模型求解,與常規運行策略相比,得到的優化設定值的節能率達到13.38%。文獻[6]為了提高汽車暖通空調系統(heating,ventilating and air conditioning,HVAC)系統的性能,通過遺傳算法選擇四通百葉窗式冷凝器進行多目標優化,以冷凝器的傳熱速率最大和冷凝器壓降最小為雙目標來優化冷凝器性能,結果表明,與初始冷凝器狀態相比,最佳冷凝器的傳熱速率提高4%,壓降降低8%。Nasruddin等[7]以表征熱舒適度的指標——不滿意百分比的預測數(predicted percentage of dissatisfied,PPD)和最小年度能耗為優化目標函數,利用人工神經網絡并結合多目標遺傳算法結合來優化HVAC系統,最后得到的優化效果明顯,為研究復雜的中央空調優化問題提供了參考;文獻[8]運用兩種多目標優化算法對中央空調系統進行優化,將能效比和制冷量設置為雙目標,并與單目標優化進行比較,得到不同的多目標優化方法在運算上各具優勢的結論,其中,MO-DNS-PSO算法的運行效率更高,DNS-PSO算法的收斂性更好。
現有的參數優化研究中,通常是將能耗或能效視為唯一目標函數來進行優化研究,但這種優化方式具有一定局限性。空調系統運行參數的多目標優化研究大多集中在汽車空調領域,現有的中央空調多目標優化研究尚缺少對系統運行性能的量化研究。中央空調冷源機房設備數量眾多,運行工況復雜且運行參數繁多,各參數之間耦合作用較強。在空調系統運行時,冷水主機運行參數和冷凍側、冷卻側的運行參數相互耦合,冷水機組處于較大制冷量運行時往往難以保證系統總能耗水平較低,因此,空調系統參數優化可作為復雜的多目標優化問題進行求解。
多目標優化算法現已成為求解復雜的多元非線性問題的必要方法。常用的多目標進化算法主要有粒子群算法、模擬退火算法、非支配排序算法、差分進化算法等。其中,非支配排序遺傳算法Ⅱ(non-dominated sorting genetic algorithm Ⅱ,NSGA-Ⅱ)具有較強的變量處理能力,能夠最大限度地保持各優化目標之間的獨立性和較好地全局尋優能力[9]。該算法由于具有運行速度快、解集收斂性好的優點,已經被廣泛應用于眾多研究領域。
針對上述問題,現提出一種基于NSGA-Ⅱ算法的冷源機房設備系統運行參數的多目標優化方法,以廣州某商場建筑的空調冷源機房系統為研究對象,驗證NSGA-Ⅱ算法在冷源設備系統運行參數優化的適用性和有效性。
1 方法及原理
1.1 多目標優化方法
所提出的多目標優化方法適用于空調冷源機房設備系統,流程框架如圖1所示,步驟如下。
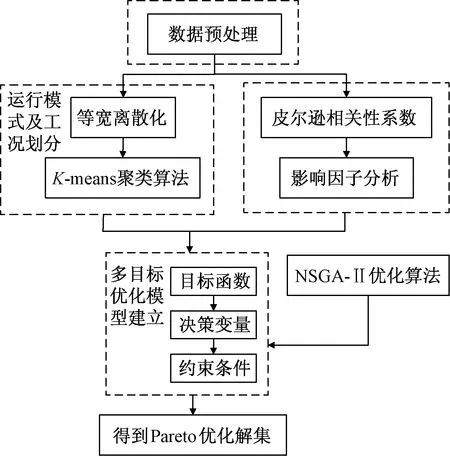
圖1 冷源機房設備系統的多目標優化框架Fig.1 Multi-objective optimization framework of cold source equipment room equipment system
步驟一數據預處理:對采集的空調系統大量歷史運行數據進行數據清洗,得到有效數據。
步驟二工況劃分:在數據預處理的基礎上,采用等寬離散化劃分運行模式,再利用K-means聚類算法劃分出運行工況。
步驟三影響因子分析:分析目標函數與影響因子間的相關性,進而確定決策變量。
步驟四多目標優化模型建立:確定模型的目標函數、決策變量以及約束條件,建立多目標優化數學模型。
步驟五利用NSGA-Ⅱ算法對模型實施優化,得到Pareto最優解集。
1.2 多目標優化問題
多目標優化問題是需要考慮多個目標滿足某種條件下的最優化問題,最早由法國經濟學家V. Pareto在1896年提出。隨后,眾多學者不斷地探究多目標優化問題,多目標優化已成為許多領域的重要研究方向。多目標優化問題通常可描述為
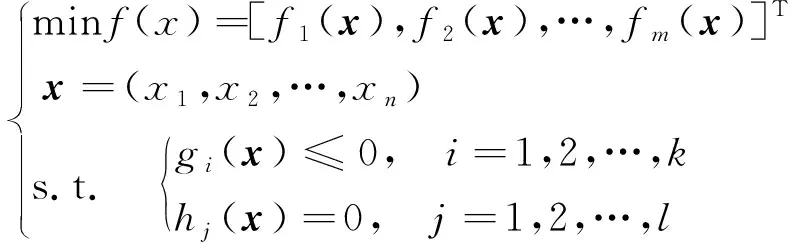
(1)
式(1)中:x為決策變量。
1.3 Pareto前沿
Pareto前沿指的是所有非支配解的集合。
非支配解指的是假設S1、S2是多目標優化中的兩個解,對于所有目標而言,若S1均優于S2,則稱S1支配S2;若S1的解沒有被其他解所支配,則S1稱為非支配解(Pareto解)。
針對多目標優化問題,最終期望得到Pareto前沿,當有兩個優化目標時,得到的Pareto前沿是一條曲線,兩個以上目標時的Pareto前沿是一個超曲面。Pareto前沿上的所有解均不受其之外的解所支配。因此,Pareto前沿可為多目標優化問題提供一系列較優的解點。
1.4 NSGA-Ⅱ算法
NSGA-Ⅱ算法采用非支配排序,可以快速得到種群分布均勻的非劣最優解,具有很強的穩定性和適應性[10]。最初,Srinivas 等[11]提出NSGA算法,需要在選擇算子執行之前對個體之間的支配關系進行分層,使得該算法計算復雜度較高且難以確定共享半徑。文獻[12-13]提出NSGA-Ⅱ算法,該算法引入了精英策略,應用快速非支配排序降低了復雜度,并且使用擁擠度比較算子,合并父代種群跟子代種群,使得下一代的種群從雙倍的空間中進行選取,保留了種群中的優秀個體。該算法較以往多目標優化算法在應用上更具有廣泛性和優越性。
為滿足制冷量與系統總能耗作為雙目標函數來優化系統運行參數,采用經典的多目標優化算法NSGA-Ⅱ尋求模型的最優解集,獲得各工況的最優運行參數,進而分析各工況下的能效優化情況。NSGA-Ⅱ多目標優化算法流程圖如圖2所示,具體步驟如下。
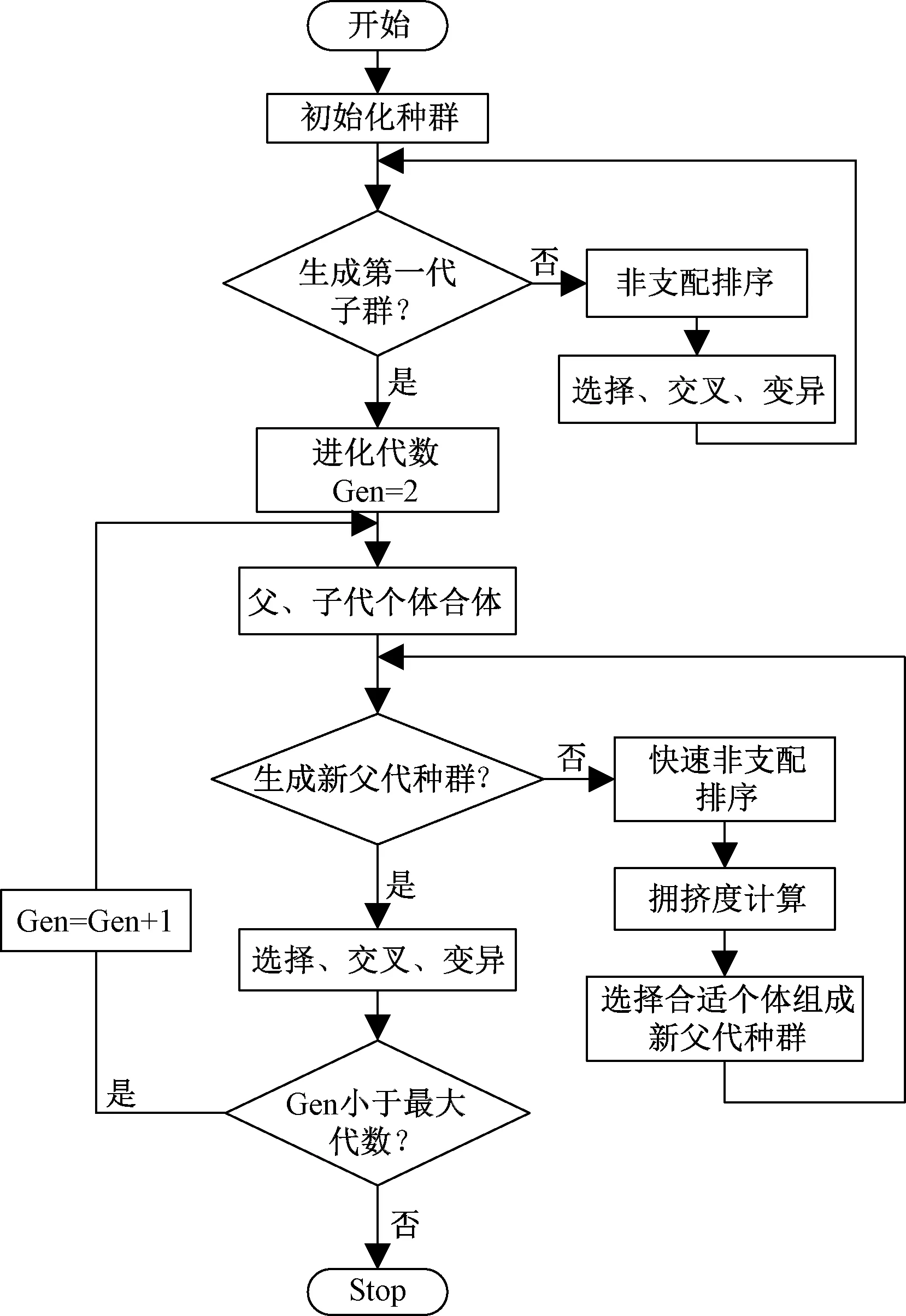
圖2 NSGA-Ⅱ多目標優化算法流程Fig.2 Multi-objective optimization algorithm of NSGA-Ⅱ
步驟一隨機產生規模為N的初始種群。
步驟三從第二代開始,將父代種群與子代種群合并,進行快速非支配排序。
步驟四對每個非支配層中的個體進行擁擠度計算,根據非支配關系以及個體的擁擠度選取合適的個體組成新的父代種群;
步驟五達到滿足程序結束的條件后,算法終止,否則,返回步驟二。
2 案例分析
2.1 研究對象
將廣州市某商場建筑的中央空調冷源機房系統作為研究對象,該系統包含4臺離心式冷水機組、6臺冷凍水泵和6臺冷卻水泵設備,具體參數如表1所示。該單位冷源機房安裝有自動控制系統及數據采集系統,采集冷源機房設備的運行參數存儲在數據庫中,包括冷凍水流量、冷凍水供回水溫度、冷凝出水壓力、冷凝回水壓力、冷卻水供回水溫度、冷卻水流量等,共計18維運行參數。

表1 制冷機房具體設備參數Table 1 Parameters of specific equipment in refrigeration equipment room
采用該商場2018年1—12月共計一年的歷史數據。根據實際現場運行情況得知,該商場在較多時間處于單臺主機運行狀態。為保證算法優化的有效性,僅考慮2臺小機單獨運行時的工況。經過數據統計分析,其運行數據量共計27 506條。
2.2 數據處理
2.2.1 數據預處理
數據處理是將數據能夠成功擬合模型和實施優化的重要前提,根據對數據的要求,需要對數據進行預處理。為擬合各工況模型,首先對原數據庫中數據進行屬性規約,最終得到制冷量、冷凍水流量、冷凍出水溫度、冷凍回水溫度、冷卻水流量、冷卻水出水溫度、冷卻回水溫度、主機功率、水泵功率及頻率共10維屬性參數。由于數據在傳輸過程中可能出現錯誤以及設備運行出現的可能故障,處于剛開關機階段的數據以及出現極限值數據屬于異常數據,應將其剔除;剔除缺失值和異常值后,在Python上采用拉依達準則對各項數據進行統計計算,剔除較大偏差數據;最終得到有效數據共計 17 380 條。數據預處理流程如圖3所示。
在這社會動蕩時期,陶淵明去踐行了他的“平生之志”,十三年間先后五次做官。十三年,不管他所任官職大小,還是幾仕幾處,都是他為實現“大濟蒼生”的理想抱負而不斷嘗試、不斷失望終至絕望的行動體現。所以,陶淵明并不是沒有出仕的志向,而是混亂的現實讓他沒有實現志向的機會,所以他最后一次為官,做了80多天的彭澤縣令,以“尋程氏妹喪于武昌,情在駿奔,自免去職”的理由,在序言中寫道:“嘗從人事,皆口腹自役。于是悵然慷慨,深愧平生之志。”在這樣的遺憾中結束了他的“兼濟天下”的“平生之志”,留下的是不能有所作為的深深的慚愧。所以,東晉這一動蕩的時代,造就了陶淵明的“平生之志”,也用現實毀滅了他的“平生之志”。

圖3 數據預處理流程Fig.3 Data preprocessing
2.3 影響因子分析
冷源機房設備系統能效受到負荷率、冷凍水流量、冷凍出水溫度、冷凍回水溫度、冷卻水流量、冷卻水回水溫度等影響,并且各參數間耦合性較強。為了研究各參數對系統能效的影響程度,在完成數據預處理的基礎上,分析系統能效與影響因素間相關性,以此為多目標模型中決策變量的選取依據。本研究選取適用于描述兩變量之間線性相關的皮爾遜(Pearson)相關系數,其定義是兩變量的協方差與標準差的比,公式表示為

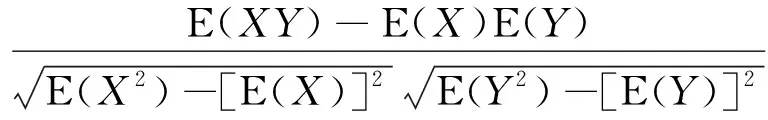
(2)
式(2)中:cov(X,Y)為隨機變量X與Y的協方差;σX與σY分別為X與Y的標準差;ρX,Y介于-1~1。
系統能效與影響因子間的Pearson相關系數如表2所示。可以看出,對冷源機房設備系統能效產生影響的因素從大到小依次是:負荷率、冷凍水流量、冷卻回水溫度、冷凍回水溫度、冷卻水流量、冷凍出水溫度和冷卻出水溫度。研究需要建立系統能耗和制冷量的雙目標數學模型,結合影響因子相關性系數分析結果,選取相關性系數較大的冷凍水流量、冷卻回水溫度、冷凍回水溫度、冷卻水流量和冷凍出水溫度共5個參數作為模型的決策變量,進而建立多目標優化的目標函數。

表2 系統能效與影響因子間的Pearson相關系數Table 2 Pearson correlation coefficient between energy efficiency and impact factor on air-conditioning system
2.4 運行模式及工況劃分
根據上述影響因子分析結果,在中央空調冷源機房系統中,負荷率是能直接反映系統運行狀態的重要指標。為充分反映中央空調冷源機房設備系統能效受到內外因素的影響,首先利用等寬離散化將負荷率劃為4個等寬區間運行模式,剔除在負荷率60%以下的不穩定工況數據;再利用K-means聚類算法在4種運行模式下對室外環境溫度和室外環境濕度兩個參數進行聚類分析。
K-means聚類算法是一種無監督的機器學習算法,它需選取k個初始聚類中心Ci(1≤i≤k),然后通過迭代計算原理得到樣本中各簇的相似度,其相似度是通過歐氏距離進行計算,數學表達式如式(3)。確定最佳聚類數目k是該算法的難點,采用樣本聚類誤差平方和(sum of squared error,SSE)來判定最佳k。在每次聚類后計算SSE,隨著聚類迭代,SSE會越來越小,最后會趨于穩定,變化過程的開始階段下降率很大,當下降率首次變緩時的k被看作最佳的聚類數目。SSE表達式如式(4)所示。
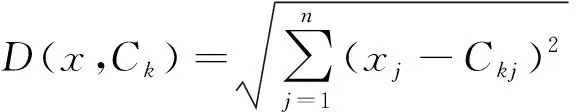
(3)
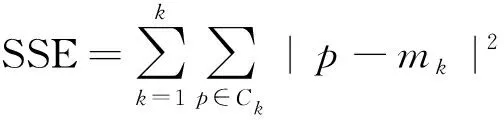
(4)
式中:x為數據對象;Ck為第k個聚類中心;n為數據對象尺寸;xj為x的第j個運行參數值;Ckj為Ck的第j個屬性值;p為各簇中的運行參數值;mk為第k個簇的中心。
根據通過K-means聚類和誤差平方和斷定方法對4種運行模式下的運行數據進行聚類劃分,從而得到系統的基本運行工況,運行模式及聚類劃分情況如表3所示。共劃分出32種基本運行工況,圖4是32種基本運行工況的具體情況。
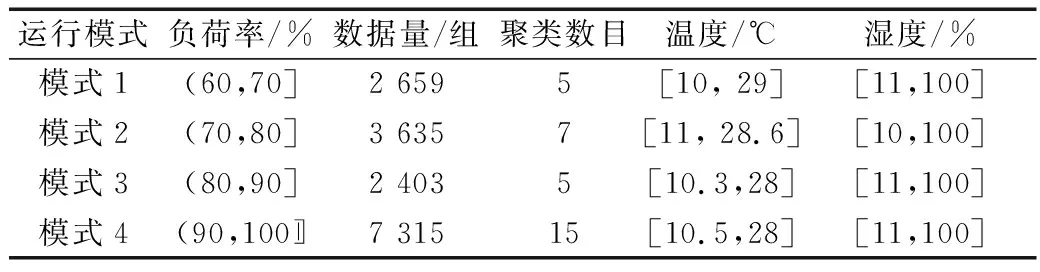
表3 運行模式劃分及聚類情況Table 3 Classification of the operating mode and clustering result

圖4 32種基本運行工況Fig.4 32 kinds of condition of basic operation
2.5 冷源機房設備多目標優化模型建立
為深入挖掘空調系統的最優運行參數,實現中央空調冷源機房設備的高效運行,采用多目標優化研究方法優化運行參數。基于運行機理建立冷水主機、冷凍泵、冷卻泵的能耗模型,進而確立目標函數。通常,中央空調系統運行參數的調節是通過在線控制系統完成的,控制系統能夠設置冷凍出水溫度、冷凍水流量、冷卻水流量、冷凍水溫差和冷卻水溫差等參數的目標值,控制系統通過調節電機頻率和設備運行臺數來間接調節冷凍回水溫度和冷卻回水溫度,因此,通過優化得到的最佳運行參數對提高空調運行能效具有指導意義。
故需要根據空調系統運行機理,建立冷源機房設備的多目標優化模型,包括系統總能耗模型和制冷量函數表達式。
2.5.1 冷水主機能耗模型
空調冷水機組的建模方式主要分為理論模型和經驗模型。現采用經驗模型,經驗模型是在研究冷水機組熱力學特性的理論基礎上,分析其與運行參數間的關系,從而建立一種數學模型的模糊表達形式。根據ASHRAE handbook推薦,將冷水機組的能耗擬合為冷凍回水溫度和冷卻回水溫度的函數,采用兩個二次多項式乘積的形式[14]。具體表達式為

(5)

2.5.2 冷凍水泵能耗模型
理論上,處于變頻條件下的水泵性能參數遵循相似定律,但在實際運行中,其運行工況點并不完全遵循相似定律。根據在變頻狀態下得到的水泵實際運行數據,研究得出水泵功率與流量是二次多項式關系[15]。考慮到各工況數據量的不同可能影響模型擬合的準確性,因而將功率與流量的關系確立為三次非線性表達式,具體表達式為

(6)
式(6)中:f2為冷凍水泵功率,kW;vcwh為冷凍水流量,m3/h;a0、a1、a2、a3為回歸系數。
2.5.3 冷卻水泵能耗模型
冷卻水泵流量可以通過調節電機功率實現變頻控制,冷卻水泵功耗模型與冷凍水泵功耗模型類似,擬合為流量的三次表達式為

(7)
式(7)中:f3為冷卻水泵功耗,kW;vcw為冷卻水流量,m3/h;b0、b1、b2、b3為回歸系數。
2.5.4 約束條件
建立有效的約束條件是實施有效優化的重要保障,在中央空調工程設計方案以及實際應用中,為保障系統性能以及空調運行的安全性,運行參數均有相應的數值控制范圍。對于指定的冷源機房,根據中央空調機組廠商規定的標準狀況下運行參數值并結合該中央空調控制系統中的實際運行參數設定范圍,能夠得到各設備運行參數范圍。決策變量均是連續型變量,以各變量閾值為準,建立多目標優化模型的約束條件,具體描述如下:
Tcl,min Tel,min vcwh,min vcw,min Tchws,min 2.5.4 多目標優化模型 對于確定的冷源機房設備系統,其總能耗與制冷量呈正相關關系,但較低的系統總能耗不一定得到較高的系統能效。系統能效比是制冷量與系統總能耗之比,為了優化后得到最佳能效,將系統能耗的最小值和制冷量的最大值設定為多目標優化的目標函數,冷源機房設備系統總能耗包含主機能耗和水泵能耗。目標函數的具體表達形式為 fmin(Tcl,Tel,vcwh,vcw)=f1+f2+f3 (8) Q=cvcwh(Tel-Tchws) (9) 式中:Q為制冷量,kW;c為水的比熱,J/(kg· ℃);vcwh為冷凍水流量,m3/h;Tchws為冷凍出水溫度,℃。 基于運行模式和工況劃分,統計一年中各種運行工況的有效數據量,選取4種運行模式下的數據量最大的工況作為典型運行工況來進行優化。采用最小二乘法將典型工況下的有效數據擬合多目標優化模型,再用NSGA-Ⅱ算法對模型進行優化。 多目標優化問題通常存在一個解集,這些解之間對于多個目標函數而言是無法比較優劣的,因為一個解改進一個目標函數的同時會削弱其他目標函數[16]。采用NSGA-Ⅱ算法優化系統模型,以最大制冷量和最小總能耗為優化目標函數。圖5展示的是4種運行模式下的典型工況Pareto前沿圖。根據多目標優化理論可知,Pareto前沿均可作為優化方案解。選取4種運行模式下能效最高的點作為最優解,如表4所示。 圖5 4種運行模式下的典型工況Pareto前沿Fig.5 Pareto frontier of Typical conditions in four operating modes 表4 4種運行模式下典型工況的Pareto最優解Table 4 Pareto optimal solutions under typical conditions in four operating modes 在以往的空調優化研究中,廣泛采用以空調系統能耗最低為目標函數的單目標優化方式來達到系統節能和能效提升的目的。文獻[17]建立以系統總能耗最小為目標并運用遺傳算法優化中央空調系統的運行參數,結果表明空調系統的節能率跟其部分負荷率有關,實際運行負荷越小,其節能空間越大。 將NSGA-Ⅱ算法的多目標優化方法與經典遺傳算法優化方法在相同工況下對冷源機房設備能效優化的效果進行比較。將建立的能耗模型作為唯一目標函數,采用經典遺傳算法對模型進行優化。運用單目標算法進行優化時,設置初始種群為100、交叉概率為0.7、最大進化代數為300。4種典型運行工況的單目標優化結果如表5所示。 表5 4種典型工況的經典遺傳算法單目標優化結果Table 5 Single-objective optimization results of the classic genetic algorithm under four typical conditions 圖6所示為兩種優化方式在不同工況下的平均循環性能系數(coefficient of performance,COP)對比情況,COP表達式如式(10)所示。從圖6可以看出,在提升系統運行能效方面,4種典型工況下的多目標優化方法相對于普通優化方法更具有優勢。 圖6 4種典型工況下的兩種優化方式COP比較Fig.6 Comparison of COP values of two optimization under four typical conditions (10) 最后,為驗證本文方法的實際參考價值,將4種運行模式下的典型工況進行優化前后對比分析,為更直觀地體現對比效果,在Pareto前沿上選取與優化前制冷量相同的優化解點,再進行比較驗證。如圖7所示為4種典型工況優化前后的能耗及能效的比較。 圖7 典型工況下多目標優化前后系統能耗、能效比較Fig.7 Comparison of energy consumption and energy efficiency on the air-conditioning system before and after multi-objective optimization under typical conditions 優化結果表明,4種典型工況經過多目標優化后,能效隨著制冷量的增大而持續增大,相對于實際運行工況,優化后有更穩定的運行參數。相較于系統原有運行方式,優化后的運行參數能明顯提高其運行能效,經過計算,多目標優化后系統能效平均提升14.35%,能耗平均降低12.52%。 將NSGA-Ⅱ算法用于冷源機房設備系統運行參數多目標尋優,得到4種典型工況下的Pareto前沿,從Pareto前沿分布看,各工況曲線光滑且解點在合理數值范圍,表明將NSGA-Ⅱ算法用于中央空調節能優化是可行的。 僅對單臺冷水主機實施參數優化,將多目標優化與普通優化方式相比較,發現多目標優化在提高系統運行能效上更具優勢,因為將制冷量作為目標函數能更好地得到冷凍進出水溫度的合理數值。 為提高本文方法的工程應用價值,將優化前后系統運行能耗和能效進行對比分析,各工況均有較好的優化效果,為空調實際運行時參數設置提供一定的參考價值。3 仿真實驗
3.1 Pareto優化結果


3.2 優化結果對比分析


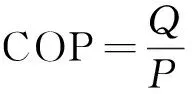
3.3 仿真驗證

4 結論

