引入四元數理論的改進粒子群算法

張曉聞, 任勇峰

(中北大學儀器與電子學院， 太原 030051)

粒子群算法(particle swarm optimization, PSO)[1]是一種模擬鳥群覓食行為的優(yōu)化算法，近年來，由于該算法簡單，參數設置少，容易跳出局部最優(yōu)，搜索到全局解被廣泛應用。傳統(tǒng)粒子群算法為不同的交互對象構造兩種不同的版本，全局最好模型(globalbest，Gbest)及局部最好模型(localbest，Lbest)。而近年來，學者們研究了很多不同的改進算法，文獻[2]中以Shi和Eberhart的粒子多樣性為基礎，給出了多種求解位置多樣性、速度多樣性及種群多樣性的方法，都取得了很好的效果。其他方面，文獻[3]中提出一種融合優(yōu)質粒子分布的粒子群優(yōu)化算法，在“社會”部分加入以分布估計算法為基礎的優(yōu)質粒子，該優(yōu)質粒子是根據統(tǒng)計學習概率模型而產生的。文獻[4]為了在擴大粒子搜索空間時避免陷入局部最優(yōu)，利用了正弦函數獨有的振動特性，在位置公式中加入正弦三角函數因子。有的學者根據反推理論，從反向學習的角度出發(fā)，文獻[5]利用反向學習策略進行改進，用反向解代替當前解，擇優(yōu)進行下一次迭代。文獻[6]在反向學習的基礎上，引入折射原理思想，對粒子群算法進行改進。還有研究學者利用小生境鄰域[7]的思想進行改進粒子群算法，其思想是粒子的鄰域結構隨著迭代次數的變化而變化。因此針對不同的問題提出適合該問題的鄰域結構，如文獻[8]提出了利用拓撲結構構造局部鄰域解。文獻[9]提出了一種帶有粒子聚合度的改進粒子群算法，該算法中融合了聚合度和慣性權重的概念，聚合度反映粒子聚集的程度，作用是使粒子跳出局部最優(yōu)。文獻[10]針對PSO算法的不確定動態(tài)多目標優(yōu)化問題，在位置更新公式中引入動態(tài)變異算子，通過分段線性函數參數化實現不確定動態(tài)多目標優(yōu)化。文獻[11]通過歷史數據學習模型避免算法陷入局部最優(yōu)。文獻[12-14]通過聚類模型和自適應模型改進算法，從而實現算法的收斂速度和搜索精度的平衡。

在以上改進算法中，都忽略了一個問題，無論學習機制、拓撲結構、引入算子模型及鄰域思想如何等，只是將各項學習之間看作相互獨立的個體，都忽略了學習機制之間的關系。為了使粒子的多樣性得到進一步利用，避免粒子群體過早收斂，現在樹狀拓撲結構的基礎上，將空間中的粒子利用拓撲結構分類，得到局部最優(yōu)解，利用四元數理論，將3種學習機制：自身最優(yōu)、全局最優(yōu)和局部最優(yōu)作為四元數的3個虛部向量，將四元數項作為相關項信息加入到粒子群算法中，用于調節(jié)3種記憶粒子之間的相互關系。粒子群算法的應用廣泛，可用于信號處理、圖像處理、濾波器等多個領域。

1 相關理論

1.1 樹狀拓撲結構

文獻[15]提出一種逐級尋優(yōu)拓撲結構(Tree-PSO，TPSO)，主要是一種基于樹狀的拓撲結構，如圖1所示，該結構中由子節(jié)點之間交流比較，得到上一層父節(jié)點，直到找到全局最優(yōu)值。

圖1 TPSO拓撲結構及節(jié)點分布Fig.1 TPSO topology and node distribution

1.2 四元數理論

四元數[16]是一個表示超復數的數學概念，它的構成是實部加上3個虛部單位i、j、k。每個四元數都可由1、i、j、k線性表出，則四元數的一般表達式為q=a+bi+cj+dk，其中a、b、c、d都為實數。當a=0時，q=bi+cj+dk稱為純四元數。近些年，四元數的應用廣泛，現利用四元數虛部的相關關系，對粒子群算法進行改進，無論在理論創(chuàng)新和實際應用中，都提供了新思路。

2 算法原理

2.1 基本思想

樹狀拓撲結構是結合粒子的3個最優(yōu)值來改變粒子的飛行方向，但無論是個體、局部還是全局的記憶適應值，都忽略了一個問題，就是三者之間的相關性，為了將三者之間的聯系用來調節(jié)粒子的飛行方向，提出了一種結合四元數理論的改進粒子群算法，利用TPSO作為模型，將個體最優(yōu)、局部最優(yōu)和全局最優(yōu)作為四元數的3個虛部，將四元數作為關聯項加入粒子群速度公式的“社會”部分。同時在公式中使用了慣性權重和收縮因子，以保證群體可收斂到全局最優(yōu)值。

當a=0,b=c=d=1時，將單位純四元數q=i+j+k代入PSO公式，則改進算法的速度與位置公式為

vi+1,j=χ[wvi,j+c1r1(pi,j-xi,j)+c2r2(pn,j-xi,j)+

c3r3(pg,j-xi,j)+c4r4(qi,j-xi,j)]

(1)

xij(t+1)=xij(t)+vij(t+1)

(2)

式中：x為位置；v為速度；i為當前粒子；j為當前維數；t為當前迭代數；qi,j=pi,j+pn,j+pg,j，pi,j記錄粒子個體的最佳解，pn,j記錄局部鄰域內的粒子最佳解，pg,j記錄全局粒子的最佳解；χ為收縮因子；w為慣性權重；c1為調節(jié)個體最優(yōu)的加速系數；c2為調節(jié)局部最優(yōu)的加速系數；c3為調節(jié)全局最優(yōu)的加速系數；c4為調節(jié)三者關系的加速系數；r1、r2、r3、r4∈(0,1)且相互獨立。

2.2 算法步驟

根據改進算法的設計，下面給出算法的步驟。

步驟1對算法的基本參數進行初始化。

步驟2根據優(yōu)化函數，計算適應值，并比較記錄pi,j、pn,j和pg,j。

步驟3根據步驟2中記錄的pi,j、pn,j和pg,j，計算四元數項。

步驟4將四項記錄值代入式(1)、式(2)，得到最新迭代次數下的粒子速度和位置。

步驟5根據循環(huán)終止條件判斷是否滿足終止，否則返回步驟2。

在每次迭代中，粒子向全局最優(yōu)、局部最優(yōu)及個體最優(yōu)學習的同時，還保留著三者之間的相關性，此方法使粒子的多樣性得到充分利用，避免種群陷入了局部最優(yōu)而導致無法找到最優(yōu)解。

2.3 算法收斂性證明

基本微粒群算法中給出了判斷PSO收斂性的兩個假設條件及全局收斂準則[17-19]。在保證算法有效的前提下，設D為算法迭代方式，用來得到下一次的迭代值，則由D得到的當前迭代值應優(yōu)于前一次迭代值。因此，提出下列假設以滿足算法。

假設1f[D(z,ξ)]≤f(z)，并且如果ξ∈S，S∈Rn，則f[D(z,ξ)]≤f(ξ)。

假設2對于樣本空間S的任意Borel子集A，若其測度v(A)>0，則有

(3)

式(3)中：μk(A)為由測度μ(k)所得到的A的概率。

由假設1和假設2給出算法為全局收斂的充要條件。

(4)

式(4)中：P[zk∈Rε]為第k步算法生成的解zk∈Rε的概率。

根據以上假設及定理，證明改進的PSO算法的收斂性。

證明：定義函數D為

(5)

式(5)中：g(xi,k)為改進PSO算法的更新方程。具體為

xi,k+1=g(xi,k)=g1(xi,k)+g2(xi,k)+g3(xi,k)+g4(xi,k)+g5(xi,k)

(6)

式(6)中：g1(xi,k)=xi,k+ωvi,k，g2(xi,k)=c1r1(pi,k-xi,k)，g3(xi,k)=c2r2(pn,k-xi,k)，g4(xi,k)=c3r3(pg,k-xi,k)，g5(xi,k)=c4r4(qi,k-xi,k)，xi,k為第k代時的微粒i的位置，則由定義函數D可知，改進PSO滿足假設1。

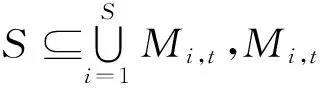
Mi,k=(1+ω-φ1-φ2-φ3-φ4)x(t)-ωx(t-1)+piφ1+pnφ2+pgφ3+qφ4=xi,j,k-1+ω(xi,j,k-1-xi,j,k-2)+φ1(pi-xi,j,k-1)+φ2(pn-xi,j,k-1)+φ3(pg-xi,j,k-1)+

φ4(q-xi,j,k-1)

(7)

3 仿真實驗

3.1 測試函數

選擇的6個基準測試函數(其中兩個單峰值函數，兩個多峰值函數及兩個多峰固定維度測試函數)如表1所示，對算法進行驗證，尋找函數的最小值，并將基本PSO、EDAPSO、TPSO和本文算法對基準函數優(yōu)化的結果進行比較分析。通過實驗的數據來觀察在同一測試函數下算法的收斂效率和搜索精度。

3.2 參數設置

根據實驗所需參數，對參數的設置如下：最大迭代次數為1 000,慣性權重ω=0.8，收縮因子χ=0.729。粒子規(guī)模=30。經實驗得到，在本文算法中，c1、c2、c3代表粒子分別向個體最優(yōu)、局部最優(yōu)和全局最優(yōu)學習的隨機數，c4代表向三種粒子相關項學習的隨機數。當c1=1.4,c2=1.4,c3=1.8,c4=1.4時，取得的效果較好。

3.3 實驗結果

3.3.1 仿真實驗分析

為了便于考查不同算法的性能，將PSO、EDAPSO、TPSO和本文算法進行比較，將每個算法分別對表1的6個測試函數獨立運行30次，記錄每種算法在各個函數下的最大值、最小值、平均值及平均時間，具體實驗結果如表2所示。對比表2中數據，表明本文算法相對于PSO、EDAPSO和TPSO具有明顯的優(yōu)勢。由于在本文算法中加入了四元數為關聯的三個記錄值，比較表中的數據可以發(fā)現，對比最小值結果和函數的最優(yōu)值，本文算法尤其在F1、F3、F5和F6中可收斂于全局最優(yōu)值。對于單峰值函數，比較幾種算法的平均值可以得出，平均值至少提高10倍，對于F2函數，收斂的平均值有了質的提升，即本文算法在搜索的精度上比其他三種算法高，粒子的多樣性得到充分利用。

表1 基準測試函數Table 1 Benchmark function

表2 函數測試結果Table 2 Function test results

對于多峰值函數，在整個函數搜索空間中會包含大量的局部極值，對于PSO算法來說，容易使其陷入局部極值，而本文算法由于利用了TPSO的樹狀結構，同時加入了四元數項，以使粒子的多樣性得到充分利用，使得算法在學習過程中達到了平衡，更容易跳出局部最優(yōu)值，從而能繼續(xù)搜索全局最優(yōu)值。對于多峰固定維測試函數，因其解空間維度較低，不同算法得到的解差異不大，雖然都沒有找到真值，但本文算法搜索結果更優(yōu)。通過幾種算法應用于同一約束函數的收斂曲線如圖2所示，明顯看出本文算法的收斂性優(yōu)于其他3種算法。

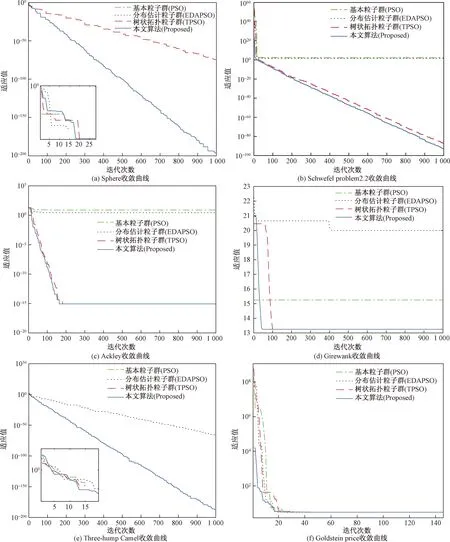
圖2 算法的收斂曲線對比Fig.2 Convergence curves comparison of algorithms

3.3.2 物理實驗分析

文獻[20]中利用粒子群優(yōu)化算法結合伽馬校正，來評估所獲得的紅外圖像增強結果。借鑒此經驗，選取圖像集中的3幅圖像進行對比度增強實驗，增強后效果如圖3所示：將本文算法與PSO算法進行對比度圖像增強算法比較，采用5個圖像質量準則進行性能評價，評價結果如表3～表5所示。評價準則包括：峰值信噪比(peak signal to noise ratio, PSNR)；結構相似度指數測度(structural similarity, SSIM)；信息保真度準則(information fidelity criterion, IFC)；視覺信息保真度(visual information fidelity, VIF)；特征相似性(feature similarity, FSIM)。所有這些準則都被廣泛應用于圖像對比度增強領域，對各種圖像對比度增強方法進行性能評價。物理實驗中PSO算法的參數設置如下:種群大小為30，最大迭代次數為1 000，c1、c2、c3代表粒子分別向個體最優(yōu)、局部最優(yōu)和全局最優(yōu)學習的隨機數，取c1=1.4,c2=1.4,c3=1.8。

圖3 測試圖像對比Fig.3 Test image comparison

表3 測試圖像1對兩種方法性能評估Table 3 The performance evaluation of two approaches using test images 1

表4 測試圖像2對兩種方法性能評估Table 4 The performance evaluation of two approaches using test images 2

4 結論

改進的粒子群算法在TPSO樹狀結構的基礎上，選擇局部最優(yōu)的粒子節(jié)點，與個體最優(yōu)粒子和全局最優(yōu)粒子之間相關聯，通過四元數的數學概念，將這三者設為四元數的三個虛部向量，作為社會部分，加入速度公式中。對改進的算法通過理論證明算法具有全局收斂性，通過仿真實驗對算法的收斂性進行可視化說明，改進的PSO算法不但減緩粒子群優(yōu)化算法的收斂，而且有效地解決了搜索精度不高和容易陷入局部最優(yōu)值的問題。在算法效率上通過與PSO、EDAPSO和TPSO進行分析比較，具有顯著的算法性能，既驗證了它的理論可行性，又仿真了算法的實驗可行性。對所提算法與其他進化算法優(yōu)化對比度增強進行比較，選擇兩個不同數據集中的圖像進行主觀與客觀評價，最后結果得出，無論在主觀定性方面還是客觀定量方面，本文算法的效果都要優(yōu)于其他算法。