基于MATLAB 的核密度估計研究

王萌萌 梁瀘丹 寇俊克

（桂林電子科技大學數學與計算科學學院，廣西 桂林 541004）

0 引言

在數理統計研究中，密度估計一直是一個極其重要的熱門研究問題。 其研究成果被廣泛應用到經濟學、社會學以及生物統計等領域[1-4]。 特別是當前大數據時代，如何對數據進行高效地分析處理以便找出數據之間的特征規律就顯得尤其重要。密度估計作為數據分析的一種有效工具，能夠高效地找到數據所蘊含的分布規律，這為后續數據分析處理提供了重要的參考依據。密度估計研究的本質問題是如何高效地利用觀測數據找到數據的分布規律。常規密度估計方法分為參數估計和非參數估計兩類。參數估計方法需要事先假設數據滿足某個特定的模型或者有先驗知識可以參考。 然而在實際應用中，對于獲取的數據事先沒有任何先驗知識可以利用且無法確定數據滿足哪些模型，因此，參數估計方法有一定的局限性，無法廣泛應用。 相反，非參數估計方法不需要借助任何先驗知識，僅僅利用數據本身信息進行估計，因而在實際應用中得到了廣泛的應用。

在非參數估計方法中，核密度估計方法以其原理簡單易懂且操作便捷而備受關注。核密度估計方法不需要先驗知識，且能夠處理較為復雜的數據，同時其估計效果也十分理想。 鑒于上述特點，核密度估計方法被廣泛應用于公共事務、地理信息、醫療教育等多個領域[5-8]。核密度估計方法估計效果的優劣其關鍵在于核函數的選取以及帶寬的選擇。 針對這一問題，本文將借助MATLAB 軟件進行數值模擬實驗， 對比分析不同核函數、不同帶寬以及不同樣本容量對密度估計效果的影響。通過實驗分析核密度估計方法參數選取的優劣性，以期為當前大數據處理提供理論依據。

1 核密度估計理論

核密度估計方法作為非參數密度估計的經典方法之一，在大數據處理中發揮著極其重要的作用。本文首先簡要介紹核密度估計方法的原理。 在某一事件概率分布未知的情況下，利用觀測數據進行密度函數估計。另外， 數據之間由于距離的遠近也會產生不同程度的影響。 故認為距離較近的數據互相之間產生的影響較大，而距離較遠的數據產生的影響較小。核密度估計方法正是基于上述思想建立起來的。

設隨機變量X1，X2，…，Xn是從總體中抽取的獨立同分布樣本，其密度函數為f（x），則核密度估計器（為其中，n 為樣本容量，h 為帶寬，K（x）表示核函數。作為核密度估計方法的核心，其核函數應具備以下條件：（1）非負性K（x）≥0；（2）對稱性K（x）=K（-x）；（3）歸一性∫RK（x）dx=1。 針對核密度估計器（f（x）來說，通過觀察發現該方法主要強調當隨機變量Xi與變量x 的絕對值越小， 則兩者距離越小， 進而隨機變量Xi對點x 處的密度函數值影響越大。另外，核密度估計器只依賴于樣本數據、帶寬以及核函數，對于樣本數據是否滿足特定的模型或者規律不做要求。

針對核密度估計器來說，只要其核函數以及帶寬選取得當，核密度估計方法可以以任意精度去逼近真實密度函數。 常規核函數主要有表1 所示的幾種。

表1

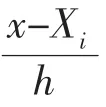
2 數值實驗

針對核密度估計問題，不同核函數、不同帶寬以及不同樣本容量都會對估計效果產生影響。鑒于上述參數的重要性， 本文下面將借助MATLAB 軟件進行核密度估計數值實驗對比分析[9-10]。

2.1 不同核函數實驗

本節將分別選取高斯核、均勻核、三角核以及二次核函數進行實驗對比分析。 首先，利用MATLAB 軟件隨機生成1 000 個服從標準正態分布的隨機樣本數據；然后，針對這1 000 個樣本數據分別選用高斯核、均勻核、三角核以及二次核進行密度估計實驗，其實驗結果如圖1 所示。

從圖1 可以看出，4 種核函數估計結果均呈現正態分布形態。這說明當樣本數據大致呈正態分布的時候，上述4 種核函數都能取得不錯的估計效果。但是，不同核函數的估計效果仍存在比較明顯的差異，其差異性主要表現在X 軸的負半軸以及峰值附近。高斯核函數和二次核函數在X 軸負半軸的估計效果要優于三角核與均勻核。 另外，在峰值處雖然估計值均比真實值小，但是高斯核峰值附近產生差異的區間要小于其他核函數。 從整體上來說，4 個核函數的估計結果與真實密度函數大體保持一致，所得到的密度估計曲線基本相同。

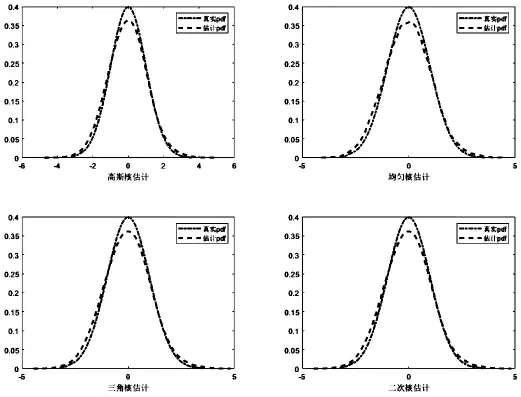
圖1 不同核函數估計結果

2.2 不同帶寬實驗

在核密度估計方法中，帶寬的選取會對估計效果產生很大的影響。 前文已經通過分析核估計器的函數特性說明了這一點。 下面將通過數值實驗對比分析帶寬選擇的優劣性。 首先，利用MATLAB 軟件生成100個服從正態分布的隨機樣本數據，核函數選擇高斯核函數。 為了更加充分地分析帶寬選擇對估計效果產生的影響，帶寬依次選擇h=1，h=3，h=5 以及h=10。 其實驗結果如圖2 所示。

從圖2 可以看出，對于同一組樣本數據且核函數相同的情況下，當帶寬為1 時，曲線波峰過多且參差不齊，過分細化導致密度估計波動太大，從而喪失了密度估計的意義。當帶寬h=10 時，數據平均化過于突出，密度估計太過平穩，從而使得估計值與真實值偏差過大。 由此可知，帶寬選取過小或過大都會使密度估計值與真實值偏差過大。 另外，從圖2 也可以看出當帶寬h=3 時估計結果與真實密度函數圖像幾乎完全重合， 這就意味著在此帶寬條件下估計效果最好。綜上可知，帶寬的選取對核密度估計效果具有顯著的影響。

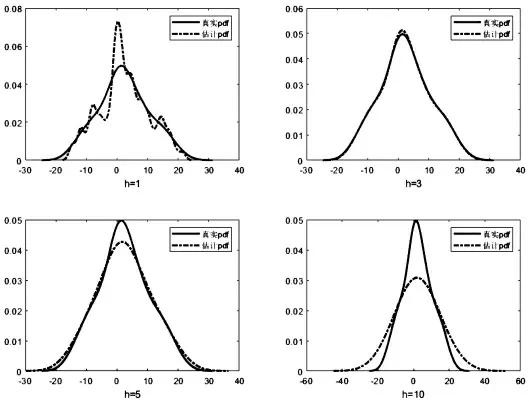
圖2 不同帶寬估計結果

2.3 不同樣本容量實驗

針對核密度估計問題，樣本容量的大小也會對估計效果產生影響。 一般來說，可以利用的有效數據越多，則估計效果就越好。 為了充分分析樣本容量對估計效果好壞的影響，在同一帶寬和核函數的條件下對比分析不同樣本容量的估計結果。分別進行樣本容量為20、50、100、1 000 的數值實驗， 其實驗結果如圖3所示。

由圖3 可知，當樣本容量過小時（n=20），其估計結果與真實密度函數相差太大，尤其在峰值處更為突出。 當樣本容量過大時（n=1 000），雖然其估計結果與真實密度函數大體一致，但是在峰值處仍存在較大差異。 當樣本容量為100 時，其核估計結果與真實密度函數圖像幾乎重合，估計效果最好。 另一方面，對比樣本容量20，50，100 的估計結果可以得出， 隨著樣本容量的增大，核密度估計效果越來越好。 但是這并不意味著樣本容量越大越好， 這一觀點可以從樣本容量1 000 時的估計結果可以看出。

綜上分析可知，在帶寬固定的條件下，樣本容量選取過小，數據細化作用突出，估計偏差較大，無法反映出真實數據的特性；樣本容量選取過大，估計效果整體偏好，但是在峰值附近誤差過大。

3 結論

針對密度估計問題， 本文借助MATLAB 軟件分析了核密度估計方法關鍵參數核函數、帶寬以及樣本容量對估計結果的影響。 通過實驗對比分析發現，核函數的選取對于估計效果的好壞影響不大，但是帶寬以及樣本容量的選取對于估計結果的影響程度較大。其次，帶寬過小或者過大都會導致密度估計結果與真實密度函數偏差較大，因此，必須選擇合適的帶寬才能得到理想的估計效果。 另外，樣本容量并不是越大越好，而是應該在一個合理的范圍之內。最后，對于密度估計問題，核密度估計方法必須依據數據的某些特征，合理恰當地選取核函數以及帶寬，并利用一定數量的樣本數據進行密度估計，以期得到更加理想的估計結果。