雜波條件下利用一維卷積神經網絡的認知雷達波形設計

趙俊龍，李偉，甘奕夫，鄒鯤

(西安空軍工程大學信息與導航學院，710077，西安)

2006年,加拿大學者Haykin根據海豚、蝙蝠等生物的回波定位系統首次提出認知雷達的概念[1]。與傳統雷達相比,認知雷達具有智能信號處理、發射機與接收機之間形成閉環反饋、保存雷達回波信息等特點[2-3]。作為未來雷達的主要發展趨勢,認知雷達通過與環境的交互,改變雷達發射波形,使雷達更適應環境。因此,波形設計是認知雷達中最重要組成部分之一[4-5]。

波形設計的本質是準則函數加約束條件的最優求解問題[6]。其中,準則函數的選擇取決于雷達任務。針對目標參數估計或目標識別任務,Bell提出用最大化目標與雷達回波之間的互信息量(MI)來設計波形[7],更多的互信息量意味著可以通過回波獲取更多關于目標的信息,減小目標的不確定性,更清晰的刻畫目標特征,該方法被稱為MI方法。Guo等證明了在目標參數估計問題上,MI方法與最小均方差(MMSE)方法是等價的[8]。對于高斯噪聲下特定目標的檢測問題,Guerci與Pillai提出信干噪比(SINR)準則來最大化雷達接收信號的信干噪比設計最優檢測波形,并取得了良好的結果[9],該方法稱為SINR方法。上述文獻僅考慮了噪聲對波形設計的影響,而忽略了雜波的影響。為解決雜波條件下目標識別和目標檢測問題,Romero等針對確定目標和擴展目標在噪聲和雜波背景下,通過MI方法和SINR方法分別設計波形,并推導出MI方法與SINR方法之間的關系,為波形設計領域提供了比較完整的理論[10]。隨著雷達技術的發展,雷達任務和工作模式日趨多樣化,不僅需要進行目標檢測,同時還需要對目標參數進行估計和目標識別,基于單個準則設計的雷達波形已經難以滿足需求,這就需要更加靈活的波形設計框架來聯合不同的設計準則進行雷達波形設計[11]。然而,由于不同準則之間的數學關系難以建立,或者建立的數學關系缺乏針對性,因此學術界對這一領域的研究還較少。

深度學習對函數的擬合能力為聯合不同準則問題提供一種解決思路。當下,隨著硬件計算能力的提升,深度學習成為研究熱點,其可有效提取數據特征,學習數據之間的內在規律,并在圖像處理、機器翻譯、自動駕駛等領域[12-13]取得了前所未有的成就。近年來,基于不同應用場景,學者們提出了一系列深度學習模型,其中,卷積神經網絡(CNN)是應用最為廣泛的模型之一,常用于二維數據處理。隨著技術需要,適用于處理一維數據的一維卷積神經網絡(1D-CNN)逐漸應用在語音識別[14]、自然語言處理領域[15],也廣泛應用在雷達領域[16]。為解決聯合不同準則問題,本文提出一種雜波條件下利用1D-CNN的認知雷達波形設計方法(CRWD-1D-CNN)。

本文首先分析了MI方法和SINR方法設計波形的過程,得到了目標函數的表達式,并設定環境信息,使用兩準則設計信號,構建訓練集;其次,介紹了1D-CNN網絡結構,提出使用1D-CNN來聯合MI方法和SINR方法的流程圖。在此基礎上,根據訓練集數據形式設計了1D-CNN模型;最后,對1D-CNN模型進行訓練和測試,并通過實驗仿真,對比1D-CNN生成信號、MI方法信號和SINR方法信號對應的檢測概率、目標識別率以及雷達綜合性能指標,證明了本方法可聯合MI方法和SINR方法,提高雷達綜合性能。

1 信號模型與波形設計方法

1.1 信號模型

圖1為擴展目標信號模型圖,其中x(t)是時寬為T、帶寬為W的雷達發射信號,擴展目標脈沖響應h(t)為有限時間Th內的零均值隨機過程,c(t)為隨機雜波脈沖響應,n(t)為雷達接收機端加性高斯白噪聲,y(t)是雷達接收機接收信號,r(t)為持續時間為Tr的理想低通濾波器。x(t)的傅里葉變換為X(f),h(t)的傅里葉變換為H(f),c(t)的功率譜密度(PSD)為Sc(f),噪聲h(t)的功率譜密度為Sn(f)。設T遠大于Th和Tr,即低通濾波器持續時間相對較短,可忽略其影響。

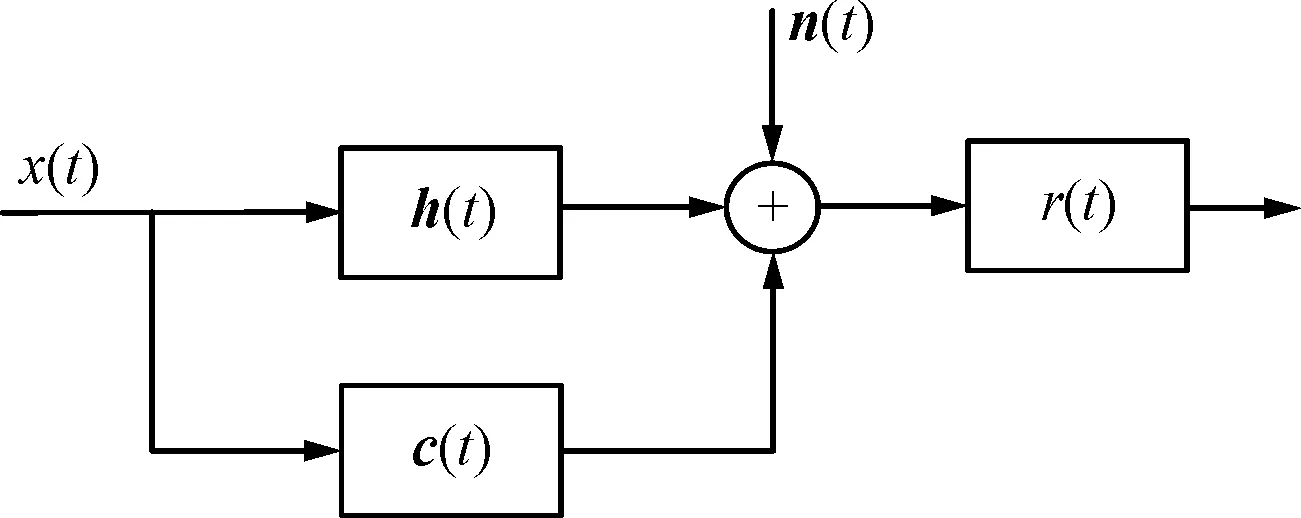
圖1 擴展目標信號模型

由于h(t)是在時間T內的局部平穩過程,所以不能用PSD來描述。但可以使用能量譜密度(ESD)來描述,定義ESD為

ξ(f)=E[|H(f)|2]

(1)

式中:E(·)表示取期望;H(f)的均值和方差分別為

μ(f)=E[H(f)]

(2)

σ2(f)=E[|H(f)-μ(f)|2]

(3)

其中σ2(f)為目標能量譜方差(ESV),由于擴展目標是0均值隨機過程,故σ2(f)=E[|H(f)|2],即ESV與ESD等價,可用ESV描述0均值有限時間隨機過程。由圖1可知,雷達接收信號為

y(t)=x(t)*h(t)+x(t)*c(t)+n(t)

(4)

1.2 MI方法

目標與雷達接收信號之間的互信息量為[10]

IM=I(y(t)；h(t)|x(t))=

(5)

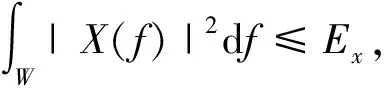
(6)

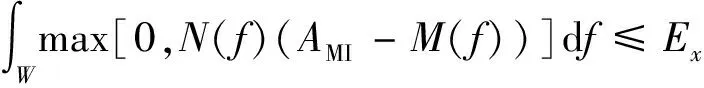
上述過程即為MI方法設計波形的過程。

1.3 SINR方法

雷達接收機接收信號的信干噪比[10]為

(7)

積分內函數為凹函數,結合能量限制,使用拉格朗日乘子技術求解得到優化波形為

(8)

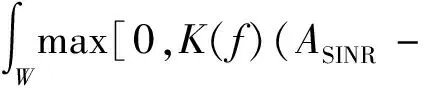
當信號經由存在干擾或噪聲的環境時,最佳傳輸信號在頻域的能量分布應避開干擾或噪聲能量較強的頻點,具有特定的能量譜分布。由MI方法和SINR方法設計波形的過程可知,兩方法設計波形時將擴展目標、雜波和噪聲建模為隨機過程,并使用能量譜方差σ2(f)描述目標特性,用功率譜密度Sc(f)和Sn(f)來描述雜波和噪聲特性。由式(6)和式(8)可知,忽略信號的相位信息,僅從頻域出發,即得到最優信號的頻域能量分布的幅度譜平方,達到信號設計的目的。

2 基于1D-CNN的雷達波形設計

2.1 1D-CNN模型

自2012年AlexNet在ImageNet大規模視覺識別競賽(ILSVRC)中取得前所未有的精度并奪冠[17]以來,CNN已經在計算機視覺領域取得了極大成就。典型的CNN可有效提取二維數據的結構特征,通常用于處理圖片等二維數據,為適應語音、文本等一維數據的處理,許多學者也提出了1D-CNN模型[18]。1D-CNN結構如圖2所示,通常由輸入層、卷積層、池化層、全連接層、輸出層等網絡層組成。

卷積層具有稀疏連接和權值共享的特征。稀疏連接可避免全連接神經網絡參數過多問題,而權值共享則可減小網絡的過擬合。1D-CNN卷積層中為一維卷積核,卷積層的作用是使用一維卷積核在前一層輸出特征圖上平滑移動進行卷積操作,提取數據特征。如圖2所示,第l卷積層的第j個輸出的卷積特征圖為

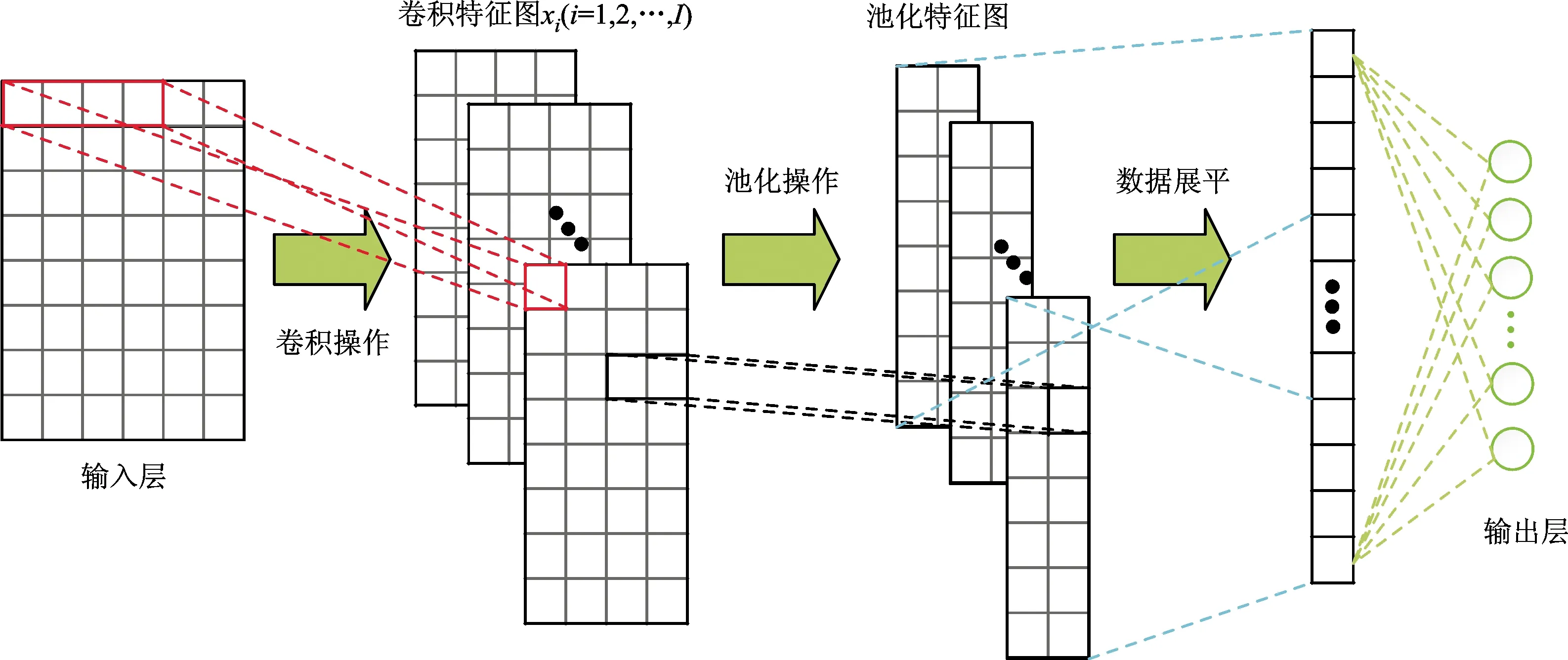
圖2 1D-CNN結構圖

(9)

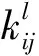
卷積層之后為池化層,其作用為對卷積特征圖進行下采樣操作,減小特征維度,提高特征魯棒性。通常有最大池化和平均池化兩種函數,最大池化僅保留局部特征中最大的數據點,而平均池化將局部特征數據取平均操作,具體池化操作的選區由任務性質而定。

經卷積層和池化層處理之后的數據可稱之為原始數據的深層特征,全連接層的目的就是將這些深層特征進行展平操作,來完成回歸或識別任務。

2.2 基于1D-CNN的雷達波形設計流程

由于聯合不同準則進行波形設計面臨目標函數難以建立的問題,神經網絡的學習能力為該問題提供一種解決思路。神經網絡的本質就是擬合函數,給定輸入和輸出數據,經過訓練,神經網絡即可擬合輸入數據與輸出數據之間的非線性關系,也即函數關系。此時神經網絡內部參數具備刻畫輸入數據與輸出數據之間非線性關系的能力,而這些參數的確定是由給定數據決定的。當輸入數據給定為目標、雜波、噪聲等環境信息,而輸出數據一部分是由MI方法根據環境信息設計的信號,另一部分是SINR方法設計的信號,經過訓練,神經網絡便可同時完成對MI方法函數和SINR方法函數的擬合,從而達到聯合MI方法和SINR方法的目的。

基于上述思想,本文提出一種雜波條件下使用1D-CNN的認知雷達波形設計方法,其設計信號的思想如圖3所示。由圖3可知,本文方法主要分為3個部分:首先,分析1D-CNN進行波形設計時的影響因素,因為利用MI方法和SINR方法進行波形設計時的影響變量為目標、雜波、噪聲,故1D-CNN的影響因素同樣為目標、雜波、噪聲等環境信息,在此基礎上設定環境信息,并分別使用MI方法和SINR方法根據這些信息來設計信號;其次,隨機選取一部分MI方法信號和一部分SINR方法信號,并和與之相應的環境信息共同組成訓練集,然后根據訓練集數據形式設計相應的1D-CNN模型;最后,使用訓練集對設計的1D-CNN模型進行訓練,并測試其性能。

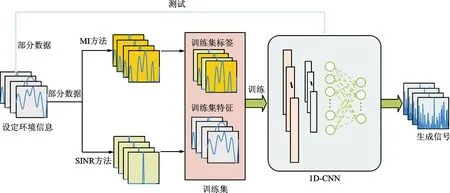
圖3 CRWD-1D-CNN方法流程

2.3 1D-CNN的設計

本文設計了一個由輸入層、卷積層1、池化層1、卷積層2、池化層2、卷積層3、池化層3、Dropout層、Flatten層、全連接層1、全連接層2及輸出層組成的1D-CNN模型,各層詳細參數如圖4所示。本文所用數據是在σ2(f)、Sc(f)、Sn(f)上采樣100點得到的,且訓練樣本為6 000組,設定輸入層信道為1,故輸入數據尺寸為(6 000,300,1)。圖4中,32@(11×1)表示32個維度為(11,1)的一維卷積核。

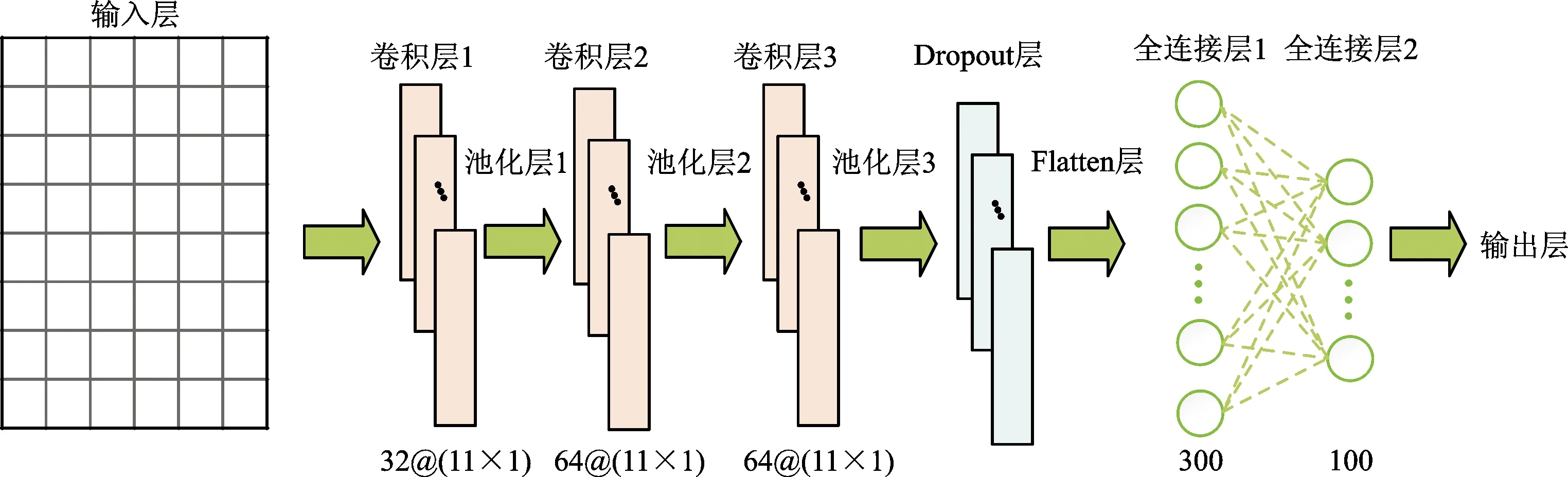
圖4 本文設計的1D-CNN模型圖

為減小網絡的過擬合,在將數據展平前加入Dropout層,其作用是在訓練過程中將部分神經元隨機失活,使得神經網絡以較少的神經元完成訓練,從而避免過擬合問題。Dropout層丟失率設為0.5。

在卷積層提取的特征進入全連接層之前,需要Flatten層對提取到的特征進行展平操作,使之轉換為更適應于全連接層處理的數據形式。由于1D-CNN在本文執行回歸任務,故在輸出層前添加兩層全連接層。最后輸出對應MI準則和SINR方法生成波形的頻域能量分布對應的采樣點數據,故第2個全連接層神經元數量設為100,第一個全連接層神經元數量設為300。

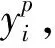
(10)

本文使用Adam優化算法,其中學習率ε=0.01,迭代2 000次,每次迭代批次數設為100。

3 實驗仿真

本實驗是在TensorFlow,MATLAB2017,Python3.6和CUDA9.0的環境架構中進行的,計算機的處理器為i5-7300 HQ,顯卡為GTX1050,內存為8 GB。

假設某雷達中心頻率fc=10 GHz,帶寬W=100 MHz,工作頻帶為[9.95,10.05]GHz。發射信號時寬為10 ms,其頻帶內采樣點為100。本文采取計算機模擬仿真的方法進行實驗數據的選取,為保證數據的充分性,設定4 000組雜波,雜波PSD通常為高斯分布[19],對于i∈[1,4 000],設Scc(f)=Bexp(-0.8α(f-fi)2),其中fi=fc+W/2-2.5×104i為雜波中頻,B=7.957 7×10-16為目標脈沖響應的譜方差強度,α表示譜方差隨頻率變化率,取α=1×10-13。為保證目標數據的非相關性,對于每組雜波,隨機產生一組目標能量譜方差,借鑒文獻[7,10],本文將目標能量譜方差幅度與雜波功率譜密度幅度取為相同值,共生成4 000組目標能量譜方差。假設雷達接收機端噪聲為高斯白噪聲,為盡可能體現雷達工作環境中噪聲遠遠低于目標的關系,噪聲功率譜密度取為Sn(f)=kT=4.143 0×10-21J,其中T=300 K為噪聲有效溫度,k=1.381×10-23J/K為玻爾茲曼常數。將上述每個雜波對應的目標和噪聲構成一組環境信息,共生成4 000組環境信息。

獲得環境信息之后,分別使用MI方法和SINR方法根據上述4 000組環境信息設計波形,對于每種準則信號隨機抽取3 000組環境信息與其對應環境信息組成包含6 000組樣本的訓練集,剩下1 000組環境信息作為測試集。然后,使用訓練集對設計的1D-CNN模型進行訓練。最后,使用測試集中的環境信息對訓練完成的模型進行測試。

每組環境信息包含3個變量,即雜波功率譜密度、目標能量譜方差、噪聲能量譜方差。測試集中包含1 000組環境信息,隨機抽取一組如圖5所示的環境信息,其中圖5a為雜波的能量譜密度Sc(f),圖5b是噪聲的功率譜密度Sn(f),由上述內容可知,Sn(f)為固定值,圖5c是目標的能量譜方差σ2(f)。

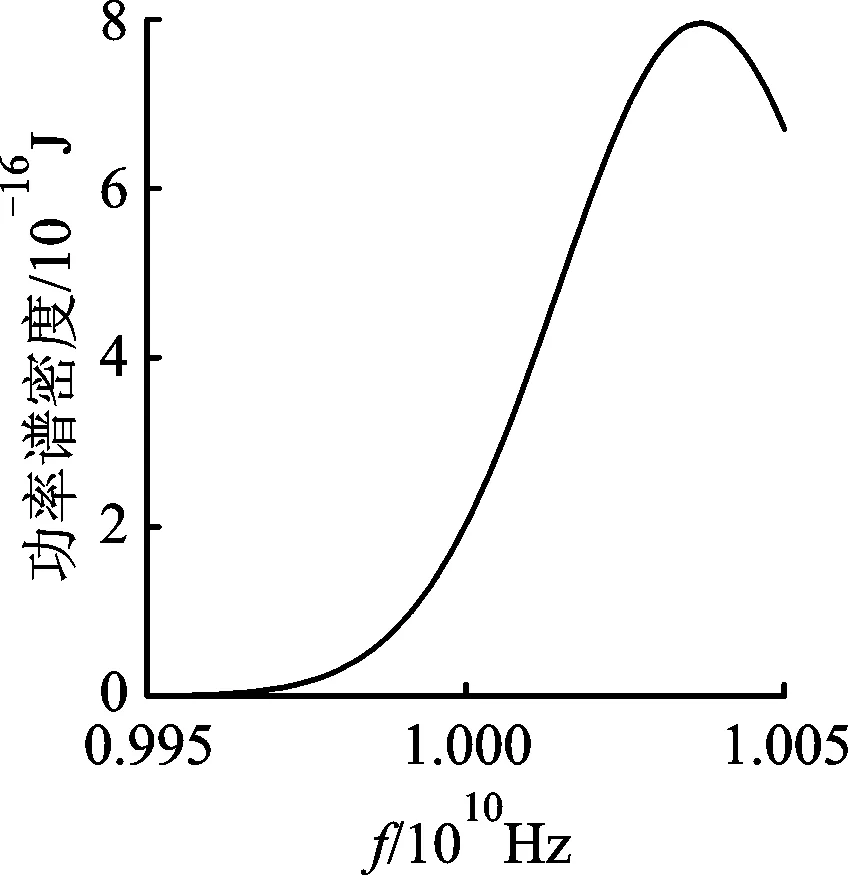
在雷達發射功率P=100 W時,使用圖5中的環境信息對訓練完成的1D-CNN模型進行測試,并與MI方法和SINR方法信號進行對比,結果如圖6所示。由圖6可知,3種信號在分配能量時都避開了雜波較強的頻點。MI方法信號頻帶較寬,各頻點分配的能量相對較低。SINR方法信號頻帶相對較窄,此窄帶內頻點能量較高。這是由于MI方法信號為獲取目標更多信息,需將能量分配到目標不同散射模式的頻點處,而SINR方法信號只需將能量分配到目標最大反射模式的頻點處。但是反射較弱的頻點可能包含較為明顯的目標特征,可用于目標識別。所以,MI方法信號通常用于目標識別,SINR方法信號用于目標檢測。CRWD-1D-CNN方法生成的信號頻帶介于兩信號之間,可兼顧目標不同的散射模式,既可獲得關于目標的較多信息,又可維持較高的信干噪比,實現了MI方法與SINR方法的平滑過渡。

(a)雜波功率譜密度

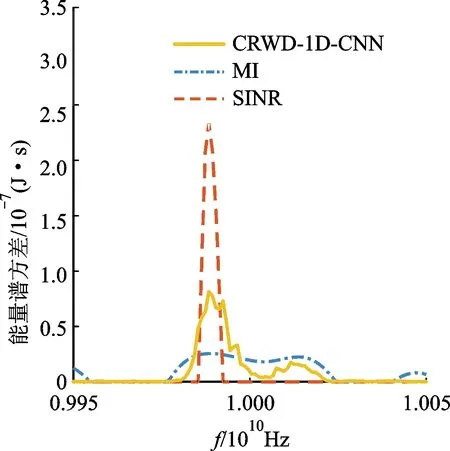
圖6 3種方法生成信號的頻域能量分布圖

本文使用蒙特卡羅方法對不同能量下1D-CNN模型進行測試。給定發射機能量,使用測試集中環境信息對訓練完成的1D-CNN模型進行測試,生成1 000組波形。對1 000組波形的互信息指標和SINR指標取平均,得到該能量下的互信息和信干噪比指標,其結果如圖7～圖9所示。

圖7為雷達不同發射功率下MI方法、SINR方法和CRWD-1D-CNN方法生成信號對應的互信息量指標。由圖可見,3種方法生成信號對應的互信息量都隨雷達發射功率的增加而增加,且CRWD-1D-CNN生成信號對應的互信息量要比SINR方法信號平均高出20.10%,比MI方法信號平均低8.24%。

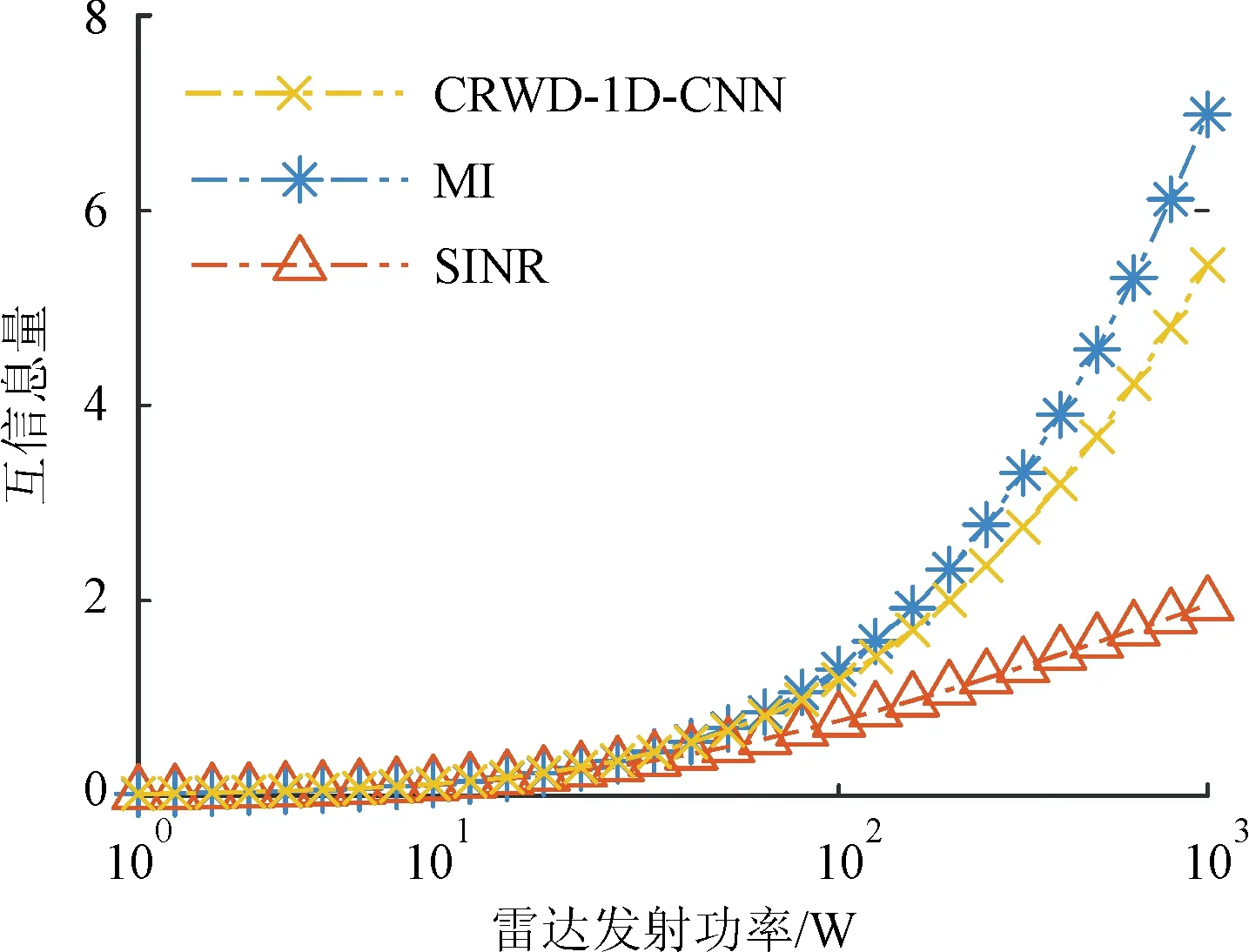
圖7 不同功率下3種方法生成信號對應的互信息

根據統計判決理論,雷達檢測可視為假設檢驗問題,解決該問題的基本方法為經典奈曼-皮爾遜(NP)定理,根據NP定理構造雷達檢測器,得雷達檢測概率為[20]

(11)

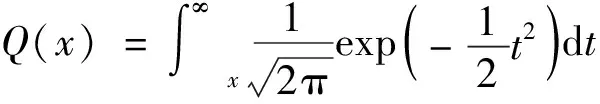
圖8為雷達不同發射功率下,3種方法生成的信號對應的信干噪比。在虛警率PFA=10-4時,根據式(11),可由圖8中數據得到如圖9所示的檢測概率。由圖9可知,CRWD-1D-CNN方法生成的信號對應的檢測概率隨雷達發射功率增加而增加,且要比MI方法信號對應的信干噪比平均高出10.40%,比SINR方法信號平均低6.43%。

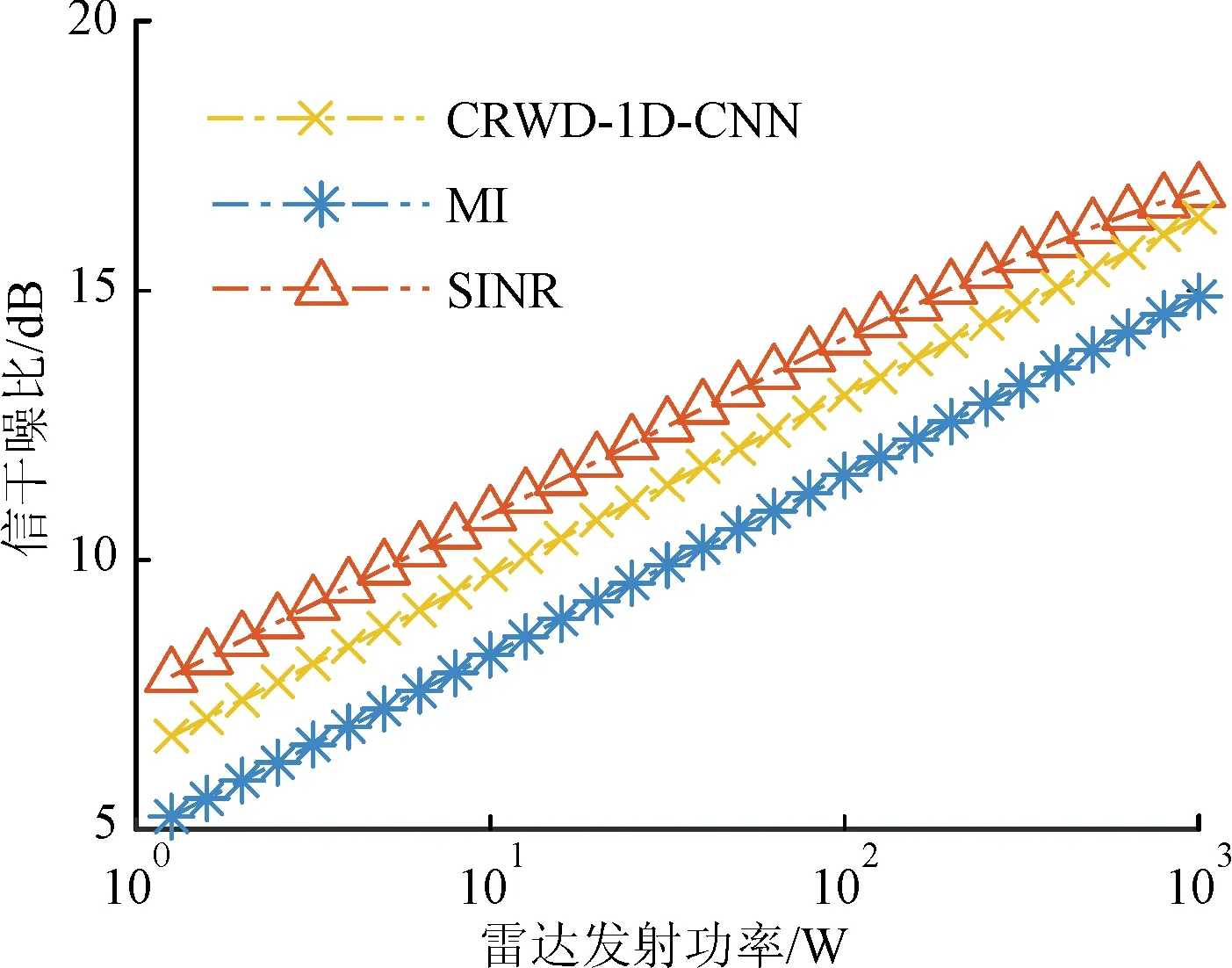
圖8 不同功率下3種方法生成的信號對應信干噪比

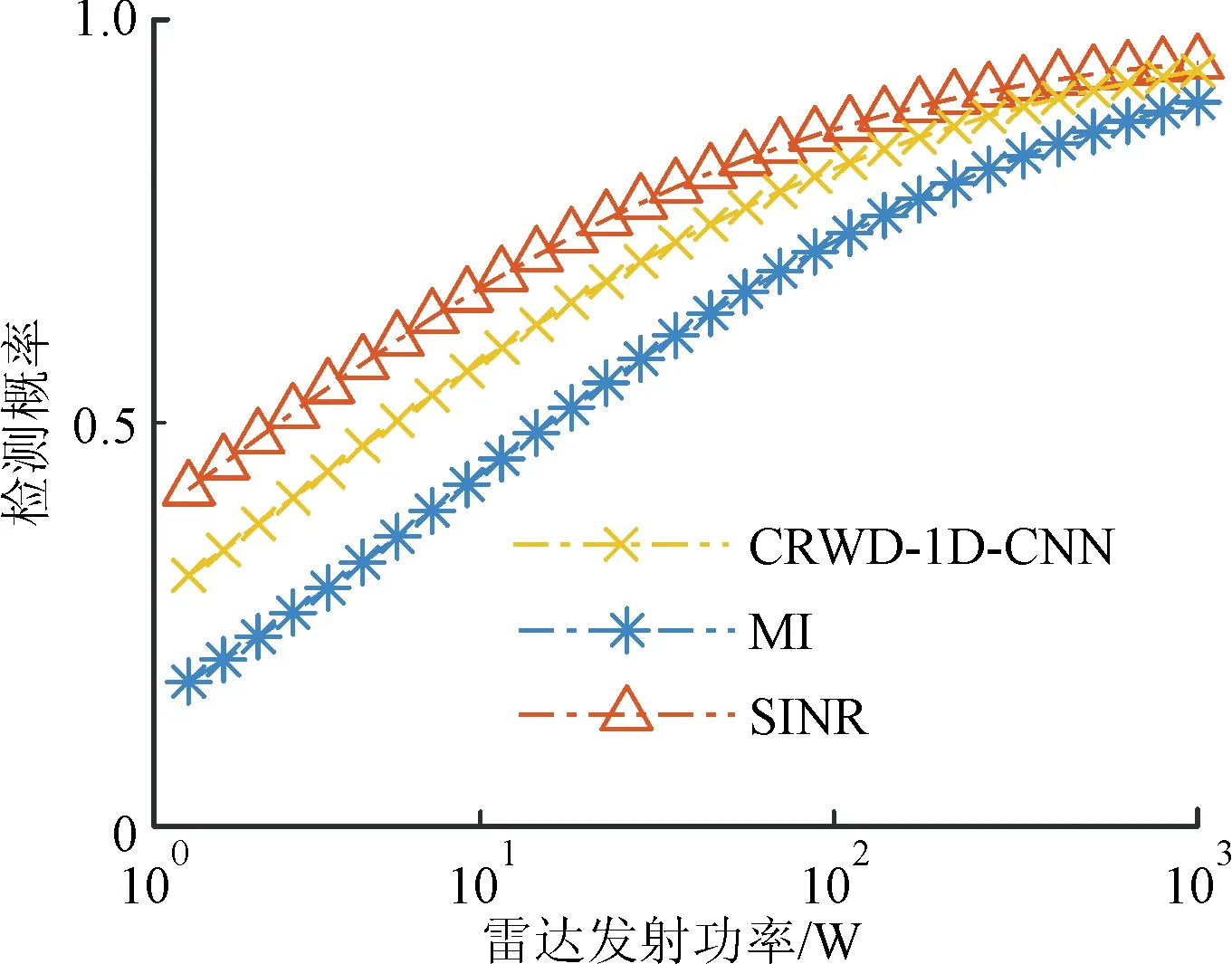
圖9 不同功率下3種方法生成的信號對應檢測概率

為衡量雷達綜合性能,本文提出一種目標最終識別率指標。定義

Pc=PdPr

(12)

式中:Pc為目標最終識別率,可作為衡量雷達綜合性能的指標;Pd為檢測概率;Pr為目標識別率。

Pr隨目標與回波之間的互信息量增加而增加,但兩者缺乏直接函數關系。本文提出一種用互信息量來衡量Pr的方法,定義

(13)

式中:Imx為雜波條件下發射信號為x(t)時,目標與回波之間的互信息量;Imxnc為不存在雜波時,目標與回波之間可獲得的最大互信息量。

表1為3種方法生成的信號對應平均檢測概率、平均識別概率和平均最終目標識別率。由表1可知,采用CRWD-1D-CNN方法生成的信號平均檢測概率和平均識別率均介于兩準則信號之間,即1D-CNN可在MI方法和SINR方法之間實現權衡,而CRWD-1D-CNN方法信號的目標最終識別率要比MI方法信號高0.64%,比SINR方法信號高2.13%,證明了CRWD-1D-CNN方法可聯合MI方法和SINR方法生成信號,提高雷達綜合性能。

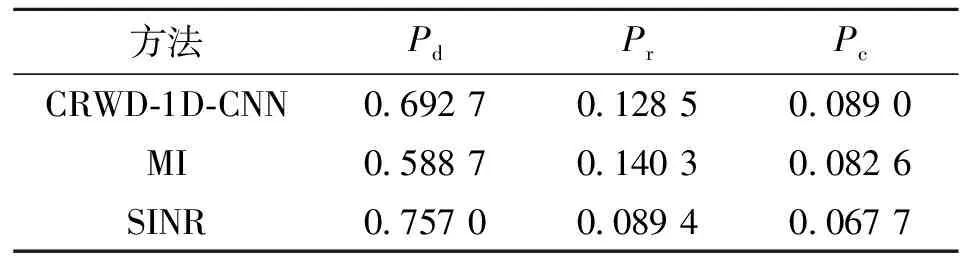
表1 3種方法生成信號對應的平均檢測概率、平均識別率和平均最終目標識別率

4 結 論

本文提出了一種雜波條件下使用1D-CNN的認知雷達波形設計方法CRWD-1D-CNN。利用1D-CNN對一維數據之間非線性關系的映射能力,實現了MI方法與SINR方法之間的聯合。為衡量雷達綜合性能,提出了一種新的最終目標識別率和利用互信息來衡量的目標識別率指標。實驗結果表明,當使用CRWD-1D-CNN方法所生成的波形作為發射信號時,與MI方法生成信號和SINR方法生成信號相比,雷達綜合性能指標均得到提升,證明了CRWD-1D-CNN方法所生成的波形可滿足雷達同時進行檢測和識別任務的需求,為聯合不同準則進行多任務雷達波形設計提供了一種新的解決方案。與波形設計領域許多文獻相同,本文僅得到了最優信號的能量譜分布,并沒有根據能量譜合成時域信號。根據給定的能量譜合成時域信號是信號處理領域的另一重要分支,是本文的后續研究方向。